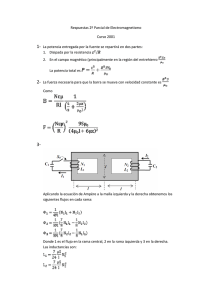
Sistema de unidades: SI Una espira cuadrada de alambre de lado

Sistema de unidades: SI
Una espira cuadrada de alambre de lado a lleva una corriente I.
a
I
Demostrar
p que el valor de B en el centro está dado por
2
2 0I b
~ =
B
k
a
Solución:
Dada una densidad de corriente, el campo magnético está dada como
R J~ (~r) (~r ~r)
~ (~r) = 0
B
dV
3
4 V
j~r ~rj
Que en el caso de una espira con corriente I se simpli…ca a
R d~l (~r ~r)
~ (~r) = 0 I
B
3
C
4
j~r ~rj
Considerando la espira sobre el plano del papel, el origen de coordenadas en
el centro de la espira y la corriente en el sentido contrario a las manecillas del
reloj, y si el punto de observación P (~r) es el centro de la espira, tenemos ~r = ~0,
así que
Ibi
( x; a=2; 0)
R a=2
B (centro) = 0 a=2 h
i3=2 dx+
4
2
x2 + (a=2)
+
+
+
0
4
0
4
0
4
R
R
a=2
a=2
a=2
a=2
R a=2
a=2
8
>
>
>
>
>
<
Ia
0
b
=
k
>
8
>
>
>
>
:
Ib
j
( a=2; y; 0)
h
i3=2 ( dy) +
2
2
y + (a=2)
Ibi
( x; a=2; 0)
h
i3=2 ( dx) +
2
x2 + (a=2)
Ib
j
(a=2; y; 0)
i3=2 dy =
2
y 2 + (a=2)
R a=2
R a=2
dy
dx
i3=2
h
i3=2
a=2 h
a=2
2
2
x2 + (a=2)
y 2 + (a=2)
R a=2
R a=2
dx
dy
h
i3=2 + a=2 h
i3=2
a=2
2
2
x2 + (a=2)
y 2 + (a=2)
h
1
9
>
>
>
>
>
=
>
>
>
>
>
;
=
0 Ia b
2
k
R a=2
a=2
h
d
2
2
+ (a=2)
p
p
Ia 4 2
2 2 0I b
= 0 b
k 2 =
k
2
a
a
Finalmente
p
2 2 0I b
~
B (centro) =
k
a
i3=2
2