análisis de la varianza (un factor)

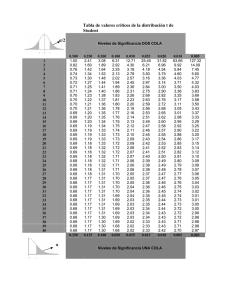
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 1
ANÁLISIS DE LA VARIANZA (UN FACTOR)
Notas de clase
Antonio Morillas
1
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 2
ÍNDICE
1. Introducción.
2. Modelo de un factor completamente aleatorizado.
3. Procedimientos para comparaciones múltiples.
4. Verificación de las hipótesis básicas.
5. Análisis de la varianza no paramétrico.
2
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 3
1. Introducción
El análisis de la varianza (ANOVA, de su expresión inglesa), debido a R.A. Fisher,
surge, poco después de la 1ª Guerra Mundial, como una técnica encaminada a comparar
las medias de más de dos poblaciones, que son observadas en circunstancias
experimentales no totalmente controlables u homogéneas. En concreto, inicialmente,
parte de los trabajos de este autor en investigación agraria y, por ello, ha incorporado
términos propios de esta campo en su desarrollo teórico: tratamiento, factor, unidad
experimental, etc. El problema que se plantea Fisher es cómo estudiar si existen o no
diferencias (en términos de media) en la respuesta o reacción que tienen un grupo de
unidades experimentales ante distintos tratamientos con un determinado factor. Por
ejemplo, ¿sería igual la cosecha de trigo (respuesta media), observada en diversos
grupos de parcelas (unidades experimentales), si se les somete a distintos niveles
(tratamientos) de abonado (factor)?. Si la respuesta es afirmativa y el experimento
estadístico ha sido diseñado correctamente, podría concluirse que el nivel de abonado
no afecta a la cosecha obtenida. Por el contrario, si hay diferencias significativas en la
cosecha media obtenida para cada nivel de abonado, podemos deducir que hay, al
menos, un nivel que determina que el volumen cosechado sea distinto de los demás
(supongamos que superior) y procederemos a la identificación del nivel que produce
esa mayor respuesta.
Su singularidad respecto al contraste de la diferencia de medias poblacionales
radica, además de que se emplea para comparar más de dos poblaciones, en que se
considera que los resultados pueden verse expuestos a efectos de factores no
controlables en el experimento: diferentes calidades de suelos, horas de insolación,
pendientes, etc., en el ejemplo anterior. Por eso, un objetivo básico del método es aislar
y evaluar la incidencia de los errores achacables al propio experimento. El ANOVA ha
tenido un gran desarrollo y ha dado lugar a una rama con personalidad propia en el
campo de la Estadística: el diseño de experimentos.
El análisis de la varianza también puede ser contemplado como un caso especial de
regresión (véase el Gráfico 1.1) en que la variable dependiente cuantitativa, Y, que se
asume es continua, viene explicada por una variable categórica (cualitativa o
3
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 4
cuantitativa, pero agrupada en clases, modalidades o categorías), X, que puede tomar k
categorías y que se supone, en principio, se encuentra siempre bajo control del
investigador, que decide tales categorías. La variable dependiente, Y, es la respuesta
(observación o medida) obtenida para las k categorías (tratamientos o niveles) de la
variable explicativa o factor, X, en cada una de las n unidades experimentales que
constituyen el tamaño (muestra) del experimento. En el gráfico mencionado, puede
observarse como la respuesta media de cada uno de los grupos de 5 unidades
experimentales observadas es diferente para cada nivel de factor, mostrando, en este
ejemplo, un mayor valor para el nivel o tratamiento C que para el A o el B.
Gráfico 1.1
Hablaremos de análisis de la varianza de un factor (one-way), cuando sólo se
contempla una sola variable explicativa. Al modelo de dos variables explicativas,
siempre observadas por categorías, le llamaremos análisis de la varianza de dos factores
(two-way), y así sucesivamente. En esta lección trataremos, exclusivamente, los
modelos de uno y dos factores.
El modelo más simple (véase Tabla 1) de diseño consiste en suponer que se tiene
sólo un factor y que las n unidades experimentales se asignan en forma completamente
aleatoria a cada uno de los k≥2 tratamientos (n= n1+ n2+...+ nj+... +nk). Los tamaños
muestrales de cada tratamiento no tienen por qué ser iguales. Las respuestas
individuales de cada una de las unidades experimentales serán llamadas yij .
4
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 5
El objetivo es comparar los efectos medios o respuestas medias, Y. j , que producen
los distintos tratamientos o niveles de factor. La hipótesis nula será que las medias
poblaciones son iguales, y, por tanto, igual a la media global, frente a la alternativa de
que al menos una no lo es:
H0: µ1=µ2=...=µj=...µk = µ
H1: no todas las µj son iguales
Por hipótesis, se supondrá normalidad y varianza igual en las poblaciones. Si se
acepta la hipótesis nula, por tanto, concluiremos diciendo que la respuesta es la misma
en todas las unidades experimentales y que no se ve afectada por los distintos niveles
de factor o tratamientos fijados1 por el investigador. Como es fácil de entender, el
contraste estadístico hará uso de las medias muestrales, y se basará, además de esta de
normalidad que acabamos de enunciar, en una serie de hipótesis que comentamos a
continuación.
Unidades
Experimentales (n)
Tratamientos
(Var. Explicativa, X)
Hipótesis Respuesta
(Var. Dependiente, Y)
Muestra:
Respuesta observada
Totales muestrales
Medias muestrales
Tabla 1: Análisis de la varianza
•••••
•••••••
••••••
......
• • • • • (n1) • • • • • • • (n2)
• • • • • • (nk)
X1
X2
Xk
......
Nivel 1
Nivel 2
Nivel k
Y1
Y2
Yk
......
N(µ1 , σ)
N(µ2 , σ)
N(µk , σ)
y12
y11
y1k
y21
y22
y2k
..
..
yi1
yi2
..
..
..
y n11
y n2 2
y nk k
T.1
Y.1
T.2
Y.2
......
......
......
..
yik
T.k
Y.k
La realización correcta de un diseño experimental de este tipo tiene su fundamento
en dos premisas fundamentales: aleatoriedad y repetición. La primera, en el proceso de
asignación de las unidades experimentales a los distintos tratamientos, garantiza la
imparcialidad y neutralidad ante la presencia de posibles efectos externos, no
controlables por el investigador, que puedan perturbar el experimento. La segunda,
mediante la observación de las unidades experimentales, que se supondrán homogéneas,
1
Sólo analizaremos aquí los modelos basados en esta premisa, llamados de efectos fijos. No se verá, por
tanto, el modelo bajo la hipótesis de efectos aleatorios, donde los tratamientos se eligen al azar.
5
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 6
sometidas a un mismo tratamiento, pondrá de manifiesto los cambios en la respuesta
que no son atribuibles a variaciones en los niveles de factor. Es decir, las variaciones
aleatorias o error experimental.
En estos conceptos se basan los dos diseños básicos de modelos para el análisis de la
varianza:
•
Diseño completamente aleatorio: todas las unidades experimentales son
homogéneas y su asignación a los distintos tratamientos (o viceversa) se hace de
forma totalmente aleatoria.
•
Diseño en bloques completamente aleatorio: no todas las unidades son
homogéneas, pero es posible agruparlas en bloques homogéneos y asignarles, en
cada uno de ellos, de forma totalmente aleatoria, los tratamientos
correspondientes. Se trata de limitar el error experimental, evitando, en la forma
mencionada, la heterogeneidad de las unidades experimentales en el análisis.
Antes de pasar a exponer algunos de los modelos más importantes, digamos que
la exigencia de que el investigador planee anticipadamente el experimento, hace que
esta metodología tenga pocas posibilidades de aplicarse con rigor a ciencias no
experimentales.
2. Modelo de un factor completamente aleatorizado
Se corresponde con el tipo de modelo formulado en el apartado anterior. Una sola
variable explicativa, o factor, con, al menos, dos categorías o niveles (tratamientos), que
producen una respuesta observable en las distintas unidades experimentales o elementos
muestrales. Se supone que estos son homogéneos y que se asignan en forma aleatoria a
los distintos tratamientos. Se trata, por tanto, de un diseño completamente aleatorizado.
El objetivo es comprobar si hay diferencias significativas en la repuesta media para
los distintos niveles de factor. Como dijimos, es una extensión del contraste de la
diferencia de medias de dos poblaciones normales, con varianzas desconocidas, pero
iguales. El objetivo, por tanto, es realizar el contraste siguiente:
H0: µ1=µ2=...=µj=...µk = µ
6
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 7
H1: no todas las µj son iguales
Si rechazamos la hipótesis nula, es que podremos distinguir los efectos que
producen los distintos tratamientos. Si la aceptásemos, cualquier discrepancia en las
respuestas medias sería achacable al azar, producto del error experimental.
La respuesta de la unidad experimental i ante el tratamiento j, yij , será igual a la
respuesta media del grupo de las nj unidades experimentales (homogéneas) sometidas a
este tratamiento, µj , más el error experimental o efecto aleatorio producido, εij . Puede
representarse mediante la siguiente ecuación:
yij = µj + εij
El efecto diferencial, τj , del tratamiento j respecto al efecto medio global o del
conjunto de la muestra, µ , puede escribirse como sigue:
τj = µj - µ
y el modelo quedaría expresado en los siguientes términos:
yij = µ + τj + εij ,
para
j=1, 2,...,k ; i=1, 2,..., nj
[1]
Se supone que los errores son independientes y se distribuyen normalmente, con media
cero y varianza constante:
εij ∼ N(0 , σ2)
para
j=1, 2,...,k ; i=1, 2,..., nj
Si trabajamos con la hipótesis de efectos fijos, es decir, si admitimos que los
niveles de factor son seleccionados a priori por el investigador, la distribución de la
respuesta será la misma que la del error (µ y τj serían constantes). Por tanto, se
distribuirá normal e independientemente, pero su media estará desplazada a µj (µ + τj =
µj):
7
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
yij ∼ N(µj , σ2)
para
p. 8
j=1, 2,...,k ; i=1, 2,..., nj
Las inferencias realizadas con este modelo sólo serán válidas para los niveles
que se han seleccionado previamente2. Esta hipótesis, junto con la de unidades
experimentales homogéneas, hace que se pueda considerar que se trabaja con la misma
población original, pero tratada en k formas diferentes.
Las hipótesis de normalidad e independencia de la respuesta, junto con la de
varianza constante, necesitan de una verificación previa a la aplicación del análisis. Se
ha comprobado que este resulta muy robusto ante la violación de la hipótesis de
normalidad, pero que, sin embargo, es muy sensible a la presencia de valores extremos
en las muestras (outliers). Por otro lado, si hay diferencias apreciables en las varianzas
de los distintos grupos, el test puede resultar afectado. Si, por ejemplo, existe asociación
entre los tamaños muestrales, nj , y las varianzas correspondientes, σ 2j , se ha
demostrado que el valor muestral del estadístico (veremos que es una F ) tiende a tomar
valores muy grandes y, por tanto, a rechazar la hipótesis nula, que, como se ha dicho, es
la de igualdad de medias o, de forma equivalente, que los efectos diferenciales son todos
nulos:
H0 : τ1 = τ2 = ...= τj =...= τk =0
El modelo dado por la ecuación [1], dado que τj = (µj - µ) y εij = (yij - µj ),
puede escribirse como sigue:
yij = µ + (µj - µ) + (yij - µj )
o, de otra forma,
(yij - µ) = (µj - µ) + (yij - µj )
[2]
Si observamos con detenimiento, esta ecuación nos está diciendo que la
diferencia respecto a la media global de cualquier observación, (yij - µ), se puede
descomponer en dos factores:
En el modelo de efectos aleatorios, se considera que τj ∼ N(0, σ2). Las inferencias serían válidas para
todo el conjunto de la población de niveles.
2
8
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
•
p. 9
La parte correspondiente a la diferencia inducida por el tratamiento, evaluada
por la diferencia de la media del grupo de unidades experimentales
sometidas a ese tratamiento a la media global del experimento: (µj - µ).
•
La diferencia observada en cada una las unidades experimentales sometidas
a ese mismo tratamiento respecto a la media dentro del mismo: (yij - µj ). Por
las hipótesis vertidas anteriormente (homogeneidad de las unidades
experimentales y aleatoriedad en su asignación), esta diferencia será de tipo
aleatorio, no explicada por el nivel de factor aplicado o tratamiento, y
recogerá el error experimental.
Si hubiera un tratamiento que produce resultados diferenciados, la diferencia
debida al mismo debería ser suficientemente mayor que la provocada por el error
aleatorio. Este será el razonamiento en que, como se verá más adelante, se apoyará el
test utilizado para la verificación de la hipótesis de medias iguales.
Como no será posible trabajar con los parámetros poblacionales µ y µj , habrá
que estimarlos a partir de las correspondientes medias muestrales, que, suponiendo σ2
igual para todos los grupos o niveles, son los mejores estimadores de las
correspondientes medias poblacionales. Les llamaremos, respectivamente, Y.. y Y. j .
Incorporando a la ecuación [2] estas estimaciones:
(yij - Y.. ) = (Y. j − Y.. ) + (yij - Y. j )
Elevando al cuadrado ambos miembros de la igualdad y sumando para i y para j,
tendremos:
nj
k
∑∑ ( y
j =1 i =1
k
nj
k
ij
nj
[
]
− Y.. ) =∑∑ (Y. j − Y.. ) + ( yij − Y.. ) =
2
2
j =1 i =1
k
nj
k
nj
= ∑∑ (Y. j − Y.. ) + ∑∑ ( yij − Y. j ) + 2∑∑ (Y. j − Y.. )( yij − Y. j )
j =1 i =1
2
j =1 i =1
2
j =1 i =1
Puede comprobarse que el último sumando de esta última expresión siempre será
nulo:
9
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 10
 nj

(Y. j − Y.. )( yij − Y. j ) = ∑ (Y. j − Y.. ) ∑ ( yij − Y. j ) = 0
∑∑
j =1 i =1
j =1
 i =1

k
nj
k
ya que la expresión entre corchetes es la suma de las diferencias respecto a su media de
los valores de las observaciones del grupo o tratamiento j. Por tanto, finalmente, queda:
k
nj
∑∑ ( y
j =1 i =1
ij
k
nj
k
nj
− Y.. ) = ∑∑ (Y. j − Y.. ) + ∑∑ ( yij − Y. j ) 2
2
j =1 i =1
2
[3]
j =1 i =1
Esta es la ecuación fundamental del análisis de la varianza. Nos dice que la suma
total de cuadrados (STC) de las desviaciones en la respuesta de las unidades
experimentales, con respecto a la media global del experimento, se descompone en dos
sumandos:
•
El primero, representa la suma de cuadrados de las desviaciones respecto a la
respuesta media global producidas por los distintos tratamientos (SCTR), en
términos de la diferencia de sus correspondientes respuestas medias respecto
a dicha media global. Es decir, la suma de cuadrados de las diferencias entre
grupos.
•
El segundo, recoge la suma de cuadrados de las desviaciones en la respuesta
de cada unidad experimental con respecto a la media obtenida dentro del
tratamiento (grupo, muestra) a que ha sido sometida. Es decir, la suma de
cuadrados de los errores experimentales (SCE) observados dentro de cada
grupo.
Así, pues, de la expresión STC = SCTR + SCE , puede concluirse que las
variaciones totales en la respuesta (STC) se explican por los efectos de las variaciones
inducidas por los distintos tratamientos (SCTR), más una componente residual que
recoge las variaciones debidas al error experimental (SCE).
Si las respuestas medias para los distintos tratamientos son iguales entre sí,
entonces SCTR=0, y todas las variaciones en la respuesta se deben, exclusivamente, al
error experimental (aleatorio). Para un valor grande de SCTR, mayor serán las
diferencias existentes entre las medias de los tratamientos y la global. Los distintos
niveles de factor (valores o modalidades de la variable explicativa), en tal caso,
explicarían, en principio, las variaciones en la respuesta (variable dependiente).
10
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 11
Si todas las respuestas son iguales dentro de todos y cada uno de los tratamientos
o grupos, entonces SCE=0. Absolutamente todas las variaciones en la respuesta se
deberían al efecto de los tratamientos.
Ambos sumandos, dada una suma total de cuadrados, juegan de forma inversa: a
un mayor valor de SCTR le corresponde un valor menor de SCE, y viceversa. Cuanto
mayor sea el primero respecto al segundo, tantas más razones habrá para rechazar la
hipótesis nula de que las respuestas medias son iguales. Por consiguiente, el cociente
SCTR/SCE , puede ser un estadístico adecuado para llevar a cabo el contraste de dicha
hipótesis3.
No es excesivamente complicado demostrar que
k
nj
k
k
SCTR
σ
2
=χ
2
k −1
. Veamos:
[
]
SCTR = ∑∑ (Y. j − Y.. ) 2 = n j ∑ (Y. j − Y.. ) 2 = ∑ n j (Y. j − µ ) − (Y.. − µ ) =
j =1 i =1
j =1
2
j =1
k
k
j =1
j =1
= ∑ n j (Y. j − µ ) 2 + n(Y.. − µ ) 2 − 2∑ n j (Y. j − µ )(Y.. − µ ) =
k
= ∑ n j (Y. j − µ ) 2 − n(Y.. − µ ) 2 , ya que
j =1
Por consiguiente,
SCTR
σ2
k
∑n
j =1
 Y −µ
= ∑ .j

j =1 σ / n j

k
j
(Y. j − µ )(Y.. − µ ) = n(Y.. − µ ) 2
2
  Y − µ 2
 −  ..
 , es una suma de los
  σ / n 

cuadrados de variables independiente y normalmente distribuidas4, con µ=0 y σ=1. Se
trata, por tanto, de una distribución Chi-cuadrado con k-1 grados de libertad.
Tampoco
k
nj
es
difícil
demostrar
SCE = ∑∑ ( yij − Y. j ) 2 , y se sabe que
j =1 i =1
que
SCE
σ
2
=χ
2
n−k
.
Se
ha
visto
que
n
j
1
1
SCE j , por lo
( yij − Y. j ) 2 =
sˆ j = n j − 1 ∑
nj −1
i =1
2
Se puede demostrar que E(SCTR/k-1)=σ2+(1/k-1)∑jnjτj2, que es mayor que E(SCE/n-k)=σ2. La región
crítica del test estará, por tanto, situada a la derecha de la distribución de este estadístico.
3
4
Las Y. j son medias muestrales provenientes de una distribución N(µ , σ2) y, por tanto, su distribución es
N(µ , σ2/nj).
11
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
que
k
2
j =1
j
∑ (n j −1)sˆ
p. 12
= SCE . Si dividimos por σ2 , teniendo en cuenta que las k muestras
son independientes, tendremos lo siguiente:
k
∑
(n j − 1) sˆ 2j
σ2
j =1
ya que
k
∑ (n
j =1
j
=
SCE
σ2
→χ
2
n−k
− 1) = n − k .
Se puede demostrar que SCTR y SCE son independientes, por lo que,
( SCTR / σ 2 ) / k − 1
( SCE / σ 2 ) / n − k
=
χ 2 / k −1
CMTR
→ 2k −1
→ Fk −1,n − k
CME
χ n −k / n − k
siendo, CMTR y CME los cuadrados medios de los tratamientos y los cuadrados medios
del error, respectivamente5. Así, pues, el test de la F de Snedecor será el adecuado para
contrastar la hipótesis de que las respuestas medias de los tratamientos son iguales,
frente a la alternativa de que al menos una no lo es:
H0: µ1=µ2=...=µj=...=µk=µ
H1: no todas las medias son iguales
Cuanto mayor sea la suma de cuadrados explicadas por los tratamientos, o
variación entre grupos, en relación a la explicada por los errores, o variaciones dentro de
los grupos, más evidente es que las respuestas medias a los diferentes tratamientos no
son iguales. Rechazaremos la hipótesis nula con valores suficientemente grandes de la F
observada, situándose la región crítica del test, por tanto, en la cola derecha de la
distribución F. La F observada vendrá dada por la siguiente expresión:
k
Fobs =
CMTR
=
CME
nj
∑∑ (Y
.j
− Y.. ) 2 / k − 1
ij
− Y. j ) 2 / n − k
j =1 i =1
nj
k
∑∑ ( y
j =1 i =1
Pueden obtenerse fórmulas de cálculo más sencillas para las diferentes sumas de
cuadrados que intervienen en el análisis, desarrollando convenientemente las
Obsérvese que SCTR estima σ2 , a través de la distribución de las medias, [k. (σ2/k)= σ2], mientras que
SCE hace lo mismo en la distribución de las respuestas. La distribución muestral de un ratio de este tipo
es una distribución F central, si la hipótesis nula de igualdad es cierta. La hipótesis alternativa es que esta
F no es central sino tumbada hacia la derecha (parámetro de no centralidad,
τ 2j , significativamente
5
∑
distinto de cero), que es, precisamente, el contraste ya visto anteriormente.
12
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 13
expresiones iniciales. Dejamos su obtención como ejercicio para el alumno, que debe
obtener las siguientes expresiones finales:
nj
k
k
k
T. 2j
j =1
nj
SCTR = ∑ ∑ (Y. j − Y.. ) = ∑ n Y − nY.. = ∑
2
j =1 i =1
nj
k
2
j .j
j =1
nj
k
2
k
−
nj
T..2
n
STC = ∑∑ ( y ij − Y.. ) = ∑∑ y − nY.. = ∑∑ y ij2 −
2
j =1 i =1
j =1 i =1
2
ij
2
j =1 i =1
T..2
n
SCE = STC − SCTR
Es usual presentar los resultados obtenidos en forma de una tabla, cuyo
contenido es el siguiente:
Fuente de
variación
Grados de
libertad
Tabla ANOVA
Suma de
cuadrados
k
-Tratamientos
(Entre grupos)
k-1
-Error
(Dentro grupos)
n-k
∑∑ (Y
j =1 i =1
k
n-1
.j
nj
∑∑ ( y
− Y.. ) 2
j =1 i =1
Fobs =
− Y. j ) 2
ij
− Y.. ) 2 ⇒ η2 =R2=(SCTR/STC)
nj
∑∑ ( y
SCTR/k-1
F observada
ij
j =1 i =1
k
Total
nj
Cuadrados
medios
CMTR
CME
SCE/n-k
El sígnificado de η2 (eta cuadrado) es similar al de R2 en el análisis de regresión,
ya que da el porcentaje de variabilidad en la respuesta que viene explicado por el factor
o variable explicativa. Finamente, como se pone de manifiesto en la nota a pié de página
número 3, hay que señalar que los cuadrados medios del error (SCE/n-k), es el mejor
estimador de la varianza poblacional (σ2).
3. Procedimientos para comparaciones múltiples.
Si la hipótesis nula, de igualdad de medias, resulta rechazada, la cuestión inmediata
que surge es como localizar cuáles son los grupos o tratamientos que tienen medias
diferentes. Es necesario, por tanto, realizar un análisis ex post, con objeto de encontrar
la media o medias que resultan ser diferentes y por las que la hipótesis nula es
rechazada.
13
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 14
Hay diversas propuestas para llevar a cabo este procedimiento de comparación
entre múltiples medias: Mínima Diferencia Significativa (LSD, en inglés), Bonferroni,
Tukey, Scheffé, Duncan, ...). El primero no garantiza el mantenimiento del nivel de
significación para el conjunto del experimento. Los demás son soluciones de
compromiso entre el cumplimiento de esta garantía y la pérdida de potencia del test que
generalmente supone su aplicación. Vamos a ver, a continuación, el procedimiento de la
Mínima Diferencia Significativa (MDS), propuesto por Fisher.
Sean Y. j e Y.l , respectivamente, las medias muestrales de los grupos o tratamientos
j y l . Su diferencia será un estadístico muestral cuya distribución, como ya conocemos,
será la siguiente:
(Y. j − Y.l ) − ( µ j − µ l )
σ (Y
≈ N (0,1)
. j −Y. l )
dónde,
σ (Y
. j −Y. l )
= σ
2
Y. j
+σ
2
Y. l
=
σ Y2
.j
nj
+
σ Y2
.l
nl
=σ
1
1
+
n j nl
suponiendo que se cumple la hipótesis, formulada anteriormente, de que la respuesta se
distribuye normalmente con media µ y varianza σ2 , constante e igual en todos los
grupos o tratamientos (homoscedasticidad).
Como σ2 es desconocida, la estimaremos mediante los cuadrados medios de los
errores o error cuadrático medio, que se demuestra es su mejor estimador insesgado. Es
decir, sˆ 2 =
SCE
. Por lo tanto, según se sabe,
n−k
(Y. j − Y.l ) − ( µ j − µ l )
1
1
sˆ
+
n j nl
≈ t n −k
Mediante este estadístico, se puede establecer un intervalo de confianza del
100(1-α)% para cualquiera diferencia de medias:
14
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 15

1
1
+ 
(Y. j − Y. j ) ± t n −k ,α / 2 . sˆ
n j nl 

Si el intervalo contiene el valor cero, la diferencia de medias no será
significativa.
Es posible plantear este procedimiento de otra forma. Supongamos que H0 es
cierta (por tanto, µj = µl ), y sea tn-k,α/2 el valor del estadístico correspondiente al punto
crítico del test, con un nivel de significación α. Se puede afirmar que en este punto,
según la fórmula que expresa la distribución de tn-k, la diferencia de medias viene dada
por la siguiente ecuación:
Y. j − Y.l = t n −k ,α / 2 . sˆ
1
1
+
n j nl
Puesto que α, nj y nl son constantes, punto crítico del test y diferencia de medias
se determinan mutuamente, pudiendo afirmarse que esta es la discrepancia máxima
permitida en cualquier pareja de medias para no considerarlas como diferentes, dado un
nivel de significación α para realizar el contraste. Así, pues, puede afirmarse que la
diferencia mínima (MDS) a partir de la cual estamos dispuestos a rechazar la igualdad
entre las dos medias consideradas, viene dada por la expresión:
MDS = t n −k ,α / 2 . sˆ
1
1
+
n j nl
Cualquier valor superior nos llevaría a rechazar la hipótesis de igualdad de las
dos medias sometidas a comparación. Esta expresión también puede ser escrita en la
forma que sigue:
 1
 1
1
1
MDS = 
+  . sˆ 2 . t n2− k ;α / 2 = 
+  . CME . F1, n − k ;α
n

n

 j nl 
 j nl 
Es preciso obtener el valor de esta expresión para cada una de las k(k-1)/2
comparaciones repetidas de medias que son necesarias realizar, lo que en la práctica
supone repetir ese número de veces el contraste de la t que ya se viera en capítulos
anteriores.
15
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 16
Sin embargo, hay un caso especial en que es posible simplificar todo este
procedimiento. Si se trata de un diseño experimental equilibrado (igual número de
observaciones o unidades experimentales en cada grupo o tratamiento), entonces resulta
que nj = nl = m , la igualdad anterior quedaría como sigue:
MDS = t n −k ;α / 2 . sˆ
2
m
=
2
. CME . F1,n − k ;α
m
En tal caso, los cálculos se simplifican bastante, ya que el valor obtenido para la
MDS, con el nivel de significación dado para obtener el valor de la F, sirve como única
referencia para contrastar todas las diferencias de medias. El intervalo de confianza
único sería el siguiente:
(Y. j − Y.l ) ± MDS
Si el valor cero está dentro del intervalo formado, aceptaremos la hipótesis nula,
de igualdad de medias. En caso contrario, la rechazaremos. Visto de otra forma, sólo si
Y. j − Y.l ≤ MDS aceptaremos H0. Es evidente que, en este caso, los cálculos se
simplificarían enormemente. El procedimiento lógico es, en primer lugar, ordenar las
medias, de menor a mayor valor. A continuación, se comienzan las comparaciones por
las dos medias más alejadas entre sí, continuando con este criterio hasta que se
encuentre una diferencia no significativa. En este momento puede ahorrarse el esfuerzo
de continuar con los contrastes, puesto que no será posible encontrar ninguna pareja de
medias que sea diferente, al ser su diferencia siempre menor que la primera hallada
como no significativa.
Sin embargo, este método de la MDS tiene un inconveniente. Obsérvese que si
el error de Tipo I en el contraste se estableciera como α=0,05 y hubiera k grupos, el
número esperado de diferencias que resultarían significativas, a pesar de que la hipótesis
nula de igualdad fuese cierta, sería 0,05[k(k-1)/2], ya que α es la probabilidad de
rechazar la hipótesis nula siendo cierta y [k(k-1)/2] el número total de comparaciones
que se pueden realizar. Bastaría con que k tomase un valor suficientemente grande para
que se pudiesen extraer falsas conclusiones, encontrándose excesivas parejas con
diferencias significativas. Ello se debe a que el error de Tipo I en los sucesivos
16
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 17
contrastes con el estadístico t, es el error de cada comparación en particular, pero no es
el error para el conjunto del experimento. Por ejemplo, si tuviéramos cinco tratamientos,
suponiendo que α=0,05, la probabilidad de rechazar la hipótesis nula en una
comparación específica, siendo falsa, sería (1-α)=0,95. Si suponemos que los tests son
independientes, tal probabilidad para el conjunto del experimento (10 comparaciones)
vendría dada por (0,95)10=0,60. El verdadero valor global de α, para todas las
comparaciones, sería de 0,4 y no el 0,05 requerido. Su autor recomienda, por tanto, que
sólo se aplique si se rechaza la hipótesis nula, de igualdad de medias, con el test F, para
un nivel α de significación (test de la MDS “protegido”). En estas circunstancias se ha
demostrado que es un test bastante efectivo.
Se han aportado procedimientos alternativos que intentan reducir el error de
Tipo I para el conjunto del experimento y generalizar la posibilidad de comparaciones
entre subconjuntos de medias. Los de Bonferroni, Scheffé y Tukey, quizás sean los más
conocidos y vienen incorporados en la mayoría de los paquetes estadísticos para
ordenador personal. Cada uno debería aplicarse en el caso para el que está más indicado,
careciendo de sentido la aplicación indiscriminada y simultánea de todos ellos. A
continuación, vamos a definir los tests propuestos por estos autores.
Aproximación de Bonferroni:
Se puede demostrar que si α es el nivel de significación propugnado para todo
el experimento y α* el correspondiente a cada contraste entre dos medias particulares, se
cumple que α≤α*[k(k-1)/2]. Con base en esta desigualdad, Bonferroni propone que para
cada una de las comparaciones se tome el nivel de significación dado por
α* = α /[k(k-1)/2]
Por tanto, para un nivel global de significación α, el intervalo de confianza para
la igualdad de dos medias se definiría como sigue:
(Y. j − Y.l ) ± t n −k ,α * / 2 . sˆ
1
1
+
n j nl
Si el número de comparaciones ([k(k-1)/2]) es relativamente grande, para un
valor de α dado, lo normal es que α* sea muy pequeño. Por lo tanto, rechazar la
igualdad de las dos medias se hace bastante más difícil que en las comparaciones
17
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 18
individuales del método anterior (MDS). Suele aconsejarse utilizar este test de
Bonferroni cuando el número de comparaciones no es muy elevado, dejando para estos
casos otros procedimientos como el de Scheffé, por ejemplo.
Aproximación de Scheffé:
Es el procedimiento más conservador para contrastar si las diferencias de medias
son significativas y persigue que el error de Tipo I para el experimento en su conjunto
sea α en todos los posibles contrastes que se puedan realizar entre las medias, no sólo
por parejas, sino, también, entre subconjuntos de medias. En este sentido es el más
flexible, aunque está más indicado para contrastes planificados (diseñados ex ante por el
investigador). El intervalo de confianza que propone para ello viene dado por la
siguiente expresión:
1
1
(Y. j − Y.l ) ± sˆ. ( k − 1). Fk −1,n −k ;α . + 
 n j nl 
Obsérvese el parecido de esta expresión con la formulada para la MDS, cuando
se utiliza el estadístico F en los cálculos. En este caso, aparece con los grados de
libertad de SCTR, k-1, y viene multiplicada por este mismo valor.
Aproximación de Tukey:
Esta alternativa utiliza para las comparaciones entre medias la distribución de
rangos studentizada y, en principio, supone que el experimento es equilibrado, lo que es
una restricción para su aplicación generalizada6; es decir, que los tamaños de las k
muestras son iguales (m). El rango studentizado se define como la distribución muestral
del rango de la muestra dividido por la desviación éstándar estimada. Si sˆ 2 = CME y el
rango se basa en las medias de muestras de tamaño m, este estadístico se define como
sigue:
q=
(Ymax − Ymin )
sˆ 2 m
6
Hay quien sostiene que, para tamaños muestrales no muy distintos, este test es muy robusto y es posible
su utilización. En tal caso, hay que hacer m=n/k , siendo n el tamaño del experimento.
18
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 19
Si se toma un valor crítico de esta distribución para una comparación entre
parejas de medias, obtendríamos el nivel de significación apropiado para el peor de los
casos posibles de diferencias entre medias. Por tanto, parece razonable aceptar que tal
nivel sería el adecuado para todas las comparaciones posibles entre medias, es decir,
para el conjunto del experimento. La distribución de este estadístico depende del
número de medias (k), de los grados de libertad del error cuadrático medio (gl=n-k) y
del nivel de significación (α). Conocido el valor crítico, qα(k,gl), se puede calcular el
estadístico llamado W de Tukey o, también, “diferencia honestamente significativa”,
como sigue:
W = qα ( k , gl ) CME m
Tomando este valor como referencia, cualquier pareja de medias cuya diferencia
sea mayor al mismo se aceptará como significativamente diferentes.
19
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 20
4. Verificación de las hipótesis básicas.
Se ha visto como la comparación de las múltiples medias en el análisis de la
varianza concluye con un test, basado en la distribución F de Snedecor. La validez de
este test, sin embargo, depende del cumplimiento de las hipótesis básicas que se han
formulado sobre el modelo. Así, la violación de la hipótesis de normalidad y/o
independencia en la respuesta y en los errores echaría por tierra la distribución Chicuadrado que se obtuvo para las sumas de cuadrados, y, por tanto, el test F realizado
finalmente. La existencia de heteroscedasticidad (varianzas distintas en los tratamientos)
puede hacer que el valor de las sumas de cuadrados no se deba exclusivamente a los
distintos niveles de factor. Si la asignación de las unidades experimentales no se hace al
azar, puede que los errores no se distribuyan en forma aleatoria, etc.
Hay un enfoque sencillo, gráfico, para estudiar el cumplimiento de estas
hipótesis, que es observar el comportamiento de los errores. De cualquier forma, es
posible aplicar cualquiera de los test de normalidad y aleatoriedad, ya estudiados en el
contexto de los contrastes no paramétricos. Veamos algunas propuestas simples,
incorporadas en la mayoría de los paquetes estadísticos.
a) Normalidad.
Como se acaba de comentar, una alternativa válida sería hacer el contraste de
Kolmogorov-Smirnov-Lilliefors. Otra vía de análisis es la utilización del análisis
exploratorio de datos, utilizando instrumentos tales como los diagramas de barras,
gráficos de tallos y hojas (stem and leaf), para observar la forma de una distribución, o
los de cajas (box-and-wisker), que suelen ser bastante útiles para detectar valores
extraños. Estos análisis es conveniente realizarlos mediante la distribución de los errores
o residuos (yij - Yi. ), ya que, al ser yij=µ+τj+εij, los valores observados en la respuesta
tendrán las características de las distribución de (τj+εij) y sólo la distribución de los
residuos (estimación de los errores) nos podrá informar sobre el cumplimiento o no de
las hipótesis básicas del modelo formulado.
20
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 21
Se suelen utilizar, también, los llamados diagramas o gráficos Q-Q (cuantilcuantil), en los que, en general, los cuantiles de una muestra se representan en relación a
sus valores esperados en una distribución
3.5
RESIDUOS ESPERADOS
2.5
normal. Este gráfico debería dar lugar a una
1.5
línea recta y estar comprendidos en el
0.5
-0.5
intervalo (-3,+3), si los datos proceden de
-1.5
-2.5
-3.5
-3.5
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
RESIDUOS OBSERVADOS
3.5
residuos
RESIDUOS ESPERADOS
2.5
observados,
previamente
estandarizados (εij / (CME)1/2), se colocan en
1.5
0.5
-0.5
el eje de abscisas y los esperados, según la
-1.5
distribución normal tipificada, se toman en el
-2.5
-3.5
-3.5
una población distribuida normalmente. Los
-2.5
-1.5
-0.5
0.5
1.5
2.5
RESIDUOS OBSERVADOS
Figura 4.1
3.5
eje de ordenadas. Una nube de puntos
próxima a una línea recta, hará plausible la
hipótesis de normalidad en los residuos y, por tanto, en la respuesta. Por el contrario,
cualquier desviación de esta pauta de comportamiento indicará una desviación de la
hipótesis de normalidad. Además, valores muy alejados del recorrido propio de una
normal tipificada, (-3,+3), pueden indicar la presencia de valores extremos en la muestra
(outliers), también detectables, como se ha dicho anteriormente, mediante los gráficos
de cajas (box-and-whisker plots). La figura 4.1 recoge dos casos de análisis de residuos.
En el primero de ellos, la hipótesis de normalidad es aceptable; en el segundo, además
del comportamiento no aleatorio de los residuos, su alejamiento de la recta, indicaría
una desviación de la normalidad.
El test F es muy robusto ante la violación de la hipótesis de normalidad. Los
efectos, por tanto, del incumplimiento de esta hipótesis no suelen ser, en general,
importantes. Tales efectos se manifiestan, especialmente, ante una desviación fuerte en
la asimetría de la distribución o la existencia de valores extremos. Claro que, en tales
casos, las medias no deberían de ser utilizadas como valores representativos de la
tendencia central en la población y carecería de interés hacer inferencias sobre ellas.
Por otro lado, si el tamaño muestral de los tratamientos es suficientemente
grande, siempre se puede aplicar el teorema central del límite a la distribución muestral
de la media, que, como se sabe, se distribuirá normalmente, aunque la población de
origen no sea normal. En cualquier caso, pueden intentarse transformaciones de los
21
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 22
datos que conduzcan a la normalidad o, finalmente, acudir al análisis de la varianza no
paramétrico, mediante el test de Kruskal-Wallis, basado en la comparación múltiple de
las medianas, que veremos más adelante.
b)Homoscedasticidad (igualdad de varianzas).
Si las varianzas de los grupos no son iguales, las sumas de cuadrados obtenidas
podrían tomar valores distintos sólo porque la variabilidad respecto a la media
(varianza) en cada grupo es diferente y no porque los niveles medios de factor difieran
de uno a otro grupo o tratamiento. En este caso, no todas las poblaciones tendrán la
misma varianza y no se debería usar la varianza del conjunto del experimento como una
estimación del correspondiente parámetro poblacional, que se supone igual pata todas
ellas. En consecuencia, el test F (cociente entre dos estimadores de varianzas que se
suponen iguales) deja de ser válido.
Hay que decir que aquí, también, el
DESVIACIONES ESTANDAR
test F se comporta en forma robusta,
especialmente si los tamaños de las
muestras son similares, siendo, como
máximo, la mayor el doble de la menor (la
MEDIAS
(r=0,96)
distribución muestral de las varianzas,
especialmente para muestras pequeñas, es
DESVIACIONES ESTANDAR
muy dispersa, por lo que importantes
diferencias muestrales en las varianzas
pueden
no
ser
estadísticamente
significativas). Los problemas graves se
producen cuando hay una relación entre
MEDIAS
(r=0,05)
medias y varianzas.
Figura 4.2
Una forma sencilla de detectar
posibles problemas de este tipo es mediante el gráfico desviación típica-media (véase la
figura 4.2), que pone en evidencia la posible existencia de correlación entre las
varianzas y las medias de los tratamientos. Otros procedimientos aplicables son la
22
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 23
comparación de la dispersión de los residuos por tratamientos, mediante los
correspondientes gráficos de cajas o, si las muestras son muy pequeñas y lo anterior no
es significativo, la representación de la secuencia de los mismos que, en caso de
violación de esta hipótesis de homoscedasticidad, suele dar una distribución asimétrica.
De existir, puede afirmarse que es muy negativo para la fiabilidad del test F, puesto que
tiende a inflar el nivel de significación, rechazando la igualdad de medias. Por ejemplo,
puede ocurrir que la única media diferente a las demás, la mayor de todas, sea la
procedente de la muestra que, también, presenta mayor varianza. El test F podría dar
como significativa la diferencia de esta media, mientras que un test t en esa muestra
sobre el valor poblacional de la media, proponiendo como tal en la hipótesis nula alguna
de las observadas en los otros grupos, no arrojaría diferencias estadísticamente
significativas, dada la gran variabilidad que existe en el mismo y el consiguiente reflejo
que este hecho tendría en el tamaño del intervalo de confianza obtenido.
Este hecho suele ocurrir cuando hay valores extremos (outliers) en los datos.
Basta con que existan uno o dos valores de este tipo en una muestra con pocas
observaciones, para que se eleve fuertemente la media y, también, la varianza. Ello
conduciría a detectar, inadecuadamente, una media diferente a las demás y un valor
observado de la F superior a lo normal, provocado por la gran varianza (cuadrados
medios) de esta muestra o tratamiento. Sin embargo, eliminando los valores extraños, la
hipótesis nula de igualdad de medias sería, probablemente, aceptada.
En cualquier caso, si se piensa que se puede estar en presencia de varianzas
distintas, es recomendable realizar un test de hipótesis para verificarla. Hay diferentes
test para contrastar la hipótesis de igualdad de varianzas: Cochran, Bartlett-Box,
Hartley, entre otros. Todos ellos descansan en la hipótesis de normalidad. Uno de los
más utilizados es este último, llamado Fmax de Hartley, que será el que veremos a
continuación.
Se basa, el test de Hartley, en el cociente entre la mayor y la menor de la
varianzas muestrales. Bajo la hipótesis nula, de que las varianzas son iguales, este autor
obtuvo los valores críticos del test, en función del número de varianzas incluídas en el
test, k, y de n − 1 , siendo n el tamaño muestral medio de los tratamientos o muestras (si
no es entero se tomará sólo la parte entera):
23
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
H=
p. 24
sˆmax
→ Fmax;k ,n −1
sˆmin
Cuanto mayor sea este cociente, mayor será la posibilidad de rechazar la
hipótesis de igualdad de varianzas. Los valores críticos del test están tabulados. Como
se acaba de decir, el cumplimiento de la hipótesis de normalidad es una exigencia para
la utilización del test. En caso de incumplimiento, debe aplicarse otro procedimiento.
El estadístico C de Cochran es muy similar al anterior y, también, está tabulado.
Su definición es la siguiente:
C=
2
sˆmax
k
∑ sˆ
2
j
j =1
Por último, el estadístico B de Bartlett, de complicada expresión que no
reproducimos, sigue una distribución χ k2−1 . Una ulterior transformación posibilita una
aproximación (Bartlett-Box) a una distribución F.
Los tres contrastes suelen venir en los programas estadísticos más conocidos,
por lo que basta observar el nivel de significación (p-value) obtenido y, con esta
información, tomar la decisión de aceptar o rechazar la hipótesis nula, que en todos los
casos es la de igualdad de las varianzas.
Si las diferencias entre varianzas son producidas por la existencia de algún tipo
de relación entre la respuesta y alguna característica de las unidades experimentales (por
ejemplo, magnitudes económicas que varían en porcentajes, mayor variabilidad de la
longitud de una planta grande que de una pequeña, etc.), es muy posible la relación
entre la desviación estándar y la respuesta media. En este caso, puede ser útil recurrir a
transformar los valores de las observaciones, intentando que cumplan las hipótesis
básicas. En este sentido, se pueden realizar algunas transformaciones que tiendan a
equilibrar las varianzas. Por ejemplo, si la media es proporcional a σ, el modelo
logarítmico sobre las yij evitaría el problema. Si la proporción fuese respecto a σ2, se
debería tomar la raíz cuadrada de yij . En caso de datos expresados en proporciones o
porcentajes, se aconseja tomar arcsen( y ij ). Estas transformaciones suelen venir
incluidas en las opciones de algunos paquetes estadísticos.
24
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 25
c) Independencia.
Otra hipótesis básica que se debería contrastar, porque, como las anteriores,
puede afectar al test F utilizado en la
0.25
tabla ANOVA, es si las muestras
RESIDUOS
0.15
tomadas
0.05
para
cada
de
tratamientos
son
-0.05
observaciones
-0.15
aleatorias. Si esta hipótesis no se cumple,
-0.25
0
1
2
3
4
5
6
7
8
9
10
11
12
OBSERVACIÓN
no
es
posible
o
grupo
garantizar
que
las
respuestas, yij , sean independientes.
3.5
2.5
RESIDUOS
1.5
Cualquiera de los tests estudiados
0.5
en otras lecciones (test de rachas, por
-0.5
-1.5
ejemplo) para detectar la aleatoriedad,
-2.5
-3.5
0
1
2
3
4
5
6
7
8
9
10
11
12
sería
de
aplicación
a
este
fin.
OBSERVACIÓN
Figura 4.3
Generalmente, se utilizan los residuos
para llevarlos a cabo. El empleo de
gráficos de residuos, de nuevo, puede ser útil para detectar un posible comportamiento
no aleatorio de los mismos y, por tanto, de la respuesta: si se distribuyen de forma
aleatoria, sin sistemática alguna, a lo largo del eje de abscisas, y su media es
aproximadamente cero, podremos deducir que existe independencia. Sin embargo, un
comportamiento según cierto modelo, deducible de la visión del gráfico, debe hacernos
pensar en la posibilidad de un comportamiento no aleatorio en la respuesta (véase la
figura 4.3).
25
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 26
5. Análisis de la varianza no paramétrico.
Cuando la hipótesis de normalidad no se cumple, pero se supone que los k≥2
tratamientos tienen la misma distribución, existe la posibilidad de verificar si hay una
respuesta diferenciada ante los tratamientos, utilizando un test no paramétrico de
localización para k muestras aleatorias independientes. Los niveles de respuesta se
miden, ahora, mediante las correspondientes medianas. Para el diseño de un factor
completamente aleatorizado suele utilizarse el test de Kruskal-Wallis, mientras que para
el modelo en bloques el test más generalizado es el de Friedman.
Test de Kruskal-Wallis
El test de Kruskal-Wallis es un test no paramétrico que se utiliza para comparar
tres o más muestras. La hipótesis a contrastar es que todas las poblaciones tienen la
misma función de distribución, frente a la alternativa de que al menos dos difieren en su
localización (mediana). Es un test análogo al utilizado en el análisis de la varianza
(ANOVA) para un diseño completamente aleatorizado, por lo que puede considerarse
un ANOVA no paramétrico, pero que no depende, como aquel, de la hipótesis de que
todas las poblaciones que se someten a comparación se distribuyen normalmente. Sólo
se supondrá que las poblaciones tienen la misma distribución. Se puede considerar
como una extensión lógica del test de Wilcoxon-Mann-Whitney al caso de más de dos
(k) poblaciones, pudiéndose obtener dicho test a partir de este de Kruskal-Wallis sin
más que particularizar para k=2.
Su finalidad, como acabamos de decir, es la verificación de la igualdad de las
medianas, M, de los k grupos o tratamientos. La hipótesis a contrastar es, por lo tanto,
H0 : M1= M2=...= Mk
H1 : no todas son iguales
El desarrollo del test es relativamente fácil y exige menos cálculos que los
necesarios para completar una tabla ANOVA. Los pasos a seguir para la aplicación del
test son los siguientes:
26
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 27
Test de Kruskal-Wallis
Muestras (Tratamientos)
1
2
..
k
y11(r11)
y12(r12)
..
y1k(r1k)
y21(r21)
y22(r22)
..
y2k(r2k)
..
..
..
..
y n11 ( rn11 )
y n2 2 ( rn2 2 )
..
y nk k ( rnk k )
Suma rangos
R.1
R.2
..
R.k
Medias rangos
R.1
R.2
k
nj
j =1
i =1 j =1
R.k
k
R.. = ∑ R. j = ∑∑ rij = 1 + 2 + ... + n = n(n + 1) 2
1.- De ser cierta la hipótesis nula, puede afirmarse que las distintas muestras provienen
todas
de
una
misma
población.
Por
tanto,
podemos
considerar
las
k
n = ∑ n j observaciones del experimento como elementos de una muestra única que
j =1
ordenaremos de menor a mayor.
2.- Se asigna el correspondiente rango, rij , a cada una de las observaciones, yij. De
existir valores iguales, se sigue el mismo criterio que en el test no paramétrico de
Wilcoxon, visto en otra lección: asignarle a todos ellos la media de los valores de sus
respectivos rangos.
3.- Se calcula para cada muestra (tratamiento) la suma de los rangos, R.j .
4.- Se obtiene el valor del estadístico de Kruskal-Wallis, que se define como sigue7:
1
H= 2
s
 k R.2j n(n + 1) 2 
−
∑
 , con
4
 j =1 n j

s2 =
n
1  j k 2 n(n + 1) 2 
∑∑ rij −

n − 1  i =1 j =1
4

7
El test aplica las fórmulas usuales del ANOVA a los rangos, que sustituyen a las observaciones en los
cálculos. Esto hace que se simplifiquen algo las expresiones de los correspondientes cuadrados medios.
Sin embargo, el test estadístico es diferente a la F usual, ya que se basa en el cociente entre SCTR y STC.
27
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 28
Si no se repite ningún valor en las muestras (mismo rango), esta expresión se
convierte en otra de más simple manejo8:
2
k R
12
H=
∑ . j − 3(n + 1)
n( n + 1) j =1 n j
De este estadístico existen tablas que dan los valores críticos, para los tamaños
ordenados de las k muestras y para diferentes niveles de significación. Además, puede
demostrarse que para nj > 5, si la hipótesis nula es cierta, puede aproximarse una
distribución Chi-cuadrado con k-1 grados de libertad. La cola de la derecha puede ser
utilizada como región crítica del contraste.
k
Conceptualmente, el test parte del estadístico V = ∑ n j ( R. j − R.. ) 2 , que viene a
j =1
ser algo similar, formalmente, a la suma de cuadrados de los tratamientos, utilizando los
valores de los rangos en vez de las respuestas observadas, y, por tanto, R . j y R .. son,
respectivamente, la media de los rangos obtenidos por los elementos de la muestra jésima y la media de los rangos del conjunto del experimento o muestra combinada. Si
H0 es cierta, estas diferencias cuadráticas tenderán a ser nulas y V estaría próximo a
cero. Por el contrario, si no fuese cierta, serían grandes y V tomaría un valor tanto más
alto cuanto mayores fuesen las diferencias entre las medias muestrales y la global de la
muestra conjunta (media del experimento en ANOVA). Tomaríamos, por tanto, la cola
derecha de la distribución
χ
2
k −1
.
No es demasiado complicado demostrar que multiplicando V por
12
, se
n(n + 1)
obtiene la expresión del estadístico H definido anteriormente. Recuérdese, para ello, que
la suma total de rangos en la muestra combinada será
global sería
n(n + 1)
y, por tanto, la media
2
(n + 1)
. Valores altos de H, por encima del punto crítico dado en las tablas,
2
serán indicadores de que existe, al menos, una mediana que es significativamente
diferente a las demás.
8
En este caso,
∑∑ r
2
ij
se puede calcular mediante [n(n+1)(2n+1)]/6 . Si hay pocas repeticiones, la
28
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 29
La existencia de una diferencia en la localización de alguna de las poblaciones,
para un nivel α de significación, se pondrá en evidencia siempre que:
R. j
−
nj
R.l
 n − 1 − H obs
> tα / 2; n − k s 2 
nl
n −1

1
 1
 + 
 n j nl 
donde Hobs representa el valor muestral del estadístico H .
Test de Friedman
Para el caso de un diseño en bloques, se puede utilizar un test no paramétrico,
llamado test de Friedman, que es una adaptación del caso anterior a las peculiaridades
de este diseño de análisis de la varianza. Los pasos a dar son los siguientes:
1. Se ordenan las respuestas observadas para las distintas muestras o
tratamientos dentro de cada uno de los bloques y se les asigna un rango que,
lógicamente, irá de 1 a k (número de tratamientos, igual al número de
observaciones por bloque). Como en el caso anterior, le llamaremos rij a
estos rangos.
2. Se obtiene la suma de rangos para cada muestra o tratamiento. Como cada
tratamiento es asignado sólo a una unidad experimental de cada bloque, esta
suma constará de a sumandos (a=número de bloques). Llamaremos R.j a esta
suma.
3. En estas circunstancias, el test queda definido como sigue:
HF =
.
k
12
R.2j − 3a (k + 1) → χ k2−1
∑
ak (k + 1) j =1
Valores altos del estadístico conducirán a rechazar la hipótesis de que las
distribuciones de los tratamientos tienen igual localización (mediana).
Hay que decir, que existe una alternativa más reciente, propuesta por Iman y
Davenport, que está basada en un test F en vez de la aproximación con la χ2, cuya
expresión es la siguiente:
aproximación sigue siendo buena.
29
A. Morillas: Análisis de la varianza (un factor). Notas de clase .
p. 30
 1 k 2 ak (k + 1) 2 
 ∑ R. j −

4
a j =1

→F
T = (a − 1) a k
( k −1),( a −1)( k −1)
k
1
2
2
rij − ∑ R. j
∑∑
a j =1
i =1 j =1
siempre que la hipótesis nula, de igualdad de localización de las poblaciones sea cierta
y se trabaje con muestras grandes. Si no hay observaciones repetidas,
∑∑ r
2
ij
= ak (k + 1)(2k + 1) / 6 , por similitud con lo dicho en la nota a pié de página
del test anterior. Este test es superior al realizado mediante HF .
Es posible realizar comparaciones múltiples, basadas en las sumas de rangos de
los tratamientos. Para un nivel α de significación, se puede afirmar que las
distribuciones de dos tratamientos difieren en localización siempre que:
R.i − R.l > tα / 2;( a −1)( k −1)
2aDobs
(a − 1)(k − 1)
donde Dobs es el valor observado para el denominador del estadístico T .
30