Ejercicios de Variables Aleatorias

Ejercicios de Variables Aleatorias
Elisa M. Molanes-López, Depto. Estadı́stica, UC3M
Función de distribución y función de densidad
Ejercicio 1. Sea X una variable aleatoria con función de distribución dada por


si x < 0
 0,
F (x) =
1 − k(1 − x),
si 0 ≤ x < k


1,
si x ≥ k.
a) Determine el valor de k para que F (x) sea, en efecto, función de distribución ¿Es X una v.a.
continua o discreta?
b) Si k = 3/4, ¿cuál es la probabilidad del suceso {1/2 < X ≤ k}?
c) Si k = 1, ¿cuál es la probabilidad del suceso {1/2 < X ≤ k}?
Solución:
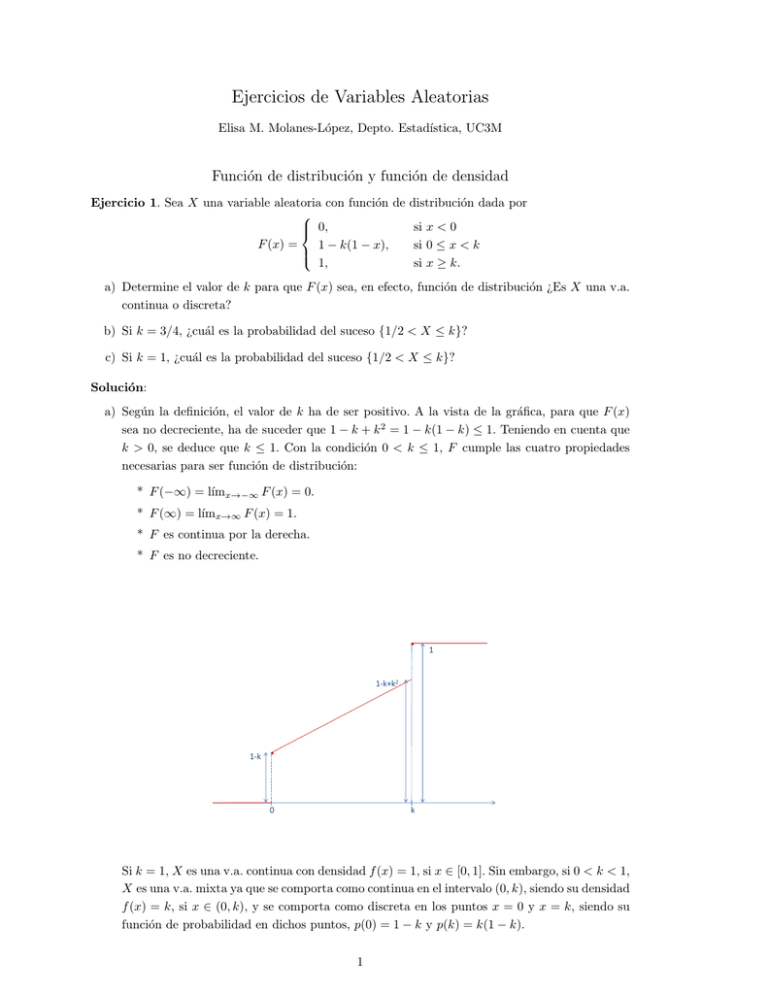
a) Según la definición, el valor de k ha de ser positivo. A la vista de la gráfica, para que F (x)
sea no decreciente, ha de suceder que 1 − k + k 2 = 1 − k(1 − k) ≤ 1. Teniendo en cuenta que
k > 0, se deduce que k ≤ 1. Con la condición 0 < k ≤ 1, F cumple las cuatro propiedades
necesarias para ser función de distribución:
* F (−∞) = lı́mx→−∞ F (x) = 0.
* F (∞) = lı́mx→∞ F (x) = 1.
* F es continua por la derecha.
* F es no decreciente.
1
1-k+k2
1-k
0
k
Si k = 1, X es una v.a. continua con densidad f (x) = 1, si x ∈ [0, 1]. Sin embargo, si 0 < k < 1,
X es una v.a. mixta ya que se comporta como continua en el intervalo (0, k), siendo su densidad
f (x) = k, si x ∈ (0, k), y se comporta como discreta en los puntos x = 0 y x = k, siendo su
función de probabilidad en dichos puntos, p(0) = 1 − k y p(k) = k(1 − k).
1
b) Si k = 3/4, resulta que:
Pr({1/2 < X ≤ k})
=
3 1
F (3/4) − F (1/2) = 1 − 1 − ×
4 2
=
3
.
8
En este caso X es una v.a. mixta. Si hubiésemos utilizado su función de densidad y su función
de probabilidad, tendrı́amos que:
Pr({1/2 < X ≤ k})
=
Pr(1/2 < X < 3/4) + Pr(X = 3/4)
Z 3/4
3
3
3
3
dx +
1−
= .
=
4
4
4
8
1/2
c) Si k = 1, resulta que:
Pr({1/2 < X ≤ k})
1
= F (1) − F (1/2) = 1 − 1 −
2
=
1
.
2
En este caso X es una v.a. continua. Si hubiésemos utilizado su función de densidad, tendrı́amos que:
Z 1
1
Pr({1/2 < X ≤ k}) =
1dx = .
2
1/2
Ejercicio 2. Sea X una v.a. con la siguiente función de distribución:
( x
e
si x ≤ 0
2 ,
F (x) =
−x
1 − e2 ,
si x > 0.
a) Indique si X es continua o discreta.
b) Determine la función de densidad de X.
c) ¿Cuál es la probabilidad del suceso {−2 ≤ X ≤ 1}?
d) ¿Cuál es la probabilidad del suceso {X = 1}?
Solución:
a) X es una v.a. continua dado que su función de distribución es continua por la derecha y por
la izquierda.
b) La función de densidad de X es
(
f (x) =
ex
2 ,
e−x
2 ,
si x ≤ 0
si x > 0.
c) Utilizando la función de distribución:
e−1
e−2
1
Pr({−2 ≤ X ≤ 1}) = F (1) − F (−2) = 1 −
−
=1−
2
2
2
1
1
+ 2
e e
= 0,7484.
Utilizando la función de densidad:
Z 0 x
Z 1 −x
e
e
1 1
1
Pr({−2 ≤ X ≤ 1}) =
dx +
dx = 1 −
+ 2 = 0,7484.
2
2 e e
−2 2
0
2
d) Para toda v.a. continua sucede que Pr(X = x) = 0, para todo x número real, de modo que
Pr({X = 1}) = 0.
Ejercicio 3. Determine el valor de k para que cada una de las siguientes funciones sea función de
densidad:
a) f (x) = kxe−kx , si x > 0.
√
√
b) f (x) = k/ 1 − x, si 0 < x < 2/2.
c) f (x) = k/(1 + x2 ), para todo x número real.
Solución: Las dos condiciones para que una función sea de densidad son las siguientes:
* f (x) ≥ 0.
R∞
* −∞ f (x)dx = 1.
a) Por la primera condición se deduce que k ≥ 0. De la segunda condición se deduce que:
Z ∞
kxe−kx dx = 1.
0
Resolviendo esta integral por partes (u = x y dv = e−kx ) y usando la regla de L’Hôpital, se
verifica que:
Z ∞ −kx
x=∞
1
x
e−kx
e
x
= .
− lı́m
+
dx = −
1 = k lı́m
x→∞ −kekx
x→0 −kekx
k
k
k
0
x=0
De donde se concluye que k = 1.
b) Por la primera condición se deduce que k ≥ 0. De la segunda condición se deduce que:
√
Z
2/2
0
k
dx = 1.
(1 − x)1/2
Resolviendo esta integral, se verifica que:
 s

s
√
√
√2/2
(1 − x)1/2
2
2
1 = −k
= −2k 1 −
+ 2k = k −2 1 −
+ 2 = 0,9176k.
1/2
2
2
0
De donde se concluye que k = 1,0898.
c) Por la primera condición se deduce que k ≥ 0. De la segunda condición se deduce que:
Z ∞
k
dx = 1.
2
−∞ 1 + x
Resolviendo esta integral, se verifica que:
1
∞
= k arctan(x)]−∞ = k
De donde se concluye que k = 1/π.
3
π
π − −
= πk.
2
2
Ejercicio 4. El tiempo de retraso, medido en minutos, del AVE Sevilla - Madrid sigue una variable
aleatoria continua con función de distribución

0,
si x ≤ −1



 k(x + 1) + x2 −1 ,
si
−1<x≤0
2
F (x) =
x2 +1

k(x + 1) − 2 ,
si 0 < x ≤ 1



1,
si x > 1.
a) Calcule el valor de k.
b) Calcule la probabilidad de que el tren llegue con menos de medio minuto de retraso.
c) Calcule la probabilidad de que el tren llegue antes de la hora prevista.
d) Calcule el tiempo esperado de retraso.
e) Calcule la probabilidad de que el tren llegue entre medio minuto de adelanto y un minuto de
retraso.
f) Sabiendo que el tren ha llegado con retraso, calcule la probabilidad de que lo haya hecho
menos de 15 segundos después de lo previsto.
Solución: Sea X la v.a. que mide el tiempo de retraso en minutos del AVE Sevilla - Madrid. Notése
que cuando X < 0 significa que la llegada del tren se ha producido con antelación a su tiempo de
llegada previsto. En cambio, si X > 0, entonces el tren habrá llegado con retraso.
a) Al ser X una v.a. continua, sabemos que su función de distribución, F , ha de ser continua en
todo punto. De modo que, lı́mx→1+ F (x) = F (1) ⇒ 1 = 2k − 1 ⇒ k = 1.
b) Pr(X < 0,5 min) = F (0,5) = (0,5 + 1) −
c) Pr(X < 0) = F (0) = 1 −
1
2
(0,5)2 +1
2
=
7
8
= 0,875 = 87,5 %.
= 0,5 = 50 %.
d) En el caso de una v.a. continua su media o esperanza se calcula integrando en todo < su
función de densidad, f (x), multiplicada por x, es decir,
Z ∞
E[X] =
xf (x)dx.
−∞
Calculemos en primer lugar, f (x) =
dF
dx (x).
Se tiene que:


 1 + x,
f (x) =
1 − x,


0,
si − 1 < x ≤ 0
si 0 < x ≤ 1
en caso contrario.
Entonces,
Z
E[X]
0
=
Z
−1
1
x(1 − x)dx = 0.
x(1 + x)dx +
0
e) Pr(−0,5 min < X < 1 min) = F (1) − F (−0,5) =
7
8
= 0,875 = 87,5 %.
f) Para calcular Pr(X < 41 |X > 0) hacemos uso de la definición de probabilidad condicionada:
1
Pr X < |X > 0
4
=
Pr(0 < X < 14 )
F (1/4) − F (0)
7
=
=
= 0,4375 = 43,75 %.
Pr(X > 0)
1 − F (0)
16
4
Ejercicio 5. Un autobús pasa por una cierta parada cada 8 minutos. Si un usuario llega a la
parada, el tiempo que debe esperar es una variable aleatoria con función de densidad f1 (t) (t en
minutos). Sin embargo, si el autobús lleva retraso, el tiempo de espera se distribuye según la función
de densidad f2 (t).
(
1/8,
si 0 < t < 8
f1 (t) =
0,
en caso contrario.
(
f2 (t) =
1 −t/10
,
10 e
0,
si t > 0
en caso contrario.
Sabiendo que un dı́a de cada tres, el autobús llega con retraso, calcule la probabilidad de que el
usuario tenga que esperar más de 5 minutos.
Solución: En este ejercicio aplicaremos el Teorema de la Probabilidad Total.
Sea R el suceso ((el autobús lleva retraso un dı́a concreto)). Sabemos que Pr(R) = 1/3, de modo que
Pr(R) = 2/3.
Nos piden Pr(T > 5 min), siendo T la v.a. que mide el tiempo que un usuario de dicho autobús
espera en la parada hasta que éste llega.
Usando como partición del espacio muestral los sucesos R y R, el Teorema de la Probabilidad Total
nos permite escribir Pr(T > 5 min) como sigue:
Pr(T > 5 min)
=
Pr(T > 5 min|R) Pr(R) + Pr(T > 5 min|R) Pr(R).
Calculemos Pr(T > 5 min|R) y Pr(T > 5 min|R):
Z ∞
it=∞
Pr(T > 5 min|R) =
f2 (t)dt = e−t/10
= e−0,5 ,
t=5
5
Z
Pr(T > 5 min|R)
=
5
8
t
1
dt =
8
8
t=8
=
t=5
3
.
8
Se concluye que:
Pr(T > 5 min)
=
e−0,5 ×
1 3 2
+ × = 0,4522 = 45,22 %.
3 8 3
5