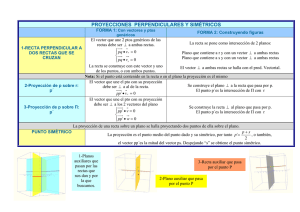
Geometr´ıa Anal´ıtica II 1 Distancia entre dos rectas
Anuncio
Anuncio