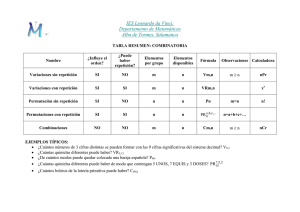
RESUMEN DE COMBINATORIA

Departamento de Matemáticas
RESUMEN DE COMBINATORIA.
Según la definición de la Real Academia de la Lengua la combinatoria es “La parte de las
matemáticas que estudia el número de posibilidades de ordenación, selección e intercambio
de los elementos de un conjunto, es decir, las combinaciones, variaciones y permutaciones.”
La pregunta que nos haremos en cada caso es de cuántas formas se puede hacer.
¿Cuántas agrupaciones se pueden formar con los elementos de un conjunto?
REGLA DEL PRODUCTO
Si una elección tiene N alternativas posibles y otra elección distinta tiene M alternativas
posibles, entonces la realización de ambas elecciones, una tras otra, tiene NxM alternativas
distintas.
• Ejemplo 1:
Tenemos 3 camisas y 2 pantalones, ¿de cuántas formas diferentes podremos vestirnos?
3 alternativas posibles
Camisas {C1, C2, C3}
Pantalones {P1, P2}
2 alternativas posibles
Una elección 1 es una pareja {C, P}. Puede haber 6 maneras (3x2), pues para cada una de las 3
camisas puede elegir 2 pantalones:
{C1, P1}
{C1, P2}
{C2, P1}
{C2, P2}
{C3, P1}
{C3, P2}
• Ejemplo 2:
“Si en un restaurante en la carta contiene 6 primeros platos, 5 segundos platos y 8 postres.
¿Cuántos menús diferentes podrá servir el restaurante? 2
Primeros {P1, P2, P3, P4, P5, P6}
6 alternativas posibles
Segundo: {S1, S2, S3, S4, S5}
5 alternativas posibles
8 alternativas posibles
Postre: {T1, T2, T3, T4, T5, T6, T7, T8}
Un elección (un menú) consiste en una terna {P, S, T}. El primero se puede seleccionar de 6
formas, el segundo de 5 formas y el postre de 8 formas; por lo tanto habrá 240 menús
(6x5x8).
{P1, S1, T1} {P1, S1, T2} {P1, S1, T3} {P1, S1, T4} {P1, S1, T5} {P1, S1, T6}
{P1, S1, T7} {P1, S1, T8}
{P1, S2, T1} {P1, S2, T2} {P1, S2, T3} {P1, S2, T4} {P1, S2, T5} {P1, S2, T6}
{P1, S2, T7} {P1, S2, T8}
{P1, S3, T1} {P1, S3, T2} {P1, S3, T3} {P1, S3, T4} {P1, S3, T5} {P1, S3, T6}
{P1, S3, T7} {P1, S3, T8}
…
{P6, S5, T1} {P6, S5, T2} {P6, S5, T3} {P6, S5, T4} {P6, S5, T5} {P6, S5, T6}
{P6, S5, T7} {P6, S5, T8}
• Caso general:
Si un objeto A1 se puede seleccionar de p1 maneras, un objeto A2 se puede seleccionar de p2
maneras, un objeto A3 se puede seleccionar de p3 maneras, y así sucesivamente hasta
seleccionar el objeto An, que se pueda seleccionar de pn maneras,
Entonces los modos de seleccionar los n-objetos juntos {A1, A2, …, An} son p1xp2x…xpn .
Debes tener muy claro qué es n y qué es m en cada tipo de problema:
1
2
Una agrupación, una alternativa, una manera, una forma, un modo, una selección …
¿De cuántas formas se puede hacer: elegir un menú?
1
Departamento de Matemáticas
n es el número de objetos que hay en cada selección
m es el número de objetos que hay para seleccionar
VARIACIONES SIN REPETICIÓN O VARIACIONES ORDINARIAS
• ¿De cuántos modos diferentes se pueden repartir las medallas de oro, plata y bronce
los 8 atletas de una carrera?
Sean {A, B, C, D, E, F, G, H} los atletas (los objetos): m=8
Cada agrupación (podium) tiene 3 objetos: n=3.
Una podría ser {A, D,G}, A oro, D plata y G bronce.
¿Pueden repetirse? No,
{A, A, G}, un atleta no puede recibir 2 medallas
¿Influye el orden? Si
{A, D, G} ≠ {D, A, G}, en el primer podium el oro es para A y en el segundo para D, se han
tomado los mismos objetos, atletas, pero son diferentes selecciones.
8!
8!
V8,3 =
= = 8 ⋅ 7 ⋅ 6 = 336
(8 − 3)! 5!
Con la calculadora 8 n Pr 3 = 336
Enlace a la calculadora WIRIS: http://www.educa.jcyl.es/wiris/es/index.html
El comando V8,3 produce 336
El comando V{A,B,C,D,E,D,G,H},3 produce todos los podiums posibles.
VARIACIONES CON REPETICIÓN
• ¿Cuántas palabras de 3 letras, con o sin sentido, pueden hacerse con las letras A, B, C,
D, E, F?
Las letras son {A, B, C, D, E, F}: m=6.
Cada palabra tiene 3 letras: n=3
Una palabra podrías ser ADD
¿Pueden repetirse? Si.
La palabra ADD tiene 2 letras iguales
¿Influye el orden? Si
La palabra ADD es diferente de DAD
VR 6,3 = 63 = 216
Con la calculadora: 6 x y 3 = 216
Enlace a la calculadora WIRIS: http://www.educa.jcyl.es/wiris/es/index.html
El comando VR6,3 produce 216
El comando VR{A,B,C,D,E,F},3 produce todas las palabras distintas de 3 letras que pueden
hacerse con las letras A, B, C, D, E, F.
PERMUTACIONES SIN REPETICIÓN
2
Departamento de Matemáticas
• ¿De cuántas formas pueden quedar clasificados 5 atletas en una
carrera?
Sean {A, B, C, D, E } los atletas (los objetos): m=5
Cada agrupación (clasificación) tiene 5 objetos: n=5.
Una posible clasificación es {A,C,D,E,B}, siendo A el 1º, C el 2º,… y B el 5º.
¿Pueden repetirse? No.
Un mismo atleta no puede quedar 1º y 2º, la agrupación {A,A,B,C,D} no es posible.
¿Influye el orden? Si
{A,B,C,D,E}≠{B,A,C,D,E}
Son variaciones ordinarias de 5 elementos tomados de 5 en 5.
V5,5 = P5 = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅1 = 120
Con la calculadora: 5 n! = 120
Enlace a la calculadora WIRIS: http://www.educa.jcyl.es/wiris/es/index.html
El comando P5 produce 120
El comando P{A,B,C,D,E} produce las 120 permutaciones de 5 elementos.
PERMUTACIONES CON REPETICIÓN
• ¿Cuántas quinielas hay que tengan 7 UNOS, 5 EQUIS y 3 DOSES.
Cada una de las agrupaciones tiene 15 elementos, n=15.
Disponemos de 15 elementos: 7(unos)+5(equis)+3(doses)=15
Una agrupación será una quiniela, por ejemplo {111X22XX12111XX}
¿Influye el orden? Si.
¿Puede haber repetición? Si.
Son permutaciones con repetición de 15 elementos en las que hay 7 repetidas, 5 repetidas y 3
repetidas.
15!
PR15
= 360360
7,5,3 =
7!⋅ 5!⋅ 3!
Con la calculadora: habría que hacer la operación 15!:(7!x5!x3!)
Enlace a la calculadora WIRIS: http://www.educa.jcyl.es/wiris/es/index.html
7,5,3
El comando P15
produce 360360.
{1,1,1,1,1,1,1,X,X,X,X,X,2,2,2} produciría las 360360 quinielas solicitadas, pero la
El comando P14
capacidad técnica de la misma agota su memoria.
{1,1,1,X,X,2,2}
Puedes probar con P7
3
Departamento de Matemáticas
COMBINACIONES SIN REPETICIÓN.
Dados los 7 colores del arco iris, ¿cuántas mezclas de 3 colores distintos podremos
formar?
Disponemos de 7 elementos, los 7 colores del arco iris: m=7.
Cada una de las agrupaciones tiene 3 colores: n=3.
Sean los colores {A, B, C, D, E, F, G}.
Una agrupación es una mezcla de 3 colores, por ejemplo {A, B, G}
¿Influye el orden? No.
El color resultante de tomar {A, B, G} es el mismo que el de tomar {B, A, G}
¿Puede haber repetición? No.
La mezcla {A, A, B} sólo contiene 2 colores del arco iris.
Son combinaciones sin repetición de 7 elementos tomados en grupos de 3 elementos.
7!
C7,3 =
= 35
3!⋅ (7 − 3)!
•
Con la calculadora 7 nCr 3 = 35
Enlace a la calculadora WIRIS: http://www.educa.jcyl.es/wiris/es/index.html
El comando C7,3 produce 35.
El comando C{A,B,C,D,E,F,G},3 produce los 35 colores-mezcla diferentes.
4