Ejercicio nº 1.- a) Indica cuáles de los siguientes números son

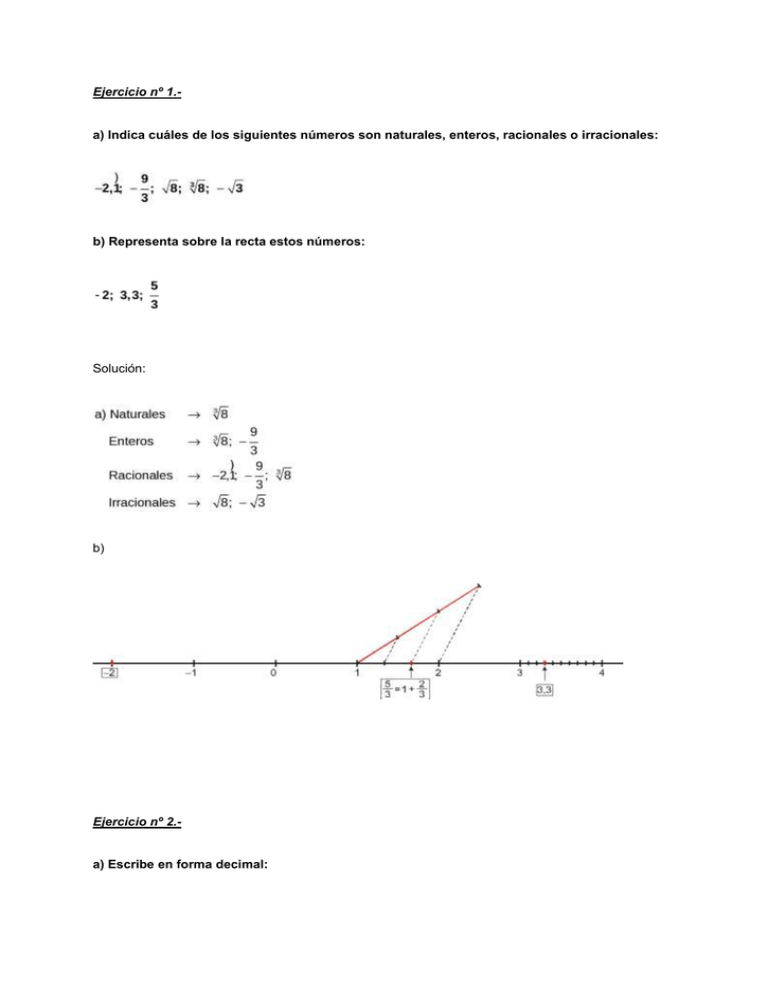
Ejercicio nº 1.-
a) Indica cuáles de los siguientes números son naturales, enteros, racionales o irracionales:
b) Representa sobre la recta estos números:
Solución:
b)
Ejercicio nº 2.-
a) Escribe en forma decimal:
b) Escribe en forma de fracción irreducible:
Solución:
a) Efectuamos la división en cada caso:
b)
Ejercicio nº 3.-
a) Calcula:
b) Reduce a una sola potencia:
Solución:
Ejercicio nº 4.-
a) Opera y simplifica el resultado:
b) Calcula y simplifica:
Solución:
Ejercicio nº 5.-
a) Calcula:
-6
-5
-7
7,08 × 10 - 1,01 × 10 - 2,01 × 10
b) Calcula:
Solución:
-6
-5
-7
-6
-6
-6
a) 7,08 × 10 - 1,01 × 10 - 2,01 × 10 = 7,08 × 10 - 10,1 × 10 - 0,201 × 10 =
-6
= (7,08 - 10,1 - 0,201) × 10 = -3,221 × 10
b)
-6
Ejercicio nº 6.-
Simplifica las expresiones que puedas y en las restantes indica por qué no se puede
simplificar:
Solución:
Ejercicio nº 7.-
Un trabajador ha realizado las 2/7 partes de un encargo; otro realizó 2/5 partes, y un tercero lo
terminó. Si les pagan en total 1 008 €, ¿cuánto le corresponderá a cada uno?
Solución:
Ejercicio nº 8.-
Mezclamos mediante fundición 4,5 kg de oro con una pureza del 85% con 2,5 kg de oro de
pureza 74%. ¿Cuál será la pureza de la mezcla? ¿Qué ley tendrá el oro obtenido?
Nota: El oro puro tiene una ley de 24 quilates.
Solución:
Componentes
Cantidad (kg)
Riqueza
Cantidad de oro puro
(kg)
1.º
4,5
85%
3,825
2.º
2,5
74%
1,85
Mezcla
7
3,825 + 1,85 = 5,675
La proporción de oro en la mezcla será: 5 675 : 7 = 0,810 = 81%.
La ley del oro obtenido será: 24 · 0,810 = 19,44 quilates.
Ejercicio nº 9.-
Se han pagado 1 202 € por un ordenador. Si el IVA aplicado ha sido del 16%. ¿Cuál era el
precio inicial del ordenador?
Solución:
Precio final = 1 202 €
Subida de un 16% → Índice de variación = 1,16
1 036,21 €
El precio inicial del ordenador era de 1 036,21 €.
Ejercicio nº 10.-
En una progresión geométrica de razón positiva, sabemos que a2 = 10 y a4 = 40. Calcula la
razón y la suma de los 9 primeros términos.
Solución:
8
8
a9 = a1 · r = 5 · 2 = 5 · 256 = 1 280 → a9 = 1 280
Ejercicio nº 11.-
En un cine, la segunda fila de butacas está a 10 metros de la pantalla, y la séptima fila está a
16 metros. ¿En qué fila debe sentarse una persona a la que le guste ver la pantalla a una
distancia de 28 metros?
Solución:
La distancia de cada fila de butacas a la pantalla son los términos de una progresión aritmética.
Sabemos que a2= 10 m y a7= 16 m.
Buscamos n tal que an= 28 m.
a7= a2 d 16 = 10 + 5d → 6 = 5d d 1,2 m
a1= a2 d 10 - 1,2 = 8,8 m → a1= 8,8 m
an= a1+ (n - 1) · d → 28 = 8,8 + (n - 1) · 1,2
28 = 8,8 + 1,2n - 1,2 → 20,4 = 1,2n → n = 17
Deberá sentarse en la fila 17.
Ejercicio nº 12.-
La suma de los infinitos términos de una progresión geométrica es -60 y el primer término es 36. Halla la razón.
Solución: