E24 Vaciado De Estanque

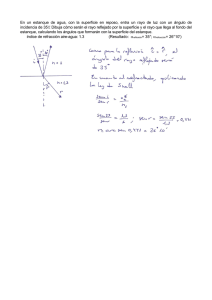
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
INGENIERIA DE EJECUCIÓN EN MECANICA
PROGRAMA PROSECUCION DE ESTUDIOS
VESPERTINO
GUIA DE LABORATORIO
ASIGNATURA
9555 M85 MECÁNICA DE FLUIDOS
NIVEL 03
EXPERIENCIA E-24
“VACIADO DE ESTANQUE”
HORARIO: SÁBADO 3-4-5-6
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
EXPERIENCIA E-24 VACIADO DE ESTANQUE
1.
OBJETIVO GENERAL
Como una aplicación de la Ecuación de Bernoulli para flujos incompresibles, se estudian todos
los parámetros que permiten evaluar el vaciado de un estanque. De esta forma encontrar el
error en los modelos matemáticos pertinentes.
2.
OBJETIVOS ESPECÍFICOS
2.1.
Determinar experimentalmente el coeficiente de descarga o de caudal por un orificio de pared
delgada.
2.2.
Determinar experimentalmente el coeficiente de velocidad.
2.3.
Determinar experimentalmente el coeficiente de contracción.
2.4.
Determinar la Pérdida de Energía.
2.5.
Influencia de la altura de carga en el alcance de un chorro horizontal.
2.6.
Determinar el error porcentual del modelo matemático para el tiempo de vaciado de
estanques.
2.7.
Influencia de “Hc” en el error del modelo matemático.
2.8.
Generar gráficos experimentales que permitan determinar la influencia de la altura de
descarga en los coeficientes de contracción, descarga y velocidad.
3.
CONSIDERACIONES TEÓRICAS
Cuando se estudia el problema del vaciado de un estanque se observa que se está frente a un
problema de régimen variable en el tiempo. El tiempo de vaciado resulta un problema práctico
interesante. El orificio de descarga puede estar ubicado en alguna pared lateral o en el fondo,
y terminar en un tubo o tobera.
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
Figura 1
La figura 1 muestra tres casos típicos de vaciado de un estanque por un orificio de pared
delgada.
a)
Se observa que existe chorro libre y superficie del estanque en contacto con la atmósfera.
b)
Chorro de líquido sumergido y superficie del estanque en contacto con la atmósfera.
c)
Depósito no abierto a la atmósfera. En este caso particular las presiones en 1) pueden ser
mayores o menores que la atmosférica.
Consideremos para el caso a) un balance de energía entre la superficie libre (1) y la salida por
el orificio (2). Si en primera instancia se considera que no existen pérdidas de energía se
tendrá:
P1
V2
P
V2
 1  h  2  2  0
 o g 2g
 o g 2g
Considerando que P1 = 0 (manométrico) que se estima V1 = 0 en la superficie de los
estanques y P2 = 0 (manométrico) resulta:
V2  2 g h
(1)
La solución (1) es teórica, sin embargo es posible encontrar la velocidad REAL si se considera
la existencia de un coeficiente de velocidad “CV”
V  CV
2 g h
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
Es posible determinar experimentalmente dicho coeficiente mediante:
Figura 2
Según fig. (2) la trayectoria de la vena fluida es parabólica con ángulo de salida cero. Al no
considerar la resistencia con el aire se cumple

X a  t Cv
Ya 
2 g h

1
2
g t 
2
(2)
(3)
Técnicamente a “Xa” se le denomina “Alcance del Chorro”. En el mismo instante “t” se logran
“Xa” e “Ya”. Usando ecuaciones (2) y (3) se obtiene:
Cv 
Xa
2
1
h Ya
(4)
donde los valores de Xa e Ya son obtenidos en el Laboratorio.
Cuando el chorro sale del orificio sufre una contracción, como se indica en la figura (1) (a), es
decir si el orificio posee un área física real “Ao” el chorro genera un área “Ac”.
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
De esta forma se define un coeficiente de contracción “”:

luego
Ac
Ao
(5)
Ac =  · Ao
(6)
Es posible entonces determinar el caudal que sale por el orificio, considerando velocidades
reales y área real.
Dicho caudal estará dado por:
Q   · Cv A 2 g h
se acostumbra a nominar  · Cv = m, llamado coeficiente de descarga. Luego el caudal
queda:
Q  m· A 2 g h
(7)
El modelo (7) se cumple siempre que la altura de carga h sea constante, lo cual se consigue
si el caudal que ingresa al estanque es el mismo al que sale por el orificio del estanque.
Figura 3
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
La figura (3) muestra un estanque de área variable.
El problema consiste en determinar cual es el tiempo de vaciado entre las alturas de carga “h1”
y “h2”, cuando se suspende el suministro al estanque. Se observa que se está frente a un
problema de flujo impermanente.
Q
d
dt
(8)
En un instante dt de tiempo el diferencial de volumen que desciende en la misma magnitud
que lo hace salir del orificio.
d = dh A
(9)
donde A = área variable del estanque (fig. 3)
Se cumple que:
d
 m Ao
dt
dh A
 m Ao
dt
dt 
t

2g h
2g h
A
m Ao
2g
h1
A
h2
m Ao
h 1 / 2 dh
2g
h 1 / 2dh
(10)
Durante el desarrollo del experimento se observaran la influencia de “A” y “m” en los valores
del tiempo de vaciado del estanque. Por ejemplo si el estanque es de sección regular “A”
queda fuera de la integral.
4.
PROCEDIMIENTO
4.1.
Reconocer el equipo experimental.
4.2.
Desarrollar los objetivos planteados.
4.3.
Determinar las variables a medir.
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE INGENIERÍA
Departamento de Ingeniería Mecánica
Programa Vespertino de Prosecución de Estudios
Ingeniería de Ejecución en Mecánica
4.4.
Seleccionar instrumentos y aparatos.
4.5.
Planificar adecuadamente (cuadro).
4.6.
Efectuar mediciones.
4.7.
Tabular
4.8.
Efectuar un análisis de consistencia de los valores experimentales.
4.9.
Construir un esquema del equipo usado.
5.
BIBLIOGRAFIA

Claudio Mataix, “Mecánica de Fluidos y Máquinas Hidráulicas”, HARLA.

Irving Shames, “Mecánica de Fluidos”, Mc Graw Hill.