ϕ φ φ φ φ

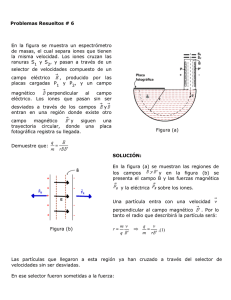
27.6 Un electrón se traslada a 2.5 106 m/s a través de una región en la que
hay un campo magnético de dirección no especificada y cuya magnitud es de
7.4 10-2 T.
a)¿Cuáles son las magnitudes máxima y mínima posibles de la aceleración del
electrón debida al campo magnético?
b) Si la aceleración real del electrón es de ¼ de la magnitud máxima del inciso
(a), ¿cuál es el ángulo entre la velocidad del electrón y el campo magnético?
r
r
a) F = ma = qvB sin(ϕ )
amax
qvB (1.6 10 −19 C )(2.5 10 6 m / s )(0.074T )
16
2
=
=
=
3
.
25
10
m
/
s
m
9.11 10 −31 kg
amin = 0
b) a = 0.812 1016 m / s 2
a=
qvB sin(φ )
ma
⇒ sin(φ ) =
m
qvB
(9.11 10 −31 kg )(0.812 1016 m / s 2 )
o
sin(φ ) =
0
.
25
14
.
4
=
φ
=
(1.6 10 −19 C )(2.5 10 6 m / s )(0.074T )
27.14 Una partícula con una carga de 6.4 10-19 C recorre una órbita circular de
4.68 mm de radio debido a la fuerza que sobre ella ejerce un campo magnético
uniforme B=1.65 T y perpendicular a la órbita.
a)¿Cuál es la magnitud de la cantidad de movimiento lineal p=mv de la partícula?
b)¿Cuál es la magnitud de la cantidad de movimiento angular L de la partícula?
a) R =
mv
qB
⇒ mv = RqB = (0.00468m)(6.4 10 −19 C )(1.65T ) = 0.0494 10 −19 kg (m / s )
b) L = R(mv) = 2.3110 −23 kg (m 2 / s )
27.21 El deuterón (el núcleo de un isótopo de hidrógeno) tiene una masa de 3.34
10-27 kg y una carga de +1.6 10-19 C. Un deuterón recorre una trayectoria
circular de 6.96 mm de radio en un campo magnético cuya magnitud es de
2.5 T.
a) Halle la rapidez del deuterón;
b) Halle el tiempo que requiere para completar media revolución;
c) ¿A través de qué diferencia de potencial habría que acelerar el deuterón
para que adquiriese esta rapidez?
v2
qBR (1.6 10 −19 C )(2.5T )(0.0069m)
5
a ) qvB = m ⇒ v =
=
=
8
.
33
10
m/s
− 27
R
m
3.34 10 kg
2πm 2π (3.34 10 −27 kg )
−8
b) T =
=
=
=
5
.
24
10
s
−19
qB (1.6 10 C )(2.5T )
ω
2π
T
t = = 2.62 10 −8 s
2
c)
1 2
K = mv = q∆V
2
1 mv 2 1 (3.34 10 − 27 kg )(8.33 105 m / s ) 2
∆V =
=
= 7242V
−19
2 q
2
1.6 10 C
APLICACIONES DEL MOVIMIENTO DE PARTÍCULAS CON CARGA
SELECTOR DE VELOCIDAD
Fuente
+q
X- X
X X
-
v
X- X
X
-
+X
+
+
X
B
+X
+
X
+
X
E
Fe=qE
Fm=qvB
v
En un haz de partículas con carga producido por un cátodo
caliente o un material radioactivo no todas las partículas se
trasladan con la misma rapidez. En muchas aplicaciones se
requiere un haz en que la rapidez de todas las partículas sea la
misma. Se pueden seleccionar partículas del haz con una rapidez
específica mediante una configuración de campos eléctricos y
magnéticos llamada selector de velocidad.
Para magnitudes de campo dadas E y B, con respecto a
un valor particular de v las fuerzas eléctrica y
magnética serán de igual magnitud:
qE = qvB
E
v=
B
EXPERIMENTO DE THOMSON
J.J. Thomson logró medir la relación e/m de carga a masa del electrón en
1897. En un recipiente de vidrio al alto vacío, se aceleran electrones
provenientes del cátodo C y se reúnen en un haz mediante una diferencia de
potencial V entre los ánodos A y A’. La rapidez v de los electrones está
determinada por el potencial V:
1 2
mv = qV
2
v=
2qV
m
Los electrones pasan entre las placas P y P’ en inciden en la pantalla del
extremo del tubo, la cual está recubierta de un material fluorescente que
emite luz en el punto de impacto.
Los electrones pasan en línea recta entre las placas cuando:
E
2qV
v= =
B
m
q
E2
=
m 2VB 2
Thomson encontró un solo valor de esta magnitud, no dependía ni del
material del cátodo, ni del gas residual presente en el tubo, ni de ningún
otro aspecto del experimento. Esta independencia demostró que las
partículas del haz (electrones) son un componente de toda la materia.
q
= 1.758820174 1011 C / kg
m
ESPECTRÓMETROS DE MASAS
Se pueden emplear técnicas similares al experimento de Thomson para medir
masas de iones, y de este modo, medir masas atómicas y moleculares.
S1
S2
-
+
+
v -
+
B
+
Placa
+
fotográfica
m2
E
-
Los iones entran en una región con campo
magnético donde se trasladan en arcos
circulares de radio R:
-
m1
R2
R1
Los iones positivos provenientes de una
fuente pasa a través de las ranuras S1 y S2,
y forman un haz estrecho. Los iones
atraviesan un selector de velocidad para
bloquear todos los iones salvo aquellos con
rapidez v=E/B.
B
R=
mv
qB
Los iones con masas diferentes inciden en la placa fotográfica en puntos
diferentes y se pueden medir los valores de R.
27.28 a) ¿Cuál es la rapidez de un haz de electrones cuando la influencia
simultánea de un campo eléctrico de 1.56 104 V/m y un campo magnético de
4.62 10-3 T, con ambos campos normales al haz y entre sí, no desvían los
electrones? b) Cuando se elimina el campo eléctrico, ¿cuál es el radio de la
órbita del electrón? ¿Cuál es el periodo de la órbita?
a ) qE = qvB
E 1.56 10 4 V / m
6
=
3
.
3
10
m/s
v= =
−3
B
4.62 10 T
v2
b) qvB = m
R
mv (9.1 10 −31 kg )(3.3 106 m / s)
−3
R=
=
=
4
.
06
10
m
−19
−3
qB (1.6 10 C )(4.62 10 T )
2πm
2π (9.1 10 −31 kg )
−9
T=
=
=
=
7
.
73
10
s
−19
−3
ω
qB (1.6 10 C )(4.62 10 T )
2π
27.29 Un selector de velocidad se compone de un campo eléctrico y uno magnético. a)
¿Cuál debe ser la intensidad del campo magnético para que sólo los iones con una rapidez
de 2000 km/s emerjan sin desviación, si el campo eléctrico es 2 105 V/m? ¿Se separarán
los iones positivos de los iones negativos? b) En cierto selector de velocidad, el campo
eléctrico se produce mediante una batería de voltaje variable, conectada a dos placas
metálicas paralelas grandes separadas 3.25 cm, y el campo magnético proviene de un
electroimán de intensidad de campo variable. Si el voltaje de la batería puede fluctuar
entre 120 V y 560 V, y el campo magnético entre 0.054 T y 0.18 T, ¿cuál es el intervalo de
velocidades de iones que puede producir este selector con los ajustes correspondientes?
a)
b)
E
E 2 105V / m
=v B= =
= 0.1T
6
B
v 2 10 m / s
E=
V
d
120V
560V
= 36.9 10 2 V / m Emax =
= 172.3 10 2 V / m
0.0325m
0.0325m
= 0.054T , Bmax = 0.18T
Emin =
Bmin
No se separan
vmax
Emax 172.3 10 2 V / m
=
=
= 3190.8 10 2 m / s
Bmin
0.054T
vmin
Emin 36.9 10 2 V / m
=
=
= 2.05 10 4 m / s
Bmax
0.18T
27.32 En un espectrómetro de masas, la magnitud del campo magnético del
selector de velocidad es de 0.650 T y los iones cuya rapidez es 1.82 106
m/s lo atraviesan sin desviarse.
a) ¿Cuál es la magnitud del campo eléctrico del selector de velocidad?
b) ¿Cuál es el cociente entre la masa y la carga de los iones cuyo radio de la
trayectoria circular hacia la placa fotográfica es de 0.2 mm, si el campo
magnético es B=0.8 T?
E = Bv = (0.65T )(1.82 106 m / s ) = 1.18 106 V / m
mv
R=
qB
m RB (0.2 10 −3 m)(0.8T )
−9
0
.
29
10
=
=
=
kg / C
6
1.82 10 m / s
q
v