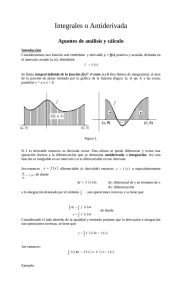
una aproximación a un problema clásico de la integral de riemann

UNA APROXIMACIÓN A UN PROBLEMA CLÁSICO
DE LA INTEGRAL DE RIEMANN
Comunicación efectuada por el Lic. Roberto Depaoli
en la Academia Nacional de Ciencias de Buenos Aires
en la sesión privada extraordinaria del 20 de diciembre de 2007
Abstract
The Riemann integral’s definition was formulated in the nineteenth
century and introduced the question about identification of integrable
functions.
Supported on the concept of oscillation of a function in a point, Du Bois
Reymond established a necessary and sufficient condition for the existence
of the Riemann integral. Vito Volterra (1881) exhibited a function defined in
a real interval, whose derivative is bounded and is not Riemann integrable.
Hence, he found a limitation in the scope of second fundamental theorem of
integral calculus. In this article, another example is constructed.
The points with positive oscillation are exactly the points of
discontinuity of a function. The aim to measure the set of these points
generated the ideas whose evolution prepared the conditions for Lebesgue’s
works on measure and integration, at the beginning of twentieth century.
Resumen
La definición de integral propuesta por Riemann en el siglo XIX, planteaba el problema de identificar a las funciones integrables. Basado en el concepto
de oscilación de una función en un punto, Du Bois Reymond estableció una
condición necesaria y suficiente para la existencia de la integral de Riemann.
Vito Volterra (1881) exhibió una función definida en un intervalo real, cuya derivada está definida en todo punto, es acotada y no es integrable Riemann,
fijando con ello una restricción al alcance del segundo teorema fundamental
del cálculo. En este artículo se construye un ejemplo alternativo.
Los puntos de oscilación positiva son exactamente las discontinuidades de
una función. El intento de medir el conjunto de ellas dio origen al concepto de
contenido, cuya evolución preparó el terreno para la formulación, por parte de
Lebesgue, de su teoría de la medida y la integración, a comienzos del siglo XX.
1. Introducción
Con la teoría de la integral de Riemann, el segundo teorema fundamental del cálculo expresa lo siguiente:
Si f:[a,b]→ R es continua en el intervalo cerrado [a,b]
, derivable en
todo punto del intervalo abierto (a,b)y, además, existe g :[a,b]→ R
integrable Riemann, tal que:
485
entonces:
x ∈ (a,b)
g(x)= f′(x)
La tesis de este teorema puede ser puesta en la forma equivalente:
x
f(x)= f(a)+ R ∫ f′(t)dt
∀x∈ [a,b]
a
El teorema garantiza la reconstrucción de la función fa partir de
su derivada, si fes derivable en todo punto de (a,b)y su derivada es
integrable Riemann.
Se puede formular una condición necesaria y suficiente para la
integrabilidad Riemann con el concepto de medida de Lebesgue, de la
siguiente manera:
Sea f:[a,b]→ R una función acotada. Entonces:
fes integrable Riemann si y sólo si el conjunto de puntos de discontinuidad de ftiene medida de Lebesgue nula.
Además, la utilización de la integral de Lebesgue amplía el alcance del teorema mencionado anteriormente:
Si f:[a,b]→ R es una función absolutamente continua, entonces
f′(x)existe para casi todo punto del intervalo (a,b), f′ es una función
medible e integrable Lebesgue y, además:
x ∈ [a,b]
En esta presentación, se muestra que la hipótesis de que la derivada de fexiste en todo punto y es una función acotada, no basta
para probar la versión de Riemann del teorema.
A tal fin, se construye una función fcon las características indicadas, para la cual existen incluso las derivadas laterales en a y b,
pero con la propiedad de que el conjunto de discontinuidades de su
derivada tiene medida de Lebesgue positiva. Resulta entonces que f
no es integrable Riemann.
Por otra parte, la función fes absolutamente continua, ya que su
derivada existe en todo punto y es acotada. Entonces es posible aplicarle el teorema en la versión de Lebesgue.
En definitiva, el segundo teorema fundamental del cálculo no
asegura la reconstrucción de una función mediante la integral de
486
Riemann, si sólo se supone que su derivada existe en todo punto y es
acotada. Sin embargo, con estas condiciones, siempre se la puede reconstruir con la integral de Lebesgue.
El problema presentado en este artículo constituyó una preocupación para los matemáticos de la segunda mitad del siglo XIX, como
consecuencia de la definición de integrabilidad propuesta por Riemann, que dejaba pendiente la caracterización de las funciones integrables. Se intuía que la integrabilidad estaba fuertemente vinculada
con las discontinuidades de la función.
Considerando que la oscilación de una función en un punto es mayor que cero si y sólo si se trata de un punto de discontinuidad, Du
Bois Reymond proporcionó una condición necesaria y suficiente de
integrabilidad Riemann. En 1881, Vito Volterra, sobre la base de esta
condición, construyó una función derivable en todo punto, cuya derivada es acotada y no es integrable Riemann. Aunque las ideas topológicas subyacentes resultan equivalentes, la función que se define en
este artículo es diferente.
La búsqueda de un procedimiento para medir las discontinuidades de una función, condujo a Hankel (1882) a introducir la noción de
contenido. Posteriores mejoras, debidas entre otros a Jordan (1892),
con los conceptos de contenido interior y contenido exterior, y a Borel
(1898), culminaron con la formulación por parte de Lebesgue de su
teoría de la medida y la integración (1902/1903).
Esta reseña sumaria sirve para destacar la importancia de los interrogantes surgidos del planteo de Riemann en la maduración de las
ideas que llevaron a la gestación del trabajo de Lebesgue, y remarca
el papel que juega la consideración de la perspectiva histórica en la
comprensión del desarrollo de las matemáticas.
2. Un conjunto perfecto, de interior vacío
y medida de Lebesgue positiva
Es conocida la construcción que define al conjunto triádico de
Cantor.
Sea F0 el intervalo [0,1].
Si se le quita el intervalo
, queda:
487
Se elimina ahora el tercio medio de ambos intervalos componentes de F1, y se obtiene:
Continuando iterativamente esta construcción, se obtiene una
sucesión decreciente de conjuntos cerrados:
F0 ⊃ F1 ⊃ F2 ⊃ ............ ⊃ Fn ⊃ ......
donde Fn está constituido por la unión de 2n intervalos cerrados de longitud
.
Su intersección:
, es el triádico de Cantor, y tiene las si-
guientes propiedades:
1) T es no vacío (se prueba que los extremos de los intervalos componentes de cada Fn pertenecen a él).
2) T tiene interior vacío, ya que T ⊂ Fn n, y Fn es unión disjunta de intervalos cerrados de longitud
.
3) T es perfecto (si x ∈ T y B es un entorno de x, existe z ∈ T tal que
z ≠ x y es un extremo de un intervalo componente de algún Fn).
4) T tiene medida cero, porque es el complemento, en el intervalo [0,1],
de un conjunto abierto formado por 1 intervalo de longitud
tervalos de longitud
más:
,.... 2n intervalos de longitud
, 2 in-
,...... y, ade-
.
Es sabido también que si se toma
, y se repite la construcción que generó a T, pero eliminando en cada etapa 2n-1 intervalos de longitud
para obtener Fn, el conjunto
, tiene las
propiedades 1, 2 y 3 del triádico de Cantor, pero su medida de Lebesgue es positiva e igual a 1– α .
Para asegurarse la propiedad 2, es conveniente tomar la siguiente precaución. Si [ak ,bk]es un intervalo componente de Fn–1, el intervalo abierto que se le quita durante la construcción de Fn, puede
elegirse centrado en [ak ,bk]. De esta forma se garantiza que las longitudes de los intervalos componentes de Fn tiendan a cero cuando n
crece indefinidamente.
488
Tanto T como H α tienen la siguiente propiedad:
Lema 1.- Sea A ⊂ [a,b]un conjunto no vacío, perfecto y de interior vacío, y:
donde {In}n∈N es la familia de intervalos abiertos componentes de G .
Supóngase que x ∈ A. Entonces, para todo entorno B de x, existe
un intervalo componente In de G tal que In ⊂ B.
Demostración.- Sea x ∈ A y sea B un entorno de x. Entonces
tal que: (x – ε,x + ε)⊂ B
Como A es perfecto, existe y ∈ A tal que y ≠ x e y ∈(x – ε,x + ε).
Supóngase que x — y. El intervalo (x,y)no está contenido en A, ya que
A tiene interior vacío. Entonces existe z∈ G tal que x — z — y. En consecuencia, existe n tal que zpertenece al intervalo componente In = (an, bn)
de G . Además, ni x ni y pertenecen a G . Entonces:
x ≤ an — z — bn ≤ y
Finalmente: In ⊂[x,y]⊂(x – ε,x + ε)⊂ B.
La prueba es similar si y — x.
3. Una función derivable en todo punto del dominio,
cuya derivada es acotada y no es integrable Riemann
Para la construcción de la función f propuesta en la introducción,
se utilizará la siguiente función auxiliar:
θ:R → R
si |x|— 1
θ(x) = 0
si |x|≥ 1
Como es conocido, esta es una función indefinidamente diferenciable
en los números reales, con lo cual θ y todas sus derivadas son funciones continuas. Además, θ es de soporte compacto y, por ende, lo son
todas sus derivadas. Por lo tanto, θ y sus derivadas son acotadas y alcanzan el máximo y el mínimo en puntos de su soporte. En particular:
0 ≤ θ(x)≤ exp(–1), θ(1) = 0, θ(0) = exp(–1)
y
m ≤ θ´
(x)≤ M , y existen x1,x2 en el intervalo [– 1,1] tales que:
θ(x1)= m ,θ(x2)= M
489
Por cálculo directo se puede verificar que x1 = –x2,m = –M ,x2 ≅ -0,76,
0 ≠ M ≅ 0,8
Sea ahora un intervalo abierto In =(an – δn,an + δn), con δn — 1.
Sea θn : In → R , definida por:
.
Vale que:
Por lo dicho anteriormente, se concluye que las imágenes del intervalo
In para las funciones θn y θ′n resultan: θn(In)=[0, δn2.exp(–1)] ,
θ′n(In)=[m ,M ].
Dado ahora α /0 — α — 1, considérese el conjunto perfecto y de interior vacío Hα construido anteriormente.
Sea
Donde I1,I2,.......In,... son los intervalos componentes de G: In =(an – δn,
an + δn).
Se define la siguiente función:
f:[0,1]→ R
f(x) = 0
si x ∈ H α
f(x)= θn (x)
si x ∈ In ⊂ G
Proposición.a) La función fes derivable para todo x en (0,1), y además existen las derivadas laterales en 0 y 1. La función f′:[0,1] → R es
acotada.
b) f′es continua x ∈ G . f′ es discontinua x ∈ Hα. En consecuencia, f′ es discontinua en un conjunto de medida positiva.
Demostración.- Por definición, f≡ θn en cada intervalo componente In
de G . Como θn es indefinidamente diferenciable en In, y
θ′n(In) = [m, M], resulta findefinidamente diferenciable en G y
f′(G) = [m, M], es decir, f′(G )es un conjunto acotado. En particular, f′
es continua en G .
Se probará ahora que si
, fes derivable en x y vale:
f′(x) = 0
Además, existen las derivadas laterales en los extremos del dominio
y valen:
D + f(0)=0 , D – f(1) = 0
Ello será consecuencia de los dos lemas siguientes.
Lema 2.- Si x ∈ [0,1] e y ∈ H α, se verifica: 0 ≤ f(x)≤(x – y)2
490
Demostración.- La primera desigualdad resulta de la definición de f.
Debe observarse además que la función f sólo es no
nula en el subconjunto de G formado por los intervalos de la forma:
(an – δn2 , an + δn2), donde an es el centro del n-ésimo intervalo componente de G . En el resto de los puntos del intervalo [0,1] vale f(x) = 0,
por lo que, obviamente: f(x)≤ (x – y)2.
Supóngase que x ∈(an – δn2 ,an + δn2)⊂ In =(an – δn ,an + δn), entonces:
f(x)= θn (x) , por lo cual:
f(x)≤ δn2.exp(–1)
(1)
Es evidente que x ≠ y. Supóngase que y — x (si x < y, la prueba es similar a la que sigue).
Vale que: y ≤ an – δn y an – δn2 — x
Luego: x – y ™ (an – δn2)–(an – δn)= δn – δn2
Y:
(δn – δn2)2 <(x – y)2
(2)
Si δn es lo suficientemente pequeño para que :
δn2.exp(–1) ≤(δn – δn2)2
(3)
empleando además (1) y (2), se obtiene:
f(x)≤(x – y)2
Se comprobará ahora que la desigualdad (3) se cumple para los radios δn de los intervalos componentes de G . Vale:
Además:
,
Luego:
,
,
exp(–1)
,
— 1 – 2δn — (1– δn)2
Finalmente: δn2 exp(–1) — δn2 (1– δn)2 =(δn – δn2)2
Esto concluye la prueba del lema 2.
Lema 3.- Sea f: [a,b]→ R . Supóngase que f(x)≥ 0 x ∈[a,b]
. .
Además, sea A ⊂[a,b]y supóngase que, si y ∈ A, se cumple:
f(x)≤(x – y)2
x ∈[a,b]
Entonces:
Si y ≠ b,existe la derivada lateral derecha en y, y vale: D + f(y) = 0
Si y ≠ a,existe la derivada lateral izquierda en y, y vale: D - f(y) = 0
En particular, si
, fes derivable en y, y vale: f′(y) = 0
Demostración.- De las condiciones: 0 ≤ f(x)≤(x – y)2 , se infiere que
f(y)=0, y ∈ A.
Entonces: 0 ≤ f(x)– f(y)≤(x – y)2.
491
Si x ™ y , es decir 0 — x – y, se cumple que:
Luego:
Si x — y , es decir x – y — 0, se cumple que:
Entonces:
Con ambos resultados se obtiene el enunciado.
Esto completa la prueba de que fes derivable en todo punto en
(0,1) y de que existen las derivadas laterales en 0 y 1.
Además, como f′ es acotada en G y vale 0 en H α, es acotada en
[0,1]. Se mostró también que f′ es continua en G . Sólo resta probar que
es discontinua en H α.
Sea x ∈ H α , y sea B un entorno de x.
Por el lema 1, existe un intervalo In , componente de G , tal que In ⊂ B.
Pero, por lo visto anteriormente, existe xn ∈ In tal que:
donde M es una constante positiva.
Entonces, si x ∈ H α, para todo entorno de x, existe z perteneciente a
dicho entorno,tal que f′(z)= M . Como f′(x) = 0, resulta f′ discontinua
en x.
f′resulta entonces discontinua en todo punto de un conjunto de medida positiva, es decir, no es integrable Riemann.
Bibliografía
T. M. Apóstol, Análisis matemático, Editorial Reverté S.A., 1960
A. N. Kolmogorov, S. V. Fomin, Elementos de la teoría de funciones y del
análisis funcional, Editorial MIR, 1975
Norberto Fava, Felipe Zo, Medida e integral de Lebesgue, Red Olímpica, 1996.
J. Rey Pastor, P. Pi Calleja, C. A. Trejo, Análisis matemático, Editorial
Kapelusz, 1952
492
E. W. Hobson, The theory of functions of a real variable and the theory of
Fourier’s series, Cambridge University Press,1907. Versión consultada
a través de Internet en la University of Michigan Historical Math
collection.
Departamento de Ingeniería e Investigaciones Tecnológicas
Universidad Nacional de La Matanza
[email protected]
493