Cap 06 Proyecciones Cartográficas

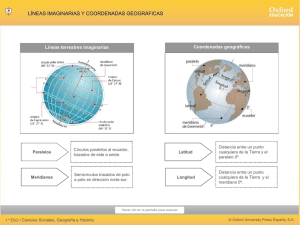
6.
PROYECCIONES CARTOGRÁFICAS
6.1 GENERALIDADES
Nuestra Tierra gira alrededor de su eje una vez cada día. Los dos
puntos extremos de su eje son los polos; el círculo que rodea la Tierra, a
igual distancia de los polos, es el Ecuador. El arco desde cualquiera de los
polos hasta el Ecuador, se divide en 90º. La distancia, expresada en grados, desde el Ecuador a cualquier punto del arco es la latitud de ese punto,
y los círculos de igual latitud son los paralelos. En los mapas es costumbre
señalar los paralelos a distancias uniformes.
El Ecuador se divide en 360º. Los círculos que rodean la Tierra de
polo a polo y pasan por el Ecuador, cortándolo perpendicularmente, sobre
cada uno de los puntos que marcan los grados, se llaman meridianos.
Todos tienen la misma longitud, pero por un convenio internacional se ha
elegido como primer meridiano o meridiano origen, al que pasa por el Observatorio Astronómico de Greenwich, en Londres. La distancia, expresada
en grados, a cualquier punto situado al este o al oeste del primer meridiano, es la longitud de ese punto. Mientras que los círculos que describen los
meridianos tienen todos la misma dimensión, los círculos de los paralelos
van siendo cada vez menores a medida que se acercan a los polos. En
tanto que un grado de longitud mide, en todas partes, desde el ecuador a
los polos, aproximadamente 111,111 kilómetros; un grado de latitud varía
desde aproximadamente 111,111 kilómetros en el Ecuador, hasta 0 km en
lo polos.
Cada grado se divide en 60 minutos y cada minuto en 60 segundos.
Un minuto de latitud mide aproximadamente una milla náutica (1.853
metros).
El mapa es plano, pero la Tierra es casi esférica. Una esfera o una
parte cualquiera de ella, no puede aplanarse sin estirarla o romperla, a
menos que la parte aplastada sea muy pequeña. Presentar en un mapa
la superficie curva de la Tierra no es difícil, si la superficie de que se trata
es de pequeñas dimensiones; pero para hacer los mapas de países, continentes o de la Tierra entera, se necesita lo que se conoce con el nombre
de proyección. Una red de paralelos y meridianos sobre los cuales pueda
dibujarse un mapa representa una proyección cartográfica.
En cualquier proyección, sólo los paralelos o los meridianos o algún
otro grupo de líneas pueden ser verdaderos o exactos, o sea, que representen la misma dimensión que tienen sobre el globo a la escala correspondiente; todas las demás líneas son demasiado largas o demasiado
cortas. Sólo sobre una esfera es posible que los paralelos y los meridianos
sean todos verdaderos. La escala dada en un mapa no puede ser exacta
para todas las partes de ese mapa. La construcción de las diversas proTOPOGRAFÍA
PARA LAS TROPAS
75
yecciones suele empezar con el trazado de los paralelos o de los meridianos que representan las dimensiones exactas.
Un mapa que está dibujado sobre una superficie plana, no representa
en buena forma la superficie de la Tierra. No hay mapa que pueda competir con la esfera en representación precisa de la superficie terrestre. Sin
embargo, un mapa o partes de un mapa pueden mostrar una o más, pero
nunca todas, de las siguientes características: direcciones reales, distancias reales, áreas reales y/o formas reales.
Así, la proyección Mercator es exclusiva en su género. Produce el
único mapa en el que una línea recta dibujada en cualquier parte dentro
de sus límites, muestra una dirección, pero las distancias y áreas quedan
exageradamente distorsionadas cerca de las regiones polares.
En un mapa equidistante, las distancias son reales solamente sobre
líneas particulares, tales como aquellas que radian desde un punto único
seleccionado, como el centro de la proyección. Las formas son normalmente distorsionadas en cada mapa de áreas iguales. Las medidas de las
áreas quedan distorsionadas en mapas conformes, aunque las formas de
áreas pequeñas son mostradas correctamente.
Algunas proyecciones se adaptan para delinear mapas de áreas grandes que son principalmente norte-sur en extensión, otras para áreas grandes que son principalmente este-oeste en extensión y todavía otras para
áreas grandes que son oblicuas al Ecuador.
La escala de un mapa en cualquier proyección es siempre importante
y a menudo decisiva en función de la utilidad del mapa para un propósito
dado. Por ejemplo, la casi grotesca distorsión que es obvia en las altas
latitudes de un mapa Mercator a pequeña escala del mundo, desaparece
casi completamente en un mapa Mercator Transverso a mayor escala, de
un área pequeña en las mismas altas latitudes.
El conocimiento básico de las propiedades de las proyecciones comúnmente usadas ayuda en la elección de un mapa o carta apropiado
para el cumplimiento de una necesidad específica establecida.
Casi todas las proyecciones se elaboran sobre superficies desarrollables,
estas son el plano, el cono y el cilindro, las que pueden localizarse en forma
perpendicular, paralela u oblicua al eje terrestre. Asimismo, todas ellas pueden ser ubicadas en forma tangente o secante a la superficie terrestre.
6.2 DEFORMACIONES
Toda representación plana de una superficie curva altera en mayor
o menor grado sus elementos distancias, ángulos, áreas, etc. Cualquier
sistema de proyección altera toda o parte de la superficie representada;
es así que conociendo las características del mapa a producir se podrá escoger el sistema de proyección más adecuado.
76 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
6.3 CONCEPTOS GENERALES SOBRE PROYECCIONES
Un sistema de proyección permite la representación sobre un plano
de toda o parte de una superficie curva.
Toda proyección trae aparejada la idea de un centro de proyección
y un haz de rayos perspectivos, pero no todas las representaciones son
verdaderas proyecciones.
En general, un sistema de proyección establece una relación biunívoca entre puntos de la superficie a representar y puntos del plano de proyección. Algunas de estas relaciones pueden definir en forma geométrica
un sistema de proyección, pero interesa más definir esa correspondencia
en forma analítica, es decir que a un punto de coordenadas geográficas
conocidas sobre la esfera (o elipsoide) se le puedan calcular las coordenadas planas rectangulares (o polares) correspondientes.
6.4 CLASIFICACIÓN DE LAS PROYECCIONES
Las proyecciones, en general, se clasifican según:
– Superficie sobre la que se proyecta
– Posición de la superficie desarrollable respecto al eje terrestre
– Las deformaciones
– La posición del centro de proyección (azimutales)
6.5 CLASIFICACIÓN DE LAS PROYECCIONES EN FUNCIÓN DE LA
SUPERFICIE SOBRE LA QUE SE PROYECTA
Proyección Cilíndrica, cuando la Tierra se proyecta se proyecta sobre
un cilindro.
Proyección Cónica, cuando la proyección se hace sobre un cono.
Proyección Azimutal, cuando la proyección se hace sobre un plano
(generalmente tangente a la esfera).
Proyección Convencional, cuando la relación entre puntos sobre la
esfera terrestre y puntos del plano se hace en forma puramente analítica, sin intervención de ninguna de las figuras anteriormente mencionadas.
TOPOGRAFÍA
PARA LAS TROPAS
77
PROYECCIONES
6.5.1 PROYECCIÓN CILÍNDRICA
Consideremos un cilindro tangente a la esfera terrestre a lo largo de
un círculo máximo (por ejemplo el Ecuador).
El criterio escogido para definir
el valor de “y” es el
que determina las
características de
la proyección.
Los
planos
meridianos cortan
el cilindro según líneas perpendiculares al Ecuador (generatrices del cilindro).
La proyección de los paralelos puede ser hecha en formas muy diferentes, definiendo una relación y = f (latitud), o bien en forma gráfica
tomando un centro de proyección.
Algunas proyecciones cilíndricas son:
- Proyección Cilíndrica conforme de Mercator (transversal u oblicua)
- Proyección Cilíndrica equivalente de Lambert (transversal u oblicua)
- Proyección Cilíndrica equidistante de Cassini
78 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
6.5.2 PROYECCIÓN CÓNICA
Consideremos un cono tangente a la esfera a lo largo de un paralelo.
Los planos meridianos cortan al cono según generatrices. La proyección
de los paralelos se puede hacer definiendo la distancia radial por medio de
una relación del tipo:
y = f (latitud)
Algunas proyecciones cónicas son:
- Proyección Cónica conforme de Lambert
- Proyección Cónica equivalente de Lambert
- Proyección Cónica equidistante
6.5.3 PROYECCIÓN AZIMUTAL
Se proyecta la esfera sobre un plano tangente a ella en
un punto. La representa la esfera terrestre y un plano tangente en el polo.
Los meridianos están representados por la intersección
de los planos meridianos con el plano sobre el que se hace la proyección.
Los paralelos están representados por círculos concéntricos cuyo radio se puede determinar en función de la latitud mediante una ecuación
del tipo: r = f (latitud).
Algunas proyecciones azimutales son:
- Proyección azimutal conforme (estereográfica, en sus tres variaciones)
- Proyección azimutal equivalente de Lambert
TOPOGRAFÍA
PARA LAS TROPAS
79
6.5.4 PROYECCIÓN CONVENCIONAL
En este tipo de proyección no es posible hacer una representación ya
que del sistema de coordenadas geográficas sobre la esfera se pasa directamente en forma analítica, a un sistema de coordenadas definido sobre
un plano, calculando las coordenadas planas x, y de un punto en función
de su latitud y longitud, sobre la esfera.
6.6 CLASIFICACIÓN DE LAS PROYECCIONES EN FUNCIÓN DE LA
POSICIÓN DE LA SUPERFICIE DESARROLLABLE RESPECTO AL EJE
TERRESTRE
Cuando el eje del cilindro (o cono) coincide con el eje de la Tierra se
habla de proyección normal o polar.
Cuando el eje del cilindro o cono es perpendicular al eje de la Tierra,
la proyección se denomina transversal o ecuatorial.
Cuando el eje del cilindro (o cono) forma un ángulo α, tal que Oº
< α< 90º, se tiene una proyección oblicua.
80 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
Del mismo modo, para el caso de una proyección azimutal se tiene:
- Proyección Polar o normal cuando el plano sobre el que se proyecta es perpendicular al eje de la Tierra
- Proyección Ecuatorial o transversal cuando el plano es perpendicular al plano del Ecuador
- Proyección Oblicua cuando el plano está en posición intermedia
entre la proyección polar y ecuatorial
6.7 CLASIFICACIÓN DE LAS PROYECCIONES EN FUNCIÓN DE LAS
DEFORMACIONES
De acuerdo a este concepto, se pueden definir:
–
–
–
–
Proyecciones
Proyecciones
Proyecciones
Proyecciones
Conformes
Equivalentes o Equiáreas
Afilácticas
Equidistantes
6.7.1 PROYECCIONES CONFORMES
Proyecciones Conformes son aquellas que conservan los ángulos y
por lo tanto conservan también la forma de figuras infinitesimales.
Ejemplos:
- Proyección Cilíndrica conforme de Mercator, en sus tres casos:
normal, transversal y oblicua
- Proyección Cónica conforme de Lambert, en sus tres situaciones:
normal, transversal y oblicua
- Proyección Estereográfica
6.7.2 PROYECCIONES EQUIVALENTES
Proyección equivalente es aquella que conserva las áreas (es decir la
escala superficial).
TOPOGRAFÍA
PARA LAS TROPAS
81
Ejemplos:
- Proyección Cilíndrica equivalente de Lambert (normal, transversal)
- Proyección Cónica equivalente de Lambert (normal)
- Proyección Bonne
6.7.3 PROYECCIONES AFILÁCTICAS
Se incluyen en esta categoría aquellas proyecciones que no son ni
conformes ni equiáreas.
6.7.4 PROYECCIONES EQUIDISTANTES
Son aquellas que mantienen equidistancia entre los paralelos y ortogonalidad entre éstos y los meridianos.
Ejemplo:
- Proyección Cónica de “De L’Isle”
6.8 CLASIFICACIÓN DE LAS PROYECCIONES SEGÚN LA POSICIÓN DEL
CENTRO DE PROYECCIÓN (AZIMUTALES)
De acuerdo a esta clasificación, las proyecciones se pueden agrupar en:
- Proyección Perspectiva
- Proyección Cuasi Perspectiva
- Proyección Seudo Perspectiva
6.8.1 PROYECCIÓN PERSPECTIVA
p
m
M
C
82 TOPOGRAFÍA PARA LAS TROPAS
Se define así una proyección en
la que dado el “punto de vista” “o”, la
perpendicular por este punto al plano sobre el que se hace la proyección pasa además por el centro de la
esfera.
Lo que caracteriza las proyecciones perspectivas es la distancia
del “punto de vista” “o”, al centro de
la esfera “c”.
PROYECCIONES CARTOGRÁFICAS
De acuerdo al punto de vista, la proyección perspectiva se divide en:
6.8.2 PROYECCIÓN GNOMÓNICA O CENTROGRÁFICA
Cuando el punto de vista coincide con el centro de la esfera.
6.8.3 PROYECCIÓN ESTEREOGRÁFICA
Cuando el centro de proyección se encuentra sobre la esfera en la
antípoda del punto de contacto de la esfera con el plano de proyección.
6.8.4 PROYECCIÓN ORTOGRÁFICA O PARALELA
En el que el punto “o” se encuentra en el infinito y todos los rayos
son paralelos.
6.9 PROYECCIONES CUASI PERSPECTIVAS
Se incluyen en este grupo aquellas cuya distancia del punto “o” al
centro de la esfera tiene un valor comprendido entre infinito y el valor del
radio de la esfera terrestre.
Estas también reciben el nombre
de escenográficas.
TOPOGRAFÍA
PARA LAS TROPAS
83
6.10 PROYECCIONES PSEUDO PERSPECTIVAS
En este tipo de proyección la perpendicular bajada desde el punto de
vista al plano sobre el que se proyecta, no pasa por el centro de la esfera.
(Varía la orientación del punto de vista).
Según la orientación del punto de vista se pueden clasificar estas
proyecciones en tres grandes grupos:
6.10.1 PROYECCIÓN POLAR
Cuando el plano de proyección es perpendicular al eje de la Tierra (p.
ej. tangente en el polo) y la dirección de proyección es paralela al eje de
la Tierra.
Polar
6.10.2 POYECCIÓN MERIDIANA
Si el plano de proyección es perpendicular al plano ecuatorial y la
dirección es perpendicular a dicho plano.
Meridiana
6.10.3 PROYECCIÓN CENITAL
Cuando el plano es tangente en uno de los polos la dirección de proyección es oblicua.
Cenital
84 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
GRÁFICO RESUMEN DE PROYECCIONES
Cilíndrica
Cónica
Azimutal o Cenital
Posición Normal
Posición Transversal
Posición Oblicua
Tangente
Secante
6.11 CARACTERÍSTICAS DE ALGUNAS PROYECCIONES
6.11.1 LA ESFERA
ESPECIFICACIONES
Las direcciones, las distancias, las formas y las áreas representadas
sobre la esfera son reales y acorde a la escala de representación.
TOPOGRAFÍA
PARA LAS TROPAS
85
GRANDES CÍRCULOS
La distancia más corta entre dos puntos cualquiera, sobre la superficie terrestre, puede ser encontrada rápidamente y en forma fácil por un
gran círculo.
CARACTERÍSTICAS
Aún el más grande globo posee una escala muy pequeña y muestra
relativamente poco detalle. Es costoso para reproducir y actualizar. Difícil
para trasladar. Voluminoso para almacenar.
En la esfera los paralelos se ven como tales y equidistantes entre sí.
Los meridianos y otros arcos de grandes círculos son líneas rectas (si se
contemplan en forma perpendicular a la superficie de la Tierra). Los meridianos convergen hacia los polos y divergen hacia el Ecuador.
Los meridianos están equidistantes a la altura de cada paralelo, pero
su distancia entre sí disminuye progresivamente desde el Ecuador a los
polos. En el Ecuador los meridianos están a la misma distancia que los
paralelos entre sí y a los 60º de
latitud están a la mitad de la distancia que los paralelos. Los paralelos y meridianos se cortan en
ángulos rectos.
El área de la superficie limitada por cualquiera de dos paralelos y dos meridianos (para una
distancia dada), es la misma en
cualquier lugar entre los mismos
dos paralelos.
El factor escala en cada punto es el mismo en cualquier dirección.
6.11.2 PROYECCIÓN DE MOLLWEIDE
Los meridianos son elipses
trazadas a distancias uniformes;
los paralelos son líneas horizontales espaciadas de modo
que cada faja de latitud tenga
la misma superficie que en el
globo. Esta proyección es muy
utilizada para el trazado de planisferios, especialmente en los
atlas europeos.
86 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
6.11.3 PROYECCIÓN DE ECKERT
Son análogas a la sinusoidal o a la de Mollweide, pero
los polos se indican como una
línea cuya largo es la mitad del
correspondiente al Ecuador en
la proyección. Hay diversas
variantes; los meridianos son
curvas sinu-soidales o elipses;
los paralelos son horizontales
y equidistantes o de tal modo
que se obtenga una proyección de áreas iguales. Su uso en el trazado de
planisferios va en aumento. La figura muestra la variante elíptica de áreas
iguales.
6.11.4 PROYECCIÓN DE BONNE
Los paralelos se trazan
exactamente como en la proyección cónica. Todos los paralelos están divididos exactamente y las curvas que los
atraviesan son los meridianos.
Es una proyección de áreas
iguales. Se emplea para los
mapas de los continentes septentrionales: Asia, Europa y
América del Norte.
6.11.5 PROYECCIONES AZIMUTALES
En este grupo se proyecta una parte del globo desde un punto de
vista sobre un plano. El punto de vista puede estar a diferentes distancias,
obteniéndose así diferentes proyecciones. El plano de proyección puede
ser tangente al Ecuador, a un polo o a cualquier otro punto sobre el que
se desee enfocar la atención. La cualidad más importante de todas las
proyecciones azimutales es que muestran cada punto en su verdadera
dirección (azimut), con respecto al punto que sirve de centro (punto céntrico), y todos los puntos igualmente distantes del punto céntrico, también
estarán igualmente distantes en el mapa.
TOPOGRAFÍA
PARA LAS TROPAS
87
6.11.6 PROYECCIÓN AZIMUTAL EQUIDISTANTE
Esta es la única proyección en que cada punto se muestra tanto en la
verdadera dirección del gran círculo, como a la distancia exacta del punto
céntrico, pero todas las demás direcciones y distancias están deformadas.
El principio de esta proyección puede comprenderse mejor estudiando su
aplicación polar. En la mayor parte de los mapas polares se emplea esta
proyección. La aplicación oblicua se usa para determinar la posición por
radio, en las investigaciones sismológicas y en los vuelos a larga distancia.
Hay que hacer un mapa separado para cada punto central
elegido.
Las distancias y direcciones hacia todas las posiciones
son reales solamente desde el
punto central de proyección.
Las distancias son correctas
entre puntos a lo largo de líneas rectas que pasen a través
del centro, todas las demás
distancias están incorrectas.
Cualquier línea recta dibujada
a través del centro está sobre
un círculo mayor.
La distorsión de áreas y
formas aumenta al alejarse del
punto céntrico.
6.11.7 PROYECCIÓN AZIMUTAL EQUIÁREA DE LAMBERT
Adecuada para regiones que se extienden en todas direcciones, desde un punto central, tales como Asia y el océano Pacífico.
Las áreas en el mapa son representadas en exacta proporción a las
mismas áreas en la Tierra. Los cuadrángulos (limitados por dos meridianos y dos paralelos), en la misma latitud son uniformes en área.
Las direcciones son reales solamente desde el centro. La escala disminuye gradualmente desde ese punto y la distorsión de formas aumenta
al alejarse del centro. Cualquier línea recta dibujada a través del punto
central está sobre un círculo mayor.
El mapa es equiárea, pero no conforme, perspectivo o equidistante.
Permite obtener un buen mapa polar y a menudo se extiende hasta
incluir los continentes del hemisferio sur. Es la proyección que se emplea
más comúnmente para el trazado de los mapas del hemisferio oriental y el
88 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
occidental y es, también, muy útil para
el de los continentes, porque presenta
áreas proporcionadas
que, relativamente,
tienen poca deformación.
6.11.8 PROYECCIÓN TRANSVERSAL DE MERCATOR
Usada para mapas a diferentes escalas; tales mapas pueden ser unidos en sus bordes solamente si están en la misma zona con respecto a un
meridiano central. También usada para delinear mapas de áreas grandes
que son principalmente norte-sur en extensión.
Las distancias son reales solamente a lo largo del meridiano central
elegido por el cartógrafo o en otro caso a lo largo de dos líneas paralelas
a él, pero todas las distancias, direcciones, formas y áreas son exactas
dentro de los límites de los 15º del meridiano central. La distorsión de
distancias, direcciones y tamaño de las áreas aumenta rápidamente fuera de la banda de los 15º. Esto se debe a que el mapa es conforme, sin
embargo, las formas y ángulos dentro de los límites de cualquier área
pequeña (tales como aquellas mostradas por un mapa topográfico), son
esencialmente reales.
El espacio de cuadrícula aumenta desde el meridiano central. El Ecuador es recto. Otros paralelos son curvas complejas cóncavas con respecto
al polo más cercano.
El meridiano central y cada meridiano a 90º desde él, son rectos y
otros meridianos son curvas complejas cóncavas con respecto al meridiano central.
TOPOGRAFÍA
PARA LAS TROPAS
89
6.11.9 PROYECCIÓN MERCATOR
Usada para la navegación o para mapas de regiones ecuatoriales.
Cualquier línea recta sobre estos mapas es una línea loxodrómica (línea
de dirección constante).
Las direcciones a lo largo de una línea loxodrómica son reales entre
dos puntos cualquiera en un mapa, pero una línea loxodrómica usualmente no es la distancia más corta entre puntos.
Las distancias son reales solamente a lo largo del Ecuador, pero son
razonablemente correctas hasta los 15º desde el Ecuador. Pueden ser usadas escalas especiales para medir distancias con otros paralelos.
Las áreas y formas de espacios grandes aparecen distorsionadas. La
distorsión aumenta alejándose del Ecuador y es extrema en las regiones
polares. El mapa, sin embargo, es conforme en los ángulos y forma dentro
de cualquier área pequeña (tales como aquellas mostradas por un mapa
topográfico), son esencialmente reales.
El mapa no es perspectivo, de áreas iguales o equidistantes.
El Ecuador y otros paralelos son líneas rectas (el espacio entre ellos
aumenta hacia los polos), y se cortan con los meridianos (igualmente líneas rectas espaciadas),
en
ángulos rectos.
Los polos
no se observan
en ésta proyección, pues quedan fuera del
área proyectada.
6.11.10 PROYECCIÓN OBLICUA DE MERCATOR
Usada para mostrar regiones a lo largo de un círculo mayor distinto al
Ecuador o a un meridiano, esto es, teniendo su extensión general oblicua
al Ecuador. Este tipo de mapa puede ser hecho para mostrar como una
línea recta, la distancia más corta entre cualquier par de puntos preseleccionados a lo largo del círculo mayor elegido.
Las distancias son reales solamente a lo largo del círculo mayor (la
línea de tangencia para esta proyección), o a largo de dos líneas paralelas
a él. Las distancias, direcciones, áreas y formas son exactas dentro de los
límites de los 15º del círculo mayor.
La distorsión de distancias, áreas y formas aumenta desde el círculo
mayor. Es excesiva con respecto a los bordes de un mapa del mundo, ex90 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
cepto cerca de la senda del círculo mayor.
El mapa es conforme, pero no perspectivo, de áreas iguales o equidistante. Las líneas loxodrómicas son curvadas.
El espacio de cuadrícula aumenta desde el círculo mayor, pero la
conformidad se mantiene. Ambos polos pueden
ser mostrados. El Ecuador
y otros paralelos son curvas complejas cóncavas
con respecto al polo más
cercano. Dos meridianos
apartados en 180º son líneas rectas. Todos los demás son curvas complejas
cóncavas con respecto al
círculo mayor.
6.11.11 PROYECCIÓN MERCATOR DE ESPACIO OBLICUO
Esta proyección conforme de la era espacial fue desarrollada para ser
usada en imágenes Landsat, porque no hay distorsión a lo largo del territorio rastreado bajo el satélite. Tal como se necesita para el mapeo continuo de imágenes de satélite, pero es útil solamente para una relativamente angosta banda a lo largo
del territorio rastreado.
Los mapas Mercator
de espacio oblicuo muestran un territorio rastreado
por el satélite, como una
línea curvada que es continuamente real para la escala a medida que la órbita
continúa.
La extensión del mapa
está definida por la órbita
del satélite.
El mapa es básicamente conforme, especialmente en la región de
“scaneo” del satélite.
6.11.12 PROYECCIÓN CILÍNDRICA DE MILLER
Usada para representar la Tierra en una estructura rectangular. Popular para mapas del mundo. Parecida a la Mercator pero no es útil para
TOPOGRAFÍA
PARA LAS TROPAS
91
la navegación. Muestra los
polos como líneas rectas.
Evita algunas de las
exageraciones de escala de
la Mercator, pero aparecen
formas y áreas con distorsión.
Las direcciones y distancias son reales solamente a lo largo del Ecuador.
La distorsión de distancias,
áreas y formas es extrema en latitudes altas. El mapa no es equiárea,
equidistante, conforme o perspectivo.
6.11.13 PROYECCIÓN DE ROBINSON
Usa más coordenadas tabulares que fórmulas matemáticas para hacer que el mundo “luzca bien”.
Tiene mejor equilibrio entre tamaño y forma para tierras de alta latitud, que las proyecciones Mercator, Van der Grinten o Mollweide. La Unión
Soviética, Canadá y Groenlandia aparecen fieles a su tamaño, aunque
Groenlandia se observa comprimida.
Las direcciones son reales a lo largo de todos los paralelos y a lo largo
del meridiano central. Las distancias son constantes a lo largo del Ecuador y otros paralelos, pero las escalas varían. La escala es real a lo largo
de los paralelos 38º N y S, y es constante a lo largo de cualquier paralelo
dado; idénticos paralelos N y S, a lo largo, están a igual distancia desde
el Ecuador.
Todos los puntos tienen algo de distorsión. Muy baja a lo largo del
Ecuador y dentro de los límites de 45º del centro. La
más grande cerca de los polos.
No es conforme, equiárea, equidistante o perspectivo.
6.11.14 PROYECCIÓN SINUSOIDAL EQUIÁREA (SANSON - FLAMSTEED)
Usada frecuentemente en atlas para mostrar modelos de distribución,
también es frecuentemente utilizada para mostrar áreas de prospección
de hidrocarburos y cuencas sedimentarias del mundo.
Una proyección equiárea de fácil dibujo para mapas del mundo. Pue92 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
de tener un meridiano central único o, en forma interrumpida, diversos
meridianos centrales. El espacio de cuadrícula retiene la propiedad de
equivalencia de área. Las áreas en el mapa son proporcionales a las mismas áreas en el mapa.
Las distancias son correctas a lo largo de todos los paralelos y el (los)
meridiano(s) central(es). Las formas son distorsionadas en forma creciente lejos del(os) meridiano(s) central(es) y cerca de los polos. El mapa no
es conforme, perspectivo o equidistante.
Esta proyección no permite trazar planisferios aceptables porque las
regiones exteriores quedan
deformadas, pero la porción
central es buena, por lo que
esta parte de la proyección
se usa a menudo en los mapas de África y América del
Sur.
6.11.15 PROYECCIÓN ORTOGRÁFICA
Usada para vistas perspectivas de la Tierra, la Luna y otros planetas. La
Tierra aparece como lo haría en una fotografía desde el espacio profundo.
Las direcciones son reales solamente desde el punto de centro de la
proyección. La escala disminuye a lo largo de todas las líneas radiantes
desde el punto centro. Cualquier línea recta a través del punto centro es
un círculo mayor. Las áreas y formas están distorsionadas por la perspectiva; la distorsión aumenta desde el punto centro.
El mapa es perspectivo pero no conforme o equiárea. En el aspecto
polar, las distancias son reales a lo largo del Ecuador y todos los otros
paralelos.
Esta proyección fue conocida para los egipcios y griegos, hace ya
2.000 años.
La aplicación polar o la ecuatorial son raras, pero la oblicua se ha
popularizado debido a su visualidad.
Tiene la apariencia de una esfera terráquea. Aunque la deformación en la
periferia es extremada, no nos damos
cuenta de ella porque el ojo percibe
la proyección no como un mapa, sino
como la representación de un globo
en sus tres dimensiones. Es evidente
que sólo puede representarse un hemisferio (la mitad del globo).
TOPOGRAFÍA
PARA LAS TROPAS
93
6.11.16 PROYECCIÓN ESTEREOGRÁFICA
Usada para mapas árticos y
antárticos. Puede ser usada para
cartografiar áreas grandes o de
extensión continental o similar en
todas direcciones.
Usada en geofísica para resolver problemas de geometría
esférica.
La proyección de las áreas
polares es usada para mapas topográficos y cartas de navegación
en latitudes sobre 80º.
Las direcciones son reales
solamente desde el centro de la
proyección. La escala aumenta desde el centro. Cualquier línea recta a
través del punto centro, es un círculo mayor. La distorsión de áreas y de
grandes formas aumenta desde el centro.
El mapa es conforme y perspectivo pero no equiárea o equidistante.
Azimutal. Geométricamente proyectado en un plano. El punto de proyección está en la superficie del globo opuesta al punto de tangencia.
Data desde el siglo 2 A.C. y es atribuida a Hiparco.
6.11.17 PROYECCIÓN GNOMÓNICA
Usada junto con la Mercator, por algunos navegantes para encontrar
la senda más corta entre dos puntos. También usada en trabajos
sísmico, porque las ondas tienen
tendencia a viajar a lo largo de círculos mayores.
Cualquier línea recta dibujada en el mapa está sobre un círculo mayor, pero las direcciones
son reales solamente desde el
punto central de la proyección. La
escala aumenta muy rápidamente desde el centro. La distorsión
de las formas y áreas también
aumenta desde el centro.
El mapa es perspectivo (desde el centro de la Tierra en un plano tangente), pero no conforme, equiárea o equidistante.
94 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
No obstante la proyección tiene una cualidad importante: todos los
círculos máximos aparecen como líneas rectas. Por esta razón se usa para
trazar las rutas de los vuelos a larga distancia o para la navegación transoceánica.
6.11.18 PROYECCIÓN CÓNICA
La idea original de la Proyección Cónica es la de poner sobre el globo
un cono en el cual se proyectan los paralelos y los meridianos desde el
centro del globo. Luego se abre el cono y se extiende sobre un plano. El
cono puede hacerse tangente a cualquier paralelo central que se elija.
La Proyección Cónica realmente usada, es una modificación de esta
idea. El radio del paralelo central se obtiene como se indica en el dibujo.
Los meridianos son líneas rectas radiales exactamente espaciadas que
cortan el paralelo central. Los paralelos son círculos concéntricos espaciados a distancias exactas. Todos los paralelos son demasiados largos,
excepto el central.
La proyección se usa para el trazado de mapas de países en latitudes
medias, pues presenta la configuración y los accidentes geográficos con
pequeños errores de escala. Hay diversas variantes. El uso de dos paralelos centrales, uno cerca de la parte superior del mapa, el otro cerca de la
parte inferior, permite reducir el error de escala.
6.11.19 PROYECCIÓN CÓNICA EQUIÁREA DE ALBERS
En la Proyección de Albers los paralelos están espaciados desigualmente, para hacer que la proyección sea de áreas iguales.
Está bien adaptada para países grandes u otras áreas que son principalmente de extensión este-oeste y que requieren una representación de
igual área. Esta es una proyección adecuada para los mapas de Estados
Unidos. Se usa para muchos mapas temáticos.
Los mapas que muestran áreas adyacentes pueden ser unidos por
sus bordes solamente si tienen los mismos paralelos estándares (paralelos
sin distorsión) y la misma escala.
Todas las áreas en
el mapa son proporcionales a las mismas áreas
sobre la Tierra. Las direcciones son razonablemente fieles en regiones
limitadas. Las distancias
son reales en ambos paTOPOGRAFÍA
PARA LAS TROPAS
95
ralelos estándares. La escala es real solamente a lo largo de los paralelos
estándares.
6.11.20 PROYECCIÓN CÓNICA CONFORME DE LAMBERT
En ésta proyección los paralelos están espaciados de tal manera que
cualquier pequeño rectángulo de la red, tenga las mismas formas que en
el globo. Esta es la mejor proyección para las cartas de navegación aérea,
pues tiene azimutes relativamente rectos. Usada para mostrar países o
regiones que se extienden principalmente en forma este-oeste.
Es una de las proyecciones más usadas en Estados Unidos hoy día. Es
parecida a la Cónica de Albers pero el espacio de cuadrícula difiere.
Retiene la conformidad. Las distancias son reales solamente a lo largo de los paralelos estándares; son razonablemente fieles en otras partes
pero en regiones limitadas.
La distorsión de áreas y formas es mínima, pero aumenta a partir de los paralelos estándares. Las formas
en mapas a gran escala de
áreas pequeñas son reales
en general.
El mapa es conforme, pero no es perspectivo,
equiárea ni equidistante.
6.11.21 PROYECCIÓN CÓNICA EQUIDISTANTE (CÓNICA SIMPLE)
Usada en atlas para mostrar áreas en latitudes medias.
Apropiada para mostrar regiones dentro de unos pocos grados de
latitud y que están ubicadas sobre un lado del Ecuador.
Las distancias son reales solamente a lo largo de todos los meridianos y a lo largo de uno o dos
paralelos estándares. Las direcciones, formas y áreas son
razonablemente fieles, pero la
distorsión aumenta a partir de
los paralelos estándares.
El mapa no es conforme,
perspectivo ni equiárea, pero es
un arreglo entre la Cónica Conforme de Lambert y la Cónica
Equiárea de Albers.
96 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
6.11.22 PROYECCIÓN POLICÓNICA
El meridiano central divide exactamente la Tierra en dos puntos; los
paralelos son círculos no concéntricos, cuyos radios se obtienen trazando
tangentes al globo, tal como si éste estuviera cubierto por varios conos en
lugar de uno solo. Cada paralelo se divide con exactitud y las curvas que
los atraviesan son los meridianos. Todos los meridianos, excepto el central, son demasiado largos. Esta proyección se usa para el trazado de cartas topográficas a gran escala
y, con menos frecuencia, para
el de los países o continentes,
caso este último, en que es
apropiada para áreas con una
orientación norte-sur.
Las direcciones son reales
solamente a lo largo del meridiano central y en las distancias
a lo largo de cada paralelo. La
distorsión aumenta a partir del
meridiano central.
6.11.23 PROYECCIÓN CÓNICA CONFORME OBLICUA BIPOLAR
Esta proyección, “hecha a la medida”, es usada para mostrar parcial
o totalmente el continente americano. Los contornos en el diagrama de
la proyección representan áreas mostradas en los mapas tectónicos y de
basamento de Norteamérica.
La escala es real a lo largo de dos líneas (“paralelos normales transformados”), que no están trazadas a lo largo de ningún meridiano o paralelo. La escala está comprimida entre estas líneas y extendida más allá de
ellas. La escala generalmente está bien pero el error es de un 10% en el
borde de la proyección usada.
El espacio de cuadrícula aumenta a partir de las
líneas de la escala real pero
mantiene las propiedades de
conformidad, excepto para
una desviación pequeña en
donde las dos proyecciones
cónicas se unen.
El mapa es conforme
pero no equiárea, equidistante o perspectivo.
TOPOGRAFÍA
PARA LAS TROPAS
97
6.11.24 PROYECCIÓN UNIVERSAL TRANSVERSAL DE MERCATOR (UTM)
La idea era tener una proyección universal que abarcara toda la Tierra y se adaptara en la mejor forma a cada área.
La solución fue dividir la Tierra en husos y generar un sistema de
tablas de conversión universal. Las primeras ecuaciones referidas al elipsoide para representarlo en un plano fueron establecidas por Gauss y las
ecuaciones de transformación de coordenadas geográficas en rectangulares fueron resueltas por Krugger.
Se conoce así la proyección Gauss-Krugger, pero los países de habla
inglesa la denominaron sistema transverso de Mercator, siendo de esta
forma como se ha mantenido.
La proyección transversal de Mercator es un sistema de representación conforme de la esfera o elipsoide de revolución y corresponde al desarrollo de un cilindro tangente a la Tierra a lo largo del Ecuador. El sistema
de Gauss difiere en el sentido que corresponde al desarrollo de un cilindro
tangente a la Tierra a lo largo de un meridiano.
El sistema internacional está basado en los husos definidos por Gauss
a lo largo del Ecuador y se denomina proyección Universal Transversal de
Mercator (UTM).
Esta proyección posee ciertas características generales que le otorgan su calidad de proyección universal, tales como:
- Es una proyección geodésica y su aplicación se encuentra en mapas o cartas a escala grande y media
- Se origina siempre a partir de un elipsoide exactamente definido
- Su cáneva se basa en coordenadas geodésicas, mientras que otras
proyecciones cartográficas se basan en coordenadas geográficas
- Las coordenadas rectangulares E y N son calculadas para cada
punto geodésico y estos puntos se establecen sobre el elipsoide
por coordenadas geográficas
- La transformación de las coordenadas esféricas o elipsoidales sobre un plano es imposible realizarla sin alguna distorsión, sin embargo, en esta proyección geodésica se reduce al mínimo tal dificultad, encontrándose la mayor similitud con la realidad
Esta proyección alcanzó su mayor importancia después de la Segunda Guerra Mundial. Los países de la Organización de del Atlántico Norte
(OTAN) establecieron una posición para los mapas militares de los distintos Estados partícipes, ya que la existencia de coordenadas no comparables y de distintos elipsoides había generado una serie de problemas. Así,
la proyección se basó en el Elipsoide Internacional de 1924 aprobado por
la Unión Geodésica y Geográfica Internacional.
98 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
Aunque la proyección es transversal, sin embargo es especial, porque
sobre el cilindro envolvente sólo es proyectada una pequeña zona, la cual
está definida por un huso. Para proyectar otra zona, el cilindro es girado
en el sentido de la longitud hacia esta otra zona.
Para los efectos de esta proyección, la Tierra se ha dividido en husos
de 6º de longitud, y se extiende desde los 84º de latitud norte hasta los
80º de latitud sur. Cada huso tiene un meridiano central, el cual a su vez
es el meridiano de tangencia.
Esta proyección es conforme y no tiene centro de proyección. En ella
el Ecuador y el meridiano central se representan como una línea recta y
los meridianos son levemente curvados al igual que los paralelos con el
objeto de mantener la conformidad.
P.N.
84°
ECUADOR
80°
P.S.
HUSO = 6° Longuitud
En la figura siguiente se muestra al cilindro envolviendo la Tierra y
visto desde el punto de vista imaginario sobre el polo. En forma exagerada
se muestra entre A y B y entre C y D una zona de 6º de longitud. El cilindro
está secante para disminuir las distorsiones, y en los puntos 1, 2, 3 y 4 no
existe distorsión. Los puntos 5-6 representan el meridiano central.
Las partes encerradas por los puntos 1-5, 5-2, 3-6 y 6-4 se reducen
en tamaño en la proyección, y las partes encerradas por los puntos A-1,
B-2, C-3 y D-4 crecen en tamaño.
Existen dos líneas rectas que son grandes círculos: el Ecuador y el
meridiano central, que son perpendiculares entre sí.
Estas dos líneas constituyen los ejes de la cuadrícula en la proyección
UTM en cada zona
TOPOGRAFÍA
PARA LAS TROPAS
99
6.11.25 OTRAS PROYECCIONES
5
1
2
B
A
6˚
Polo
6˚
D
C
Gnomónica sobre cubo
circunscrito oblicuo
Eckert II (meridianos rectos)
100 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
Gnomónica sobre Icosaedro Regular
P.N.
P.S.
Polo Norte
Polo Sur
Planisferio Hammer
Van der Griten (Policónica)
TOPOGRAFÍA
PARA LAS TROPAS
101
Sinusoidal Oblicua
Proyección de Peters
Policónica
Planisferio Aitoff
102 TOPOGRAFÍA PARA LAS TROPAS
TOPOGRAFÍA
Cilíndrica
Cilíndrica
MERCATOR
TRANSVERSAL
MERCATOR
ESPACIAL
Cilíndrica
MERCATOR
Cilíndrica
Esfera
GLOBO
MERCATOR
OBLICUA
Tipo
Proyección
Hemisferio
Perspectiva
Direcciones verdaderas
Equidistante
Equiárea
Empleo
Continente
Propiedades
Uso
Geológico
= Cumple
= Parcial
Temático
Conforme
RESUMEN DE LAS PROYECCIONES
Propiedades, Nivel de Empleo y Uso
Clasificación de acuerdo a su tipo
PROYECCIONES CARTOGRÁFICAS
PARA LAS TROPAS
103
Navegación
Presentaciones
Topográfico
Escala Grande
Escala Media
Región
Mundial
Rumbos
Convencional
104 TOPOGRAFÍA PARA LAS TROPAS
Pseudo
Cilíndrica
Azimutal
Azimutal
Azimutal
Azimutal
SINUSOIDAL
EQUIÁREA
ORTOGRÁFICA
ESTEREOGRAFÍA
GNOMÓNICA
AZIMUTAL
EQUIDISTANTE
Cónica
Cónica
Azimutal
Pseudo
Cilíndrica
ROBINSON
AZIMUTAL
EQUIÁREA
LAMBERT
CÓNICA
EQUIÁREA
ALBERTS
CÓNICA
CONFORME
LAMBERT
Cilíndrica
MILLER
CILÍNDRICA
Cónica
Cónica
Cónica
CÓNICA
EQUIDISTANTE
CÓNICA
SIMPLE
POLICÓNICA
BIPOLAR
OBLICUA
CÓNICA
CONFORME
PROYECCIONES CARTOGRÁFICAS
TOPOGRAFÍA
PARA LAS TROPAS
105
6.12 GLOSARIO
6.12.1 AZIMUT
Es una dirección de círculo máximo medida en el sentido en que
giran los punteros del reloj, partiendo del norte. Una dirección de círculo
máximo apunta hacia un lugar a lo largo de la línea más corta sobre la
superficie de la Tierra. Esta dirección no es la misma que la de la brújula.
El centro de un círculo máximo es el centro de la esfera.
También se puede expresar como el ángulo medido en grados entre
una línea base radiando desde un punto céntrico y otra línea radiando
desde el mismo punto. Normalmente, la línea base apunta al norte y los
grados son medidos en la dirección de giro de los punteros del reloj, desde
la línea de base.
6.12.2 ASPECTO
Las proyecciones de un mapa azimutal están divididas en tres aspectos: el aspecto polar, con tangencia en un polo; el ecuatorial, con tangencia en el ecuador; el oblicuo, con tangencia en cualquier punto distinto de
los aspectos anteriores. (La palabra “aspecto”, ha reemplazado al vocablo
“caso” en la literatura cartográfica moderna.
6.12.3 CONFORMIDAD
Una proyección es conforme cuando en cualquier punto de ella, la
escala es la misma en toda dirección. Por lo tanto, los meridianos y paralelos se intersectan en ángulo recto y las formas de áreas muy pequeñas
y ángulos con lados muy cortos se mantienen. El tamaño de la mayoría de
las áreas, sin embargo, es distorsionado.
6.12.4 CUADRÍCULA
Es la red imaginaria que conforma el sistema coordenado esférico
basado en líneas de latitud y longitud.
6.12.5 CÍRCULO MAYOR
Es un círculo formado sobre la superficie de una esfera por una línea
que pasa a través de su centro. El Ecuador, cada meridiano y algunas circunferencias completas de la Tierra, forman un círculo mayor. El arco de
un círculo mayor muestra la distancia más corta entre dos puntos de la
superficie terrestre.
106 TOPOGRAFÍA PARA LAS TROPAS
PROYECCIONES CARTOGRÁFICAS
6.12.5 ESCALA LINEAL
Es la relación entre una distancia sobre el mapa y la correspondiente
distancia sobre la superficie terrestre.
En algunos casos la escala varía de un punto a otro en el mismo
mapa. El grado de variación está en relación directa con la proyección utilizada para el mapa.
6.12.6 EQUIÁREA
Una proyección es equiárea, si cada parte, al igual que la totalidad,
tiene la misma relación del área representada con la parte correspondiente sobre la tierra, a la escala respectiva.
Ningún plano, carta o mapa, puede ser simultáneamente equiárea y
conforme.
6.12.7 EQUIDISTANTE
Los mapas equidistantes muestran las direcciones reales solamente
desde el centro de la proyección o a lo largo de un conjunto especial de
líneas.
Ningún plano, carta o mapa, puede ser simultáneamente equiárea y
equidistante.
6.12.8 PROYECCIÓN
Es una representación sistemática de un cuerpo esférico, tal como la
Tierra, sobre una superficie plana.
Cada proyección tiene propiedades específicas que la hacen útil para
propósitos determinados.
6.12.9 LINEA LOXODRÓMICA (O DE RUMBO)
Es una línea sobre la superficie de la Tierra que corta todos los meridianos por los cuales pasa, en un mismo ángulo. Una línea loxodrómica
muestra la dirección real.
Los paralelos y meridianos, los cuales también mantienen constantes
direcciones reales, pueden ser considerados aspectos especiales de líneas
loxodrómicas.
Una línea loxodrómica es una línea recta en una proyección Mercator.
Una línea loxodrómica recta no muestra la dirección más corta entre
dos puntos, a menos que éstos se encuentren localizados en el Ecuador o
en el mismo meridiano.
TOPOGRAFÍA
PARA LAS TROPAS
107
BL