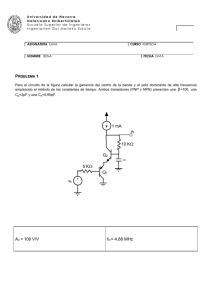
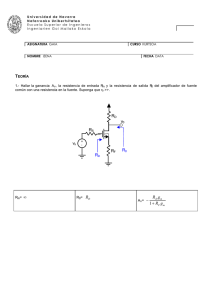
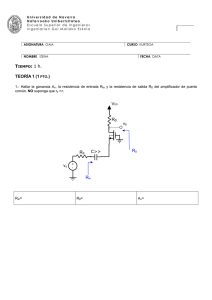
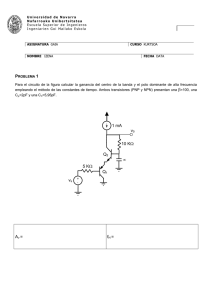
TEORÍA (30 % de la nota) 1.

Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
TERMODINÁMICA (Troncal, 7,5 cr.)
NOMBRE IZENA
TEORÍA
CURSO KURTSOA
2º
FECHA DATA
8/02/03
(30 % de la nota)
Tiempo máximo: 60 minutos
Utilice la última hoja como borrador
1.
(a) Diagrama temperatura-entropía de una sustancia pura. Dibujar claramente la posición de la
curva de saturación, punto crítico, y tres líneas de presión constante: P1<Pc , P2=Pc y P3>Pc.
(b) Demostrar que en el diagrama T-s las líneas de presión constante en la zona de vapores sobrecalentados responden aproximadamente a una ecuación exponencial, del tipo T=A eS/cp+B.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
2.
Un gas perfecto de calor específico cp se expande en una turbina reversible con un caudal m& según un proceso politrópico de exponente politrópico n, desde P1 y T1 hasta P2. Calcular la potencia
producida por la turbina, en función únicamente de las variables citadas.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
3.
(a) Deducir la ecuación de Gibbs o relación fundamental, que combina la Primera y la Segunda Ley
de la Termodinámica.
(b) Demostrar que la variación de entropía de m kg de un gas perfecto durante un proceso reversible a volumen constante viene dada por
S 2 − S 1 = mc v ln
T2
T1
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
4.
Indique esquemáticamente los componentes de una bomba de calor que opera según un ciclo
teórico de Carnot invertido.
Explique razonadamente qué modificaciones son necesarias en los componentes del ciclo teórico
de Carnot invertido, para cambiarlo a un ciclo práctico de bomba de calor por compresión de vapor.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
TERMODINÁMICA (Troncal, 7,5 cr.)
CURSO KURTSOA
2º
NOMBRE IZENA
FECHA DATA
8/02/03
Tiempo máximo para los problemas: 3 horas.
Utilice la última hoja como borrador.
PROBLEMA 1 (25 % de la nota)
En un cilindro como el de la figura hay 0,8 kg de R-12 a –20 °C. El R-12 se encuentra cubierto por
un pistón deslizante y adiabático, de peso y espesor despreciables, situado inicialmente a z1 = 0,4
m de altura. Encima del pistón hay cierta cantidad de una sustancia líquida semejante al mercurio,
de densidad desconocida. El cilindro tiene un rebosadero situado a L = 0,8 m de altura.
Se aporta calor lentamente al cilindro por su parte inferior, de modo que la tapa empieza a ascender y el líquido superior empieza a rebosar. El proceso termina cuando la tapa alcanza la altura del
rebosadero y se ha vertido todo el líquido.
A=0,1 m2
L=0,8 m
R-12
0,8 kg
–20 °C
z1=0,4 m
Q
(a) Representar el proceso en un diagrama P-v.
(b) Calcular la densidad del líquido [kg/m3].
(c) Calcular la temperatura y el título del vapor en el estado final.
(d) Calcular el calor aportado [kJ].
Datos: presión atmosférica P0 = 100 kPa, aceleración de la gravedad g = 9,81 m/s2.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
TERMODINÁMICA (Troncal, 7,5 cr.)
CURSO KURTSOA
2º
NOMBRE IZENA
FECHA DATA
8/02/03
PROBLEMA 2 (25 % de la nota)
Utilice la última hoja como borrador.
En un cohete la propulsión se realiza con hidrógeno y oxígeno puros. Ambas sustancias entran en
estado gaseoso en la cámara de combustión adiabática a 10 bar y 25 °C. Los gases de salida (3)
salen de la cámara a 2500 °C y 10 bar, y a velocidad despreciable. A continuación se expanden en
una tobera adiabática reversible hasta la presión de salida de 1 bar (4).
H2
O2
1
Cámara de combustión
3
2
4
Tobera
(a) Representar el proceso en un diagrama T-s.
(b) Calcular el porcentaje de exceso de oxígeno empleado.
(c) Calcular la velocidad de salida de los gases de combustión [m/s].
(d) Al ganar altura el cohete, la presión atmosférica es cada vez más baja. La velocidad de los gases de escape (4), ¿será mayor, menor o igual que a nivel del mar? Justificar la respuesta.
Datos: suponer comportamiento de gas perfecto, con calores específicos cp(O2)=cp(H2)=3,5R;
cp(H2O)=4,5R. Suponer que los gases de escape se comportan como si fueran O2 puro.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
TERMODINÁMICA (Troncal, 7,5 cr.)
CURSO KURTSOA
2º
NOMBRE IZENA
FECHA DATA
8/02/03
PROBLEMA 3 (25 % de la nota)
Utilice la última hoja como borrador.
Se considera un ciclo de Rankine regenerativo con dos calentadores de agua de alimentación, uno
abierto y el otro cerrado. El vapor entra en la turbina a 12,5 MPa y 550 °C, y sale hacia el condensador a 10 kPa. Se extrae vapor de la turbina a 0,8 MPa para el calentador cerrado, y a 0,3 MPa
para el abierto. El agua de alimentación a caldera (9) se calienta en el calentador cerrado hasta la
temperatura de condensación del vapor extraído (2). El vapor extraído abandona el calentador
cerrado como líquido saturado, y a continuación se estrangula hacia el calentador abierto. La salida del condensador (5) y del calentador abierto (7) y cerrado (10) son líquidos saturados.
La eficiencia isoentrópica de turbina y bombas es del 85 %. La potencia neta del ciclo es de 250
MW.
1
Turbina
y
2
Caldera
z
1–y–z
4
3
8
9
B2
Calent.
cerrado
7 Calent.
10
abierto
11
Condensador
6
B1
5
(a) Representar el diagrama T-s del ciclo.
(b) Calcular las fracciones de vapor extraído de la turbina, y y z.
(c) Calcular el caudal de vapor que debe circular por la caldera [kg/s].
(d) Calcular el rendimiento del ciclo [%].
Datos: propiedades de algunos estados:
Estado
1
2
3
4
P [kPa]
12500
800
300
10
T [°C]
550
h [kJ/kg]
3474,3
2862,3
2712,4
2305,8
s [kJ/kgK]
6,6300
x [%]
99,43
88,34