Julio04

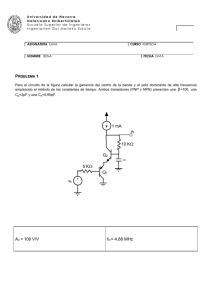
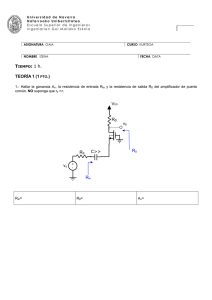
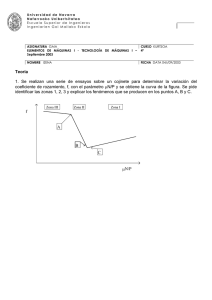
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
CURSO KURTSOA 2º
FUNDAMENTOS DE CIENCIA DE MATERIALES
NOMBRE IZENA
FECHA DATA 08-JULIO-2004
Problema 1
Se quiere diseñar un sistema para frenar unas vagonetas de 300 kg de masa (ver figura (a)). Se sabe que
las vagonetas se mueven a una velocidad de 36 km/h. Para frenar las vagonetas, éstas impactan con una
pieza de goma cuya respuesta mecánica a compresión viene dada por la figura (b). La pieza de goma tiene
un área transversal de 0,03 m2 y su longitud en reposo de 0,20 m. Por razones de seguridad, la goma no
ha de superar una deformación de 0,5.
(a)
(b)
σn
15 MPa
0
0,5
εn
a) ¿Será capaz la goma de frenar la vagoneta de forma segura?
b) ¿Cuál es la masa máxima de la vagoneta que viajando a 36 km/h puede detener el sistema de forma
segura, esto es, sin deformar la goma más de 0.5?
c) ¿Que fuerza máxima soportan los tornillos que fijan el sistema de frenado al suelo cuando este detiene
la vagoneta cuya masa ha sido calculada en el apartado b) que avanza a 36 km/h?
NOTA: Considerar que para este problema las curvas tensión-deformación reales e ingenieriles
coinciden y que el área transversal de la goma permanece constante durante la deformación.
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
CURSO KURTSOA
2º
FUNDAMENTOS DE CIENCIA DE MATERIALES
NOMBRE IZENA
FECHA DATA 08-JULIO-2004
Disponen de 2 horas para la realización de esta parte del examen.
Problema 2
La presión dentro de un avión Airbus A380 es siempre constante e igual a 0,8 atm (~0,08 MPa) gracias a
los sistemas de presurización. Cuando el avión está en tierra, la presión atmosférica es de 1,0 atm.,
mientras que a la altitud máxima de vuelo (~10.000 metros) la presión atmosférica es de 0,2 atm. El
fuselaje del avión se puede aproximar a un cilindro de diámetro de 7 m, con un espesor de pared de
3 mm.
(a) Demostrar que las tensiones a las que está sometida la pared del fuselaje debido a la presión
relativa P en el interior del avión vienen dadas por:
σθ =
PR
PR
en dirección circuferencial, y σ z =
, en dirección longitudinal.
t
2t
donde R es el radio y t el espesor de la pared.
(b) Despreciando las tensiones en el fuselaje debido al peso propio del avión, calcular la dirección y
magnitud de la tensión tractiva máxima a la que está sometido el fuselaje durante el vuelo. ¿Cuál
es el valor de esta tensión cuando el avión está en tierra?
(c) Durante el último aterrizaje del avión, una piedra ha golpeado la pared del avión, produciendo una
grieta superficial de longitud 1,0 mm (ver figura). Determinar el número de vuelos que puede
realizar el avión antes de que dicha grieta crezca hasta producir un agujero en el fuselaje.
(d) Explicar en qué consiste el criterio de diseño de “fuga antes que rotura”. De acuerdo con este
criterio, ¿está diseñado el avión de forma segura?
Datos: El fuselaje está fabricado de una aleación de Al-Cu con las siguientes propiedades:
σy= 200 MPa
Kc=25 MPa m
Ecuación de Paris:
dc
= 2 ⋅ 10 −10 ∆K 3 (con σ en MPa y c en m)
dN
D=7 m
t =3 mm
Grieta superficial
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA
CURSO KURTSOA 2º
FUNDAMENTOS DE CIENCIA DE MATERIALES
NOMBRE IZENA
FECHA DATA 08-JULIO-2004
Problema 3
Un acero que ha sido enfriado lentamente presenta a una temperatura justo por debajo de la temperatura
eutectoide una microestructura constituida por 25% de ferrita proeutectoide y 75% de perlita en peso.
Calcular:
(a) El contenido en C (en % en peso) de dicho acero
(b) 1 kg de dicho acero se calienta hasta 1600ºC y se mezcla con la cantidad necesaria de cementita
para convertirlo en un acero eutectoide. ¿Cuál es la cantidad de cementita necesaria?
Tras la mezcla, el acero eutectoide se enfría lentamente hasta temperatura ambiente. Dibujar
esquemáticamente la microestructura e indicar los porcentajes en peso de cada fase que presentará este
acero eutectoide a temperaturas de:
(c) Justo por encima de la temperatura eutectoide
(d) Justo por debajo de la temperatura eutectoide
Por último, comentar cualitativamente qué diferencias cabría esperar en la microestructura y las
propiedades mecánicas (límite elástico y tenacidad) del acero, si en vez de enfriarlo lentamente, se enfría
según las curvas de enfriamiento indicadas en la curva TTT del acero (v. figura adjunta):
(e) La curva 1 indica un enfriamiento rápido hasta una temperatura media y luego un mantenimiento
(f) La curva 2 corresponde a un temple (enfriamiento rápido) hasta temperatura ambiente
Curva TTT del acero
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Estola
ASIGNATURA GAIA
CURSO KURTSOA
2º
FUNDAMENTOS DE CIENCIA DE MATERIALES
NOMBRE IZENA
FECHA DATA 08-JULIO-2004