Variables aleatorias - Facultad de Ingeniería

Variables aleatorias
M. en A. Víctor D. Pinilla Morán
Facultad de Ingeniería, UNAM
Resumen
El concepto de variable aleatoria como abstracción de un
evento aleatorio y su definición.
variable aleatoria discreta: función de probabilidad, sus
propiedades y su representación gráfica.
Variable aleatoria continua: función de densidad, sus
propiedades y su representación gráfica.
Valor esperado o esperanza matemática de la variable aleatoria
discreta y de la continua y su interpretación práctica. El valor
esperado como operador matemático y sus propiedades.
Momentos con respecto al origen y a la media. Función
generatriz de momentos de la variable aleatoria discreta y de la
continua.
Parámetros de las distribuciones de las variables aleatorias
discretas y continuas. Medidas de tendencia central: la media,
la mediana y la moda. Medidas de dispersión: el rango y
aplanamiento. La varianza como el segundo momento con
respecto a la media y sus propiedades.
3.1 El concepto de variable aleatoria
como abstracción de un evento aleatorio
y su definición.
Es posible incorporar el uso de
herramientas matemáticas al cálculo de
probabilidades a través de realizar una
operación consistente en buscar una regla
de correspondencia que proyecte los
resultados de un evento o experimento en la
recta de los reales.
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
45
Al asociar los resultados aleatorios a puntos
sobre la recta de los reales, es decir, a la
variable independiente, esta variable
adquiere un carácter aleatorio. De tal forma,
se le denomina variable aleatoria.
De acuerdo a la naturaleza del evento,
existen dos tipos de variables aleatorias:
φ
φ
Se dice que una variable aleatoria X
es discreta si el número de valores
que puede tomar es contable (ya sea
finito e infinito) y si estos pueden
arreglarse en una secuencia que
corresponde con los enteros
positivos.
Se dice que una variable aleatoria X
es continua si sus valores consisten
en uno o más intervalos de la recta
de los reales.
Definir a la
variable aleatoria
y su naturaleza
discreta o
continua.
Algunos
autores
denominan a
todo el
proceso con
el nombre de
Distribución de
Probabilidad
Asignar valores
en la recta de
los reales al
espacio
muestral
A la regla de correspondencia f(x) se le
denomina función de probabilidad, siempre
y cuando cumpla con una condición que se
describirá más adelante.
El proceso integral de creación de una
variable aleatoria y su respectiva función de
probabilidad puede describirse en el
siguiente diagrama a bloques:
Como comentario a este procedimiento, la
asignación de valores en la recta de los
reales para cada punto del experimento o
del espacio muestral se hace de acuerdo a la
experiencia del diseñador del experimento,
no existe una regla escrita para hacerlo. No
obstante se recomienda asignarle valores
que sean representativos del experimento en
ánimo de clasificar el experimento.
Definir el
espacio
muestral del
experimento
Algunos autores
denominan a este
paso en el proceso
En forma
gráfica
Analítica
Asignar
probabilidades
Definir f(x)
Por otra parte, un término muy importante
dentro de la probabilidad y la Estadística es
el de Distribución1.
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
46
Distribución.
(Del lat.distributio,-onis).
1.
f. Acción y efecto de distribuir.
2.
f.Com. Reparto de un producto a los
locales en que debe comercializarse.
3.
f.Econ. Asignación del valor del
producto entre los distintos factores
de la producción.
4.
f.Mat. Función que representa las
probabilidades que definen una
variable aleatoria o un fenómeno
aleatorio.
5.
f. Ret. Figura, especie de
enumeración, en que
ordenadamente se afirma o niega
algo acerca de cada una de las cosas
enumeradas.
De acuerdo a la anterior definición, el
bloque del proceso que implica la acción de
asignar la probabilidad a cada uno de los
valores que puede adquirir la variable
aleatoria es denominado por varios autores
como distribución de probabilidad, aunque
otros autores consideran como distribución
de probabilidad a todo el proceso.
3.2 Variable aleatoria discreta: Función
de probabilidad, sus propiedades y su
representación gráfica. Función de
distribución
acumulativa,
sus
propiedades y su representación gráfica.
Ejemplifiquemos
aleatorio.
a partir de un evento
Determinar la distribución de probabilidad
para un experimento que consiste en lanzar
simultáneamente 2 dados no cargados y
contabilizar la suma de los números
visibles.
Probabilidad y Estadística
Noviembre 2009
Paso 1. La variable aleatoria que denote
este experimento tendrá naturaleza discreta,
en virtud de que cada uno de los resultados
es claramente distinguible y se define como
la suma de los números visibles de ambos
dados.
La variable aleatoria discreta X se define
como la suma de las caras visibles de
ambos dados.
Paso 2. Definir el espacio muestral.
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,6)
(3,6)
(5,5)
(6,5)
(6,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(6,2)
(6,3)
(6,4)
(5,6)
(2,2)
(3,2)
(4,2)
(5,2)
(4,4)
(5,4)
(4,6)
(2,3)
(2,4) (3,3)
(2,5) (4,3) (3,4)
(3,5) (5,3)
(4,5)
Paso 3. Asignación de valores en la recta de
los reales. En virtud de que el valor
asignado debe ser representativo del
experimento, se le asignará a cada evento la
suma de las caras visibles.
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,6)
(3,6)
(5,5)
(6,5)
(6,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(6,2)
(6,3)
(6,4)
(5,6)
Espacio
Muestral
X
(2,2)
(3,2)
(4,2)
(5,2)
(4,4)
(5,4)
(4,6)
2
3
4
5
6
7
8
9
10
11
12
(2,3)
(2,4)
(2,5)
(3,5)
(4,5)
(3,3)
(4,3)
(5,3)
(3,4)
M.A. Víctor Damián Pinilla Morán.
47
Paso 4. Asignación de probabilidades. En
este caso se hace bajo el criterio clásico:
DISCRETO
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,6)
(3,6)
(5,5)
(6,5)
(6,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(6,2)
(6,3)
(6,4)
(5,6)
X
Px (X)
2
3
(2,2)
4
(3,2) (2,3)
5
(4,2) (2,4) (3,3)
6
(5,2) (2,5) (4,3) (3,4) 7
(4,4) (3,5) (5,3)
8
(5,4) (4,5)
9
(4,6)
10
11
12
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
Paso 5. Definir la función de probabilidad.
Puede hacerse de tres formas, tabular, como
se ve en la tabla anterior, gráfica:
En general una variable aleatoria discreta
representa los resultados de un espacio
muestral en forma tal que
P( X = x )
Se entenderá la probabilidad de X tome el
valor de x de esta forma, al considerar los
valores de una variable aleatoria es posible
desarrollar una función matemática que
asigne una probabilidad a cada realización x
de la variable aleatoria X, esta función
recibe el nombre de función e probabilidad
(función masa de probabilidad) de la
variable aleatoria X.
Por axiomas de probabilidad se tiene:
0.2
Px ( X )
dice entonces que X es una variable
aleatoria.
0.15
1)
0.1
2)
0.05
Px (X = x) ≥ 0
∑ P (X ) = 1
∀x
x
0
0
5
10
15
Función de distribución acumulativa. Se
define a la función de distribución
acumulada de la variable aleatoria como la
probabilidad de que x sea menor o igual a
un valor específico de x.
X
Y en forma analítica.
P(X)=
6− 7− X
36
0
F(x) es la función de distribución acumulada
F(x) ≡ P( X ≤ x) = ∑ Px ( X i )
X=2,3,4,...12.
otros casos
Por axiomas de probabilidad.
Variable aleatoria discreta. Sea S un
espacio muestral sobre el que se encuentra
definida una función de probabilidad. Sea X
una función de valor real, definida sobre S
de manera que transforme los resultados de
S en punto sobre la recta de los reales, se
Probabilidad y Estadística
Noviembre 2009
X
i
≤ x
La función de distribución acumulada
representa la suma de las probabilidades
puntuales hasta el valor de x de X inclusive.
P (0) = P ( x ≤ 0) = 0
P (4) = P ( x ≤ 4) =
6
36
M.A. Víctor Damián Pinilla Morán.
48
Puesto que el área total bajo Fx(x) es 1, la
probabilidad del intervalo a ≤ x ≤ b , es el
área acotada por la función de densidad y
las rectas x=a y x=b.
En general la función de distribución
acumulativa
P(x) de una variable
aleatoria discreta es una función no
decreciente de los valores de X de tal
manera que:
Va riable Alea toria Continua
1) 0 ≤ P( x) ≤ 1
2) P ( X > x) = 1 − P ( X < x)
3) P ( xi) ≥ P( xj ) , si xi ≥ xj
∫
b
a
F X ( x )dx
f(x)
P (a ≤ x ≤ b ) =
3.3 Variable aleatoria continua: Función
de densidad, sus propiedades y su
representación gráfica. Función de
distribución
acumulativa,
sus
propiedades y su representación gráfica.
Dada la naturaleza continua del espacio
muestral, resulta imposible determinar el
valor preciso que exactamente toma una
variable; por este motivo, para fenómenos
continuos resulta más apropiado visualizar
probabilidades en intervalos.
En el caso discreto se asignan
probabilidades positivas a todos los valores
puntuales de la variable aleatoria, pero la
suma de todas ellas es 1, aún a pesar de que
el conjunto de valores sea infinito contable.
Para el caso continuo lo anterior no es
posible, por esta razón la probabilidad de
que una variable aleatoria continua X tome
un valor específico x es cero (0).
La distribución de probabilidad de una
variable aleatoria continua X está
caracterizada por una función, llamada
función de densidad o probabilidad. Esta
función no es la misma que para el caso
discreto. Dado que existe que la
probabilidad de que X tome el valor
específico x es cero, esta función determina
la probabilidad en un intervalo.
P(a ≤ x ≤ b ) =
∫ F (x )dx
b
a
a
x
b
Función de distribución Acumulativa.-La
distribución acumulativa F(x) es una
función lisa no decreciente de los valores de
la variable aleatoria con las siguientes
propiedades:
F (− ∞ ) = 0
F (∞ ) = 1
P(a ⟨ x⟨b ) = F (b ) − F (a )
d
F ( x) = Fx ( x)
dx
Al igual que en el caso de una v.a. discreta
la función de distribución acumulativa de
una variable aleatoria continua X es la
probabilidad de que X tome un valor
menor o igual a algún x específico.
x
P ( X ≤ x) = F ( x) = ∫ f (t )dt
−∞
en donde t es una variable artificial de
invariación, por lo tanto la función de
distribución acumulativa es: el área acotada
por la función de densidad que se encuentra
a la izquierda de la recta X=x.
X
Para cualquiera a y b.
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
49
Ejercicio. La variable aleatoria X está dada
por:
−x
ke 2 , x⟩ 0
Fx(x)=
0, otros casos
Determinar el valor de k, la función de
distribución acumulativa, la probabilidad de
que 2<x<6 y la probabilidad de que
x ≤ 8 .Si:
∫
∞
−∞
Fx ( x)dx = 1
entonces:
3.4 Valor esperado o media de la variable
aleatoria discreta y de la continua, y su
interpretación
práctica.
El
valor
esperado como operador matemático y
sus propiedades. Momentos con respecto
al origen y a la media.
Valor esperado. El valor esperado nace de
la práctica de los juegos de azar. El valor
esperado (o esperanza) representa para los
jugadores la cantidad que ganarán, o
perderán, después de jugar repetidamente
cierto juego.
La esperanza o valor esperado debe
interpretarse como un promedio. Imagínese
que un experimento, por ejemplo, un
volado, se repite un número grande de
veces; algunos volados se ganan, otros se
pierden. La pregunta que se hace el jugador
es: Después de la jornada de juego ¿Cuánto
espero haber ganado?
Otra interpretación consiste en denominar
al valor esperado como un promedio
ponderado. A diferencia del promedio
aritmético, el promedio ponderado toma en
cuenta la existencia de los elementos
además de su valor a promediar. Obsérvese
el siguiente ejemplo:
En una tienda de autoservicio se expenden
botellas de vino. En un primer embarque, se
ponen a la venta 60 botellas de las cuales se
venden 35, quedando en existencia 25 a un
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
50
precio de $150.00. Posteriormente, el
proveedor surte 15 botellas más en un
segundo embarque, con la salvedad de que
el costo de cada botella aumentó a $200.00.
El contador de la tienda debe pagar
impuesto sobre inventarios a razón de 10%
por el valor de los activos. La pregunta es:
¿cómo debe calcular el precio de las
botellas para pagar el menor impuesto
posible?
El contador tiene tres opciones:
1. Pagar el impuesto correspondiente por
cada botella de acuerdo con su costo. Este
es un caso ideal debido a que cuando las
botellas se ponen a la venta no se hace
diferencia de las botellas pertenecientes al
embarque uno que las pertenecientes al
embarque dos. No obstante, este resultado
será el resultado ideal.
Impuesto = [(25botellas x $150.00)
+ (15 botellas x $200.00)] x 10%
Impuesto = $ 675.00
Esta cantidad debería pagar el contador de
ser posible la diferenciación en los
elementos de los embarques.
2. Pagar el impuesto correspondiente con
base en el promedio aritmético de los
precios de las botellas.
Para este caso el precio será:
X =
$150.00 x$200.00
= $175.00
2
Impuesto = (40 botellas x $175.00) x 10%
= $ 700.00
Impuesto = (40 Botellas x $168.75) x 10%
= $ 675.00
Este resultado coincide con el caso ideal y
no requiere de diferenciar los precios de las
botellas de acuerdo con el embarque al que
pertenecen.
Puede observarse que el promedio
ponderado considera la cantidad de
elementos además del valor de cada uno de
ellos. Por tal motivo, se considera al
promedio ponderado una cantidad más
representativa que el promedio aritmético.
Este mismo concepto se aplica a la
probabilidad. El valor esperado es el
resultado promedio de una serie de eventos
(valores de una variable aleatoria),
considerando la probabilidad de cada uno
de ellos.
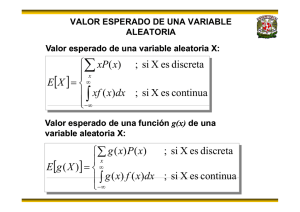
Definición: El valor esperado de una
variable aleatoria se define como:
E{ X } = ∑ xPx ( x)
γx
para una V.A. Discreta
∞
E{ X } =
∫ xf
x
( x)dx
−∞
para una V.A. Continua
En general, es posible obtener el valor
esperado de una función g(x):
E{ X } = ∑ g ( x) Px ( x)
γx
para una V.A. Discreta
3. Pagar el impuesto con base en el
promedio ponderado de los precios de las
botellas.
E{ X } =
Para este caso el precio será:
para una V.A. Continua
X =
( 25)($150 .00) + (15)($200 .00)
= $168.75
40
Probabilidad y Estadística
Noviembre 2009
∞
∫ g ( x) f
x
( x)dx
−∞
donde g(x) es una función de la variable
aleatoria X.
M.A. Víctor Damián Pinilla Morán.
51
Es necesario aclarar que el valor esperado
es una constante y es una propiedad de la
distribución de probabilidad de la variable
aleatoria X.
El valor esperado de una variable aleatoria
continua puede ser interpretado como la
abscisa del centroide de la figura formada
por la función Fx(x) junto con el eje x (y
los extremos de Fx(x) si los hubiera).
Propiedades.
Primera propiedad:
E{c} = c donde c ≡ cte
Demostración:
∞
∞
−∞
−∞
∫ cf x ( x)d = c ∫ f x ( x)dx = c(1) = c
Segunda propiedad:
E{aX + b} = aE{ X } + b
donde a, b ≡ ctes
Demostración:
Momentos de la variable aleatoria. Son
los valores esperados de ciertas funciones
de x; que forman una colección de medidas
descriptivas que pueden emplearse para
caracterizar la distribución de probabilidad
de x y especificarlo si todos los momentos
de x son conocidos.
A pesar de que los momentos de x pueden
definirse alrededor de cualquier punto de
referencia, generalmente se definen
alrededor del cero o del valor esperado de
x.
Momentos de orden “n” con respecto al
origen. Se definen como la esperanza
matemática de h( x ) = X n y se representan
μn ' .
Tercera propiedad:
E{g ( x) + h( x)} = E{g ( x)} + E{h( x)}
⎧ ∑ X n Px ( X )
⎪⎪ γx
μ n ´= ⎨ ∞
n
⎪ ∫ X f x ( X )dx
⎪⎩−∞
V.A. Discreta
V.A. Continua
Momento cero con respecto al origen:
μ ' 0 = E{ x 0 } = 1
E{g ( x) + h( x)} = E{g ( x)} + E{h( x)}
De los tres anteriores resultados se
desprende que el valor esperado es un
operador lineal.
El valor esperado de una variable aleatoria
discreta puede ser interpretado como el
centro de masa Px(xi) colocadas en los
puntos xi del eje x.
Probabilidad y Estadística
Noviembre 2009
Primer momento con respecto al origen:
⎧∑ xPx ( x)
⎪⎪ γx
μ '1 = E{x} = ⎨ b
⎪∫ x f x ( x)dx
⎪⎩ a
M.A. Víctor Damián Pinilla Morán.
52
Al primer momento alrededor del cero se le
conoce como media o valor esperado de la
distribución y se denota: μ '1 = μ x = E{x}
Segundo
origen:
momento
con
respecto
al
⎧∑ x 2 Px ( x)
⎪⎪ γx
μ ' 2 = E{x 2 } = ⎨ b
⎪∫ x 2 f x ( x) dx
⎪⎩ a
De la misma forma se obtienen momentos
con respecto al origen de orden superior.
Momentos con respecto a la media. Se
definen como la esperanza matemática de
g ( X ) = ( X − μ x ) n y se representan por
μn .
V.A. Discreta
V.A. Continua
Momento cero con respecto a la media:
{
Para el caso discreto
}
μ 0 = E ( X − μ x )0 = E{1} = 1
Primer momento con respecto a la
media:
⎧∑ ( X − μ x ) Px ( x)
⎪⎪ γx
μ1 = E{( X − μ x )} = ⎨ b
⎪∫ ( X − μ x ) f x ( x)dx
⎪⎩ a
Segundo momento con respecto a la
media:
⎧∑ ( X − μ x ) 2 Px ( x)
⎪⎪ γx
μ 2 = E{( X − μ x ) 2 } = ⎨ b
⎪∫ ( X − μ x ) 2 f x ( X ) dx
⎪⎩ a
Al segundo momento con respecto a la
media se le conoce como variancia ó
varianza y se denota por σ 2 ó σ x2 . La
varianza de una variable aleatoria es una
medida de dispersión de la distribución de
probabilidades de ésta. Por ejemplo, para el
caso continuo, si la mayor parte del área por
debajo de la curva de distribución se
encuentra cercana a la media, la varianza es
pequeña; si la mayor parte del área se
encuentra muy dispersa al rededor de la
media, la varianza es grande.
A la raíz cuadrada positiva de la varianza
recibe el nombre de desviación estándar y
se denota por σ.
Si se desea comparar la varianza con la
desviación estándar de varias variables con
diferentes unidades entre sí, la comparación
resultará injusta debido a que las
distribuciones de variables aleatorias con
unidades pequeñas tendrán aparentemente
menos variación. Para hacer este tipo de
comparaciones se define otro indicador
denominado coeficiente de variación: como
el cociente de la desviación estándar entre
la media y la desviación estándar tiene las
mismas unidades que el coeficiente de
variación por lo tanto es adimensional.
Cv =
Probabilidad y Estadística
Noviembre 2009
σ
μx
M.A. Víctor Damián Pinilla Morán.
53
Momentos de orden superior. Como en el
caso de la varianza, cualquier momento de
la variable aleatoria con respecto de la
media puede expresarse en términos de esta
misma y de momentos alrededor del cero.
Expresando en función de la media y
momentos:
μ 3 = μ 3' − 3μ x μ 2' + 2μ x3
Aplicando el binomio de Newton:
r
(x − μ x )r = ∑ (−1) i
i =0
r!
(μ x ) i x r −i
(r − i )!i!
Para obtener la fórmula de los momentos
aplico el valor esperado:
Binomio de Newton
(a + b )r = ∑ (− 1)i r! a r −i b i
(r − i )i!
r
3.5 Parámetros de las distribuciones de
las variables aleatorias discretas y
continuas. Medidas de tendencia central:
media, mediana y moda. Medidas de
dispersión: rango, desviación estándar,
variancia y coeficiente de variación.
Medida de simetría. La variancia como el
segundo momento con respecto a la
media y sus propiedades.
Medidas descriptivas. Estos índices
permiten caracterizar a las distribuciones de
frecuencias para poder hacer una
interpretación acertada de la misma.
i =0
⎧r
⎫
r!
x r −i μ i ⎬
E ( x − μ ) r = E ⎨∑ (−1)
(r − i )!i!
⎩ i =O
⎭
r
r!
= ∑ (−1)
μ i E x r −i
(r − i )!i!
i =0
{
}
{ }
{ }= μ
ri
μμ
E {( x − μ ) } = ∑ (−1)
(r − i )!i!
si
Ex
r −i
1
r −i
r
r
i
i =o
1
r −i
Medidas de Tendencia Central. Son
aquellas medidas que nos proporcionan un
dato que, con ciertos matices, puede
considerarse representante de los n datos
obtenidos del muestreo.
Media. Tradicionalmente se considera a la
media como un promedio aritmético de n
datos. En realidad es más que esto. La
media pretende representar de la mejor
forma a los datos de los cuales proviene.
Para calcular el tercer momento respecto a
la media:
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
54
Esta representación puede lograrse de
varias formas.
Media Aritmética
n
X =
∑X
i =1
i
n
donde n es el número total de datos.
Como dato representante de una muestra, la
media aritmética presenta el problema de
los datos ubicados en los extremos de la
muestra, los más pequeños y los más
grandes, que en la generalidad suelen ser
pocos, sesgan o inducen un error en el
resultado. La media aritmética nunca debe
utilizarse por sí sola para hacer alguna
conclusión sobre la muestra, resulta
conveniente acompañarla de alguna medida
de dispersión como se verá más adelante.
Media Ponderada. A diferencia del
promedio
aritmético,
el
promedio
ponderado toma en cuenta la existencia de
los elementos además de su valor a
promediar.
Probabilidad y Estadística
Noviembre 2009
Es decir, al tomar en cuenta el número de
elementos repetidos minimiza la posibilidad
de uno o dos datos extremos modifiquen
dramáticamente el resultado. La media
ponderada corresponde directamente al
valor esperado o esperanza matemática
estudiada en Probabilidad.
Media geométrica.
X = n X 1 ⋅ X 2 ⋅ X 3 ⋅ ... ⋅ X n
En la práctica suele obtenerse a través de
logaritmos.
Media armónica. La media armónica de
una serie de números es el recíproco de la
media aritmética de los recíprocos de los
números.
X=
1
n
= n
1 n 1
1
∑
∑
n i =1 X i
i =1 n
M.A. Víctor Damián Pinilla Morán.
55
en la práctica se utiliza:
1
n
1
=
X
∑X
i =1
i
n
Mediana. Es el dato que divide
exactamente a la mitad a la muestra.
n impar
n par
Para su cálculo como dato agrupado, la
mediana se obtiene determinando cual es la
clase que incluye a la mediana, la cual se
distingue porque tiene una frecuencia
acumulada relativa mayor o igual a 0.5
(50% de los datos).
F ( X ) = 0.5
Moda. Es el elemento de la muestra que
más se repite. Una muestra puede tener una
o más modas. Cuando todos los elementos
de la muestra son diferentes, no tiene
sentido hablar de ella.
En forma gráfica, la moda se observa en el
máximo de la curva, de tal forma que su
obtención se logra con las herramientas que
el cálculo diferencial proporciona para
obtener el máximo de una función.
Medidas de dispersión. Estas medidas
reflejan la separación o alejamiento de los
elementos de una muestra. Estas medidas
deben acompañar a las medidas de
tendencia central, particularmente a la
media, para evitar los efectos que los datos
extremos tienen sobre ellas.
La medida de dispersión más sencilla es el
Rango, amplitud o recorrido, que como
ya se mencionó es la diferencia entre el dato
mayor y del menor.
Probabilidad y Estadística
Noviembre 2009
Varianza.
Tal y como la define la
probabilidad, la varianza de una variable
aleatoria es el segundo momento de la
misma con respecto a la media. Asimismo,
se interpreta de la misma forma, como un
promedio de las distancias de cada dato
hacia la media.
Desviación estándar. Es fácil de percibir, a
partir de un análisis dimensional, que la
varianza posee las unidades de la variable
muestreada elevada al cuadrado. Esta
situación
no
permite
una
rápida
visualización o interpretación de la
dispersión de los datos.
En virtud de lo anterior, la desviación
estándar es la raíz cuadrada de la varianza:
σ = σ2
La desviación estándar también es conocida
como desviación típica o error estándar.
Desviación media. Ciertos autores opinan
que para obtener el promedio de las
distancias de cada dato con respecto a la
media debe obtenerse el valor absoluto de
la distancia entre ambos puntos y después
obtenerse su promedio. De tal forma, la
desviación media se define como:
n
Desviación Media =
∑X
i =1
−X
i
n
Asimismo, algunos autores utilizan como
referencia a la mediana en lugar de la
media.
n
Desviación Media =
∑X
i =1
i
− med
n
M.A. Víctor Damián Pinilla Morán.
56
Es necesario comentar que debido a las
complejidades que implica el manejo del
valor absoluto, estos conceptos no son muy
socorridos.
Esto implica que debe cumplirse la
siguiente relación:
X < med < mod
Asimetría. Esta medida, también llamada
sesgo, tiene como finalidad mostrar hacia
qué lado de le media se ubican más datos.
Corresponde al tercer momento con
respecto a la media determinar esta
situación. No obstante, en situación similar
a lo que ocurre con la varianza, el tercer
momento posee las unidades de la variable
muestreada elevada al cubo.
α3 = 0
α3 > 0
Con el fin de volver adimensional al tercer
momento, se define al coeficiente de
asimetría de la siguiente forma:
α3 =
(
m3
m2
=
m3
) (σ )
3
3
2 2
α3 < 0
Este coeficiente tiene como referencia al
valor cero.
Si: α 3 = 0 La distribución es
simétrica, es decir, existe la misma
cantidad de datos a ambos lados de
la media.
Esto implica que debe cumplirse la
siguiente relación:
X = med = mod
Si: α 3 < 0 La distribución es
asimétrica negativa, es decir, existen
más datos a derecha de la media.
Esto implica que debe cumplirse la
siguiente relación:
mod > med > X
Si: α 3 > 0
La distribución es
asimétrica positiva, es decir, existen
más datos a izquierda de la media.
Probabilidad y Estadística
Noviembre 2009
Apuntamiento. Corresponde al cuarto
momento con respecto a la media
identificar a una medida que auxiliar
directamente a las medidas de dispersión.
El apuntamiento o curtosis detalla lo
puntiagudo o aplastado de una distribución.
Una distribución puntiaguda implica que
los datos están más cercanos a la media lo
que a su vez arroja una varianza pequeña.
En caso contrario, una distribución
aplastada implica que los datos se alejan de
la media, lo que implica una varianza
grande.
El cuarto momento con respecto a la media
posee las unidades de la variable
muestreada elevadas a la cuarta potencia.
Para mejorar una posible interpretación, se
define al coeficiente de apuntamiento o
coeficiente de curtosis:
α4 =
m4
(m2 )
2
=
m4
(σ )
2 2
M.A. Víctor Damián Pinilla Morán.
57
El valor de referencia de este coeficiente es
tres. Algunos autores, para homologar el
uso de este coeficiente con el de simetría,
disminuyen en tres unidades el valor
obtenido y así logran que el valor de
referencia sea cero.
α4 =
m4
m4
−3=
−3
2
(m2 )
(σ 2 )2
El lector deberá estar atento a esta
situación, ya que la gran mayoría de los
programas de computadoras realizan su
comparación contra el cero.
La interpretación es la siguiente:
Si α 4 = 0 (o tres), se trata de una
distribución mesocúrtica.
Si α 4 > 0 (o tres), se trata de una
distribución
Leptocúrtica
(o
puntiaguda).
Si α 4 < 0 (o tres), se trata de una
distribución
Platicúrtica
(o
aplastada).
_____________________________
Funciones de densidad de probabilidad
típicas de distribuciones: a) leptocúrticas, b)
platicúrticas, y c) mesocúrticas.
Bibliografía
Canavos, Probabilidad y Estadística,
Edit. Mc Graw Hill, México 1988.
Borras, et. al. Apuntes de Probabilidad
y Estadística, Facultad de Ingeniería
UNAM, México 1985.
Villarreal , Probabilidad y Modelos
Probabilísticos, UAEM, México 1989.
Hines, Montgomery; Probabilidad y
Estadística, Edit. CECSA, 3ª edición,
México 1993.
Captura y Edición:
M.A. María Torres Hernández.
Probabilidad y Estadística
Noviembre 2009
M.A. Víctor Damián Pinilla Morán.
58