problemas resueltos de estadística descriptiva

PR OBLE MAS R E SUE LTOS DE E STADÍ STI CAS DE SCRIPTI VA
Prof.: MSc. Ju lio R. Varg as
I.
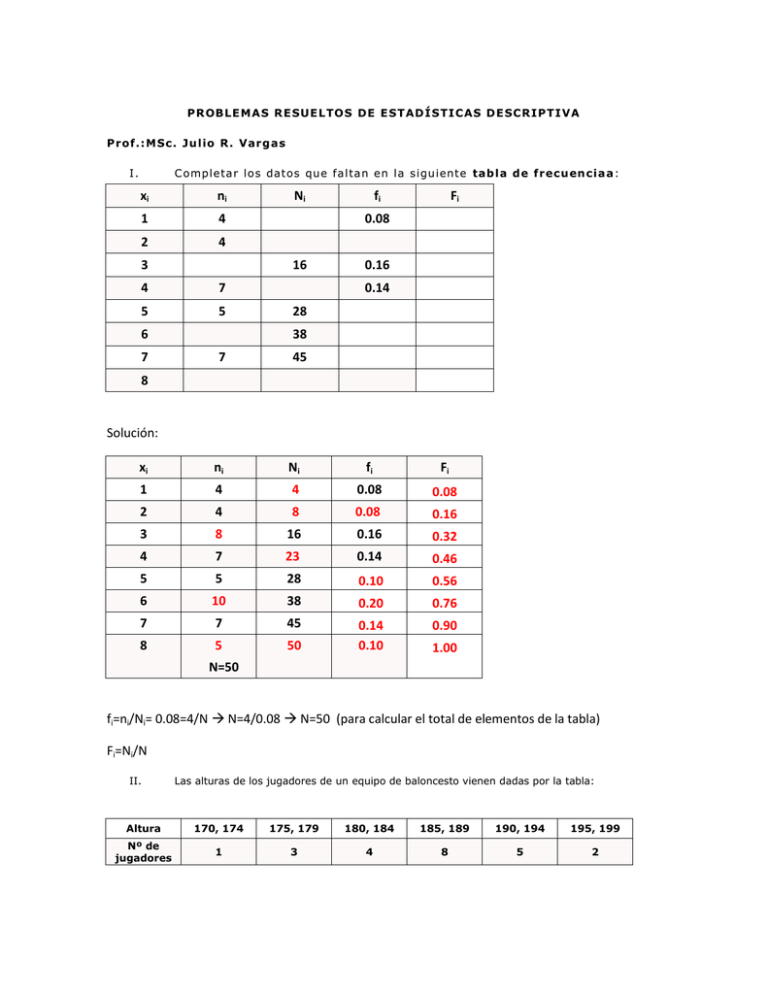
C ompleta r los da tos que fa lta n en la siguiente tab la d e frecu en cia a:
xi
ni
1
4
2
4
3
7
5
5
6
fi
Fi
0.08
16
4
7
Ni
0.16
0.14
28
38
7
45
8
Solución:
xi
ni
Ni
fi
Fi
1
4
4
0.08
0.08
2
4
8
0.08
0.16
3
8
16
0.16
0.32
4
7
23
0.14
0.46
5
5
28
0.10
0.56
6
10
38
0.20
0.76
7
7
45
0.90
8
5
50
0.14
0.10
1.00
N=50
fi=ni/Ni= 0.08=4/N  N=4/0.08  N=50 (para calcular el total de elementos de la tabla)
Fi=Ni/N
II.
Las alturas de los jugadores de un equipo de baloncesto vienen dadas por la tabla:
Altura
170, 174
175, 179
180, 184
185, 189
190, 194
195, 199
Nº de
jugadores
1
3
4
8
5
2
Calcular media y mediana.
Solución:
Intervalo
Xi
172
177
182
187
192
197
170, 174
175, 179
180, 184
185, 189
190, 194
195, 199
ni
1
3
4
8
5
2
∑
̅
Ni
1
4
8
16
21
23
Xini
172
531
728
1496
960
394
(media aritmética para datos agrupados)
Datos para el cálculo de la mediana en datos grupados.
Li=185
fa=8
fm=8
c=5
n/2=11.5
(
III.
)
(
)
L os resultados a l la nza r un da do 200 veces vienen da dos por la
siguiente tabla:
Xi
1
2
3
4
5
6
ni
a
32
35
33
b
35
D etermina r a y b sabiendo que la puntua ción media es 3.6.
Solución:
Como los resultados totales deben ser 200. La suma de:
a + 32 + 35 + 33+ b + 35 = 200
a + 135 + b= 200 esto es : a + b = 200-135  a+ b = 65
También nos dicen la media es 3.6
O sea
Xi
1
2
3
4
5
6
ni
a
32
35
33
b
35
Xini
a
64
105
132
5b
210
̅
∑
a + 5b = 200*3.6 – 511
a +5 b = 209
Ahora resolvemos el sistema de ecuaciones lineales:
{
Multiplicamos por -5 la primer ecuación y resulta
-5a +5b = -325
a + 5b = 209
--------------------4a = -116  a= 116/4  a= 29 entonces b= 65 -29=36
Por lo tanto sustituimos los valores en la primera tabla y quedará así:
Xi
1
2
3
4
5
6
ni
29
32
35
33
36
35
IV.
El histogra ma de la distribución correspondiente a l peso de 100 a lumnos de
Ba chillerato es el siguiente:
1.
F orma r la tab la d e la distrib uc ión .
2.
S i Jua n pesa 72 kg, ¿ cuá ntos a lumnos ha y menos pesa dos que él?
3.
Ca lcula r la mod a.
4.
Ha llar la med ian a .
S olución:
El histogra ma fue construido c on los límites inferiores y superiores de las
clases
y la a ltura de la s ba rra s del histograma son la s frecuencias de ca da
clase.
1) C onstruimos la ta bla de frecuencia
C la se
Xi
ni
Ni
fi
Fi
60 – 63
61. 5
5
5
0.05
0.05
63 – 66
64. 5
18
23
0.18
0.23
66 – 69
67. 5
42
65
0.42
0.65
69 – 72
70. 5
27
92
0.27
0.92
72 – 75
73. 5
8
100
0.08
1.00
2) Responderemos la pregunta 2: Jua n está en el último interva lo, por lo que
92 a lumnos tienen pesos menores que él.
3) Ca lculo de la M oda :
El límite inferior está en la clase que tenga la frecuencia a bsoluta más a lta .
L i = 66
∆ 1 = 42 – 18=24
∆ 2 =42 – 27=15
C= 3
(
)
(
)
4) Ca lculo de la mediana
El límite inferior es tá en la cla se que tenga la frecuencia absoluta a cumulada
que contenga a l 50% de los datos.
L i = 66
f a = 23
f m = 42
c= 3
(
V.
)
(
)
Los beneficios en millones de dólares de un grupo de empresas vienen detallados en el
siguiente histograma de frecuencias absolutas acumuladas:
En cientos de empresas
3
2.8
2.6
2.4
2.2
2
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
25
50
75
100
125
150
En millones de dólares
Calcular:
1. Tabla estadística
2. Establecer nº de empresas con beneficios superiores a 75 millones
3. Calcular media mediana y moda
S olución:
1.
T abla de frecuencia s o ta bla esta dística
B eneficios
No empresas
A cumuladas
Rela tivas
Rela tivas Ac
Xi
ni
Ni
fi
Fi
X in i
25
20
20
0.071
0.071
500
50
20
40
0.071
0.142
1000
75
80
120
0.286
0.428
6000
100
40
160
0.143
0.571
4000
125
60
220
0.214
0.785
7500
150
60
280
0.214
0.999꞊1
9000
2.
Número de empresas con beneficios superior a 75 millones: 160 emp resas.
3. Calcular media mediana y moda
3.1 Media aritmética:
∑
̅
3. 2
M edia na .
P rimero ca lculamos los límites inferior y superior de la ta bla .
Sa bemos que: X i = (L i + L s)/2
fórmu la de la ma rca de cla se.
a.
25 = (L i 1 + Ls 1 )/2 primera cla se
b.
C omo el ancho de la clase es ta mbién 25; lo cua l puede comproba r restando la
ma rca de cla se del segundo interva lo menos la del primero.
c.
C omo la ma rca de la cla se es el punto medio divi dimos el a ncho entre dos, eso
es 12. 5 solo toma remos la pa rte entera 12. L uego L i=25 -12=13
d.
El
L i de la segunda clase será : el lím ite inferior de la primera + 25 (a ncho de
la clase), ENTONCES L i 2 =13+25=38 y luego los otros
e.
P ara los límites superiores solo restamos 1(uno) a l limite inferior de la segunda
clase y será el límite superior de la primer clase. A sí obtenemos el resto.
La tabla de muestra a continuación.
Li
Ls
Xi
ni
13
37
Ni
25
20
20
38
62
50
20
40
63
87
75
80
120
88
112
100
40
160
113
137
125
60
220
138
162
150
60
280
El va lor de la mediana esta donde se encuentra el 50% de los da tos , en este caso la
frecuencia a cumula da que contenga a 140. Esta cla se la hemos ma rcado con amarillo.
L i = 88
f a = 120
f m = 40
c= 25
(
3. 3
)
(
)
millones
Ca lcula r la moda :
El límite inferior está en la cla se que tenga la frecuencia a bsoluta más a lta: en
este ca so es 80 , la cla se la hemos ma rcado con c olor na ranja.
L i = 63
∆ 1 = 80 – 20= 60
∆ 2 =80 – 40 = 40
C = 25
(
)
(
)