Puntos Muestral, Espacios Muestral y Diagrama de Árbol

Puntos Muestral, Espacios Muestral y
Diagrama de Árbol
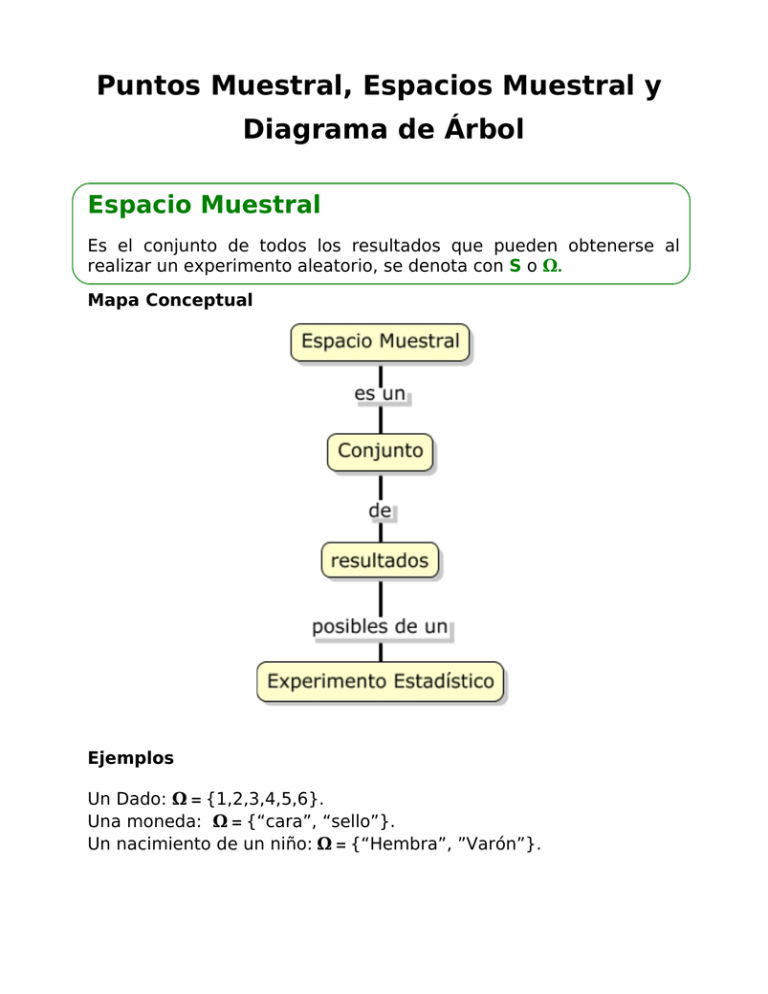
Espacio Muestral
Es el conjunto de todos los resultados que pueden obtenerse al
realizar un experimento aleatorio, se denota con S o Ω.
Mapa Conceptual
Ejemplos
Un Dado: Ω = {1,2,3,4,5,6}.
Una moneda: Ω = {“cara”, “sello”}.
Un nacimiento de un niño: Ω = {“Hembra”, ”Varón”}.
La mejor manera de escribir espacios muestrales con un número
grande o infinito de puntos muestrales es a través de planteamiento
o regla.
Por ejemplo:
S ={x|x es una ciudad de más de un millón de habitantes}.
que se lee “S es el conjunto de todas las x tales que x es una ciudad
con más de un millón de habitantes”. La raya vertical se lee “tal
que”. De manera similar, si S es el conjunto de todos los puntos (x,y)
que se encuentran en el límite o en el interior de un círculo de radio
igual a 2 y centro en el origen, se expresa:}
S ={(x,y)|x2 + y2
4 }.
El que se describa el espacio muestral a través de una regla o
listando sus elementos dependerá del problema específico que se
esté manejando. Establecer una regla tiene ventajas prácticas, sobre
todo en los muy abundantes experimentos en los que un listado se
convierte en una tarea bastante tediosa.
Punto Muestral
Es cada uno de los resultados de un espacio muestral.
En los ejemplos anteriores podemos decir que:
En un Dado, 1 ó 2 ó 3 ó 4 ó 5 ó 6 es cada uno de los puntos
muestrales al lanzar un dado.
En una moneda, “cara” ó “sello” es cada uno de los puntos
muestrales al lanzar una moneda.
En el nacimiento de un niño, “Hembra” ó “Varón” es cada uno de
los puntos muestrales en el nacimiento de un niño.
Casos Equiprobables
Es cuando los puntos muestrales de un experimento aleatorio tienen
todos la misma oportunidad de ocurrir, como es el caso del
lanzamiento de un dado, o de una moneda.
Diagrama de Árbol
Consiste en listar todos los elementos del Espacio Muestral en un
diagrama hecho de forma sistemática.
Éste ayuda a organizar cálculos que llevan varias etapas. Cada
segmento del árbol es una etapa del problema.
Mapa Conceptual