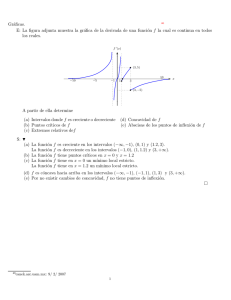
Cálculo de extremos. Resumen y ejemplos.

Cálculo de extremos. Resumen y ejemplos.
◦
Sea f : D → R, D ⊂ Rn , f ∈ C 2 . Buscamos sus extremos en D interior del dominio.
1) Condición necesaria. Al ser el conjunto abierto y f diferenciable, sus extremos
están en puntos que cumplan la condición de gradiente nulo. Entonces los posibles
extremos (puntos crı́ticos) son las soluciones de la ecuación
~ = ~0
∇f
2) Condición suficiente. Para determinar qué puntos crı́ticos son extremos, seguimos los pasos siguientes.
a) H definida. Aplicando el criterio de Sylvester, se averigua si H es definida.
Si es definida positiva, existe un mı́nimo. Si es definida negativa, un máximo.
b) Si H no es definida, estudiando su determinante tenemos dos casos:
6 0 . En este caso |D| = d1 d2 · · · 6= 0, pues |H| = |C|2 |D|, lo que significa
b.1. |H| =
que ningún di es nulo y pueden ser del mismo o distinto signo. Si tuvieran
igual signo, H serı́a definida, cosa que no ocurre. Entonces han de existir
di ≷ 0, por lo que H es indefinida y tenemos un punto de silla.
b.2. |H| = 0 . Entonces |D| = d1 d2 · · · = 0 luego los di pueden ser ≥ 0, ≤ 0 ó Q 0
(alguno es nulo), por lo que H puede ser semidefinida o indefinida.
En estos casos se puede conocer el tipo diagonalizando por congruencia. En
el caso particular n = 2, sólo existen dos di , de los que al menos uno es nulo.
No puede entonces ser indefinida, por lo que será semidefinida.
c) Casos dudosos (H semidefinida): para solucionarlos podemos probar distintas
direcciones de alejamiento desde el punto ~a. Si en una dirección la función crece
pero en otra decrece, se trata de un punto de silla. Lo mismo ocurre si, en la
misma dirección, crece en un sentido y decrece en el otro. En el caso n = 2, podemos
movernos desde ~a paralelamente a los ejes, o a las bisectrices y = x, y = −x.
3) Ejemplos.
a) f (x, y) = x2 + y 2 + xy − x − 2y.
Aplicando la
condición
necesaria, resulta el punto crı́tico P(0,1). La matriz hessiana
2 1
es H(0,1) =
. Según el criterio de Sylvester, H es definida positiva, por lo
1 2
que se trata de un mı́nimo.
b) f (x, y) = xy + x − y − 1.
Aplicando la condición
resulta el punto crı́tico P(1,–1). La matriz hes necesaria,
0 1
siana es H(1,−1) =
. En este caso, H no es definida (Sylvester). Como
1 0
|H| =
6 0, resulta que H es indefinida, por lo que tenemos un punto de silla.
c) f (x, y) =
√
R 2 − x2 .
Aplicando la C.N. =⇒
P(0,y) (son crı́ticos todos los puntos del eje Y ). En todos
1
−R 0
=⇒ |H| = 0 =⇒ H semidefinida (n = 2) =⇒ caso dudoso.
ellos, H =
0 0
1 dx2 ≤ 0, que
Para solucionarlo consideramos la diferencial segunda d2 f = − R
toma valor negativo ∀ dx 6= 0. Luego el valor de f disminuye si nos movemos,
desde los puntos (0, y) en cualquier dirección, salvo la dada por dx = 0. Pero
dx = 0 corresponde al eje Y , donde el valor de la función es constante. Es decir,
en todo punto (0, y) existe un máximo en sentido amplio.
Lo anterior se ve más claro haciendo z 2 +x2 = R2 , que es la ecuación de un cilindro
de radio R y eje
√ horizontal. Este eje no es otro que la recta x = 0 (eje Y ). La
expresión z = R2 − x2 corresponde a la parte superior del cilindro.
d) f (x, y) = y 3 − x2 − 2x − 1.
Aplicando la C.N. =⇒ P(−1, 0). H(−1,0)
−2 0
=
. La matriz H, diagonal, es
0 0
semidefinida negativa (caso dudoso).
Para resolverlo podemos –como en c)–observar que d2 f = −2dx2 . Esto nos indica
que el valor de f disminuye al movernos en cualquier dirección, salvo la del eje Y .
Estudiando este caso (variación sólo de la y), comprobamos que f crece si ∆y > 0
y decrece si ∆y < 0, por lo que es punto de silla.
Otra opción es movernos en las direcciones de los ejes, a partir de P(−1, 0), donde
f es nula. Ası́ pues, incrementamos alternativamente x e y en un valor ∆:
d.1. En cualquier punto de coordenadas (−1+∆, 0), la función toma el valor −∆2 ,
luego decrece, a partir de su valor en P, independientemente del signo de ∆.
d.2. En cualquier punto de coordenadas (−1, ∆), la función vale ∆3 . Es decir,
crece si nos movemos –a partir de P– en el sentido positivo del eje Y (∆ > 0),
y decrece en caso contrario.
Concluimos que, en P(−1, 0), f no tiene máximo ni mı́nimo (punto de silla).
e) f (x, y, z) = 3x2 − 6x + y 4 − z 4 .

Aplicando la C.N. =⇒ P(1,0,0). H(1,0,0)

6 0 0
=  0 0 0 .
0 0 0
H es semidefinida positiva (caso dudoso) y la diferencial segunda vale d2 f = 6dx2 ,
por lo que la función crecerá siempre que dx 6= 0. Si, en cambio nos movemos
a partir de P , paralelamente al plano Y Z, d2 f = 0. Para identificar el tipo de
extremo, nos movemos a partir de P, modificando el valor de las variables y y z,
una cada vez:
e.1. Valor de f en P: f (1, 0, 0) = −3
e.2. Incrementamos y: f (1, ∆, 0) = −3 + ∆4 =⇒ ∆f = ∆4 , luego f crece.
e.3. Incrementamos z: f (1, 0, ∆) = −3 − ∆4 =⇒ ∆f = −∆4 , luego f decrece.
Se trata, entonces, de un punto de silla. No hemos probado a modificar el valor de
la x, pues d2 f = 6dx2 : esto nos indica que al variar x, d2 f será mayor que 0, por
lo que la función crecerá (compruébese).