Fisica II: Campo E a una distancia r de una línea de carga infinita

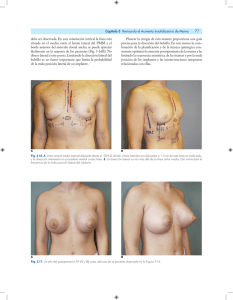
LÍNEA INFINITA DE CARGA
Fig. 14
La figura 14 muestra una sección de una línea infinita de carga de densidad constante.
Deseamos calcular el campo eléctrico a una distancia R de la línea.
Solución: Si suponemos la carga del alambre positiva, el sentido del campo será
radialmente hacia fuera, y su magnitud dependerá de la distancia radial R . Como
superficie gaussiana elegimos un cilindro circular de radio R y longitud h. Al utilizar la
Ley de Gauss,
εo ∫ E ⋅ds = q
se descompone la integral en tres integrales, dos con respecto a las bases del cilindro y
una con respecto a la superficie lateral. Como no hay flujo a través de las bases sino
solamente a través del área lateral, y como por simetría E tiene el mismo valor en todos
los puntos de esta última, se tendrá que
r r
q = ε o ∫ E ⋅ ds
= ε o ∫ Eds cos 0°
= ε o E ∫ ds
= ε o Es
= ε o E (2πRh) = λh
Pues el área lateral del cilindro es 2πRh y la carga total encerrada es la densidad lineal
de carga multiplicada por la longitud, y resulta
E=
1
λ
2πε o R
En la unidad sobre Interacción Eléctrica (Problema resuelto #8, alambre infinito) se
obtuvo este mismo resultado utilizando una técnica de integración a partir de la
expresión
E = K∫
dq
ûr
r2
la cual utilizaba un método más laborioso. El resultado obtenido también es válido para
alambres cargados con longitud finita, siempre que la distancia radial, R , sea mucho
menor que la distancia L a un extremo del mismo, es decir
R << L
Fig. 15