Ejercicios-de-Prismas-y-Cilindros-Para-Segundo-Grado-de-Secundaria

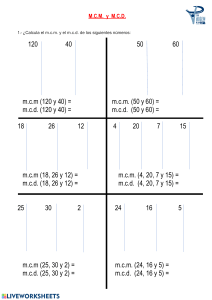
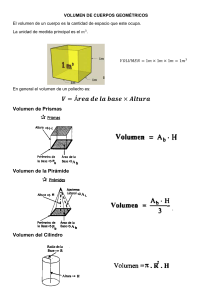
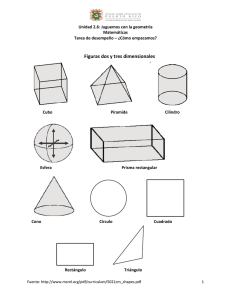
EJERCICIOS DE PRISMAS Y CILINDROS
I. PRISMA
Es aquel sólido geométrico que se encuentra limitado superior e inferiormente por dos regiones
poligonales paralelas y lateralmente, se encuentra
limitado por regiones paralelográmicas.
B
C
A Base
D Arista
basica
Arista
Lateral
F
G
Base
Vértice
E
H
Clasificación
1. Prisma recto
Es aquel que tiene sus aristas laterales perpendiculares a las bases. Sus caras laterales
son rectangulares.
2. Prisma oblicuo
Es aquel prisma cuyas aristas laterales son
oblicuas a las bases. Sus caras laterales son
paralelogramos.
(I)
(II)
II. CILINDRO
Es el sólido obtenido al interceptar una superficie
cilíndrica cerrada, por medio de dos planos paralelos.
Las regiones que determinan dichos planos son
las bases del cilindro y la distancia entre ellos es la
altura.
h
cilindro recto cilindro oblicuo
Si los planos son perpendiculares a las generatrices, el cilindro es recto; en caso contrario, es oblicuo. En ambos casos las bases son congruentes.
Cilindro de revolución
Se genera al girar (360°) una región rectangular
alrededor de un eje que contiene a un lado. Las
bases son círculos y la altura mide igual que la
generatriz. Es también llamado, cilindro circular.
x
h
R
g
g
Sus bases son regiones triangulares, cuadrangulares, pentagonales, etc.
3. Prisma regular
Es un prisma recto, cuyas bases son polígonos
regulares.
ASL: área de la superficie lateral
AST: área de la superficie total
V: volumen
ASL = Arista x Perímetro
de la base
lateral
AST = Área + 2 Área
base
lateral
V = Área x Altura
base
R
R
R
y
R: Radio
g: generatriz
h h: altura
y
Área de la superficie lateral de un cilindro (ASL).
El área lateral de un cilindro circular recto es igual
al producto de la longitud de la circunferencia de
su base por su altura.
ASL = 2pR • g
Área de la superficie total de un cilindro (AST)
AST = ASL + 2(Ab)
Ab: área de la base
Volumen de un cilindro (VCil)
Nota:
VCil = Ab x h
Además de las clases de primas que
hemos visto también tenemos: el prisma
irregular, el paralelepípedo, el ortoedro, el
prisma triangular y el cuadrangular.
VCil = pR2 x h
Trabajando en clase
Integral
1. Calcula el volumen del rectoedro.
F
G
H
B
E
1m
A
C
1m
4m
D
2. Determina el volumen del paralelepípedo.
F
E
3m
G
H
B
37°
C
3m
A
D
3. Calcula el volumen del rectoedro.
F
E
1m
A
45°
G
H
B
1m D
C
1m
E
Resolución:
Según la figura:
I
C
F
G
2m
2m
A 1m D
H
B
1m M
E
I
F a
C
luego volumen = 1 m x a x 2 m = 6 m3.
5. Indica el volumen del paralelepípedo.
F
B
E
2m
A
G
2mH
C
4m
3m
D
6. Calcula el área total del rectoedro.
F
B
E
A
1m
G
H
2m D
C
3m
7. Encuentra el volumen del cilindro.
C
10 m
4. Calcula el volumen del rectoedro.
B
1m
2
B
Católica
H
ABCD es un trapecio y MN es base media
a+1
→2m=
→ a= 3m
G
N
2m
2m
A 1m D
o
A
4u
D
UNMSM
8. La figura muestra un tarro de leche cuya altura es
12 m y radio de la base 4 m. Calcula el área de la
etiqueta.
B
C
12 m
A
o
4m
D
11. En la figura se muestra un cilindro, calcula su
área lateral. «O» es centro.
B
C
Resolución:
Según la figura:
B
C
12 m
A
12 m
o
4m
etiqueta
D
2p x 4m
Luego:
Área de la
2
etiqueta = base x Altura = 8pm x 12 m = 96p m .
9. La figura muestra un tarro de leche cuya altura es
16 m y radio de la base 3 m. calcula el área de la
etiqueta.
B
C
16 m
o
A
3m
D
10. Calcula la cantidad de agua que puede almacenar
el cilindro del gráfico si tiene 2 m de diámetro de
la base y 6 m de altura.
B
A
C
o
D
3u
A
37°
D
o
UNI
12. En un cilindro recto su generatriz mide 7 u, el
área de su base es 4p u2, calcula su área lateral,
área total y volumen
B
C
Resolución:
Según los datos:
7m
Área de la base
r
D
o
A
del cilindro = pr2 = 4p u2
→r=2u
luego: área lateral = 2pr.h = 2p.2u.7u = 28p u2
área total = 2p r(h + r) = 2p.2u(7u + 2u)
= 36 p u2
Volumen = pr2h = p(2u)2.7u = 28p u2
13. En un cilindro recto su generatriz mide 10 u, el
área de su base es 9p, calcular su área lateral, área
total y volumen.
14. Calcula el volumen y área total de un cubo en el
cual la suma de las longitudes de todas las aristas
es 36 m.