El Movimiento de los Planetas

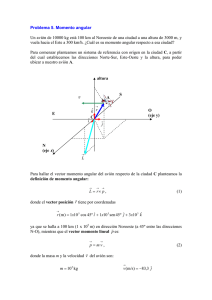
El Movimiento de los Planetas
> INTRODUCCIÓN
La Tierra, junto con todos los planetas de nuestro sistema planetario el Sistema
Solar, realizan dos movimientos fundamentales, el movimiento de translación y el
movimiento de rotación. Para entender la explicación física de los movimientos
anteriores, antes tenemos que explicar brevemente el momento lineal y el momento
angular:
A) MOMENTO LINEAL
El momento lineal (p), es una magnitud vectorial, que se define como el
producto de la masa y la velocidad en un instante determinado.
p=m·v
•
•
•
p = Momento Lineal (kg · m/s)
m = Masa (Kg)
v = Velocidad (m/s)
El momento lineal se conserva cuando un sistema de partículas no recibe
impulso del exterior.
B) MOMENTO ANGULAR
El momento angular (L), es otra magnitud vectorial que se define como el
producto vectorial del vector de posición por el momento lineal.
L = r x p = m (r x v)
•
•
•
•
•
L = Momento Angular (kg · m2/s)
p = Momento Lineal (kg · m/s)
m = Masa (Kg)
v = Velocidad (m/s)
r = Medida del "Brazo" (m)
El momento angular se conserva si sobre la partícula sólo actúan fuerzas
centrales.
La Interacción Físico-Gravitatoria >> Bloque 2 >> Tema 13
2006 - Diego Cabaleiro
1
El Movimiento de los Planetas
> MOVIMIENTO DE TRANSLACIÓN
A) INTRODUCCIÓN AL MOVIMIENTO
Todos los planetas del sistema solar giran alrededor del sol, este movimiento es
conocido como movimiento de translación. En el caso de la Tierra, el giro
completo dura aproximadamente 365 días y 6 horas.
Fig1-T13: Movimiento de translación de tres planetas del Sistema Solar
B) ESTUDIO FÍSICO DEL MOVIMIENTO
Para estudiar el movimiento de translación tenemos que buscar una magnitud
que describa el movimiento y permanezca constante. No podemos utilizar el
momento lineal o cantidad de movimiento, ya que no permanece constante:
Fig2-T13: Representación del vector momento lineal en diferentes puntos del
movimiento de translación de un planeta.
Comos vemos en la figura anterior, la dirección del vector momento lineal, no
permanece constante, por lo que no se conserva el momento lineal. (NOTA: El
módulo del vector momento lineal también puede cambiar)
Entonces tenemos que hacer uso del momento angular, que sí se conserva. El
campo gravitatorio es un campo de fuerzas centrales en el que r y F son paralelos,
con lo que concluimos que el momento de la fuerza es igual a 0, el momento
angular es conservativo.
La Interacción Físico-Gravitatoria >> Bloque 2 >> Tema 13
2006 - Diego Cabaleiro
2
El Movimiento de los Planetas
C) CONSECUENCIAS DE LA CONSTANCIA DEL MOMENTO ANGULAR
•
•
•
•
Las órbitas planetarias son planas
Las órbitas planetarias son estables
Las órbitas de los satélites de los planetas, también son planas y estables
La fuerza que gobierna los planetas y los satélites de estos, es de tipo central
Fig3-T13: Fuerza Central de un planeta en una órbita plana
> MOVIMIENTO DE ROTACIÓN
A) INTRODUCCIÓN AL MOVIMIENTO
Los planetas del Sistema Solar, aparte de girar alrededor del Sol, también giran
sobre si mismos, este movimiento es conocido como movimiento de rotación. En
el caso de la Tierra, el giro completo dura 24 horas y da lugar a la sucesión díanoche.
Fig4-T13: Movimiento de Rotación de un planeta
B) ESTUDIO FÍSICO DEL MOVIMIENTO
En la Tierra, gracias a la ausencia de momentos de fuerza netos actuando en
la Tierra, se conserva el momento angular, y por lo tanto el movimiento de
rotación.
La Interacción Físico-Gravitatoria >> Bloque 2 >> Tema 13
2006 - Diego Cabaleiro
3