Funciones_Crecientes_y_Decrecientes

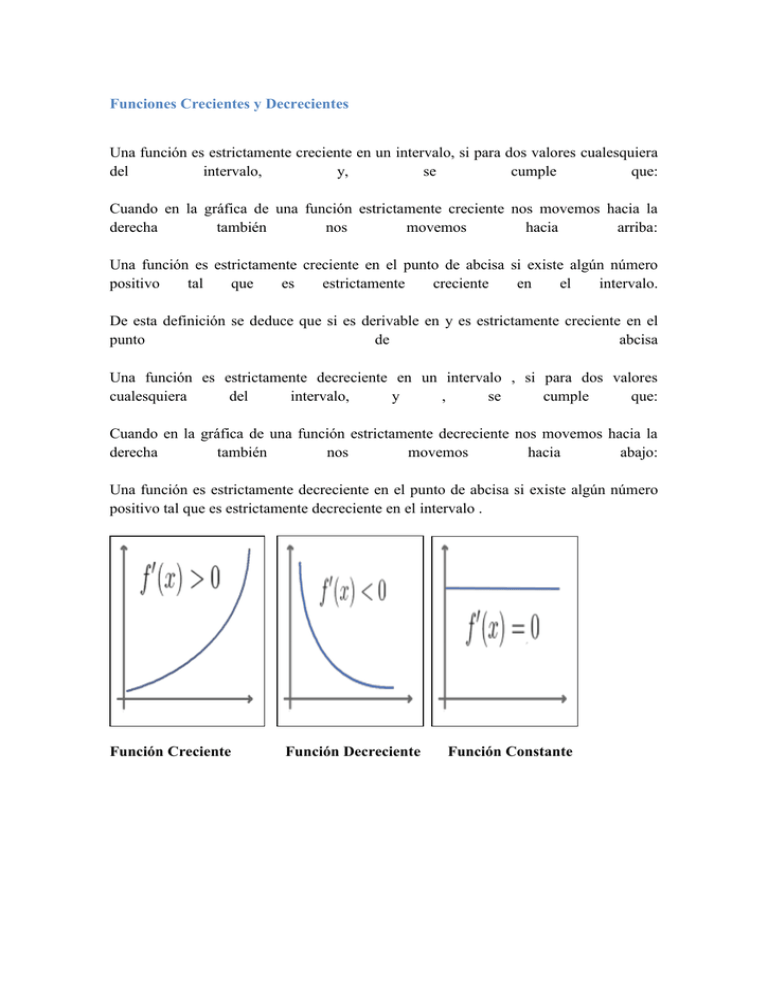
Funciones Crecientes y Decrecientes
Una función es estrictamente creciente en un intervalo, si para dos valores cualesquiera
del
intervalo,
y,
se
cumple
que:
Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la
derecha
también
nos
movemos
hacia
arriba:
Una función es estrictamente creciente en el punto de abcisa si existe algún número
positivo
tal
que
es
estrictamente
creciente
en
el
intervalo.
De esta definición se deduce que si es derivable en y es estrictamente creciente en el
punto
de
abcisa
Una función es estrictamente decreciente en un intervalo , si para dos valores
cualesquiera
del
intervalo,
y
,
se
cumple
que:
Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la
derecha
también
nos
movemos
hacia
abajo:
Una función es estrictamente decreciente en el punto de abcisa si existe algún número
positivo tal que es estrictamente decreciente en el intervalo .
Función Creciente
Función Decreciente
Función Constante
Funciones crecientes y decrecientes
Una función
es creciente es un intervalo si para cualquier par de números
intervalo.
Una función
.
es decreciente es un intervalo si para cualquier par de números
intervalo,
del
del
.
Sea f una función continua con ecuación
siguiente es la representación gráfica
, definida en un intervalo
. La
de f en el intervalo
.
En la gráfica anterior puede observarse que la función f es:
1.) Creciente en los intervalos
2.) Decreciente en los intervalos
Criterio de crecimiento y decrecimiento
Sea
una función continua en el intervalo cerrado
abierto
y derivable en el intervalo
.
1. Si
es creciente en
2. Si
es decreciente en
3. Si
es constante en
Ejemplo 1
Determinemos
ecuación
los
intervalos
en
que
o
decrece
la
función
.
Para ello calculemos la primera derivada de
Como
crece
↔
, o sea si
.
, entonces f es creciente para
.
con
Como
↔
, o sea si
, entonces f es decreciente para
.
En la gráfica de la función puede observarse lo obtenido anteriormente.
Ejemplo 2
Determinar
ecuación
los
La derivada de f es
Como
intervalos
en que crece
, con x ≠ 1.
o
decrece
la
función
f
con
.
es mayor que cero para x en los Reales, x ≠ 1, y además
entonces
para todo x en los Reales (x ≠ 1), por lo que la función f es decreciente para x
en los Reales, x ≠ 1 . La siguiente, es la gráfica de dicha función:
Ejemplo 3
Determine en cuáles intervalos crece o decrece la función con ecuación
con x ≠ 0.
La derivada de f está dada por
Como
que puede escribirse como
es positivo para toda x en los Reales entonces:
y
←→
</tex> ←→
Para resolver estas desigualdades recurrimos a la siguiente tabla.
Luego:
Además:
∞
si
∞.
si
€
∞ por lo que la función f crece en el intervalo
€
∞
de donde la función f decrece en el intervalo
.
La representación gráfica de la función es la siguiente:
Ejemplo 4
Trace la gráfica de la función definida por
Determine a partir de la gráfica los extremos relativos de , los valores de en los que
ocurren los extremos relativos, los intervalos en los que es creciente, y en los que
decrece. Confirme analíticamente la información obtenida gráficamente. Solución La
siguiente grafica muestra a
trazada en el rectángulo de inspección de
por
. A partir de esta gráfica, se determina que tiene un valor máximo
relativo de 5 en
, y un valor mínimo relativo de 1 en
. También, a partir de la
gráfica se determina que
es creciente en los intervalos
y
, y es
decreciente en v
el intervalo
.
Ahora se confirmará esta información mediante el criterio de la primera derivada
calculando primero la derivada de :
Los únicos números críticos son aquellos para los que
:
Por tanto, los números críticos de son 1 y 3. Para determinar si tiene un extremo
relativo en estos números, se aplica el criterio de la primera derivada y los resultados se
presentan en la tabla:
Las conclusiones de la tabla confirman la información determinada gráficamente.
Ejemplo 5
Sea
Determine los extremos relativos de y los valores de
en donde ellos ocurren.
También determine los intervalos en los que es creciente y en los que es decreciente.
A poye las respuestas gráficamente.
Solución Al diferenciar
se tiene
Como
no existe cuando
,y
cuando
, entonces los números
críticos de f son -1 y 0. Se aplica el criterio de la primera derivada y se resumen los
resultados en la siguiente tabla:
La información de la tabla se apoya a trazar la gráfica de
en el rectángulo de
inspección de
, como se muestra en la siguiente gráfica
Demostración
Creciente
Supongamos que
y sean
dos puntos arbitrarios del
intervalo. Por el teorema del valor medio, sabemos que existe algún c tal que
y
Como
y
, sabemos que
De donde se deduce que
. Así pues,
es creciente en el intervalo.