Estudio de procesos dinamicos por RMN

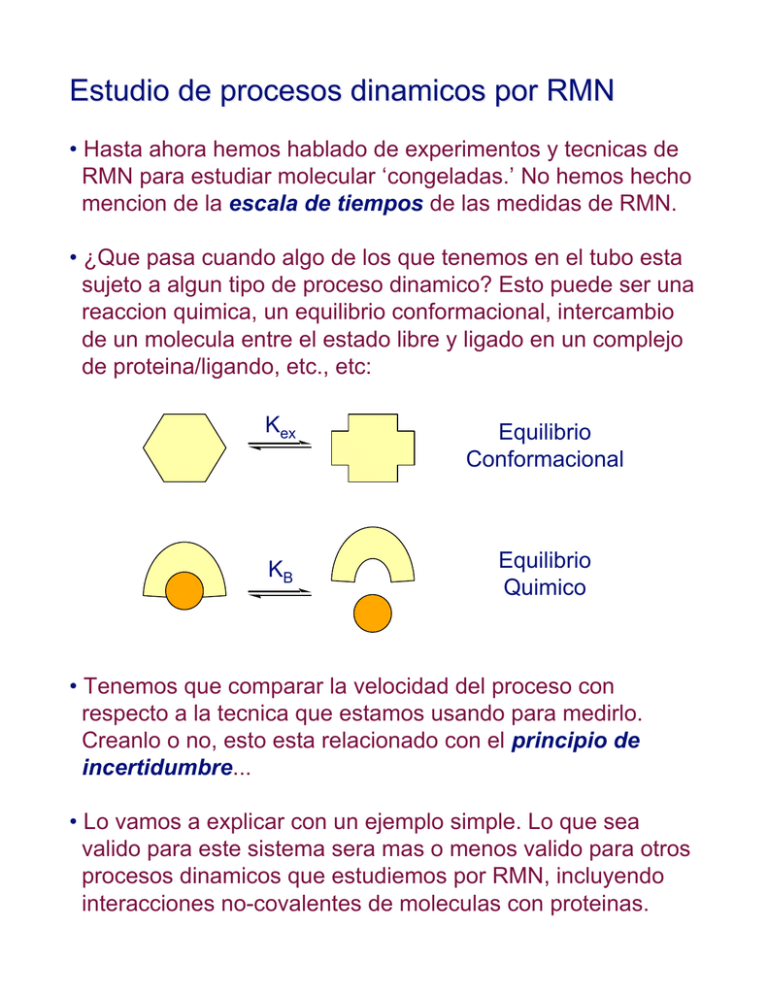
Estudio de procesos dinamicos por RMN
• Hasta ahora hemos hablado de experimentos y tecnicas de
RMN para estudiar molecular ‘congeladas.’ No hemos hecho
mencion de la escala de tiempos de las medidas de RMN.
• ¿Que pasa cuando algo de los que tenemos en el tubo esta
sujeto a algun tipo de proceso dinamico? Esto puede ser una
reaccion quimica, un equilibrio conformacional, intercambio
de un molecula entre el estado libre y ligado en un complejo
de proteina/ligando, etc., etc:
Kex
Equilibrio
Conformacional
KB
Equilibrio
Quimico
• Tenemos que comparar la velocidad del proceso con
respecto a la tecnica que estamos usando para medirlo.
Creanlo o no, esto esta relacionado con el principio de
incertidumbre...
• Lo vamos a explicar con un ejemplo simple. Lo que sea
valido para este sistema sera mas o menos valido para otros
procesos dinamicos que estudiemos por RMN, incluyendo
interacciones no-covalentes de moleculas con proteinas.
Medida de constantes de velocidad
• Digamos que el proceso que estamos analizando es la
inversion de la N,N-dimetilformamida (DMF):
O
N
O
H
N
H
• Sabemos que los metilos rojo y azul van a intercambiar
sitios relativamente lento debido al caracter de doble enlace
de la amida. Los dos metilos son quimica y magneticamente
diferentes, y un espectro RMN de la DMF da una señal para
cada metilo:
• Esto significa que el intercambio entre los dos sitios es lo
suficientemente lento comparado a la diferencia de frecuencia
relativa entre las resonancias de las dos especies (roja y
azul):
1
Intercambio (s) >>
1
o
δr - δa
Δδ
Constantes de velocidad (continuado)
• Ahora empezamos a calentar la muestra. Como la velocidad
de la inversion depende de su ΔG y este esta afectado por
T, temperaturas mas altas hacen que las cosas vayan mas
rapido. Vemos lo siguiente:
T
TC
• A cierta temepratura, llamada la temperatura de
coalesenscia, la constante de intercambio entre las
especies es comparable a la diferencia de corrimiento
quimico entre los dos sitios:
1
Intercambio (s) ~
1
o
δr - δa
Δδ
• Despues de este punto, no podemos distinguir un sitio de
otro con medidas de RMN porque el intercambio ocurre
mas rapido que la diferencia de frecuencia relativa.
Constantes de velocidad (mas...)
• Vemos que hay dos regiones a medida que variamos la
temperatura, llamdas de intercambio rapido y lento:
Δδ * velocidad > 1
Intercambio lento
Δδ * velocidad = 1
Transicion (TC)
Δδ * velocidad < 1
Intercambio rapido
• Como podemos estimar la temperatura de la transicion (la
temperatura de coalecenscia), podemos sacar datos acerca
de la termodinamica y la cinetica del proceso.
• Si hiciecemos un estudio detallado, veriamos que tenemos
que tomar en cuanta las poblaciones de los dos sitios (uno
puede estar mas favorecido que el otro energeticamente),
asi como tambien los anchos de linea de los picos.
• Como hicimos con otras derivaciones matematicas, vamos
a usar resultados aproximados que sirven para lo que
queremos explicar.
• Nos concentramos en el caso con sitios igualmente
populados (energias iguales), osea que la diferencia de
energia libre es debida solo al proceso de intercambio que
estemos estudiando.
Constantes de velocidad (...y mas)
• A partir de Δδ (en Hz) en el limite de intercambio lento
calculamos la constante de intercambio a la temperatura de
coalecenscia:
Kex = π * Δν / √ 2 = 2.22 * Δν
• Usamos frecuencias en radianes y por eso es que aparece
el factor de π. Esta ecuacion tiene muchas simplificaciones
(nunca sabremos si la temperatura mas baja a la que hicimos
el experimento es realmente intercambio lento, y no
consideramos los anchos de linea).
• De cualquier manera, funciona bastante bien. Con la
temperatura de coalecenscia calculamos el ΔG‡ del proceso
con otra relacion aproximada:
ΔG‡ = R * TC* [ 22.96 + ln ( TC / Δν ) ]
• Si no tomamos en cuenta las contribuciones entropicas al
ΔG‡, podemos calcular las constantes de reaccion a cualquier
otra temperatura solo con esta informacion.
• Con RMN podemos medir constantes entre 10-2 y 108 s-1.
Ejemplo de equilibrio conformacional
• Como parte de mi trabajo con taxol, trate de preparar una
analogo de la cadena lateral rigido para evaluar si el imponer
rigidez mejoraba o empeoraba la actividad biologica.
• Decidi hacer un sistema bifenilo, que a la larga demonstro
ser una muy mala idea. Si hubiese leido un poco hubiese
sabido que estas cosas se comportan medio raro....
• Considerado que tengo 10 pulgares, hacerlo fue todo un
logro (me llevo muuuuucho tiempo). Al tomar un 1H, vi que
al parecer tenia dos ‘cosas’ en solucion:
O
O
NH
O
NH
OMe
OMe
OH
O
OH
• Algo estaba mal. Tenia solo una manchita por TLC, asi que
las cuentas no me cerraban. Llegue a la conclusion de que
teniamos un equilibio lento de dos conformeros en
solucion, algo que los bifenilos hacen (haber leido...).
Equilibrio conformacional (continuado)
• Como me habia matado por 4 meses haciendo esto, no lo
iba a dejar por eso. Tambien, tener dos conformeros no era
bueno para probar nada. Si esto era un equilibrio, un cambio
en temperatura tenia que afectar las velocidades de
intercambio:
• Vimos que a) habia coalesencia de los dos grupos de
señales entre 80 y 100oC, y b) que el proceso era reversible.
Equilibrio conformacional (mas…)
• En este caso, la inversion de los anillos no ocurre sola, y
hay otros cambios conformacionales asociados. Tambien
puede haber puentes-H formandose/rompiendose, asi que
es dificil elegir dos señales para hacer los calculos de la
barrera de energia de inversion.
• Si elejimos un par de picos aromaticos (los anillos son los
se que invierten), medimos un δν de 0.04 ppm (o 20 Hz a
500 MHz):
20 Hz
• Considerando que la coalecensia de estos dos picos ocurre
a ~85oC (358 K), y usando la formula para ΔG‡:
Kex ~ 44.4 s-1
ΔG‡ ~ 18.5 Kcal/mol
• No esta tan mal despues de todo…
Conformacion de ligandos - TRNOE
• Una de las cosas mas importantes en el diseño de drogas
es averiguar como se ligan a su receptor, Que generalmente
es una proteina o ADN.
• Con esta informacion e informacion de las REA podemos
preparar analogos que no solo tengan los requerimientos
quimicos para ser activos, pero tambien los requerimientos
conformacionales impuestos por el sitio activo.
• Una forma es estudiar la conformacion de la molecula aislada
(por rayos-X o RMN), y asumir que va a tener la misma
cononformacion en el sitio activo.
• En moleculas flexibles (el 99.9% de los casos…), el cambio
en el entorno (polaridad, grupos no-polares, puentes-H, etc.)
al pasar del agua al sitio activo va a afectar la conformacion.
+
Libre
Ligado
• Osea, para estudiar la conformacion del ligando en el sitio
activo hay que estudiarlo en el sitio activo o bajo el ‘efecto’
del sitio activo…
Conformacion de ligandos (continuado)
• Dependiendo del tamaño del receptor podemos determinar
la estructura del complejo y usar eso (rayos-X, RMN).
• Esto consume muchisimo tiempo, y vamos a estar
determinando, principalmente, la estructura del receptor.
Lo que queremos es saber la conformacion del ligando...
• Ademas, la mayoria de los receptores son enormes (de 100
a 200 KDa), y los interesantes estan en membranas, osea
que no les podemos (¿podiamos?) entrar con nada.
• Lo que, en algunos casos, nos salva son las diferencias
relativas entre la velocidad de crecimiento del NOE para
protones del ligando (la velocidad de crecimiento de la
relajacion cruzada) y las constantes de asociacion entre el
ligando y el receptor.
• Digamos que tenemos el siguiente complejo ligando/receptor:
*
HI
*
HS
• Cuando este en el sitio activo
los protones indicados van a
tener NOE. Van a ser muy
dificiles de ver en el complejo
poque vamos a tener toneladas
de NOE’s del receptor consigo
mismo.
Conformacion de ligandos (mas…)
• Supongamos que el ligando se disocia y vuelve a la solucion
Va a adoptar su conformacion en solucion rapidisimo:
HI
*
HI
*
koff
*
H
HS kon
*
H
kunf
*
*
HS
• Generalmente, koff (o la constante de disociacion) es mucho
mas lenta que kunf (la velocidad a la que el ligando sufre
‘unfolding’), osea que solo nos preocupamos por koff.
Definimos todas las constantes de la siguiente forma:
K=
kon
koff
[ligando-receptor]
=
[receptor] [ ligando]
• Independientemente de la constante koff, la interaccion NOE
entre los dos protones que aparecio cuando el ligando estaba
en el sitio activo va a persistir por un tiempo (que depende de
la relajacion espin-red, T1).
Conformacion de ligandos (y mas…)
• Esto significa que si el proceso de asociacion/disociacion es
rapido comparado con T1, el NOE que surgio entre los 1H’s
cuando el ligando estaba en el sitio activo va a persistir luego
de que el ligando se disocie y adopte su conformacion en
solucion ¿Porque?
• Tenemos que considerar todo el proceso:
RIF
IF
Kon
koff
σISF
RSF
IB RIB
σISB
SF
Kon
koff
SB
RSB
• El acople diploar entre I y S ocurre para el ligando en el sitio
activo (‘bound,’ IB, SB) y en solucion (‘free,’ IF, SF). Cuando
el ligando este en el sitio activo, su tiempo de correlacion va
a ser enorme (tenemos a la proteina), y la relajacion cruzada
entre I y S esta dominada por σISB.
• Por eso los NOE’s que surgen en el sitio activo persisten en
solucion. Ademas, en el complejo el ligando va a tener un
ω * tc aprente mayor que 1, y siempre vamos a estar sobre
el limite de difusion de espin (osea, NOE’s negativos...).
Conformacion de ligandos (y mas...)
• Es mas, si tenemos buen intercambio (‘turnover’)
comparado con el tiempo de relajacion T1, vamos a tener
varios ligandos interactuando con el mismo receptor antes de
que el NOE del primero decaiga.
• Osea, podemos hacer el experimento con un exceso de
ligando (i.e., 10 veces mas), y las señales del ligando van a
ser mas grandes que las del receptor (que van a ser anchas
y van a aparecer todas superpuestas...).
• Otra cosa buena de medir NOE’s de ligandos en el sitio
activo por TRNOE es que como vamos a estar mirando al
ligando en solucion, sus señales van a estar bien definidas
(anchos de linea relativamente chicos) :
L ligado
L libre
proteina
• Las señales ‘finas’ son mas altas (tienen la misma area), se
diferencian bien del ‘background’ de la proteina, y dan
cross-peaks mucho mejor resueltos en un experimento 2D.
Conformacion de ligandos (…y mas)
• Si parece demasiado bueno para ser verdad, es demasiado
bueno para ser verdad. Para poder usar TRNOE se tienen
que dar un monton de cosas (todas juntas):
• El ligando no puede interactuar mucho con el receptor,
ya que necesitamos intercambio constante entre los
ligandos libres y los ligandos en el sitio activo.
• La constante Koff tiene que ser mucho mas chica que
el tiempo de relajacion T1, sino el NOE desaparece
antes de que lo podamos detectar.
• En la practica, esto limita mucho el tipo de sistemas que
podemos analizar usando esta tecnica...
Gradientes de campo magnetico y difusion
• Todo lo que hemos visto sucede en campos magneticos
‘perfectos’ (i.e., Bo homogeneos). Esto lo necesitamos para
tener buena resolucion/sensibilidad. Sin embargo, crear un
gradiente con caracteristicas conocidas en Bo es muy util.
• Un gradiente de campo resulta en diferentes Bs. Si solo
consideramos una variacion linear en el eje z (i.e., un
gradiente-z, o Gz) y una muestra de agua, veremos que las
moleculas de agua con distintas zs tendran diferentes δs
(porque δ ∝ γ (Bo+ Gz)):
Bo
δ
Bo+ Gz
δ
• La señal es proporcional a la ‘masa’ en la muestra…
Gradientes de campo magnetico (continuado)
• Y esto es util? Para empezar, podemos generar una imagen
de la muestra si aplicamos un gradiente durante la
adquisicion de datos. Como los espines en distintos lugares
del tubo tienen distintos δs, obtenemos un espectro ‘continuo’
que refleja la forma del contenedor.
ω (Hz)
Bo+ Gz
• Osea, un gradiente de campo linear deja a los espines
codificados espacialmente. Esto significa que ‘sabemos’ a
que parte del tubo (o ‘brazo’) pertenecia el espin basados en
el gradiente que aplicamos. Si agregamos contraste basado
en los tiempos de relajacion del agua en distintos tejidos
obtenemos RMI (mas o menos…).
• Ademas, si combinamos gradientes de distinto signo
podemos codificar los espines, dejarlos evolucionar (pulsos,
tiempos, etc.), y luego decodificarlos.
• Espines que (no) se comportan de cierta manera durante el
periodo de evolucion, (no) aparecen en el espectro…
Gradientes y difusion
• Y esto deriva en medidas de difusion. Medir el coeficiente
de difusion (D) es muy importante en quimica/biologia.
Reporta sobre mobilidad de moleculas, interacciones
intramoleculares, etc., etc.
• La espectroscopia de gradientes de campo pulsados es ideal
para medir la difusion de particulas con nucleos que poseen
RMN. La tecnica mas basica implica combinar un eco de
espin con dos gradientes de signo opuesto y largo δ
separados un tiempo Δ:
90y
180y
Δ/2
1H:
Δ/2
Δ
Canal de
gradientes:
δ
δ
• Hay que analizar que hara el eco de espin bajo los efectos
del gradiente codificador/decodificador sobre nucleos que
difunden a distintas velocidades. Hay que recordar que un
gradiente hace que las cosas se muevan mas rapido/lento en
el sistema rotatorio (i.e., cambian el ‘corrimiento quimico’).
Gradientes y difusion (continuado)
• Para un espin que se mueve poco (luego del pulso π / 2):
y
y
G(δ)
x
x
y
180
Δ/2
y
-G(δ)
x
Δ/2
x
• Aca los puntos rojo/azul representan al mismo tipo de nucleo
en distintas regiones del ‘tubo’…
• Basicamente, como el espin no se mueve los gradientes
tienen poco efecto. Osea, el espin no se movio del area
original, y el gradiente decodificador tiene un efecto igual y
opuesto al codificador (reenfoque). En otras palabras, la
intensidad de la señal para ese nucleo no cambia…
• Muy distinto para un espin que se mueve rapido…
Gradientes y difusion (continuado)
y
y
G(δ)
x
x
y
180
Δ/2
y
-G(δ)
x
Δ/2
x
• En este caso, y como el nucleo se mueve lejos de donde
estaba originalmente, el gradiente decodificador tiene un
efecto completamente distinto (i.e., continua el desfasaje). En
suma, la intensidad de la señal va a terminar muy atenuada.
• El resultado final es que cuanto mas se muevan los espines,
mas pequeñas seran las señales en el espectro. Elijiendo
bien los valores de G, δ, y Δ podemos ajustar el experimento
para estudiar difusividades de hasta 10-12 m2s-1 (en un Bruker
como el de Malvin Norte).
Gradientes y difusion (continuado)
• Para calcular el valor de D, repetimos el experimento con
muchos valores de G manteniendo δ y Δ constantes.
• La variación de intensidad contra gradiente que se obiente
guarda la siguiente relacion, y un regresion nos da el D.
I(G) = Io x e
[–γ2G2δ2D x (Δ – δ / 3)]
• Datos reales para el [Emim][OAc] a 40 oC:
y = m1*exp(-10000*m2*(2*pi*4...
Value
Error
m1
1.0048
0.0017074
m2
1.5413e-14
6.2518e-17
Chisq 0.00016229
NA
R
0.99995
NA
1.2
1
N
N
y = m1*exp(-10000*m2*(2*pi*4...
Value
Error
m1
0.61144 0.00088819
m2
1.7099e-14
5.8874e-17
Chisq
4.1973e-5
NA
R
0.99997
NA
CH3
0.8
Intensity
H3C
O
H3C
O
0.6
0.4
0.2
0
0
5
10
15
20
Gz (G/cm)
25
30
35