cálculo pérdidas de energía

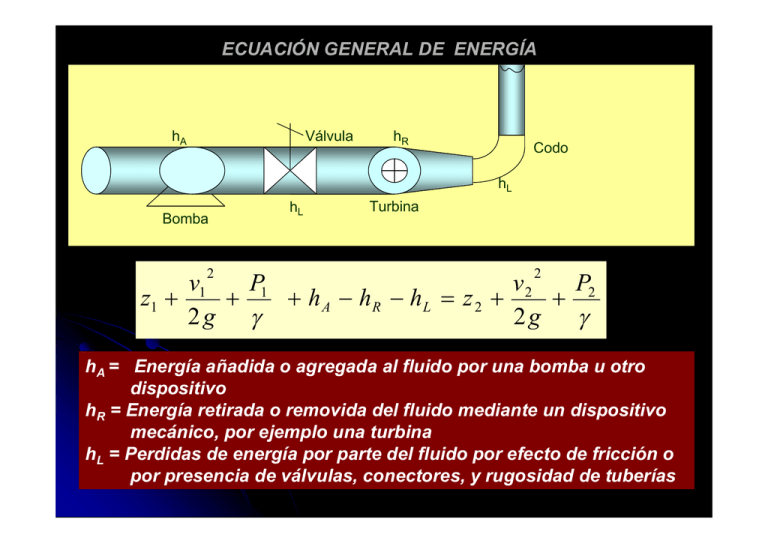
ECUACIÓN GENERAL DE ENERGÍA
Válvula
hA
hR
Codo
hL
Bomba
2
hL
Turbina
2
v1
P1
v2
P2
z1 +
+
+ h A - h R - hL = z 2 +
+
2g g
2g
g
hA = Energía añadida o agregada al fluido por una bomba u otro
dispositivo
hR = Energía retirada o removida del fluido mediante un dispositivo
mecánico, por ejemplo una turbina
hL = Perdidas de energía por parte del fluido por efecto de fricción o
por presencia de válvulas, conectores, y rugosidad de tuberías
PÉRDIDAS DE ENERGÍA hL
Las pérdidas totales de energía hL es dada por
hL = å perdidas por accesorios + å perdidas por fricción en tuberías
Las pérdidas de energía por accesorios = se dan por
cambios de dirección y velocidad del fluido en válvulas te,
codos, aberturas graduales y súbitas entre otros
Las pérdidas por fricción = se dan por el contacto del fluido
con las paredes de las tuberías y conductos que por lo
general son rugosos
Pérdidas de energía debido a la fricción hf
Es dada por la ecuación de Darcy (utilizada para flujo laminar y
turbulento)
L v2
hf = f
D 2g
Donde:
L = longitud de la tubería
D = Diámetro nominal del conducto
V = Velocidad de flujo
f = coeficiente de fricción ( adimensional )
Como obtener el coeficiente de fricción f
Para calcular el coeficiente de fricción “f” se usa el
diagrama de Moody, el cual se presenta en la figura 9-2, o
las siguientes ecuaciones.
Para flujo laminar y tuberías sin rugosidad f= 64/ Re
Para flujo turbulento usar mejor la ecuación de P.K.
SWANCE y A.K. JAIN.
f =
0 , 25
é
1
5 , 74
æ
ê log ç 3 , 7 D / e + Re 0 , 9
è
ë
öù
÷ú
øû
2
Pérdidas por accesorios hl
kv 2
hl =
2g
Donde
hl = perdida menores
k = coeficiente de resistencia
v = velocidad promedio
k = El coeficiente de resistencia es medido experimentalmente y
depende del tipo de accesorio y de la velocidad promedio
CALCULO DE LAS PÉRDIDAS MENORES:
l
Dilatación súbita: depende de la diferencia D1/D2.
ver grafico 10-2 del libro Robert Mott.
D1, V1
D2, V2
D2/D1 vs K para calcular
2
é
ù
é
æ D1 ö ù
æ A1 ö
÷÷ ú
÷÷ ú = ê1 - çç
k = ê1 - çç
êë
è D 2 ø úû
è A2 øû
ë
2
2
K.
Pérdidas menores
Pérdida de entrada a un tanque
D1,
V1
hl
D2, V2
æ v12 ö
hl = 1çç ÷÷
è 2g ø
æv ö
Gradual
1ç ÷
=Dilatación
2
1
ç 2g ÷
è ø
D1,
V1
f,
V2
D2,
æ v12 ö
hl = k çç ÷÷
è 2g ø
Ver grafico 10-5 D2/D1 vs K y f
Perdidas mínimas para f< 7, cuando f> la perdida aumenta, ver tabla 10-2
Pérdidas menores
Concentración súbita
D1, V1
D2, V2
æ v22 ö
hl = k çç ÷÷
è 2g ø
ver figura 10-7 y tabla 10-3
Concentración gradual
D1, V1,
f
D2, V2
para Re >1X105 utilizar la figura 10-10 donde D1/D2 vs K y f
æ v 22 ö
hl = k çç ÷÷
è 2g ø
Pérdidas menores en curvaturas de tuberías
Codos de tuberías
La resistencia al flujo en un codo es función del radio (r ) de la curvatura
del codo y del diámetro interno D.
Donde:
r= es la distancia al centro de la curvatura
Ro= es el diámetro externo del conducto o tubo
Ri
r
Ro
D
Do
r=Ri + Do/2
r=Ro – Do/2
r = (Ro + Ri)/2
Ver grafico 10-23 se puede calcular hl = f (k, le/g)
OTRAS PÉRDIDAS MENORES A LA SALIDA Y ENTRADA
DE UNA TUBERIA EN UN TANQUE
Perdida hacia dentro k =1
Perdida cuadrada
k =0,5
Perdida achatada
k =0,25
Perdidas redonda
r/D2
k
0
0,02
0,04
0,10
> 0,15
0,50
0,28
0,24
0,09
0,04
El coeficiente de resistencia para válvulas es calculado de la siguiente
manera:
hl
Donde
æ v 12 ö
÷÷
= k çç
è 2g ø
k = (le / D) fr
le/D= Longitud equivalente
fr= factor de fricción en el conducto en completa turbulencia
Ver tabla 10-4. del libro Robert Mott.
PÉRDIDAS DE ENERGÍA POR FRICCIÓN
EN CONDUCTOS NO CIRCULARES
Reemplazar en la ecuación de Darcy
Se obtiene entonces
2
L v
hf = f
4R 2g
D=4R