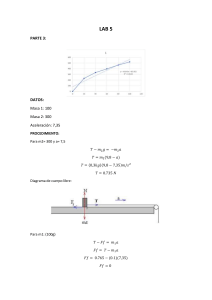
Considere una capa límite turbulenta en una placa plana. Supongamos que solo se conocen dos cosas: 𝐶𝑓,𝑥 ≅ 0,059 ∗ (𝑅𝑒𝑥 )−1/5 y 𝜃 ≅ 0.097 ∗ 𝛿 Utilice la ecuación integral de Kármán para generar una expresión para 𝛿/𝑥, y compare su resultado con la columna (b) de la tabla 10-4. Analizando: Capa Limite: es la zona donde el movimiento de este es perturbado por la presencia de un sólido con el que está en contacto. La capa límite se entiende como aquella en la que la velocidad del fluido respecto al sólido en movimiento varía desde cero hasta el 99% de la velocidad de la corriente no perturbada La capa límite turbulenta generada por el flujo sobre una placa plana COEFICIENTE DE FRICCIÓN LOCAL 𝑪𝒇,𝒙 : Coeficiente de fricción cutánea - coeficiente de fricción local - coeficiente de fricción de piel 𝐶𝑓,𝑥 = 1 2 τ𝑤 ∗ 𝜌 ∗ 𝑈2 𝝆: es la densidad de un fluido 𝑼 : es la velocidad de la corriente libre, que es la velocidad del fluido lejos de la superficie del cuerpo. 𝛕𝒘 : es un esfuerzo cortante de la piel en una superficie o en variables físicas (Tenciones en la pared) 𝟏 ∗ 𝟐 𝝆 ∗ 𝒗𝟐 ∶ es la presión dinámica de una corriente libre τ𝑤 = 0.332 ∗ 𝜌 ∗ 𝑈2 √𝑅𝑒𝑥 𝑹𝒆𝒙 : es el número de Reynolds. X: es la distancia desde el punto de referencia en el que comienza a formarse una capa límite. 𝐶𝑓,𝑥 = 0.664 √𝑅𝑒𝑥 La relación muestra que nuestro coeficiente de fricción disminuye a medida que el número de Reynolds "𝑅𝑒𝑥 " aumenta ESPESOR DE LA CANTIDAD DE MOVIMIENTO Otra medición del espesor de la capa limite es el espesor de la cantidad de movimiento, a la que comúnmente se le asigna el símbolo”𝜃” ∞𝑢 𝜃 = ∫0 𝑈 𝑢 (1 − 𝑈) 𝑑𝑦 Por dato 𝜃 = 0.097 ∗ 𝛿 Expresado para una placa, capa limite laminar 𝜃 0.664 = 𝑥 √𝑅𝑒𝑥 ECUACION INTEGRAL DE KARMAN 𝑑 𝑑𝑈 τ𝑤 (𝑈 2 ∗ 𝜃) + 𝑈 ∗ 𝛿^ = 𝑑𝑥 𝑑𝑥 𝜌 𝑈: velocidad del flujo externo a la capa limite 𝜃: espesor de perdida de cantidad de movimiento 𝛿^: espesor de desplazamiento Todas nuestras variables solo dependen de “x” (la coordenada tangencial al cuerpo en la que se desarrolla la capa limite) La velocidad potencial exterior “𝑈" es un dato conocido y (𝜽, 𝜹` 𝒚 𝛕𝒘 ) son las incógnitas de esta ecuación y lo que podemos hacer es intentar obtener una ecuación diferencial de una sola variable. CASO PARTICULAR: Capa limite sin gradiente de presión (para una placa plana) En este caso la velocidad “U” será constante 𝑈(𝑥) = 𝐶𝑡𝑒 = 𝑈 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑑𝑈 =0 𝑑𝑥 reemplazando 𝑑 𝑑𝑈 τ𝑤 (𝑈 2 ∗ 𝜃) + 𝑈 ∗ 𝛿^ = 𝑑𝑥 𝑑𝑥 𝜌 𝑈2 ∗ 𝑑 τ𝑤 (𝜃) = 𝑑𝑥 𝜌 𝑑 τ𝑤 (𝜃) = 𝑑𝑥 𝜌 ∗ 𝑈2 Esta expresión es también "𝐶𝑓,𝑥 " entre 2 𝐶𝑓,𝑥 𝑑 τ𝑤 (𝜃) = = 2 𝑑𝑥 𝜌∗𝑈 2 Solución Debemos encontrar la expresión 𝛿/𝑥 sabemos que podemos despejar 𝛿 del dato de “ 𝜃 “y “x” del número de Reynolds despejando “ 𝐶𝑓,𝑥 ” 𝐶𝑓,𝑥 𝑑 τ𝑤 (𝜃) = = 2 𝑑𝑥 𝜌∗𝑈 2 𝐶𝑓,𝑥 = 2 ∗ 𝑑 𝑑𝑥 ( 𝜃) 𝑑 Debemos obtener la expresión “𝑑𝑥 (𝜃)” para ello vamos a derivar 𝜃 que es dato = 0.097 ∗ δ 𝑑 dδ (𝜃) = 0.097 ∗ 𝑑𝑥 𝑑𝑥 𝑑 Reemplazando “𝑑𝑥 (𝜃)” en nuestra ecuación 𝐶𝑓,𝑥 = 2 ∗ 0.097 ∗ 𝐶𝑓,𝑥 = 0.194 ∗ dδ 𝑑𝑥 dδ 𝑑𝑥 Ahora remplazamos “𝐶𝑓,𝑥 ” que es dato igual a 0,059 ∗ (𝑅𝑒𝑥 )−1/5 0,059 ∗ (𝑅𝑒𝑥 )−1/5 = 0.194 ∗ 0.30412 ∗ (𝑅𝑒𝑥 )−1/5 = dδ 𝑑𝑥 dδ 𝑑𝑥 Reemplazando el numero de Reynolds 𝑅𝑒 = 𝑉∗𝐷 𝑣 𝑉: velocidad del fluido ( U = Cte = v) 𝑣: viscosidad 𝐷: Diámetro interno de la tubería (x) (𝑅𝑒𝑥 )−1/5 = ( 𝑉 ∗ 𝑥 −1/5 ) 𝑣 𝑉 −1/5 Reemplazando en la ecuación “ (𝑅𝑒𝑥 )−1/5 “= (𝑣 ) ∗ (𝑥)−1/5 1 1 𝑉 −5 dδ 0.30412 ∗ ( ) ∗ (𝑥)−5 = 𝑣 𝑑𝑥 𝑉 (0.30412 ∗ ( )−1/5 ∗ (𝑥)−1/5 ) ∗ 𝑑𝑥 = dδ 𝑣 Integramos ambas partes de la expresión para poder despejar “ δ “ 𝑉 ∫ (0.30412 ∗ ( )−1/5 ∗ (𝑥)−1/5 ) ∗ 𝑑𝑥 = ∫ dδ 𝑣 𝑉 0.30412 ∗ ( )−1/5 ∗ ∫((𝑥)−1/5 ) ∗ 𝑑𝑥 = ∫ dδ 𝑣 1 1 𝑉 −5 (𝑥)−5+1 0.30412 ∗ ( ) ∗ = δ 1 𝑣 − +1 5 4 𝑉 (𝑥)5 0.30412 ∗ ( )−1/5 ∗ = δ 4 𝑣 5 4 𝑉 5 0.30412 ∗ ( )−1/5 ∗ ∗ (𝑥)5 = δ 𝑣 4 4 𝑉 0.38015 ∗ ( )−1/5 ∗ (𝑥)5 = δ 𝑣 Nos piden hallar la expresión 𝛿/𝑥 entonces dividimos toda la expresión entre “x” 4 𝑉 0.38015 ∗ ( 𝑣 )−1/5 ∗ (𝑥)5 δ = 𝑥 𝑥 1 𝑉 δ 0.38015 ∗ ( )−1/5 ∗ (𝑥)−5 = 𝑣 𝑥 1 𝑉 δ 0.38015 ∗ ( )−1/5 ∗ (𝑥)−5 = 𝑣 𝑥 𝑉 −1/5 𝑣 Podemos expresar como Reynolds nuevamente (𝑅𝑒𝑥 )−1/5 = ( ) 𝟎. 𝟑𝟖𝟎𝟏𝟓 ∗ (𝑹𝒆𝒙 )−𝟏/𝟓 = ∗ (𝑥)−1/5 𝛅 𝒙 * Los valores laminares son exactos y se enumeran con tres dígitos significativos, pero los valores turbulentos se enumeran solo con dos dígitos significativos debido a la gran incertidumbre relacionada con todos los campos de flujo turbulento. † Obtenido de la ley de la séptima potencia. ‡ Obtenido de la ley de la séptima potencia combinada con datos empíricos para flujo turbulento a través de tubería.