Evolución histórica de las fórmulas para expresar las

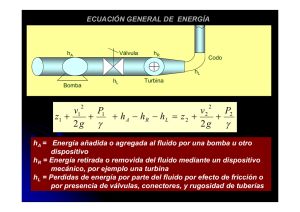
INGENIERÍA HIDRÁULICA Y AMBIENTAL, VOL. XXIII, No. 3, 2002
Evolución histórica de las fórmulas para
expresar las pérdidas de carga en tuberías.
Segunda parte: Desde los trabajos de Darcy
hasta los de Stanton
INTRODUCCIÓN
En un trabajo anterior, 1 se hizo un estudio de la evolución
de las fórmulas para expresar las pérdidas de carga en
tuberías, desde los primeros experimentos conocidos,
realizados por Couplet en 1732, hasta los resultados
publicados por Darcy en 1857, que fue el primero en tener en
cuenta la influencia que ejerce el estado de las paredes
interiores de la tubería en la cuantía de las pérdidas de carga.
También se demostró que la forma de expresar las pérdidas
de carga que se atribuye a Darcy no fue nunca utilizada por
ese investigador. La llamada fórmula de Darcy o de WeisbachDarcy, también conocida como racional se representa por:
hf = f (L/D) (U 2/ 2g)
...(1)
donde:
hf: Pérdidas de carga expresadas en unidades de longitud
f: Coeficiente de fricción (adimensional, función del número
de Reynolds).
L: Longitud de la tubería.
D: Diámetro interior de la tubería.
U: Velocidad media de circulación en la tubería.
g: Intensidad de la gravedad.
Es justo llamar fórmula de Weisbach a la ecuación (1), ya
que en 18452 este investigador publicó un manual en que
aparecía la fórmula expresada en la forma hoy conocida y
encontró además que el coeficiente de fricción variaba no
solo con la velocidad, sino también con el diámetro y el
material de la pared de la tubería.
Darcy escogió para representar los resultados de sus
experimentos, la forma monómica:
rJ = b1U 2
Resumen / Abstract
Partiendo de los trabajos de Darcy, que señalaron por primera
vez la influencia que ejerce el estado de las paredes interiores de
las tuberías sobre las pérdidas de carga, se examinan una serie de
fórmulas propuestas por distintos investigadores. Pero fue Osborne
Reynolds (1883), el que al fin abrió el camino al tratamiento
científico del problema, al reconocer la existencia del flujo laminar
y el turbulento, fijar sus límites y utilizar el análisis dimensional
para proponer una fórmula racional para expresar la resistencia
al flujo en conductos. Se analizan gran número de fórmulas
propuestas por diversos investigadores. Sin embargo, no es hasta
que Blasius (1913) y Stanton (1914), relacionan el coeficiente de
fricción, f, de la fórmula de Weisbach-Darcy, con el número de
Reynolds y la rugosidad de la tubería, que se inicia un nuevo
camino en el análisis racional de las pérdidas de carga en las
conducciones a presión.
Palabras clave: fórmulas de pérdidas; pérdidas de carga; flujo
en tuberías; historia de la Hidráulica
Starting from the experimental results of Darcy that demonstrated
by the first time tuhe influence of the internal surface of the pipes
upon the loss of head, several formulas proposed by different
investigators are examined. But it was Osborne Reynolds (1883),
the one that opened the way tothe scientific treatment of the subject,
by recognizing the existance of laminar and turbulent flow, fixing
their limits and utilizing the dimensional analysis for the
development of a rational equation for representing the resistance
to flow in conduits. A great number of formulas proposed by
different investigators after Reynolds are analyzed. Nevertheless,
a new way in the rational analysis of the losses of head in
pressurized conduits was initiated by Blasius (1913) and Stanton
(1914), by relating f, the friction coefficient of Weisbach-Darcy
formula wituh the Reynolds number and the internal roughness of
pipes.
Key words: loss of head formulas; head losses; pipe flow; history
of Hydraulics
...(2)
Diosdado Pérez Franco, Profesor Titular, Doctor en Ciencias, Ingeniero Hidráulico, Centro de Investigaciones Hidráulicas, CIH,
Instituto Superior Politécnico José Antonio Echeverría, CUJAE, Ciudad de La Habana
e-mail: [email protected]
3
donde:
r: Radio interior de la tubería.
J: Rasante hidráulica.
b1: Coeficiente.
El coeficiente b1 está expresado por la ecuación
b1 = α + β/r
permite escribir:
hf = (Q/20 )2 ( 1/D )5 L
...(3)
o sea, que está formado por un elemento constante, α, y
otro expresado por β/r que varía en razón inversa del radio
de la tubería.
Teniendo en cuenta los valores de b1 que encontró
experimentalmente en tubos nuevos, cuyos diámetros
variaban desde 0,012 2 m hasta 0,5 m, Darcy determinó
que:
b1 = 0,000 507 + (0,000 006 47/r)
...(4)
lo que permite expresar la fórmula realmente propuesta
por Darcy, para tubos nuevos, enj función del diámetro,
como:
DJ = [0,001 014 + ( 0,000 025 88/D)] U2
...(5)
Después de Darcy diversos investigadores continuaron
realizando experimentos, pero fue Osborne Reynolds con
la publicación de sus resultados en 1883, el que al fin
abrió el camino al tratamiento científico del problema, al
reconocer la existencia del flujo laminar y el turbulento,
fijar sus límites y utilizar el análisis dimensional para
proponer una fórmula racional para expresar la resistencia
al flujo en conductos. Debe reconocerse, en justicia, que
ya Hagen en 1839 había hecho la primera advertencia de
la existencia de dos regímenes diferentes de flujo. 2
Sin embargo, no es hasta que Blasius en 19132 y
Stanton en 1914, relacionan el coeficiente de fricción, f,
de la fórmula de Weisbach-Darcy, con el número de
Reynolds y la rugosidad de la tubería, que se inicia un
nuevo camino en el análisis racional de las pérdidas de
carga en las tuberías.
DESDE DARCY HASTA REYNOLDS
A partir de los trabajos de Darcy, numerosos
investigadores continuaron proponiendo nuevas fórmulas
para expresar las pérdidas de carga. Así, Dupuit en 1865,
señala, que como la velocidad no es ordinariamente una
cantidad conocida ni buscada, utilizará en su lugar el
caudal, Q, en la forma monómica de la fórmula y propone
para calcular las pérdidas una expresión, que en nuestra
notación queda como:
hf = CD (L/D5) Q2
...(6)
donde, CD , es un coeficiente numérico, cuyo valor más
conveniente de acuerdo con el estado de la ciencia en
ese momento, según Dupuit, era de 0,002 5, lo que
4
...(7)
que a su vez puede transformarse para expresarla en la
forma acostumbrada en la época, en:
J = (4/D) . 0,385 5 . 10-3 U 2
...(8)
En 1867, M. Levy en su "Theorie d'un courant liquide",3
propuso las siguientes fórmulas en metros y segundos:
Para tuberías de hierro fundido nuevas:
U = 36,4 [rJ (1+ r1/2)] 1/2
...(9)
Para tuberías de hierro fundido en servicio:
U = 20,5 [rJ(1 + 3r1/2)] 1/2
...(10)
A las cuales añadió Vallot en 1888, para tuberías de
hierro fundido que se hayan limpiado:
U = 32,5 [rJ (1 + r1/2)] 1/2
...(11)
En 1873, Lampe (citado por Forchheimer y Bovey, 3,4
basándose en sus propios experimentos, propuso la
fórmula:
D1,25 J = aL U1,802
...(12)
donde aL es un coeficiente de fricción.
Según Gibson, 5 Hagen en 1854, había deducido de los
experimentos de Couplet, Bossut y Dubuat una fórmula
que expresada en nuestra notación, resulta:
hf = f H (L/D1,25) U1,75
...(13)
Donde f H , es un coeficiente de fricción. Pero no descubrió
ninguna ley de variación de los exponentes, ni del
coeficiente de fricción, con el estado de la superficie interior
ni el diámetro del tubo.
Posteriormente, según señala Bovey, 3 el propio Hagen
propuso la fórmula:
hf/L = aH (U n / D x )
...(14)
donde los coeficientes aH, n y x , dependían de la
velocidad, el diámetro y la rugosidad relativa de la tubería.
Según Forchheimer, 4 la gran disparidad de criterios
respecto a la fórmula adecuada para determinar las pérdidas
de carga en las tuberías, decidió a la Asociación de
Arquitectos e Ingenieros Alemanes a recopilar experiencias
en relación con el tema, información que permitió a O.
Iben en 1880, llegar a la conclusión de que para tuberías
limpias, la fórmula propuesta por Darcy era la que mejor
expresaba los resultados experimentales y que no podía
establecerse una ley de carácter general para el aumento
de la resistencia con el tiempo, a causa de la variedad e
irregularidad de los sedimentos.
En 1883, Osborne Reynolds, 6 desarrolló a través del
análisis dimensional una ley racional de resistencia al flujo,
basándose en la suposición de que la resistencia dependía
del diámetro, la longitud, y la condición de la superficie
interior de la tubería; de la viscosidad y densidad del fluido
y de la velocidad media del flujo a través de la tubería y
también que dependía de cierta potencia de cada uno de
esos elementos.
La fórmula de Reynolds, válida para tubos capilares y
de mayor diámetro, o sea, para flujo laminar y turbulento,
según la presenta Gibson, puede expresarse en nuestra
notación como:
hf = k Un ν 2 -n L D n-3
...(15)
donde:
n: Exponente de la velocidad media del flujo.
k: Coeficiente que depende de la rugosidad de la tubería.
ν: Viscosidad cinemática del fluido.
Un análisis de la ecuación (15) permite deducir, que
cuando los experimentos indican que las pérdidas varían
con el cuadrado de la velocidad (n = 2), la viscosidad
cesa de tener efecto, y resultará que:
hf = k (L/D) U 2
...(16)
De acuerdo con los resultados experimentales de
Reynolds, n =1 cuando no se excede la velocidad crítica
(límite superior del flujo laminar) y varía de 1,7, para tubos
lisos, a 2, para tubos muy rugosos, para valores de la
velocidad mayores que la crítica (flujo turbulento).
Reynolds señala además, que en la ecuación (15) la suma
de los exponentes de D y de U, es siempre 3.
La expresión exponencial de Reynolds permite expresar
en esa forma los resultados de los experimentos de otros
investigadores anteriores y posteriores a él, y puede
representarse como una línea recta en un diagrama
logarítmico de hf/L vs U.
Reynolds analizó las experiencias de Darcy y constató
que también podían ser representadas por líneas rectas
en gráficos logarítmicos deduciendo de ello, según
Forchheimer, que para:
Tubos de vidrio
Tubos de plomo unidos por soldadura
Tubos de hierro dulce asfaltados
Tubos nuevos de fundición
Tubos con incrustación
Tubos desincrustados
n=
n=
n=
n=
n=
n=
1,79
1,79
1,82
1,88
2
1,91
DISTINTAS FORMAS ADOPTADAS PARA EXPRESAR
LAS FÓRMULAS DE PÉRDIDAS DE CARGA
EN TUBERÍAS
Al analizar las diversas formas en que pueden
presentarse las ecuaciones de pérdidas de carga, por
costumbre, se han ido prefiriendo dos tipos principales:
a) las pérdidas expresadas en función de la velocidad, tal
como aparecen en las ecuaciones (1) y (15): y b) la
velocidad expresada en función de la rasante hidráulica
tal como aparece en las que se basan en la expresión
propuesta por Chezy en 1775 para el flujo en canales,7,2
o sea:
U = CCH (RJ)1/2 = CCH (DJ/4)1/2
...(17)
donde:
CCH : Coeficiente de Chezy.
R: Radio hidráulico del conducto.
Para darle unidad al análisis que se está haciendo, es
en esas dos formas que se presentarán los resultados de
los investigadores posteriores a Reynolds, independientemente de la forma original en que los hayan
presentado.
Todas las fórmulas exponenciales pueden expresarse
como casos particulares de la expresión general:
U = C Rx J y
...(18)
donde:
C: Coeficiente de fricción.
x: Exponente del radio hidráulico o del diámetro.
y: Exponente de la rasante hidráulica.
FÓRMULAS EXPONENCIALES POSTERIORES
A REYNOLDS
Unwin (Gibson, 1925) basándose en que cuando n = 2,
en la fórmula de Reynolds (ecuación 15), las pérdidas
varían según una potencia del diámetro mayor que uno,
escribió la fórmula, sin tener en cuenta los efectos de la
temperatura, en la forma siguiente:
hf = f U L U n D -x
...(19)
donde:
f U : Coeficiente de fricción.
n: Exponente de la velocidad.
x: Exponente del diámetro.
Unwin dedujo valores para el coeficiente y los
exponentes, a partir de los resultados de los experimentos
realizados por varios investigadores, para tuberías desde
2 hasta 48 pulgadas de diámetro (1 pulgada = 2,54 cm). De
acuerdo con sus observaciones, resulta siempre mayor
que uno, y aumenta con el diámetro entre los límites 1,127
y 1,390.
5
Edgard Thrupp (citado por Gibson, Bovey y Flamant)3,5,8
propuso en 1887 otra modificación de la fórmula de
Reynolds, como sigue:
hf = CT (L/R x) U n
...(20)
donde:
CT: Coeficiente de fricción.
En 1889, C. H. Tutton (citado por Forchheimer y Bovey)
después de realizar gran número de ensayos, encontró,
que en general para las fórmulas expresadas como la
ecuación 18, la suma x + y = constante = 1,17 , mientras
que esa suma según Reynolds debe oscilar entre 1 y 1,35.
Es decir que la fórmula de Tutton queda como:
U = C R 1,17-y Jy
...(21)
Así resulta, que para y = 0,5 , la fórmula de Tutton se
transforma en:
U = C R 0,67 J 0,5
...(22)
que como se verá mas adelante, es equivalente a la fórmula
de Manning.
A. Flamant en 18924,8 basándose en los trabajos de
numerosos investigadores que le precedieron propuso la
fórmula:
D 5 J 4 = aF 4 U 7
...(23)
que puede expresarse también como:
U = a F 4/7 D5/7 J 4/7 = λ D 5/7 J 4/7
...(24)
donde:
af y λ son coeficientes numéricos que dependen del
sistema de unidades que se utilice. Para unidades del
SI (m y s) según Forchheimer λ tiene los siguientes valores:
Para tubos de plomo, vidrio y palastro
λ = 68,1 a 75,3
Para tubos de fundición nuevos
λ = 61,5
Para tubos usados
λ = 54,3
Flamant señala que los efectos de las incrustaciones
son variables con el diámetro del tubo y resultan menores
según aumenta el diámetro de la tubería. Por otra parte,
plantea, que los tubos perfectamente lisos son una
excepción y que es raro que conserven por mucho tiempo
su pulimento primitivo; que se puede ver, de acuerdo con
las observaciones de Darcy, que un depósito apenas
perceptible, de una pequeña fracción de milímetro de
espesor, es suficiente para cambiar las condiciones de
escurrimiento y aumentar la resistencia, por lo que él
propone adoptar para todos los casos prácticos, la
fórmula:
7
1/4
D J = 0,000 92 (U /D)
6
...(25)
Según advierte Fanning9 es deseable tener una fórmula
general en forma exponencial que pueda utilizarse sin una
tabla o diagrama de coeficientes. En ese intento, Fanning
partiendo de la fórmula de Hagen (ecuación 13) y
suponiendo un valor constante para el coeficiente aH en
cada caso, determinó una fórmula con distintos
exponentes para cada tipo de tubo correspondiente a una
clasificación en doce clases que dependían del tipo de
material de que estaban construidos y de las condiciones
de su superficie interna.
Aunque originalmente desarrolladas para canales
abiertos, algunas fórmulas exponenciales de ese tipo,
también se han utilizado para tuberías, tales como la de
Ganguillet y Kutter y la de Manning. 8,9
Los ingenieros suizos Ganguillet y Kutter propusieron
en 18694 para determinar el valor de la C de Chezy, la
expresión:
1 0,00155
+
n
J
CCH =
0,00155 2n

1+  23 +

J

 D
23 +
...(26)
donde:
n: Coeficiente de rugosidad.
Esta fórmula puede utilizarse para tubos fundidos en
servicio, dándole a n un valor de 0,011 ó 0,012, o sea,
utilizando como promedio 1/n = 88. La fórmula de Kutter
se ha utilizado mucho para pérdidas de carga en tuberías,
especialmente en Europa.
Otra fórmula desarrollada inicialmente para canales, que
se ha usado mucho con tuberías es la propuesta por Robert
Manning en 1890, que se expresa en unidades del SI,
como:
U = (1/n) R 2/3 J 1/2
...(27)
que para C = 1/n coincide con la fórmula de Tutton
modificada (ecuación 22).
Strickler en 192310 propuso hacer 1/n = 21,1/e1/6 ,
donde e representa el espesor de la rugosidad de la
pared. En esa forma, se usa mucho en Europa,
denominándola fórmula de Manning-Strickler. Al utilizar
esta fórmula debe tenerse en cuenta, que es para
régimen turbulento y que no es aplicable a tubos lisos
o virtualmente lisos.
Saph y Schoder11 en 1903, desarrollaron una fórmula
exponencial para tuberías de pequeño diámetro,
menores de dos pulgadas, respaldada por numerosos
experimentos, que puede expresarse para la mayoría
de los casos, como:
H=
0,296 a 0,469 1,74 a 2,00
U
D1,25
...(28)
donde:
H: Pérdidas de carga expresadas en pies por cada mil
pies y D y U están expresadas en pies y pies por segundo
respectivamente.
Una de las fórmulas exponenciales más populares, sobre
todo en las Américas, es la de Williams-Hazen, 12 utilizada
desde 1902, respaldada por experimentos de los autores
y por los trabajos de sus predecesores, que expresada en
pies y segundos, resulta:
U = 1,318 CWH R0,63 J 0,54
...(29)
Y en metros y segundos:
U = 0,849 CWH R 0,63 J 0,54
...(30)
donde:
CWH: Coeficiente de resistencia o de fricción de WilliamsHazen.
El coeficiente C WH es un índice de la lisura de la
superficie interior de la tubería. El exponente de R, indica
la razón de aumento en velocidad con el radio hidráulico ó
el diámetro a pendiente constante. El exponente de J,
indica la razón a que crece la fricción con la velocidad.
Los valores del coeficiente de fricción dependen del
material de la tubería y de la edad, es decir, del tiempo
que haya estado en servicio la tubería. Los autores
advierten que su fórmula no debe usarse para tubos
menores de una pulgada (2,54 cm), y que en ese caso es
mejor utilizar la de Saph y Schoder.
Como se puede observar, la fórmula de Williams-Hazen,
cumple el requisito de que la suma de los exponentes de
R y J es 1,17.
La fórmula de Williams-Hazen también puede
expresarse en unidades del sistema internacional, como: 13
hf = (6,822/C1,852) (L/D1,167) U 1,852
...(31)
y en función del caudal:
hf = (10,679/C1,852) (L/D 4,87) Q1,852
...(32)
donde:
C = CWH
Para aplicar su fórmula, Williams y Hazen prepararon
reglas de cálculo y tablas, que a nuestro entender, han
contribuido a la preferencia que se ha tenido en su utilización
antes de existir las calculadoras científicas.
COEFICIENTE DE FRICCIÓN EN LA FÓRMULA
DE WEISBACH-DARCY
Según Hughes and Safford, Harris y Rouse, 2,14,15 entre
otros, la forma de la fórmula de pérdidas de carga atribuida
a Darcy fue presentada por primera vez por Weisbach.
También se le conoce como fórmula de Fanning, sobre
todo en el campo de la Ingeniería Química. 16
En efecto, Fanning en su libro, cuya primera edición se
hizo en 1876, al analizar la resistencia al flujo en las
tuberías, presentó como fórmula básica, que expresada
en su notación original:
R =
C
S
×l ×m ×
V2
2g
...(33)
donde:
R: Carga equivalente a la resistencia al flujo (pies).
C: Perímetro de la circunferencia del tubo (pies).
S: Área de la sección interior del tubo (pies cuadrados).
l: Longitud del tubo ( pies).
V: Velocidad media del flujo (pies por segundo).
g: Intensidad de la gravedad (pies/s2).
m: Coeficiente de flujo.
Fanning señala, que el coeficiente m es un nuevo
coeficiente de flujo que debe ser investigado
experimentalmente y que no debe confundirse con otros
coeficientes investigados hasta el momento e indica que
el valor de m es variable.
Para investigar el valor de m, propone usar los
experimentos de los investigadores que le precedieron y
prepara tablas para los valores de m para distintos
diámetros y velocidades de circulación, tomando como
base los experimentos de Hamilton Smith Jr.,Darcy, él
mismo, Dubuat, Bossut, Couplet, Provis, Rennie, Greene,
Bailey y otros. Observa que en general, el coeficiente m
decrece según aumenta el diámetro o el radio hidráulico y
que, para un diámetro fijo el coeficiente disminuye según
aumenta la velocidad. También se constata, que en
igualdad de otras condiciones, el valor de m crece con la
mayor incrustación del tubo.
Teniendo en cuenta que la relación S/C en la ecuación (33) representa el radio hidráulico, dicha ecuación, o
sea la fórmula de Fanning expresada en la notación
utilizada en este trabajo, quedará como:
hf = m (L/R) (U 2 /2g)
...(34)
y recordando, que para un conducto circular con flujo a
presión, R = D/4, la fórmula de Fanning se transformará
en:
hf = 4 m (L/D) (U 2 / 2g)
...(35)
que comparada con la ecuación (1), permite decir que:
f=4m
...(36)
O sea, que el coeficiente f de la llamada fórmula de
Darcy es cuatro veces mayor que el coeficiente m de la
fórmula de Fanning.
7
Si se despeja el valor de U en la ecuación (34), resulta:
1/ 2
 2gRhf 
U =

 mL 
1/ 2
 2g 
= 
m 
(RJ)1/ 2
...(37)
ecuación, que comparada con la (17), establece la
equivalencia entre los coeficientes de Chezy y de Fanning,
o sea :
CCH =
2g
m
...(38)
A partir de los experimentos de Reynolds se encontró
que el valor del coeficiente de fricción, f, estaba controlado
por el producto de la velocidad y cualquier dimensión lineal
de la sección transversal del conducto. En esa línea se
definió posteriormente el número de Reynolds, NR, como:
NR = U D ρ / µ = U D/ν
...(39)
Se puede demostrar que el factor adimensional f ,
depende del valor de NR y de la rugosidad relativa, e/D,
donde e representa la rugosidad absoluta.
Fue Blasius en 19132 el que primero representó los
valores de f en función del NR en un diagrama doble
logarítmico, para tuberías lisas, producto de un análisis
de las mediciones de resistencia realizadas por Saph y
Schoder. Estos resultados quedaron representados por la
siguiente fórmula empírica, válida hasta NR = 100 000.
f = 0,316/NR0,25
...(40)
Stanton17 en 1914 representó en la misma forma, los
resultados de experimentos con tubos lisos, así como,
con tuberías de hierro fundido limpio y de acero liso. Esta
forma de representar los valores de f en función del NR se
conoce desde entonces como diagrama de Stanton.
Blasius y Stanton, al relacionar f con el NR, para
determinadas condiciones de la superficie de la pared
interior de las tuberías, resolvieron al menos en parte el
dilema que se presentaba cada vez que aparecía una nueva
serie de mediciones y despejaron el camino para posibilitar
un análisis más racional de las pérdidas de carga en
tuberías.
CONCLUSIONES
Como se ha señalado, fue Darcy en 1857, el primero
que tuvo en cuenta la influencia del estado de las paredes
interiores de las tuberías en la cuantía de las pérdidas de
carga. A partir de este conocimiento fundamental
numerosos investigadores propusieron fórmulas para
expresar las pérdidas de carga en las tuberías. Pero fue
Osborne Reynolds con la publicación de sus resultados
en 1883, el que abrió al fin el camino al tratamiento científico
del problema, al reconocer la existencia del flujo laminar y
el turbulento, fijar sus límites y utilizar el análisis
dimensional para proponer una fórmula racional para
expresar la resistencia al flujo en conductos.
8
Sin embargo, no es hasta que Blasius en 1913 y Stanton
en 1914, relacionan el coeficiente de fricción, f, de la
fórmula de Weisbach-Darcy con el número de Reynolds y
la rugosidad de la tubería, que se inicia un nuevo camino
en el análisis racional de las pérdidas de carga en las
tuberías. A partir de esa fecha, la relación antes
mencionada, se comienza a representar en gráficos doble
logarítmicos, conocidos posteriormente como diagramas
de Stanton.
REFERENCIAS
1. PÉREZ FRANCO, DIOSDADO: "Evolución histórica de
las fórmulas para expresar las pérdidas de carga en
tuberías. Primera parte: Desde los experimentos de
Couplet hasta los de Darcy". Ingeniería Hidráulica y
Ambiental, Vol. XXII, No. 2, 2001.
2. ROUSE, HUNTER Y SIMON INCE: History of
Hydraulics. Dover Publications Inc., New York, 1963.
3. BOVEY, HENRY T.: A Treatise on Hydraulics, Second
Edition, John Wiley and Sons, New York-London
Chapman and Hall Limited, 1909.
4. FORCHHEIMER, PHILIPP: Tratado de Hidráulica.
Reimpresión, Editorial Labor S. A., Barcelona, Madrid, 1950.
5. GIBSON A. H.: Hydraulics and its applications, Third
edition, D. Van Nostrand Company, New York, 1925.
6. REYNOLDS, OSBORNE: "An Experimental Investigation
of the Circumstances which Determine Wether the Motion
of Water Shall be Direct or Sinuous and of the Law of
Resistance in Parallel Channels". Philosophical
Transactions of the Royal Society, Vol. 174, 1883.
7. PRINCE, GEORGE T.: Tabulated Data with Explanatory
Notes Relating to Flow of Water Under Pressure
Through Clean Closed Conduits, D. Van Nostrand
Company, New York, 1916.
8. FLAMANT, A.: Hydraulique, Troisieme edition, Librairie
Polytechnique, Ch. Beranger, Editeur, Paris, 1909.
9. FANNING, J. T.: A Practical Treatise on Hydraulics and
Water Supply Engineering, Fifteenth Edition, D. Van
Nostrand Company, New York, 1902.
10. JAEGER, CHARLES: Engineering Fluid Mechanics,
Blackie and Son Limited, London, Glasgow, 1956.
11. SAPH, AUGUSTUS V. Y ERNEST H. SCHODER: "An
Experimental Study of the Resistance to the Flow of
Water in P ipes". Transactions ASCE, Vol. LI,
Transaction paper, No. 964, pp. 253-330, 1903.
12. WILLIAMS, GARDNER S. Y ALLEN HAZEN: Hydraulic
tables, Third edition, revised, John Wiley and Sons,
New York, 1920.
13. PÉREZ FRANCO, DIOSDADO: Introducción al estudio
de los sistemas de tuberías , Primera reimpresión, Editorial
Pueblo y Educación, Ciudad de La Habana, 1986.
14. HUGHES, HECTOR J. Y ARTHUR T. SAFFORD:
Hydraulics. The Mac Millan Company, New York, 1926.
15. HARRIS, CHARLES W.: Hydraulics, John Wiley and
Sons, New York, 1936.
16. GONZÁLEZ DEL TÁNAGO, JOSÉ: Fluidodinámica y
transporte de fluidos en sus aplicaciones a la Ingeniería
Química, Editorial Dossat S. A., Madrid, 1953.
17. STANTON, T. E. Y J. R. PANNELL: "Similarity of Motion
in Relation to the Surface Friction of Fluids". Proc. Royal
Society, London, v. A 214, pp. 199-224, 1914.
Recibido: febrero del 2002
Aprobado: mayo del 2002