Graficación de funciones cuadráticas usando la forma estándar

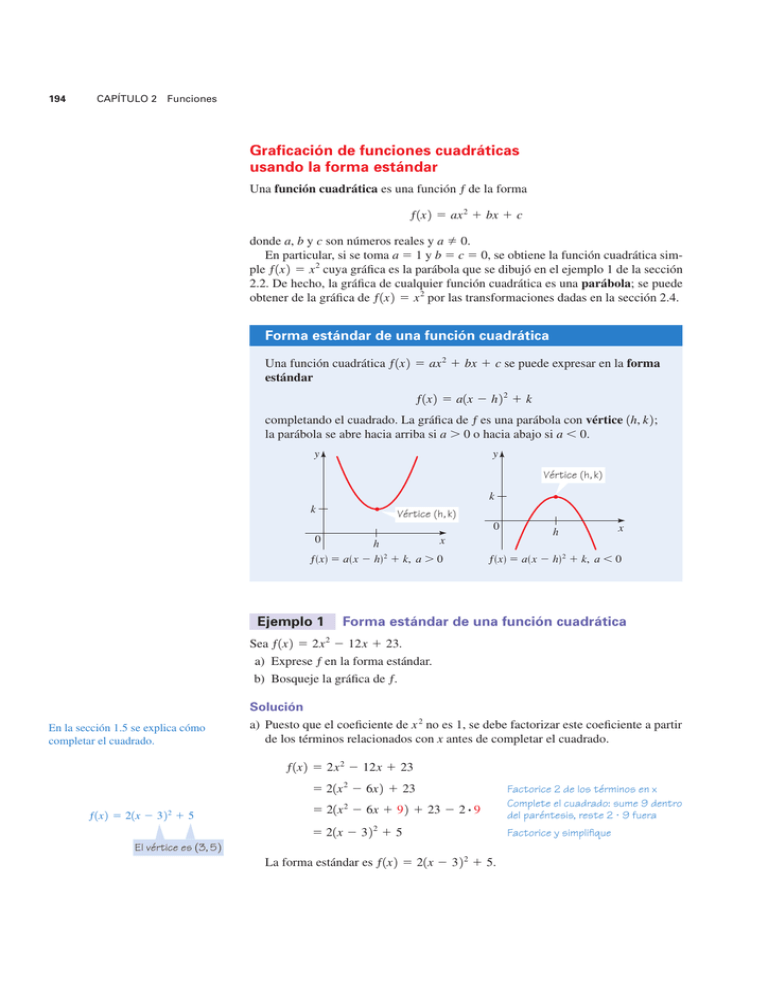
194
CAPÍTULO 2 Funciones
Graficación de funciones cuadráticas
usando la forma estándar
Una función cuadrática es una función f de la forma
f 1x2 5 ax 2 ! bx ! c
donde a, b y c son números reales y a 0.
En particular, si se toma a 5 1 y b 5 c 5 0, se obtiene la función cuadrática simple f 1x2 5 x 2 cuya gráfica es la parábola que se dibujó en el ejemplo 1 de la sección
2.2. De hecho, la gráfica de cualquier función cuadrática es una parábola; se puede
obtener de la gráfica de f1x 2 5 x 2 por las transformaciones dadas en la sección 2.4.
Forma estándar de una función cuadrática
Una función cuadrática f 1x2 5 ax 2 ! bx ! c se puede expresar en la forma
estándar
f 1x2 5 a1x $ h 2 2 ! k
completando el cuadrado. La gráfica de f es una parábola con vértice 1h, k2 ;
la parábola se abre hacia arriba si a " 0 o hacia abajo si a # 0.
y
y
Vértice (h , k)
k
k
Vértice (h , k)
0
0
x
h
Ï=a(x-h)™+k, a>0
Ejemplo 1
h
x
Ï=a(x-h)™+k, a<0
Forma estándar de una función cuadrática
Sea f1x2 5 2x 2 $ 12x ! 23.
a) Exprese f en la forma estándar.
b) Bosqueje la gráfica de f.
En la sección 1.5 se explica cómo
completar el cuadrado.
Solución
a) Puesto que el coeficiente de x 2 no es 1, se debe factorizar este coeficiente a partir
de los términos relacionados con x antes de completar el cuadrado.
f 1x2 5 2x 2 $ 12x ! 23
5 21x 2 $ 6x 2 ! 23
f 1x 2 5 21x $ 3 2 2 ! 5
5 21x 2 $ 6x ! 92 ! 23 $ 2 # 9
Factorice 2 de los términos en x
Complete el cuadrado: sume 9 dentro
del paréntesis, reste 2 % 9 fuera
5 21x $ 32 2 ! 5
Factorice y simplifique
El vértice es 13, 52
La forma estándar es f 1x2 5 21x $ 3 2 2 ! 5.
SECCIÓN 2.5 Funciones cuadráticas; máximos y mínimos
195
b) La forma estándar indica que la gráfica de f se obtiene tomando la parábola
y 5 x 2, desplazándola 3 unidades a la derecha, alargándola por un factor de 2 y
moviéndola 5 unidades hacia arriba. El vértice de la parábola está en 13, 52 y la
parábola abre hacia arriba. La gráfica se bosqueja en la figura 1 después de notar que el intersecto y es f 102 5 23.
y
Ï=2(x-3)™+5
25
23
15
5
Vértice (3, 5)
0
Figura 1
x
3
■
Valores máximo y mínimo de
funciones cuadráticas
Si una función cuadrática tiene vértice 1h, k2 , entonces la función tiene un valor mínimo en el vértice si abre hacia arriba y un valor máximo en el vértice si abre hacia
abajo. Por ejemplo, la función graficada en la figura 1 tiene un valor mínimo 5 cuando x 5 3, puesto que el vértice 13, 52 es el punto mínimo sobre la gráfica.
Valor máximo o mínimo de una función cuadrática
Sea f una función cuadrática con forma estándar f 1x2 5 a1x " h 2 2 # k. El
valor máximo o mínimo de f ocurre en x 5 h.
Si a
0, entonces el valor mínimo de f es f1h2 5 k.
Si a ! 0, entonces el valor máximo de f es f 1h 2 5 k.
y
y
Máximo
k
k
0
Mínimo
h
Ï=a(x-h)™+k,
0
a>
0
x
h
Ï=a(x-h)™+k,
<
0
a
x
196
CAPÍTULO 2 Funciones
Ejemplo 2
Valor mínimo de una función cuadrática
Considere la función cuadrática f 1x2 5 5x 2
a) Exprese f en la forma estándar.
b) Bosqueje la gráfica de f.
c) Halle el valor mínimo de f.
y
Ï=5(x-3)™+4
49
Solución
a) Para expresar esta función cuadrática en la forma estándar, se completa el
cuadrado.
f 1x2 5 5x 2
30x ! 49
5 51x 2
6x 2 ! 49
5 51x
(3, 4)
4
0
Figura 2
30x ! 49.
3
Valor
mínimo 4
x
2
6x ! 92 ! 49
5#9
32 2 ! 4
5 51x
Factorice 5 de los términos en x
Complete el cuadrado: sume 9 dentro
del paréntesis, reste 5 " 9 fuera
Factorice y simplifique
b) La gráfica es una parábola que tiene su vértice en 13, 42 y abre hacia arriba,
como se bosqueja en la figura 2.
c) Puesto que el coeficiente de x 2 es positivo, f tiene un valor mínimo. El valor
mínimo es f132 5 4.
Ejemplo 3
■
Valor máximo de una función cuadrática
Considere la función cuadrática f1x2 5
a) Exprese f en la forma estándar.
x 2 ! x ! 2.
b) Bosqueje la gráfica de f.
c) Encuentre el valor máximo de f.
Solución
a) Para expresar esta función cuadrática en la forma estándar, se completa el
cuadrado.
y5
x2 ! x ! 2
5
1x 2
5
Ax
5
Ax
2
x2 ! 2
x!
1 2
2B
1
4B
Factorice -1 de los términos en x
1
!2
12 14
! 94
Complete el cuadrado: sume 41
dentro del paréntesis, reste
1 12 41 fuera
Factorice y simplifique
b) De la forma estándar se puede observar que la gráfica es una parábola que abre
hacia arriba y tiene vértice A 12, 94 B . Como ayuda para trazar la gráfica, se encuentran las intersecciones. La intersección y es f 102 5 2. Para hallar las intersecciones con x, se establece f 1x2 5 0 y se factoriza la ecuación resultante.
x2 ! x ! 2 5 0
1x 2
1x
x
22 5 0
22 1x ! 1 2 5 0
SECCIÓN 2.5 Funciones cuadráticas; máximos y mínimos
Así, las intersecciones x son x 5 2 y x 5
y
1
197
1. La gráfica de f se traza en la figura 3.
9
! 2, 4@
Valor máximo
9
4
1
_1
Figura 3
Gráfica de f 1x 2 5
0
1
2
x
x2 ! x ! 2
c) Puesto que el coeficiente de x 2 es negativo, f tiene un valor máximo, que es
f A 12 B 5 49.
■
Expresar una función cuadrática en la forma estándar ayuda a bosquejar su gráfica así como a hallar su valor máximo o mínimo. Si se está interesado sólo en hallar
el valor máximo o mínimo, entonces hay una fórmula para hacerlo. Esta fórmula se
obtiene completando el cuadrado para la función cuadrática general como sigue:
f 1x2 5 ax 2 ! bx ! c
5 aax2 !
b
xb ! c
a
Factorice a de los términos en x
Complete el cuadrado:
b2
b
5 aax ! x ! 2 b ! c
a
4a
2
5 aax !
b
b !c
2a
2
b2
aa 2b
4a
sume
reste
b2
dentro del paréntesis,
4a2
b2
a 2b
4a
fuera
2
b
4a
Factorice
Esta ecuación está en la forma estándar con h 5 b/12a2 y k 5 c b2/14a2 .
Puesto que el valor máximo o mínimo ocurre en x 5 h, se tiene el resultado siguiente.
Valor máximo o mínimo de una función cuadrática
El valor máximo o mínimo de una función cuadrática f 1x2 5 ax 2 ! bx ! c
ocurre en
b
x5
2a
Si a " 0, entonces el valor mínimo es f a
b
b.
2a
Si a # 0, entonces el valor máximo es f a
b
b.
2a
CAPÍTULO 2 Funciones
200
Los comandos maximum y minimum en una calculadora TI-82 o TI-83 proveen
otro método para hallar valores extremos de funciones. En el ejemplo siguiente se
usa este método.
Ejemplo 7
Un modelo para el índice de precios de alimentos
Un modelo para el índice de precios de alimentos (el precio de una “canasta” representativa de alimentos) entre 1990 y 2000 está dado por la función
I1t 2 5
0.0113t 3 ! 0.0681t 2 ! 0.198t ! 99.1
donde t se mide en años desde la mitad de 1990, así que 0 t 10, e I1t 2 se escala
de modo que I132 5 100. Estime el tiempo cuando la comida fue más cara durante
el periodo 1990-2000.
Solución La gráfica de I como una función de t se muestra en la figura 8(a). Al
parecer hay un máximo entre t 5 4 y t 5 7. Usando el comando maximum como se
muestra en la figura 8(b), se puede observar que el valor máximo de I es casi
100.38, y ocurre cuando t < 5.15, que corresponde a agosto de 1995.
102
102
Maximum
X=5.1514939
0
96
10
Y=100.38241
0
96
10
a)
b)
Figura 8
2.5
■
Ejercicios
1–4 ■ Se da la gráfica de una función cuadrática.
a) Determine las coordenadas del vértice.
b) Halle el valor máximo o mínimo de f.
1. f 1x 2 5
x 2 ! 6x
2. f 1x2 5
5
1 2
2x
3. f 1x 2 5 2x 2
2x ! 6
y
y
1
x
0
1
x
1
y
1
1
0
1
4. f 1x 2 5 3x 2 ! 6x
1
y
5
0
4x
1
x
0
1
x
202
CAPÍTULO 2 Funciones
y 5 0.005x 2 ! x ! 5, donde x es la distancia que la bola
ha viajado horizontalmente, y y es la altura sobre el nivel del
suelo, ambas medidas en pies.
a) ¿Cuál es la altura máxima que alcanza la bola?
b) ¿Qué tan lejos ha viajado horizontalmente la bola
cuando choca con el suelo?
¿Cuántos árboles se deben plantar por acre a fin de obtener
la producción máxima de manzanas?
66. Peces migratorios Un pez nada a una velocidad √ relativa al agua, contra una corriente de 5 millas/h. Con un modelo matemático de gasto de energía, se puede mostrar que la
energía total E requerida para nadar una distancia de 10 millas está dada por
E1√2 5 2.73√ 3
61. Ingreso Un fabricante encuentra que el ingreso generado
por vender x unidades de cierto artículo está dado por la
función R1x 2 5 80x 0.4x 2, donde el ingreso R1x 2
se mide en dólares. ¿Cuál es el ingreso máximo y cuántas
unidades se tienen que fabricar para obtener ese máximo?
62. Ventas Un vendedor de bebidas carbonatadas en una popular playa analiza sus registros de ventas, y encuentra que
si vende x latas de bebida en un día, su ganancia (en
dólares) está dada por
P1x 2 5
0.001x 2 ! 3x
10
√
5
Los biólogos creen que los peces migratorios tratan de
reducir al mínimo la energía total requerida para nadar una
distancia fija. Encuentre el valor de √ que minimiza la
energía requerida.
NOTA: este resultado ha sido comprobado; los peces migratorios nadan contra la corriente a una velocidad 50% mayor que
la velocidad de la corriente.
1800
¿Cuál es su ganancia máxima por día, y cuántas latas debe
vender para que la ganancia sea máxima?
63. Publicidad La efectividad de un comercial de televisión
depende de cuántas veces lo vea un televidente. Después de
algunos experimentos una agencia de publicidad encuentra
que si la efectividad E se mide en una escala de 0 a 10,
entonces,
E1n 2 5 32 n
1 2
90 n
donde n es el número de veces que un televidente ve un determinado comercial. Para que un comercial tenga efectividad máxima, ¿cuántas veces lo debe ver un televidente?
64. Productos farmacéuticos Cuando cierto fármaco se
toma oralmente, su concentración en el torrente sanguíneo
del paciente después de t minutos está dada por
C1t2 5 0.06t 0.0002t 2, donde 0 " t " 240 y la concentración se mide en mg/L. ¿Cuándo se alcanza la concentración máxima, y cuál es esa concentración máxima?
65. Agricultura El número de manzanas que produce cada
árbol en una huerta depende de la densidad de árboles plantados. Si se plantan n árboles en un acre de tierra, entonces
cada árbol produce 900 9n manzanas. Así que el número
de manzanas producidas por acre es
A1n 2 5 n1900
9n 2
67. Ingeniería de carreteras Un ingeniero desea calcular
el número máximo de automóviles que pueden viajar de
manera segura en una determinada carretera a una velocidad
especificada. Se supone que cada automóvil mide 17 pies de
longitud, viaja a una velocidad s y sigue al automóvil frente
a él a la “distancia segura” para esa velocidad. Encuentra
que el número N de automóviles que pueden pasar en determinado punto por minuto se modela mediante la función
N1s 2 5
88s
17 ! 17 a
s 2
b
20
¿A qué velocidad puede el mayor número de automóviles
viajar con seguridad por la carretera?
68. Volumen de agua Entre 0ºC y 30ºC, el volumen V (en
centímetros cúbicos) de 1 kg de agua a una temperatura T
está dado por la fórmula
V 5 999.87
0.06426T ! 0.0085043T 2
0.0000679T 3
Encuentre la temperatura a la cual el volumen de 1 kg de
agua es un mínimo.
SECCIÓN 2.6 Modelado con funciones
69. Tos Cuando un objeto extraño alojado en la tráquea fuerza
a una persona a toser, el diafragma empuja hacia arriba causando un incremento de presión en los pulmones. Al mismo
tiempo la tráquea se contrae, y provoca que el aire expelido
se mueva más rápido e incremente la presión sobre el objeto
extraño. De acuerdo con el modelo matemático de toser, la
velocidad √ de la corriente de aire por la tráquea de una persona de tamaño promedio se relaciona con el radio r de la
tráquea (en centímetros) mediante la función
√ 1r2 5 3.211
r2r 2,
1
2
!r!1
Determine el valor de r para el cual √ es un máximo.
71. Minimizar una distancia Cuando se busca un valor mínimo o máximo de una función, algunas veces se considera
más fácil trabajar con una función más simple.
a) Suponga que g1x 2 5 1f 1x2 , donde f 1x 2 # 0 para toda
x. Explique por qué los mínimos y máximos locales de
f y g ocurren en los mismos valores de x.
b) Sea g1x2 la distancia entre el punto 13, 0 2 y el punto
1x, x 2 2 sobre la gráfica de la parábola y 5 x 2. Exprese a
g como una función de x.
c) Encuentre el valor mínimo de la función g que encontró
en el inciso b). Use el principio descrito en el inciso a)
para simplificar su trabajo.
72. Máximo de un polinomio de cuarto grado Encuentre el
valor máximo de la función
Descubrimiento • Debate
70. Máximos y mínimos En el ejemplo 5 se analizó una
situación del mundo real en la que el valor máximo de una
función es importante. Mencione otras situaciones cotidianas en las que un valor máximo o mínimo es importante.
2.6
203
f 1x2 5 3 " 4x 2
x4
[Sugerencia: sea t 5 x 2.]
Modelado con funciones
Muchos de los procesos estudiados en las ciencias físicas y sociales requieren entender cómo varía una cantidad respecto a otra. Hallar una función que describe la dependencia de una cantidad en otra se llama modelado. Por ejemplo, un biólogo observa que el número de bacterias en cierto cultivo se incrementa con el tiempo. Él
intenta modelar este fenómeno mediante la determinación de la función precisa (o
regla) que relaciona la población de bacterias con el tiempo transcurrido.
En esta sección se aprenderá cómo hallar modelos que se pueden construir con
propiedades geométricas o algebraicas del objeto bajo estudio. (La determinación
de modelos a partir de datos se estudia en la parte Enfoque en el modelado al final de
este capítulo.) Una vez que se encuentra el modelo, se emplea para analizar y predecir propiedades del objeto o proceso bajo estudio.
Modelado con funciones
Empezaremos con una situación simple de la vida real que ilustra el proceso de modelado.
Ejemplo 1
Modelado del volumen de una caja
Una compañía productora de cereal fabrica cajas para empacar su producto. Por razones estéticas, la caja debe tener las siguientes proporciones: su amplitud es tres
veces su profundidad y su altura es cinco veces su profundidad.
a) Halle una función que modele el volumen de la caja en términos de su profundidad.
b) Encuentre el volumen de la caja si su profundidad es 1.5 pulgadas.
c) ¿Para qué profundidad el volumen es 90 pulg3?
d) ¿Para qué profundidad el volumen es mayor que 60 pulg3?