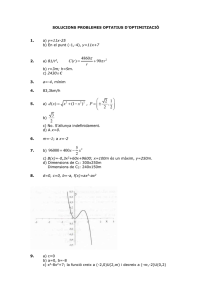
Una persona A se encuentra en la cumbre de un cerro de 250m de

Una persona A se encuentra en la cumbre de un cerro de 250m de
altura, situado cerca de la orilla del mar. Otra persona B se encuentra
en un barco. La persona A puede observar la orilla del mar con un
ángulo de depresión de 52º y la persona B puede observar la cumbre
de la montaña con un ángulo de elevación de 23º. Calcula: a) La
distancia a la que se encuentra el barco de la orilla del mar. b) La
distancia entre las dos personas
A
52°
250 m
y
x
tan (52°) = y/250m  y = 250m tan(52°) = 320 m
tan (23°) = 250m/(x+y)  x+y = 250m / tan(23°) = 589 m
x = 589 m – y = 589 m – 320m = 269 m
Distancia AB
Pitágoras: AB2 = 5892 + 2502 = 409421 m2
AB = √(409421 m2) = 640 m
(nota: redondeé todos los resultados a números enteros)
Respuestas:
a) distancia del barco a la orilla del mar: x = 269 m
b) distancia entre las dos personas: AB = 640 m
23°
B