bootstrap

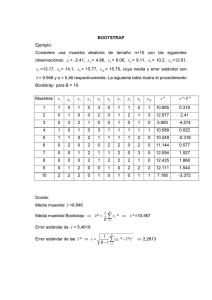
Introducción al Bootstrap y
sus aplicaciones
Las computadoras modernas han hecho posible ciertas formas de manipulación
y análisis de datos antes inconcebibles.
La visualización dinámica de datos, la simulación y los métodos de remuestreo
son algunos ejemplos de enfoques que, apoyados en las capacidades de los
ordenadores modernos, han enriquecido el trabajo de exploración y análisis
estadístico de datos. La relación entre ordenadores y análisis de datos es
patente para el caso de las llamadas técnicas de remuestreo de datos (‘data
resampling’), entre las que encontramos el Jacknife, los test de aleatorización y
permutación, la validación cruzada y el bootstrap.
El bootstrap permite resolver problemas relacionados con
Valorar el sesgo y el error muestral de un estadístico calculado a partir de una
muestra.
Establecer un intervalo de confianza para un parámetro estimado.
Realizar una prueba de hipótesis respecto a uno o mas parámetros
poblacionales.
Este enfoque puede resultar de interés para los investigadores, no solo
porque es menos restrictivo que el enfoque estadístico clásico, sino también
porque es más general en su formulación y más simple de comprender en lo
referente al procedimiento básico que subyace al método.
Consideraciones generales sobre la inferencia estadística clásica
Un objetivo común en la investigación es realizar inferencias probabilistas respecto
a algún aspecto de interés de la población objeto de estudio.
La estadística inferencial se ha ocupado de este problema estudiando cómo a partir
de la información limitada que facilita un estimador , obtenido en una muestra
aleatoria, podemos hacer afirmaciones, de tipo probabilístico, respecto al parámetro
desconocido, .
Una de las preocupaciones del analista será la exactitud (accuracy) con la que las
estimaciones captan al parámetro. La determinación de la exactitud de las
estimaciones descansa sobre el cálculo del error típico del estadístico (desviación
típica de su distribución muestral).
Esta forma de trabajo ha demostrado ser una excelente estrategia cuando las
asunciones impuestas son adecuadas al tipo de datos que se generan en la disciplina
en la que se va a emplear el modelo estadístico. Sin embargo, cuando los supuestos
en que estos métodos se basan no concuerdan con los datos los resultados obtenidos
con ellos son, lógicamente, menos de fiar.
Muchas veces se justifican la persistencia en la utilización de la distribución normal
en las ventajas computacionales que proporcionaba antes de la irrupción de los
ordenadores. Por otro lado, aun cuando las asunciones distribucionales sean
admisibles la obtención del error típico, en contra de lo que podría parecer, no es
posible para todos los estimadores.
Introducción Conceptual al Bootstrap
Frente al enfoque tradicional han sido desarrollados, o más bien puestos de
actualidad, una serie de métodos basados en cálculos intensivos por medio de
ordenadores destinados a obtener medidas de la precisión de las estimaciones
(errores típicos, sesgo, intervalos confidenciales).
El bootstrap introducido por Efron en 1979, se diferencia del enfoque
tradicional paramétrico en que emplea un gran número de cálculos repetitivos
para estimar la forma de la distribución muestral del estadístico, en lugar de
fuertes asunciones distribucionales y fórmulas analíticas.
Esto permite al investigador hacer inferencias en casos donde tales soluciones
analíticas son inviables, y donde tales asunciones son insostenibles. El
bootstrap no es, por tanto, un estadístico per se. Más bien, es una aproximación
al uso de la estadística para hacer inferencias sobre los parámetros
poblacionales.
El bootstrapping descansa en la analogía entre la muestra y la
población de la cual la muestra es extraída.
La idea central es que muchas veces puede ser mejor extraer conclusiones sobre
las características de la población estrictamente a partir de la muestra que se
maneja, que haciendo asunciones quizás poco realistas sobre la población.
El bootstrapping implica remuestreo (resampling) de los datos obtenidos en una
muestra, con reemplazamiento, muchas muchas veces para generar una
estimación empírica de la distribución muestral completa de un estadístico.
El bootstrap puede considerarse como un tipo especial de simulación
denominada simulación basada en los datos.
INFERENCIA ESTADISTICA MEDIANTE BOOTSTRAP
Las técnicas de simulación agrupadas bajo el nombre genérico de
bootstrap se ocupan de los mismos asuntos que la estadística
paramétrica pero bajo otro enfoque.
Las ideas básicas de la estadística no han cambiado lo que ha
cambiado es su implementación.
La irrupción de los ordenadores ha aportado rapidez y flexibilidad en
la aplicación de ciertas ideas hasta ahora aparcadas, permitiendo
analizar aspectos no abordables con facilidad analíticamente.
La idea básica del bootstrap es tratar la muestra como si fuera la
población, y aplicar el muestreo Monte Carlo para generar una
estimación empírica de la distribución muestral del estadístico.
La verdadera estimación Monte Carlo requiere un conocimiento total
de la población, pero por supuesto este no esta generalmente
disponible en la investigación aplicada. Típicamente, tenemos sólo una
muestra extraída de esa población, debido a lo cual es por lo que
necesitamos, antes de nada, inferir θ a partir de θ^.
El algoritmo bootstrap
En el bootstrapping, tratamos la muestra como si fuera la población y realizamos un
procedimiento del estilo Monte Carlo sobre la muestra. Esto se hace extrayendo un
gran número de "remuestras" de tamaño n de la muestra original aleatoriamente y
con reposición.
Más formalmente, los pasos básicos en la estimación bootstrap son:
1) Construir una distribución de probabilidad empírica, F^(x) a partir de la muestra
asignando una probabilidad de 1/n a cada punto, x1, x2, ..., xn. Esta es la función de
distribución empírica (FDE) de x, la cual es el estimador no-paramétrico de máxima
verosimilitud de la función de distribución de la población, F(X).
2) A partir de la FDE, F^(x), se extrae una muestra aleatoria simple de tamaño n
con reposición. Esta es una "remuestra", x*b.
3) Se calcula el estadístico de interés, θ^, a partir de esa remuestra, dando θ^*b.
4) Se repiten los pasos 2 y 3 B veces, donde B es un número grande. La magnitud
de B en la práctica depende de las pruebas que se van a aplicar a los datos. En
general, B debería ser de entre 50 a 200 para estimar el error típico de θ^, y al
menos de 1000 para estimar intervalos de confianza alrededor de θ^.
5) Construir una distribución de probabilidad a partir de los B θ^*b asignando una
probabilidad de 1/B a cada punto, θ^*1, θ^*2, ..., θ^*B. Esta distribución es la
estimación bootstrap de la distribución muestral de θ^, F^*(θ^*) . Esta distribución
puede usarse para hacer inferencias sobre θ.
La afirmación fundamental del bootstrapping es que una distribución de frecuencias
relativas de esos θ^* calculada a partir de las remuestras es una estimación de la
distribución muestral de θ^.
El estimador bootstrap del parámetro θ se define como:
En algunas ocasiones se tiene algún conocimiento más que el estrictamente aportado
por la muestra, por ejemplo se conoce la función de distribución de la variable objeto
de estudio pero se desconocen los parámetros, que deben ser estimados. En estos
casos se estimarían los parámetros a partir de la muestra y el remuestreo se realizaría
a partir de la función teórica conocida, con los parámetros estimados, en lugar de a
partir de la FDE construida a partir de la muestra. En este caso hablamos de Bootstrap
Paramétrico.
ESTIMACION BOOTSTRAP DEL ERROR TIPICO
El bootstrap y otras técnicas de remuestreo surgieron como métodos
basados en cálculos intensivos mediante ordenador que permiten ofrecer
medidas de la precisión de los estimadores estadísticos. Uno de esos
indicadores de precisión en las estimaciones es el Error Típico del
estimador.
Para algunos casos como el de la media aritmética existen fórmulas
sencillas que nos permiten estimar el valor del error típico.
Pero no siempre es este el caso, como ocurre con la mediana o con las
medias recortadas, por citar dos estadísticos relativamente simples. La
estimación bootstrap del error típico es posible para todos los estimadores
y no requiere cálculos teóricos.
El algoritmo bootstrap trabaja extrayendo muchas muestras bootstrap
independientes, calculando en cada una de ellas el correspondiente
estadístico, y estimando el error típico de θ^ mediante la desviación típica
de las replicaciones.
En cuanto al número de replicaciones necesarias para efectuar la
estimación del error típico suelen considerarse suficientes 100 remuestras,
variando el número indicado por los diferentes autores entre 50 y 200.
INTERVALOS CONFIDENCIALES
Otra forma de acercarse al problema de la precisión de las estimaciones
es a través de la construcción de intervalos de confianza. En el contexto
paramétrico clásico un intervalo confidencial tiene la siguiente estructura
general
P( θ^± Error Máximo) = 1 -α ,
donde 1 - α es el Nivel de confianza y
Error Máximo = valor absoluto de la Función de Distribución
correspondiente al percentil α /2 · Se
Una vez más, como se desprende de la expresión anterior, es necesario
conocer la distribución muestral del estadístico, tanto en lo que se refiere a
su forma como a su error típico.
Desde el enfoque del bootstrapping se han propuesto varios métodos de
construcción de intervalos confidenciales alternativos al enfoque clásico.
Por ejemplo hay varios métodos como: de aproximación normal, percentil,
percentil corregido, percentil corregido y acelerado, percentil t, etc.
Respecto al número de remuestras necesario para llevar a cabo la
construcción de intervalos confidenciales por este método (y en general por
los métodos bootstrap) se fija entre 1000 y 2000, para intentar garantizar
una mejor estimación de las colas de la distribución.
Bootstrap y la enseñanza de la estadística
Por otro lado, el procedimiento bootstrap resulta relativamente simple de
comprender, aspecto que se ha señalado como otra ventaja importante de las
técnicas de remuestreo, especialmente en el ámbito de la docencia.
Hay muchos autores, cuales han planteado que este enfoque puede resultar
beneficioso en el contexto de la enseñanza, ya que los estudiantes parecerían
comprender mejor ciertos conceptos si se utiliza esta perspectiva en lugar del
método clásico.
Esto se explicaría porque la descripción de los métodos no requiere
fundamentos ni expresiones matemáticos que pueden resultar complejos o
abstractos para muchos estudiantes, simplemente se necesita poder simular
un proceso de remuestreo de datos, lo que en la actualidad puede hacerse
fácilmente mediante un software apropiado.
En síntesis, podemos decir que el remuestreo proporciona una analogía más
concreta de los conceptos estadísticos y favorece un aprendizaje más activo,
ya que los estudiantes pueden controlar y experimentar por ellos mismos los
resultados de la simulación.
Por último, el bootstrap no es exigente en cuanto al cumplimiento de
supuestos teóricos para su aplicación y es, en este sentido, menos restrictivo
que las técnicas convencionales.
Se ha señalado que la validez del bootstrap se basa en un único supuesto o
principio que subyacente al procedimiento en sí mismo.
El **método bootstrap** aunque ya usado anteriormente, fue descrito de
forma sistemática por Efron en 1979.
El nombre alude al cordón de los zapatos, recordando la imagen de alguien
intentando salir del barro tirando del cordón de sus propios zapatos, y
consiste, si tenemos una muestra de tamaño N, en generar un gran número de
muestras de tamaño N efectuando un **muestreo con reemplazamiento** de
esos valores.
Puesto que el enfoque se apoya en la capacidad de la muestra para reflejar o
representar los aspectos relevantes de la población de la cual fue extraída, la
calidad de la muestra resulta crucial, sea porque no ha sido extraída por medio
de un procedimiento que asegure cierta representatividad o sea porque su
tamaño es demasiado pequeño.
En estas situaciones, puede ser dudoso que la información ofrecida por la
muestra permita estimar las propiedades desconocidas de la población.
No obstante, estas limitaciones son igualmente aplicables a las técnicas
clásicas, ya que también se basan en la idea de selección aleatoria y dependen
en su eficiencia del tamaño de la muestra.
Así, se ha afirmado que los métodos bootstrap permitirían ‘extraer lo
máximo a partir de la poca información disponible’.
Algunas barreras y limitaciones en el uso del bootstrap
Las razones en favor del bootstrap hacen suponer que se trataría de un
enfoque potencialmente útil para el análisis de datos, así como para la
enseñanza de la estadística en el área.
Sin embargo, esta metodología no ha sido incorporada en toda su extensión
al repertorio de herramientas que se aplican en las investigaciónes.
Una razón de este hecho sería el escaso conocimiento que los investigadores
tienen de las técnicas de remuestreo, puesto que a pesar de su relativa
simplicidad, no se incluyen como contenido en la formación de grado o
posgrado.
Otra barrera añadida pareciera ser que las técnicas bootstrap no estén
incorporadas de forma accesible a los programas estadísticos más populares,
como SPSS pero esta incluido en programas mas especializadas como
Resampling Stats, Stata, Statistica y SimStat, etc.
Por otro lado, algunos autores manifiestan que además de los factores
mencionados, existiría una dosis de ‘conservadurismo metodológico’ por el
cual los investigadores preferirían los métodos clásicos, aún incluso
existiendo evidencia en favor de la superioridad de las nuevas técnicas.
COMENTARIOS FINALES
El método bootstrap no pretende ser un sustituto de las técnicas estadísticas
tradicionales, de la misma manera que las pruebas no paramétricas clásicas
no pretenden ser sustitutas universales de las pruebas paramétricas.
Este nuevo tipo de técnicas están pensadas para situaciones en donde las
pruebas inferenciales al uso no tienen cabida, pues cuando las condiciones
de aplicación de estas son las correctas su funcionamiento supera al de las
posibles alternativas.
"La presunción del bootstrap es que la distribución muestral del estadístico
que se está estudiando y la distribución muestral encontrada mediante este
proceso iterativo son, para una amplia gama de estadísticos, esencialmente
idénticas"
Aun admitiendo este principio es conocido que una muestra, incluso
cuando se emplean técnicas adecuadas de muestreo, puede presentar ciertas
peculiaridades debido a las fluctuaciones muestrales. Si extraemos
múltiples muestras de una población esas peculiaridades se anulan (como
ocurre en la simulación Monte Carlo), pero en el bootstrap al remuestrear
constantemente a partir de la misma muestra original corremos el riesgo de
perpetuar esas peculiaridades y que la distribución muestral construida esté
distorsionada.
Como conclusión, el bootstrap es una técnica de remuestreo que puede
resultar de gran interés, tanto por sus capacidades como enfoque de análisis
de datos como por su potencial en el ámbito de la enseñanza.
Como herramienta de análisis estadístico, proporciona un enfoque general
que permite afrontar problemas diversos, sin la necesidad de asumir
supuestos teóricos que pueden resultar poco realistas, como supuestos
relativos a la distribución de los datos.
En su lugar, el bootstrap usa la información de la muestra para estimar,
mediante remuestreo de los propios datos, propiedades de los estimadores
estadísticos y así poder realizar tareas tales como crear un IC o realizar un
test de hipótesis.
Obviamente, la validez del enfoque depende fundamentalmente de la
calidad o capacidad de la muestra para contener o representar
apropiadamente las características de la población.
Por su sencillez y generalidad, el enfoque también resulta atractivo para ser
implementado en la docencia.
Este método parece más fácil de comprender que las técnicas de inferencia
clásica, ya que en lugar de explicaciones o formulaciones matemáticas que
pueden resultar abstractas para los estudiantes se utiliza una metodología
basada principalmente en realizar experiencias.
En lo fundamental, podemos decir que este enfoque solo requiere que el
estudiante sea capaz de comprender y aplicar nociones básicas de estadística
descriptiva, tales como distribuciones de frecuencias, histogramas,
varianzas y percentiles.
Métodos bootstrap avanzados
Aclaramos que esta introducción no ha contemplado algunos temas
importantes que deberían ser profundizados por los interesados.
Por ejemplo, existen formas alternativas de obtener IC que pueden ser más
eficientes en ciertos casos (como el método BCa).
Por otro lado, también debemos mencionar que cuando se trata de
estructuras de datos más complejas, como medidas correlacionadas o datos
basados en muestras estratificadas, puede ser necesario adaptar el
procedimiento bootstrap básico, ya que el muestreo con reposición debe
realizarse respetando otras exigencias de la información y del problema que
se está analizando.
Un ejemplo de este tipo, es el bootstrap de bloques móviles, más apropiado
cuando se trabaja con datos o modelos de series temporales.
Además, también existen algunas formas de modificación del esquema de
muestreo destinadas a mejorar la eficiencia del método es sus aspectos
computacionales, bootstrap equilibrado o ‘balanced bootstrap’ que fuerza a
que cada observación sea seleccionada un determinado número de veces en
todo el proceso bootstrap.
Todas estas cuestiones pueden revisarse y profundizarse consultando el
manual de Efron y Tibshirani (1993).
Referencias
Davison, A.C., y Hinkley, D.V. (1999). Bootstrap Methods and their
Applications. Cambridge, Inglaterra: Cambridge University Press.
Efron, B. (1979). Bootstrap methods: Another look at the jackknife. The
Annals of Statistics, 7, 1‐26.
Efron, B., y Tibshirani, R. (1993) An Introduction to the Bootstrap. Chapman
and Hall, New York, London.
Simon, J. (1997) Resampling: The New Statistics. Arlington, VA:
Resampling Stats, Inc. Disponible: www.resample.com
Simon, J. L., y Bruce, P. (1991) Resampling: A Tool for Everyday Statistical
Work, Chance, 4, 22–32.
Tierney, L. (1990). Lisp Stat An Object Oriented Environment for
Statistical Computing and Dynamic Graphics. NY: John Wiley & Sons.
Wood, M. (2005) The Role of Simulation Approaches in Statistics. Journal
of Statistics Education, 13, 3. Disponible:
www.amstat.org/publications/jse/v13n3/wood.html
Yu, Ch. H. (2003). Resampling methods: Concepts, Applications, and
Justification. Practical Assessment, Research & Evaluation, [Online] 8 (19).
Disponible: http://PAREonline.net/getvn.asp?v=8&n=19