prácticas de reconocimiento de formas

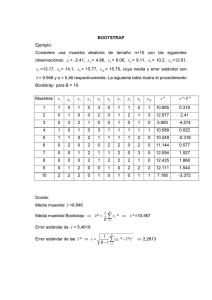
FACULTA DE INFORMÁTICA. INGENIERÍA INFORMÁTICA
PRÁCTICAS DE RECONOCIMIENTO DE FORMAS
PRÁCTICA 2. Bootstrap, NN, KNN y Test de Conjuntos de Datos.
TIEMPO: 4 horas
En Reconocimiento de Formas se denomina bootstrap a la técnica de generar aleatoriamente
conjuntos de datos de aprendizaje y test a partir de un conjunto de datos originales. El conjunto
de aprendizaje se utiliza para definir o entrenar un clasificador, mientras que el conjunto de test
se utiliza para ser clasificado en función del previo, obteniéndose la tasa de error.
Actividades Propuestas
1. Contruir una función MATLAB que realice el bootstrap:
[dataset1, dataset2] = Bootstrap(dataset,factor)
Donde factor es un número entre 0 y 1 que define la proporción entre dataset1 y dataset.
El conjunto dataset2 contiene todas las muestras u objetos no asignados a dataset1.
Para generar una separación de muestras lo más exacta posible debe asegurarse que la
frecuencia relativa de muestras de cada clase se mantiene lo más constante posible.
Sugerencias: Utilizar la función round() para calcular el número de muestras de cada clase
en el conjunto destino. Utilizar la función rand para generar números aleatorios. Al comienzo
de la función realizar una invocación de la forma: rand(‘state’, sum(100*clock)) para
generar una semilla aleatoria.
2. Construir una función de clasificación según el vecino más próximo en la forma:
[clase, objeto] = NN(dataset,vector)
Donde vector contiene las características de un objeto incógnita que debe ser clasificado en
función de dataset. Se proporciona como solución el número del objeto más cercano y la clase
de este objeto.
Sugerencia: Utilizar una función privada de distancia euclidea. La función min() proporciona
el mínimo y su posición.
3. Construir una función de clasificación según los k vecinos más próximos en la forma:
[clase, prob] = KNN(dataset,vector,k)
Donde prob es un vector de probabilidades de clasificar el objeto incógnita como cada una de
las clases, resultado que coincide con la distribución de muestras en los k vecinos más
próximos. El primer resultado corresponde a la clase más probable.
Sugerencia: Utilizar la función sort() que puede proporcionar también los índices de los
valores ordenados.
4. Construir una función de test de clasificación en la forma:
[error, prob] = Test_KNN(datset1,dataset2,k)
Donde dataset1 es el conjunto de entrenamiento y dataset2 es el conjunto de
comprobación. El resultado error es el porcentaje de muestras del conjunto de test que han
sido mal clasificadas. El resultado prob es una matriz cuadrada de dimensión igual al
número de clases; esta matriz contiene para cada clase el porcentaje de muestras de esa
clase que se clasifican como otra clase.
5. Contruir una función:
Resultado_KNN(dataset,factor,kmax)
Que representa gráficamente desde k=1 hasta k=kmax los errores vs k de la aplicación del
KNN al conjunto de datos especificado, utilizando el factor de bootstrap definido. Ejecutar
esta función para diferentes conjuntos de datos. Realizar una valoración sobre la
separabilidad de las distintas clases.
Sugerencia: Utilizar plot(vec_k, vec_error, marca), con una marca tipo como ‘ro-‘
o similar.