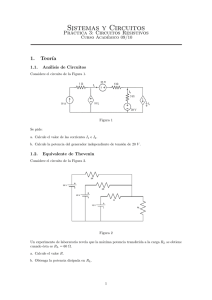
Introducción a la Teoría de Circuitos

Introducción a la teorı́a de circuitos
Parte 1
Circuitos de corriente continua
Ricardo Juan Palma Durán
Copyright (c) 2008 Ricardo Palma. Se otorga permiso para copiar, distribuir y/o modificar
este documento bajo los términos de la Licencia de Documentación Libre de GNU, Versión
1.2 o cualquier otra versión posterior publicada por la Free Software Foundation; sin Secciones
Invariantes ni Textos de Cubierta Delantera ni Textos de Cubierta Trasera. Una copia de la
licencia puede ser obtenida desde la web de la GNU Free Documentation License,
http://www.gnu.org/copyleft/fdl.html.
ii
Índice general
Introducción
V
1. Conceptos fundamentales
1.1. Corriente continua . . .
1.2. Tensión . . . . . . . . .
1.3. Corriente . . . . . . . . .
1.4. Potencia . . . . . . . . .
1.5. Ley de Ohm . . . . . . .
.
.
.
.
.
1
1
1
3
3
7
.
.
.
.
.
.
9
9
11
13
15
18
19
2. Elementos fundamentales
2.1. Resistencia . . . . . . . .
2.2. Bobina . . . . . . . . . .
2.3. Condensador . . . . . .
2.4. Fuente de tensión . . . .
2.5. Fuente de corriente . . .
2.6. Principio de conservación
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
de la energı́a
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3. Leyes de Kirchhoff
21
3.1. Conceptos previos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3.2. Ley de los nudos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.3. Ley de las mallas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
4. Asociaciones de elementos
4.1. Concepto de asociación de elementos
4.2. Asociaciones en serie . . . . . . . . .
4.2.1. Resistencias . . . . . . . . . .
4.2.2. Bobinas . . . . . . . . . . . .
4.2.3. Condensadores . . . . . . . .
4.2.4. Fuentes de tensión . . . . . .
4.2.5. Fuentes de corriente . . . . .
4.3. Asociaciones en paralelo . . . . . . .
4.3.1. Resistencias . . . . . . . . . .
4.3.2. Bobinas . . . . . . . . . . . .
4.3.3. Condensadores . . . . . . . .
4.3.4. Fuentes de tensión . . . . . .
4.3.5. Fuentes de corriente . . . . .
4.4. Más acerca de asociaciones . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
iii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
31
31
34
35
37
39
40
44
45
46
48
51
53
54
57
ÍNDICE GENERAL
iv
5. Resolución de circuitos en DC
5.1. Pistas para la resolución de circuitos . . . . . . . . .
5.2. Método de los nudos . . . . . . . . . . . . . . . . . .
5.2.1. Método de los nudos, ejercicios . . . . . . . .
5.3. Método de las mallas . . . . . . . . . . . . . . . . . .
5.3.1. Método de las mallas con fuentes de corriente
5.3.2. Método de las mallas, ejercicios . . . . . . . .
6. Terminologı́a, simbologı́a
6.1. Terminologı́a . . . . .
6.2. Simbologı́a . . . . . . .
6.3. Divisor de tensión . . .
y divisor
. . . . . .
. . . . . .
. . . . . .
7. Teoremas
7.1. Principio de superposición
7.2. Teorema de Thévenin . . .
7.3. Teorema de Norton . . . .
7.4. Relación Thevènin-Norton
7.5. Teoremas, ejercicios . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
de
. .
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
61
61
62
62
94
98
101
tensión
119
. . . . . . . . . . . . . . . . . . . . . . . . 119
. . . . . . . . . . . . . . . . . . . . . . . . 121
. . . . . . . . . . . . . . . . . . . . . . . . 124
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
127
. 127
. 136
. 141
. 143
. 146
Introducción
El origen de esta colección se remonta al verano del 2004, cuando unos amigos que, como
yo, estudiaban (y todavı́a estudian) Ingenierı́a Informática en la Escuela Técnica Superior de
Ingenierı́a Informática y Telecomunicaciones (ETSIIT) de la Universidad de Granada (UGR),
se vieron obligados a estudiar la asignatura de Fundamentos Fı́sicos de la Informática (FFI)
para la convocatoria de setiembre. Para ser sincero, no sé en qué momento se me pasó por la
cabeza decidir ayudarlos, pero ası́ fue.
Al igual que muchos de mis compañeros, algunos de los cuales todavı́a la tienen pendiente,
sufrı́ bastante para aprobar la asignatura de FFI. Cuando la aprobé, sin embargo, lo hice con
bastante buena nota, y siendo consciente de que, a diferencia de muchas otras asignaturas que
se han perdido en el baúl de los recuerdos, a ésta la dominaba. Ası́ pues, llegado el verano de
2004, decidı́ ayudar a estos amigos. Dado que por motivos de transporte quedar con ellos era
algo complicado, decidı́ tomar otra opción más complicada aún: hacerles unos apuntes para que
ası́ ellos autoaprendieran todo lo necesario para aprobar la asignatura.
Fue ası́ que decidı́ hacer los apuntes. He de reconocer que, si bien supusieron muchas horas de
trabajo, la idea de ayudar a mis amigos me mantuvo firme, ası́ que, a pesar de pasar un verano
un tanto peculiar, al final los acabé. Una vez aprobaron mis amigos, me pregunté qué harı́a
con los casi 500 folios de apuntes que habı́a escrito. Fue entonces cuando pensé que quizás los
apuntes podrı́an ser útiles a generaciones venideras. Cuando uno estudiaba FFI, era frustrante
ver que, ni contaba con buenos apuntes, ni contaba con buenos ejemplos para poner en práctica
los conocimientos teóricos. Ası́ pues, me decanté por la opción de escanearlos 1 , encuadernarlos
y subirlos a la página http://www.hijosdeeva.net, y he ahı́ que nacieron los famosos apuntes
de Ricardo Palma 2 .
En el momento en el que hice públicos los apuntes, varios amigos sugirieron la idea de que
intentara sacar algún beneficio por ello. No sé cómo habrı́a salido la idea, pero lo que sı́ es cierto
es que al final no me he arrepentido de distribuirlos libremente. Quizás la parte más satisfactoria
de todas es la de recibir correos de gente de diversas regiones de España, e incluso América del
Sur, agradeciéndote el trabajo. Momentos como esos hacen que te sientas realmente bien. A
ellos, gracias.
Pasaron los años, y la voz de otro amigo de la facultad no dejaba de sonar dentro de mi
cabeza: ¿por qué no pasas los apuntes a ordenador? Aunque tener unos apuntes que sabı́a que
tanta gente usaba era algo muy satisfactorio, el formato en el que se presentaban distaba de ser
bueno. Ciertamente, era bastante cutre, ası́ que, ya hará un año, decidı́ hacer caso de mi amigo
y comencé a pasar los apuntes a ordenador. En un principio opté por escribir los apuntes en
la famosa suite ofimática OpenOffice3 , la cual inicialmente me proporcionó resultados bastante
aceptables. Por desgracia, mantener un archivo con tantas imágenes insertadas, y en un formato
1
El escaneo fue posible gracias a un super escáner del que disponı́a el departamento de Electrónica y Tecnologı́a de los Computadores, y gracias, sobre todo, al que fue mi profesor en FFI, que me dejó usar la susodicha
máquina.
2
La primera vez que oı́ esa frase fue dos cursos más tarde, cuando un amigo me presentó a un amigo suyo
que, literalmente, me dijo ehh, ¿¡tú eres el de los famosos apuntes!?. Disculpad el pegote.
3
http://www.openoffice.org/ .
v
INTRODUCCIÓN
vi
no reconocido directamente por OpenOffice (el formato PostScript), hicieron del archivo del
manual de corriente continua una bestia incontrolable que conseguı́a, en incontables ocasiones,
sacarme de mis casillas. Apunto de acabar la primera parte de esta colección, decidı́ probar
LATEX4 , del cual no habı́an dejado de hablarme a lo largo de la carrera. Con LATEX, no sólo
obtuve unos resultados bastante mejores que con OpenOffice, sino que, además, los archivos que
conformaban el documento eran simples ficheros de texto plano que apenas requerı́an recursos
para ser procesados. En resumen, más rápido y mejor. Ası́ pues, tuve que repasar los apuntes
que tenı́a escritos en OpenOffice a LATEX (cuando comencé a usar LATEX tenı́a casi finalizado el
libro de corriente continua), lo cual hizo que este libro se retrasase en su salida más de un mes.
Esta colección es una introducción a la teorı́a de circuitos. Si bien el temario de la asignatura
de FFI era bastante más amplio, el núcleo de la asignatura trataba de teorı́a de circuitos básica,
y de ahı́ que me centrara en ello. Este libro, concretamente, comienza las andanzas por el mundo
de la teorı́a de circuitos, e introduce al lector al análisis de circuitos en condiciones de corriente
continua. Los circuitos de corriente continua son la base de la teorı́a de circuitos, ya que las
leyes y métodos empleados al trabajar con ellos mantienen su validez en circuitos de mayor
complejidad. Éste, por tanto, es el primer paso en nuestra carrera hacia el aprobado. Suerte.
Notas de la edición
Antes de que el lector pusiera el ojo en el contenido de este libro, me gustarı́a incitarle a que
me informara de cualquier errata que en él hallase: faltas de ortografı́a, errores matemáticos, o
simplemente burradas de las que no me haya dado cuenta... todo vale. A ser posible, que estas
sugerencias se envı́en por correo electrónico a la dirección [email protected].
No hace falta decir que, cualquier otro tipo de sugerencia, será gratamente recibida.
He de dejar constancia del hecho de que este libro se ha escrito un tanto deprisa y corriendo,
de modo que soy consciente de que en él ha de haber bastantes erratas fruto de la trascripción
hecha a partir de los apuntes escritos a mano. De nuevo ruego al lector de que me informe de
cualquier tipo de error, para poder mejorar el contenido del libro (a ser posible, en tiempo real).
4
Para quien no lo sepa, LaTeX es un sistema de escritura de documentos que discrepta de los editores
normales tipo OpenOffice o Microsoft Office. Éstos editores se conocen como editores WYSIWYG, es decir,
editores en los que lo que ves es lo que obtienes. Con LATEX, a diferencia, los documentos se escriben como
archivos de texto plano que son compilados, obteniendo unos resultados absolutamente profesionales.
Capı́tulo 1
Conceptos fundamentales
En este capı́tulo se definen varios conceptos que serán fundamentales a lo largo de todo
nuestro trabajo. Son los conceptos de corriente continua, tensión, corriente, potencia y Ley de
Ohm.
1.1.
Corriente continua
Se dice que un circuito es de corriente continua si todas las tensiones y corrientes que en él
hay son constantes en el tiempo.
Éste va a ser el tipo de circuito más sencillo que se resolverá en estos libros, pero, a su
vez, el más importante, ya que el análisis de otros circuitos más complejos (con dispositivos
electrónicos, con señales variables en el tiempo, . . . ) usará una metodologı́a muy similar, si no
idéntica, a la que ahora nos disponemos a emplear (fundamentalmente las Leyes de Kirchoff).
El término corriente continua suele abreviarse mediante sus siglas inglesas, a saber, DC 1.
1.2.
Tensión
El concepto de tensión o diferencia de potencial (ddp) nos deberı́a resultar familiar, ya que
se estudia en la primera parte de la asignatura de Fundamentos Fı́sicos de la Informática, que
es la asignatura a la que está dirigida este libro. No pretendemos hacer hincapié en el concepto
de tensión tal y como ya se habrá hecho, sino destacar dos propiedades muy importantes y que
cobran especial relevancia en el análisis de circuitos.
Por un lado, una tensión no es más que una diferencia del potencial eléctrico presente en dos
puntos. Por ejemplo, si en un punto A hay un potencial Va , y en un punto B hay un potencial
Vb , entonces entre A y B se dice que hay una tensión de:
Vab = Va − Vb
(1.1)
Desde el comienzo de este libro me gustarı́a remarcar algo referente a la fórmula (1.1). La
fórmula (1.1) dice que uve sub a,b es igual a uve sub a menos uve sub b. Es importante decir
esto, ya que mucha gente suele confundirse con el orden en el que se escriben los factores que
intervienen en la diferencia. Si estamos hallando V sub algo, otro algo, entonces en la diferencia
aparece primero V sub algo y después V sub otro algo.
Surge aquı́ un problema que el lector habrá tratado anteriormente, y es la imposibilidad
de conocer el potencial eléctrico en un punto determinado. Si bien en la fórmula anterior se
ha escrito con cierta despreocupación tanto Va como Vb , no es posible conocer ninguno
1
Del inglés direct current.
1
2
CAPÍTULO 1. CONCEPTOS FUNDAMENTALES
Figura 1.1: tomas de tierra
de esos valores. El lector sabrá que, en la realidad, sólo se puede conocer una diferencia de
potencial entre dos puntos, pero nunca el potencial en alguno de ellos por separado. Entonces,
parece que la fórmula arriba expuesta no tiene sentido, ya que ni Va ni Vb pueden conocerse.
Ahora bien, debemos rememorar también que, si bien eso es cierto, también es cierto que,
por convenio (es decir, porque-nos-sale-de-las-pelotas), y para facilitarnos las cosas, era común
fijar un punto del espacio arbitrario con potencial 0. Insistimos, eso es un convenio, ya que no se
puede conocer el potencial en un punto del espacio. Establecido ese punto de potencial 0, resulta
que las fórmulas matemáticas comienzan a cobrar algo más de sentido, de modo que ahora sı́ es
posible conocer los valores de potencial en cualquier punto del espacio. Debemos tener en cuenta
que lo que realmente importa, lo que realmente existe, son diferencias de potencial. Por tanto,
la elección de ese punto de potencial 0 no debe repercutir (y de hecho no repercute) en las
diferencias de potencial entre cualesquiera puntos del espacio.
A modo de ejemplo, supongamos que tenemos una pila normal de 1,5 voltios. Lo que viene
a significar que una pila sea de 1,5 voltios es que la tensión o diferencia de potencial que hay
entre su polo positivo y su polo negativo es de 1,5 voltios. Eso, simplemente eso y nada más,
es decir:
V+ − V− = 1,5V
Dependiendo de el punto que se fijase con potencial 0, se podrı́a llegar a conclusiones tan
dispares como que V+ = 17V y que V− = 1V , o que V+ = 1V y que V− = −0,5V , o que
V+ = 1,5V y que V− = 0V (en este último caso el punto de potencial 0 coincide con el polo
negativo de la pila). Ahora bien, en todos esos casos, es fácil ver que la diferencia sigue siendo
constante, e igual a 1,5V . Como se habı́a dicho, si bien los valores de potencial de un punto
pueden variar dependiendo del punto que se fije como punto de potencial 0, las diferencias
de potencial no cambian.
En el caso particular de los circuitos, ese punto de potencial 0 se denomina toma de tierra, o
simplemente, tierra. Hay diversos sı́mbolos usados para representar la toma de tierra, de entre
los cuales destacamos dos, representados en la Figura 1.1.
La toma de la izquierda es el sı́mbolo más común, y el que nosotros usaremos mayoritariamente a lo largo del libro.
Hay que destacar también que al potencial eléctrico en un punto del espacio también se
le conoce como tensión, sı́, como tensión. Esta nomenclatura puede dar lugar a confusiones.
Anteriormente, nosotros habı́amos definido tensión como una diferencia de potencial. Ahora
estamos diciendo que esos potenciales también son conocidos como tensión. Para ser sincero,
el término potencial no se usa demasiado. Digamos que, en teorı́a de circuitos, no se utiliza
a penas. En cambio, cuando no hay posibilidad de ambigüedad, el término tensión se refiere
al potencial en un punto (lo cual sólo tiene sentido, como hemos dicho antes, si hay toma de
tierra establecida). La conclusión entonces es que, dependiendo del contexto, la palabra tensión
puede referirse a una diferencia de potencial entre dos puntos, o bien al potencial en alguno de
esos puntos. En este contexto, muchas personas se refieren a la diferencia de potencial como
diferencia de tensión. De este modo ya no habrı́a posibilidad de confusión, ya que diferencia
de tensión harı́a referencia a la magnitud que es diferencia de potenciales, y tensión harı́a
referencia a cada uno de los respectivos potenciales. Es responsabilidad del que habla no dar
lugar a ambigüedades.
La otra propiedad que querı́amos señalar de la tensión o diferencia de potencial es que,
3
1.3. CORRIENTE
cuando una carga q se desplaza a través de una diferencia de potencial ∆V = Vf inal − Vinicial
entonces su energı́a potencial eléctrica varı́a tanto como:
∆U = q∆V
Ahora bien, si esa cantidad de carga es infinitamente pequeña, es decir, es un diferencial de
carga dq, entonces la variación de energı́a ∆U también se hace infinitamente pequeña, pasando
a ser dU, de modo que la fórmula anterior queda como:
dU = dq∆V
(1.2)
Expresión que usaremos para obtener la fórmula de la potencia en muy variadas situaciones.
1.3.
Corriente
Se define la corriente eléctrica como la cantidad de carga que atraviesa una determinada
superficie por unidad de tiempo, es decir:
I=
dq
dt
La corriente eléctrica se mide en Amperios (A). Un Amperio equivale a un Culombio por
segundo (C/s).
Hay que destacar que, en pocas palabras, una corriente eléctrica no es más que un flujo
de cargas, ya sean positivas o negativas, que se mueven por el espacio. Siendo estrictos, si
tomamos un objeto cargado positivamente, por ejemplo un bistec al que se le han inyectado
cargas positivas, y lo lanzamos por el aire, eso, ese bistec junto con sus cargas vendrı́a a formar
una corriente eléctrica. Dejando las discusiones cárnicas para otro momento, es necesario que el
lector se dé cuenta de que, si bien una corriente está formada por cargas positivas o negativas,
una corriente formada por cargas positivas no significa lo mismo que una corriente formada por
cargas negativas.
Por convenio (nuevamente), se establece una corriente eléctrica tiene el sentido de movimiento de las cargas positivas y opuesto al de las cargas negativas. De este modo, un flujo de cargas
positivas que se mueve de A a B representa una corriente eléctrica de A a B, pero si dichas
cargas fuesen negativas, representarı́a una corriente que se mueve de B a A. La Figura 1.2 lo
representa gráficamente.
1.4.
Potencia
La potencia de un sistema fı́sico puede definirse como la rapidez con la que varı́a su energı́a
por unidad de tiempo (dicho de otro modo, la cantidad de energı́a que gana o pierde por unidad
de tiempo). Entonces es evidente que su expresión matemática es:
P (t) =
dU
dt
Donde la potencia es una magnitud que se mide en Vatios (W ). Un Vatio equivale a un Julio
por segundo (J/s).
Si la potencia es positiva, P > 0, el sistema gana energı́a, que absorbe; en los sencillos
elementos que estudiaremos, esa energı́a, o bien podrá ser devuelta al resto del circuito, o bien
se disipará en forma de calor. En cualquier caso, la idea clave es que, si P > 0, el sistema
está absorbiendo energı́a, que por tanto se considera que consume de otro lugar.
4
CAPÍTULO 1. CONCEPTOS FUNDAMENTALES
Figura 1.2: corriente creada por cargas positivas y negativas
Si la potencia es negativa, P < 0, el sistema pierde energı́a, que devuelve a otro lugar;
en nuestros circuitos, ese fenómeno se traduce en que un elemento devuelve energı́a a otros
elementos, que podrán utilizar.
En el análisis de circuitos la variaciones de energı́a se deben al desplazamiento de cargas
a través de diferencias de potencial (tensiones), por tanto, usando la fórmula (1.2), se deduce
que:
dU
dq
P (t) =
= ∆V (t) = I(t)∆V (t)
dt
dt
Se concluye pues que la potencia generada o consumida de por una corriente I(t) que atraviesa
una diferencia de potencial ∆V (t) no es más que el producto de dicha corriente por dicha
diferencia de potencial.
Es de vital importancia preservar el criterio de signos, teniendo en cuenta que ∆V (t) es la
diferencia de potencial que se mide en el sentido de circulación de I(t), es decir, si I(t) se mueve
de un punto A a un punto B, la diferencia de potencialque requerimos para hallar P (t) es:
∆V (t) = VAB (t) = VA (t) − VB (t)
Esto quizás parezca una idiotez, y es por ello que vamos a insistir un poco más.
Ejercicio 1.1: Suponiendo que una corriente I = 1mA se mueve como indica la Figura 1.3
(de A hacia B), y que además VA = 5V y que VB = 10V , se pide hallar la potencia generada o
consumida por dicha corriente.
Figura 1.3: Ejemplo 1.1
Solución
P = I∆V y ∆V es la diferencia de potencial, o tensión, VAB = 5 − 10 = −5V , por tanto,
la potencia es:
P = 1 · 10−3 (−5V ) = −5 · 10−3 W
5
1.4. POTENCIA
Es decir, como P < 0, el sistema pierde energı́a. Recuérdese que la unidad del Vatio (W ),
representa la rapidez con que varı́a la energı́a del sistema; concretamente se mide en Julios (J )
por segundo, es decir, en este caso la potencia es de −5mJ/s, lo que significa que el sistema
pierde 5 julios de energı́a cada segundo.
Ejercicio 1.2: Se pide resolver el ejercicio anterior, pero tomando Va = 10V y Vb = 5V .
Solución
P = I∆V y ∆V es la diferencia de potencial, o tensión, VAB = 10 − 5 = 5V , por tanto, la
potencia es:
P = 1 · 10−3 (5V ) = 5 · 10−3 W
Obteniéndose un resultado opuesto al anterior, es decir, en este caso P > 0, por tanto el sistema
gana energı́a y a una razón de 5 julios por segundo.
Viene ahora un pequeño problema, que no es culpa mı́a, sino de la falta de criterio común
entre aquellos que decidieron inventar todo esto de los circuitos. Tampoco es algo grave, pero
a más de uno le puede proporcionar un dolor de cabeza si no se da cuenta de ello.
El problema viene en la definición que hemos dado de potencia:
P (t) = I(t)∆V (t)
En primer lugar, hay que destacar que en vez de escribir ∆V (t) escribiremos V (t), obviando el
hecho de que se trata de una diferencia de potencial.
A parte de ello, que no tiene la menor importancia, el problema radica en que en otros
textos esa diferencia de potencial ∆V (t) o V (t) (P (t) = I(t)V (t)) no es exactamente la misma
que nosotros hemos tomado, sino justo la contraria; es decir, con este criterio, si la corriente
I(t) circula de A hacia B, entonces ∆V (t) o V (t) es:
P (t) = VBA (t) = VB (t) − VA (t)
que es, como hemos dicho, la contraria a la que nosotros tomábamos. O lo que es lo mismo, es
la misma, pero cambiada de signo.
Evidentemente, si hacemos este cambio, el criterio de signos antes usado para determinar
si una potencia era consumida o generada es invertido. Las potencias que antes eran positivas,
ahora serán negativas, y las que antes eran negativas, ahora serán positivas. Por tanto, para
seguir distinguiendo entre lo que es potencia consumida o generada hay que, como hemos dicho,
invertir el criterio: ahora las potencias positiva representan potencia generada (la energı́a sale
del sistema), y la potencia negativa es potencia consumida (la energı́a entra al sistema).
El lector deberı́a ser capaz de ver que el criterio de signos es un mero convenio sin importancia, ya que al fin y al cabo lo que nos interesa es determinar si una potencia es generada o
consumida.
Por ejemplo, supongamos la corriente de la Figura 1.4. Si usamos el primer criterio de signos
que hemos explicado para hallar la potencia del sistema, tendremos que usar esta expresión:
P = IVAB = I(VA − VB ) = 5 · 10−3 (3 − 1) = 10 · 10−3 W
En este caso, como nos basamos en el primer criterio, al ser P > 0, se tratarı́a de potencia
6
CAPÍTULO 1. CONCEPTOS FUNDAMENTALES
Figura 1.4: una corriente cualquiera
consumida, es decir, el sistema gana energı́a.
Si por contra usamos el segundo criterio de signos, deberı́amos emplear esta expresión:
P = IVBA = I(VB − VA ) = 5 · 10−3 (1 − 3) = −10 · 10−3 W
Ahora bien, aunque la potencia ahora tenga signo negativo, al tratarse del segundo criterio de
signos, ésta se tratará de energı́a también consumida, es decir, que entra en el sistema.
Vemos por tanto que el criterio usado no importa, pues lo realmente útil es determinar, en
base a cualquiera de los dos criterios, si la energı́a es absorbida por el sistema o generada por
él.
Para concluir la charla acerca del criterio de signos, nosotros, a lo largo de este
texto, vamos a utilizar el criterio de signos que establece:
P (t) = IdeAaB (t)VAB (t)
(1.3)
Con lo cual, si P < 0 la potencia será generada (el sistema pierde energı́a), y si P > 0
la potencia será consumida (el sistema gana energı́a). Elegimos este criterio porque es
más intuitivo (va acorde con la idea clásica de potencia) y además no genera problemas de
signos a la hora de tratar las fórmulas de potencias y energı́as.
La variación de energı́a de un determinado sistema está ı́ntimamente relacionada con la
potencia. De hecho, de la definición:
dU
P (t) =
dt
Se puede despejar la variación de energı́a entre dos instantes t0 y t1 (es decir, podemos despejar
∆U = U(t1 ) − U(t0 )). De este modo se puede obtener cuánta energı́a gana o pierde un sistema
en un intervalo de tiempo. En nuestro caso concreto, hablamos de la energı́a ganada o perdida
debido al paso de una corriente eléctrica por una diferencia de potencial.
Para ello basta integrar la expresión anterior:
Z t1
Z t1
P (t)dt =
I(t)V (t)dt
(1.4)
∆U = U(t1 ) − U(t0 ) =
t0
t0
En corriente continua las corrientes y tensiones son constantes en el tiempo. Por tanto, la
potencia consumida o generada como consecuencia del movimiento de una corriente a través
de una tensión o diferencia de potencial, también será constante, de modo que la integral de la
expresión (1.4) se simplifica, obteniendo:
Z t1
dt = IV (t1 − t0 )
(1.5)
∆U = P
t0
La expresión (1.4) se usa en circuitos en los que las corrientes y tensiones varı́an en el tiempo. En
ese caso, si queremos obtener la energı́a consumida por cierta corriente I(t) habrá que hallar la
integral que dicha fórmula expresa, lo cual se deberı́a reducir a la clásica fórmula de la integral
por partes. Más adelante se harán ejemplos al respecto.
La fórmula (1.5) representa la fórmula de la energı́a consumida o generada si las corrientes
y tensiones del circuito son constantes en el tiempo, que es justamente lo que ocurre en los
circuitos de corriente continua. En ese caso, la expresión de la energı́a se simplifica bastante: no
hay que resolver ninguna integral, y se reduce a calcular el producto de la corriente en cuestión
por la tensión que atraviesa y por la duración del intervalo de tiempo.
7
1.5. LEY DE OHM
a
R
b
Figura 1.5: una resistencia
a
R
b
I
Figura 1.6: resistencia por la que circula una corriente de valor I
1.5.
Ley de Ohm
¿Qué es la Ley de Ohm? La ley de Ohm es la ley más básica dentro de la teorı́a de circuitos.
Forma el pan nuestro de cada dı́a, y no habrá circuito en el que no deba tenerse en cuenta.
La ley en cuestión dice:
Supongamos que a un material conductor se le aplica una diferencia de potencial
(tensión), V , entre sus extremos. Entonces, se cumple que a través de él circula una
corriente I proporcional a la tensión aplicada, siguiendo la fórmula:
I=
V
R
Donde R es una constante propia de cada material conductor, conocida como resistencia.
La resistencia de un material se mide en Ohmios (Ω).
Habı́amos establecido por convenio que la corriente tiene un sentido de movimiento igual
al de las cargas que la componen, en caso de ser positivas, y opuesto, en caso de ser negativas.
Supongamos ahora que tenemos un material conductor de resistencia R, tal y como muestra la
Figura 1.5.
Supongamos ahora que aplicamos a esta resistencia una tensión Vab tal que Va > Vb . La
cuestión es, ¿hacia dónde se dirige la corriente? Pensemos un poco al respecto. Si la corriente
estuviera formada por electrones (que tienen carga negativa), podemos deducir cuál es el sentido
de movimiento de los electrones en ese material resistivo. Concretamente, sabemos que los
electrones, y cualquier partı́cula en general, tiende a tener el mı́nimo de energı́a posible. En ese
sentido son como nosotros. Pues bien, como los electrones son cargas negativas, estos pierden
energı́a conforme se mueven hacia potenciales mayores. Por tanto, si Va > Vb , entonces los
electrones se moverán hacia el punto a por estar éste a mayor potencial, buscando ası́ tener
la menor energı́a posible. ¿Qué ocurre entonces? Pues que, dado que los electrones se mueven
hacia la izquierda (de b a a), y la corriente eléctrica tiene un sentido opuesto al del movimiento
de las cargas negativas, la corriente que se genera va de a a b, tal y como indica la Figura 1.6.
Si las cargas hubieran sido positivas, éstas habrı́an ido hacia el punto b, ya que las cargas
positivas pierden energı́a cuando se mueven a potenciales menores. Ası́, la corriente eléctrica
generada también habrı́a circulado de a a b, ya que las corrientes eléctricas tienen el sentido de
movimiento de las cargas positivas.
En cualquier caso, el valor de la corriente I habrı́a sido el dado por la Ley de Ohm:
I=
Vab
Va − Vb
=
R
R
En la práctica, la Ley de Ohm se aplica considerando el sentido de la corriente que
atraviesa la resistencia, de modo que, si la corriente se mueve del punto A al punto
8
CAPÍTULO 1. CONCEPTOS FUNDAMENTALES
B, su valor está dado por la expresión:
Iab =
Va − Vb
Vab
=
R
R
Donde es muy importante remarcar que la tensión medida es Vab , y no Vba , ya que la
corriente se está moviendo de A a B. Si la corriente se moviera de B a A, entonces
esa tensión sı́ serı́a Vba .
Referente a la Ley de Ohm, no vamos a decir mucho más por ahora. Si bien hay incógnitas
que surgirán a medida que avancemos, éstas serán resueltas llegado el momento. Hasta ese
momento, mejor que el lector viva en el feliz mundo del “V igual a I por R”, sin preguntarse
que quizás la ley expuesta no es tan simple como aparenta.
Capı́tulo 2
Elementos fundamentales
En esta sección se van a describir los 5 elementos más básicos de la teorı́a de circuitos, que
nos acompañarán largo y tendido por este divertido tour a través del mundo de los voltios y
los amperios. Son la resistencia, el condensador, la bobina, la fuente de tensión y la fuente de
corriente.
2.1.
Resistencia
Una resistencia es un elemento electrónico tal que si se le aplica una tensión a sus extremos,
por ella circula una corriente proporcional a dicha tensión siguiendo la ley de Ohm:
V = IR
Donde R es un parámetro propio de cada resistencia, cuya unidad es el Ohmio (Ω). Todo
material conductor tiene asociado un valor de resistencia. Sin embargo, en teorı́a de circuitos
no se suele trabajar con objetos de la calle para montar circuitos. No serı́a de mucha utilidad usar
la pata de una mesa o un filete de ternera como material conductor para las prácticas (aunque
todavı́a no lo he probado. Quizás funcione). Por ello se usan resistencias. Una resistencia viene
a ser entonces un elemento pequeñito que se comporta como un material conductor con una
cierta resistencia R. El valor de la resistencia viene a representar cuánta oposición muestra la
resistencia al paso de la corriente. A mayor resistencia, menos corriente circula por ella, y a la
inversa.
La resistencia R tiene un valor positivo, que va desde 0 hasta infinito teóricamente. En
la práctica no hay ni resistencias completamente nulas ni resistencias infinitas, si bien en el
papel, en los ejercicios, sı́ se puede dar el caso. Es por ello que vamos a analizar estos dos
casos extremos. Una resistencia nula, R → 0, es una resistencia que no opone ninguna
resistencia al paso de la corriente por ella. Este tipo de resistencias se llaman cortocircuitos,
y su comportamiento puede ser descrito según la Ley de Ohm. Sabemos que V = IR; si
ahora suponemos que R = 0, se deduce que V = 0, es decir, la diferencia de tensión que
hay entre los extremos de la resistencia es nula. ¿Qué quiere decir esto? Pues significa que la
diferencia entre las tensiones (o potenciales) es nula, lo cual sólo es posible si ambas tensiones
son iguales. Es decir, el potencial eléctrico no varı́a en los extremos de la resistencia, todo ello
independientemente de la corriente que por él circule. En la realidad, los cables que usamos
en el laboratorio (u otros), representan cortocircuitos, elementos conductores de resistencia
nula. Cuando se une con un cable dos puntos de un circuito, se dice que dichos puntos están
cortocircuitados, y como consecuencia están a la misma tensión.
Una resistencia infinita, R → ∞, es la que opone tanta resistencia al paso de corriente
que no deja pasar nada de corriente a través de ella, como se deduce de la ecuación de la
9
10
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
R
Resistencia
Cortocircuito Circuito abierto
Figura 2.1: casos lı́mites de resistencias
a
R
b
I
Figura 2.2: resistencia por la que circula una corriente de valor I
resistencia:
V
=0
R→∞ R
Lo que viene a decirnos que por la resistencia no circula nada de corriente. Ello tiene sentido si
tenemos en cuenta que resistencia significa oposición al paso de corriente. A mayor resistencia,
mayor oposición. Si la resistencia es infinita, la oposición es infinita, y por tanto no pasa nada
de corriente. Todo ello es independiente de la diferencia de tensión que soporta la resistencia.
No importa cuán grande es, pues la resistencia es tan grande que nunca podrá circular corriente
por ella. Este tipo de resistencia se conoce como circuito abierto. Su nombre deja bien claro su
naturaleza real: un circuito abierto se comporta exactamente igual que un cable que ha sido
cortado por la mitad, y cuyas mitades no están en contacto y lo suficientemente alejadas: las
cargas eléctricas no podrán saltar de un trozo del cable al otro, y por tanto no podrá haber
corriente eléctrica a través de él.
Sus respectivos sı́mbolos son los que representa la Figura 2.1.
A nivel energético, ¿qué ocurre en una resistencia? Vamos a pensar un poco. Sabemos que
la ecuación que rige el comportamiento de una resistencia viene dado por la ley de Ohm:
I = lı́m
Iab (t) =
Vab (t)
R
Supongamos la resistencia de la Figura 2.2.
La expresión de la potencia generada o consumida por la resistencia, siguiendo la fórmula
(1.3) es:
Vab (t)2
Vab (t)
Vab (t) =
(2.1)
P (t) = Iab (t)Vab (t) =
R
R
Donde se ha tenido en cuenta que, según la Ley de Ohm, Iab (t) = Vab (t)/R. Si nos damos
cuenta, la ecuación (2.1) siempre va a tomar un valor positivo. Ello se debe a que R es positiva,
y Vab (t)2 es positivo. Por tanto, el cociente será siempre un valor positivo. Como por tanto la
potencia de la resistencia adopta siempre un valor positivo, se deduce que la resistencia siempre
absorbe energı́a del medio, en este caso el circuito. La resistencia se comporta por tanto como
un elemento pasivo, ya que no aporta nada de energı́a al resto del sistema. Siempre la extrae
de él. ¿Qué ocurre con esa energı́a que absorbe la resistencia? La resistencia, en ese sentido,
es un elemento especial. A diferencia de otros elementos electrónicos que pueden devolver la
energı́a que han tomado de nuevo al circuito, la resistencia, la energı́a que consume, la disipa en
forma de calor. La potencia que la resistencia consume del circuito, por tanto, es igual al calor
que disipa. Otra expresión para la potencia en una resistencia se obtiene de (2.1) aplicando la
Ley de Ohm, V = IR.
Vab (t)2
P (t) =
= Iab (t)2 R
(2.2)
R
11
2.2. BOBINA
L
a
b
Figura 2.3: una bobina
Que es igualmente un valor siempre positivo, con lo cual la conclusión de que la resistencia es
un elemento pasivo no se ve alterada para nada.
Obtenida la expresión de la potencia, la expresión de la energı́a consumida por la resistencia
en un intervalo de tiempo [t0 ,t1 ] se puede expresar según la ecuación (1.4):
∆U =
Z
t1
t0
2
Iab (t) Rdt =
Z
t1
t0
Vab (t)2
dt
R
(2.3)
Recuérdese que la ecuación (2.3) representa la variación de la energı́a en el sistema (en este
caso la resistencia), entre los instantes t0 y t1 , es decir, ∆U = U(t1 ) − U(t0 ). Por tanto, el hecho
de que el signo de la ecuación (2.3) sea siempre positivo (ya que es la integral de una función
siempre positiva) indica que la energı́a en el instante t1 es mayor que la energı́a en el instante
t0 (∆U > 0 ⇒ U(t1 ) − U(t0 ) > 0 ⇒ U(t1 ) > U(t0 )), y por tanto el sistema, la resistencia, ha
ganado energı́a durante ese intervalo de tiempo.
2.2.
Bobina
Una bobina es un elemento formado por un conjunto de espiras muy próximas entre sı́, de
tal modo que se cumple que la relación que existe entre la corriente que la atraviesa y la tensión
que soporta es:
dIab
(2.4)
Vab (t) = L
dt
Donde de nuevo es necesario hacer resaltar que Vab (t) es la tensión que se mide del punto A al
punto B de la bobina (cada uno de ellos es un extremo), es decir, Va (t) − Vb (t), e Iab (t) es la
corriente que circula desde el punto A al punto B. Su sı́mbolo es el representado en la Figura
2.3.
La fórmula (2.4) es bastante más compleja que la fórmula que rige el comportamiento de
una resistencia. Ambas incluyen una constante de proporcionalidad. En las resistencias es el
valor R, y en la bobinas, es el valor L. L se conoce como inductancia de una bobina, y su
unidad es el Henrio (H). La inductancia de una bobina es una constante propia de cada, y rige
el comportamiento a modo de constante multiplicativa como indica la fórmula (2.4).
Dado que la fórmula (2.4) se basa en una derivada de la corriente respecto al tiempo, es
interesante estudiar qué ocurre en algunos casos especiales.
Si la corriente que atraviesa la bobina varı́a en el tiempo, la tensión que ésta soporta también
varı́a. Ahora bien, si nos encontramos el condiciones de corriente continua, donde las tensiones
y corrientes son constantes en el tiempo, ¿a qué se reduce la fórmula (2.4)?
Vab (t) = L
dconstante
dIab
=L
= L0 = 0 ⇒ Va (t) − Vb (t) = 0 ⇒ Va (t) = Vb (t)
dt
dt
Es decir, al ser constante la corriente que atraviesa la bobina, su derivada respecto al tiempo
es nula, y por tanto obtenemos que la diferencia de tensión que soporta la bobina es 0, o lo
que es lo mismo, la tensión en ambos extremos de la bobina es la misma, independientemente
de cuán grande es la corriente que circule (siempre que sea constante). ¿No nos suena esto de
antes? En efecto, lo que acabamos describir es el comportamiento de un cortocircuito, es decir,
12
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
a
L
b
a
b
Figura 2.4: bobina en condiciones de corriente continua
en condiciones de corriente continua, una bobina equivale a un cortocircuito, y son
intercambiables. La bobina puede ser ası́ sustituida por un cortocircuito que une los puntos
que antes se conectaban a la bobina, tal y como muestra la Figura 2.4.
Referente a la potencia en una bobina, el comportamiento de ésta es, en mucho, más rico
que el de una simple resistencia. La resistencia, como vimos, era un elemento pasivo: sólo era
capaz de tomar energı́a del medio (del circuito), pero no era capaz de devolverla. Esa energı́a,
además, se disipaba en forma de calor. Este comportamiento caracterı́stico de la resistencia es,
además, independiente del hecho de que se estén tratando tanto circuitos con señales variables
en el tiempo como circuitos de corriente continua: una resistencia siempre consume energı́a,
sean o no variables las señales medibles en el circuito.
La bobina muestra un comportamiento bastante distinto al de una resistencia. Si tomamos
la definición de potencia dada en la ecuación (1.3), obtenemos que la potencia generada o
consumida por una bobina es:
P (t) = Iab (t)Vab (t) = Iab (t)L
dIab
dIab
= LIab (t)
dt
dt
(2.5)
Lo que viene a decirnos que, para obtener la expresión de la potencia consumida o generada por
una bobina, habrá que obtener primero la derivada de la corriente que la atraviesa, multiplicarla
después por la misma corriente, y después por la inductancia de la bobina. Parece complejo,
pero en la realidad no lo es. Obsérvese además que, en caso de corriente continua, la expresión
de la potencia es igual a 0 (ya que incluye la derivada de una constante), lo cual tiene sentido si
pensamos que en corriente continua equivale a un cortocircuito y un cortocircuito no consume
energı́a (es una resistencia nula).
Es importante darse cuenta que la expresión de la potencia no nos da pistas acerca de
si la bobina es un elemento pasivo o un elemento activo. Los elementos pasivos, como las
resistencias, sólo pueden absorber energı́a del medio. Ahora bien, en una bobina, vemos que
la expresión P (t) depende de una derivada y del producto de una función Iab (t), que depende
del tiempo. Esa expresión, por tanto, podrá tomar tanto valores positivos como negativos
dependiendo del resultado de la derivada y de la expresión de I(t), y por tanto, una bobina,
dependiendo de la situación, puede comportarse como un elemento pasivo (P > 0, absorbe
energı́a), o activo (P < 0, desprende energı́a). De hecho, veremos algún ejemplo en el que la
bobina se comporta de forma periódica como elemento activo y pasivo, alternando entre uno y
otro.
¿Cómo varı́a la energı́a en una bobina? Obtenida la expresión de la potencia, la ecuación
(2.5), se puede usar la ecuación (1.4) para obtener cuál es la variación de la energı́a en una
bobina en un intervalo [t0 ,t1 ], es decir, ∆U = U(t1 ) − U(t0 ):
∆U = U(t1 ) − U(t0 ) =
=L
Z
Z
t1
t0
t1
L
Iab (t1 )2 − Iab (t0 )
2
t1
t0
"
Iab (t)dIab = L
t0
=
P (t)dt =
Z
Iab (t)
2
2
2
LIab (t)
dIab
dt
dt
#t1
t0
(2.6)
13
2.3. CONDENSADOR
a
C
b
Figura 2.5: un condensador
Esta ecuación representa la variación de la energı́a en la bobina entre los instantes t0 y t1 . Se
puede apreciar que la bobina puede ganar o perder energı́a dependiendo de si la corriente que
por ella circula aumenta o disminuye. Si la corriente que la atraviesa aumenta en el tiempo,
es decir, Iab (t1 ) > Iab (t0 ), entonces la expresión anterior toma un valor positivo, con lo cual
la energı́a en la bobina ha aumentado. Ahora bien, si la corriente disminuye, Iab (t1 ) < Iab (t0 ),
entonces la ecuación (2.6) toma un valor negativo, que significa que la bobina ha perdido
energı́a, que devuelve al resto del circuito en el que está.
2.3.
Condensador
Un condensador es un elemento electrónico constituido por dos placas conductoras, paralelas
y muy próximas entre sı́. Entre las placas se introduce un aislante que impide el movimiento
de cargas eléctricas de una placa a la otra.
No vamos a profundizar más acerca del condensador a nivel teórico, ya que es un elemento
que, a este nivel, deberı́a haberse estudiado ya.
La relación que existe entre la tensión que soporta un condensador y la corriente que por él
circula viene dada por la ecuación (2.7). Dicha ecuación, si bien distinta a la de las resistencias,
tiene similitudes que van más allá de lo que por ahora vamos a estudiar. Ya profundizaremos
en ello más tarde.
dVab
(2.7)
Iab (t) = C
dt
En la ecuación (2.7), Iab (t) es la corriente que circula desde el punto a al punto b del condensador
(a y b son los extremos del condensador), y Vab (t) es la tensión que se mide entre el punto a y
b del condensador, es decir, Va (t) − Vb (t).
Su sı́mbolo es el de la Figura 2.5.
La fórmula del condensador es también más compleja que la de la resistencia, y nos recuerda
a la de la bobina. Al igual que en los dos anteriores, hay una constante propia del condensador,
C, llamada Capacidad, cuyas unidades se miden en Faradios (F ). ¿Cómo se genera la corriente
que atraviesa a un condensador? Es más, ¿existe realmente una corriente que atraviesa al
condensador?
Sabemos que las placas de un condensador, formadas por material conductor, almacenan
cargas eléctricas. Concretamente, si a un condensador se le aplica una diferencia de tensión V
(o tensión a secas), entre sus extremos, cada placa almacenará una cantidad de carga Q igual
a:
Q = CV
Concretamente, cada placa del condensador almacena la misma cantidad de carga, pero cambiada de signo. Por tanto, una de las placas almacenará una cantidad de carga +Q, y la otra,
−Q.
Por tanto, si la cantidad de carga de cada placa depende de forma proporcional de la tensión
que soporta el condensador, es obvio que si dicha tensión varı́a en el tiempo, entonces la carga
de las placas también variará en el tiempo. Por tanto, se puede escribir:
Q(t) = CV (t)
(2.8)
14
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
Figura 2.6: generación de una corriente en un condensador
De tal modo que la carga de cada placa es igual al de la otra, pero de signo opuesto. Ahora
debemos pensar lo siguiente: si la tensión varı́a, varı́a la carga que almacena cada placa. Eso
será posible si llegan cargas a cada placa, o salen cargas de cada placa. Ese movimiento de
cargas provoca una corriente eléctrica que se puede obtener derivando la ecuación (2.8), ya que
la corriente es precisamente eso: cuánta carga atraviesa una superficie (sección de los conectores
del condensador) por unidad de tiempo, lo cual se obtiene derivando la ecuación citada:
I(t) =
dQ(t)
dV (t)
=C
dt
dt
Que es precisamente la ecuación (2.7) antes mencionada.
El problema del condensador es que no existe, como tal, una corriente I(t) que lo atraviesa.
Debemos recordar que entre las placas del condensador hay un material aislante que impide
que las cargas se muevan de una placa a otra. Existe una corriente generada en los terminales
de cada placa, pero esa corriente no llega a atravesar el condensador. En la práctica, eso no nos
supondrá problema: simplemente consideraremos que la corriente sı́ atraviesa al condensador.
En la Figura 2.6 se ve una representación gráfica de lo que ocurre cuando la tensión en el
condensador aumenta:
Por un lado, a la placa positiva del condensador (la que almacena la carga positiva), le
llegarán más cargas positivas. Ese movimiento de cargas genera una corriente en el sentido
indicado, es decir, el del movimiento de las cargas positivas (hacia el condensador), y cuyo
valor viene dado por la ecuación del condensador. Por otro lado, la placa negativa atraerá a
más cargas negativas, de modo que las cargas negativas generarán otra corriente. Ahora bien,
como la corriente tiene el sentido opuesto al del movimiento de cargas negativas, la corriente
que se genera tiene el mismo sentido que el de la corriente generada por las cargas de la placa
positiva. Su valor es el mismo, ya que la cantidad de carga en ambas placas es la misma.
Ası́ se explica lo que antes mencionábamos. Aunque a efectos prácticos, fuera del condensador,
parece que hay una corriente que lo atraviesa, en la realidad lo único que se produce es una
acumulación de cargas que simulan una corriente eléctrica que atraviesa el condensador, pero
que, en efecto, no lo hace.
Acabada la discusión de cómo se genera la corriente en un condensador, vamos a estudiar
lo que con él ocurre al igual que con la bobina. La corriente que atraviesa un condensador
sigue la expresión (2.7). Esa expresión depende, nuevamente, de una derivada, la derivada de
la tensión que soporta el condensador entre sus extremos. Si dicha tensión varı́a en el tiempo,
habrá corriente, pero, si no varı́a en el tiempo, como ocurre en condiciones de corriente
continua, la fórmula se reduce a:
Iab (t) = C
dVab
dconstante
=C
= C0 = 0
dt
dt
15
2.4. FUENTE DE TENSIÓN
C
a
b
a
b
Figura 2.7: condensador en condiciones de corriente continua
Es decir, si la tensión no varı́a en los extremos del condensador, como en corriente continua,
la corriente que lo atraviesa es nula, independientemente de cuánta tensión soporta el condensador (siempre que sea constante). De nuevo, vemos que esta definición ya la hemos visto con
anterioridad: se trata de un circuito abierto. El condensador, en corriente continua, se
puede sustituir por un circuito abierto, ya que son equivalentes, como se representa
en la Figura 2.7.
La potencia en un condensador muestra un comportamiento simular al de una bobina: un
condensador puede comportarse como elemento activo o pasivo, ya que puede tanto absorber
como devolver energı́a. Esto es fácilmente deducible de la ecuación (1.3):
P (t) = Iab (t)Vab (t) = C
dVab
Vab (t)
dt
(2.9)
Ya que P (t) depende de la derivada de Vab respecto del tiempo y de Vab (t), es evidente que
P (t) podrá tomar tanto valores positivos como negativos, comportándose como elemento activo
o pasivo dependiendo del caso. Además, si estamos en condiciones de corriente continua, P (t)
vale 0, ya que la derivada de Vab serı́a 0, y por tanto el consumo de energı́a serı́a nulo. Esto es
lo que cabrı́a de esperar, ya que en corriente continua, el condensador se comporta como un
circuito abierto, en el cual no se produce consumo de energı́a.
¿Cómo varı́a la energı́a en un condensador? Pues de un modo similar al de una bobina.
Supongamos que queremos hallar la variación de la energı́a de un condensador en un intervalo de
tiempo. Basta usar las ecuaciónes (1.4) y (2.9) para obtener dicha variación,∆U = U(t1 )−U(t0 ):
Z t1
Z t1
dVab
C
P (t)dt =
∆U = U(t1 ) − U(t0 ) =
Vab (t)dt
dt
t0
t0
"
#t1
Z t1
Vab (t)2
Vab (t)dVab = C
=C
2
t0
t0
=
C
Vab (t1 )2 − Vab (t0 )
2
2
(2.10)
Esta ecuación representa la variación de la energı́a en el condensador entre los instantes t0
y t1 . Se puede apreciar que el condensador puede ganar o perder energı́a dependiendo de si
la tensión que soporta aumenta o disminuye con el paso del tiempo. Si la tensión aumenta,
entonces Vab (t1 )2 > Vab (t0 )2 , con lo cual la ecuación (2.10) toma un valor positivo, es decir, el
condensador tendrı́a más energı́a (se comporta como elemento pasivo). Por contra si la tensión
disminuye, Vab (t1 )2 > Vab (t0 )2 , y por tanto la ecuación (2.10) adopta un valor negativo: el
condensador pierde energı́a, que entrega al resto del circuito, y se comporta como un elemento
activo. Que quede claro, ya que suele considerarse al condensador solamente como elemento
pasivo, pero, vemos, depende de la situación.
2.4.
Fuente de tensión
Una fuente de tensión, a nivel teórico, es un elemento electrónico capaz de imponer entre sus
extremos (terminales), una tensión determinada, independientemente de la corriente que por
16
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
+
+
+
−
-
-
Figura 2.8: fuente de tensión continua, constante en el tiempo (izquierda); fuente de tensión
genérica, constante o no en el tiempo (centro); fuente de tensión armónica (derecha)
+
−
AVV
+
−
ArI
Figura 2.9: fuentes de tensión dependientes
ella circule. Una fuente de tensión puede imponer entre sus terminales una tensión constante
o una tensión variable en el tiempo. Durante el análisis de circuitos en corriente continua
estudiaremos las fuentes constantes en el tiempo, si bien posteriormente entraremos de lleno
en el concepto de fuentes de tensión variables. Hay diversos modos de representar fuentes de
tensión. Algunos de ellos se recogen en la Figura 2.8.
Una fuente de tensión se dice que es dependiente si su valor de tensión es proporcional a
alguna tensión o corriente presente en el circuito donde se sitúa. El sı́mbolo de una fuente de
tensión dependiente puede ser igual al de una fuente normal, con la salvedad de que su valor
consiste en una expresión dependiente de alguna tensión o corriente del circuito. Por ejemplo,
en un circuito podrı́an aparecer las fuentes de tensión de la Figura 2.9.
La fuente de la izquierda es una fuente de tensión dependiente de tensión, lo que significa que
su valor de tensión es proporcional a otra tensión del circuito, siendo en su caso V . La constante
de proporcionalidad es Av , ası́ que la tensión que impone la fuente entre sus terminales es Av V .
La fuente de la derecha es una fuente de tensión dependiente de corriente, lo que significa
que su valor de tensión es proporcional a alguna corriente que hay en el circuito, siendo en su
caso I. La constante de proporcionalidad es Ar , ası́ que la tensión que impone la fuente entre
sus terminales es Ar I.
Las fuentes de tensión son elementos muy importantes dentro de los circuitos. Ya hemos
hablado previamente de elementos activos y elementos pasivos. Los activos aportan energı́a, de
la que se desprenden. Los pasivos absorben energı́a. ¿Qué es una fuente de tensión? Una fuente
de tensión, dentro de un circuito, puede comportarse como elemento activo o como elemento
pasivo. La diferencia fundamental con los elementos anteriormente estudiados, es que las fuentes
actúan como auténticos generadores de energı́a. Expliquemos esto con más detalle.
Las resistencias son elementos pasivos: consumen energı́a que extraen del circuito. Por otro
lado, las bobinas y condensadores pueden actuar tanto como elementos pasivos como elementos
activos, en el sentido de que pueden o bien absorber energı́a o bien desprender energı́a. La
cuestión fundamental al respecto es que las bobinas y condensadores no generan energı́a por
sı́ mismos. Cuando un condensador, por ejemplo, libera energı́a, es porque previamente la ha
absorbido del resto del circuito. Si bien formalmente las bobinas y condensadores se pueden
absorber y emitir energı́a, el término emitir se entiende en el sentido de emitir la energı́a que
previamente han absorbido, pero sin crearla.
Visto ası́, cabrı́a cuestionarse: si las resistencias absorben energı́a, y los condensadores y
bobinas sólo pueden liberar energı́a al resto del circuito si la han absorbido previamente: ¿de
dónde coño sale la energı́a? La respuesta es que la energı́a sale de las fuentes de tensión y de
las fuentes de corriente (éstas últimas las estudiaremos en la siguiente sección). Si bien en un
17
2.4. FUENTE DE TENSIÓN
+
5V
5mA
-
Figura 2.10: fuente de tensión con corriente que la atraviesa
a
+
V
b
Figura 2.11: fuente de tensión con su polaridad señalada
circuito una fuente de tensión puede actuar como elemento pasivo o activo, éstas son las que
aportan la energı́a al circuito y que permiten que todo funcione debidamente.
Si queremos hallar la potencia consumida o generada por una fuente de tensión, basta
aplicar la clásica fórmula (1.3), considerando cuál es la corriente que atraviesa a la fuente de
tensión, y por otro lado la tensión que ésta soporta entre sus extremos (coincidiendo esta última
exactamente con el valor de la fuente de tensión, con lo cual parte del trabajo ya lo tenemos
hecho sin necesidad de mucho esfuerzo). Supongamos la situación, por ejemplo, de la Figura
2.10:
Entonces, la potencia consumida o generada por la fuente es, siguiendo la ecuación (1.3):
P = 5 · 10−3 (−5) = 25 · 10−3 W
Donde se ha puesto −5V debido a que la tensión, como sabemos, se toma en el sentido de
circulación de la corriente. Como en este caso la corriente se mueve del polo negativo al positivo
de la baterı́a, la tensión que hay que medir es V− − V+ , que es −5V , como explicaremos a
continuación. Dado que la potencia es negativa, se deduce que la fuente está actuando como
un elemento activo, es decir, está suministrando energı́a al resto del circuito.
Por último hay que hacer referencia a los signos + y − de las fuentes de tensión. Dichos
signos representan la polaridad de la fuente. Al extremo con el signo + se le llama polo positivo, y
al extremo con el signo − se le llama polo negativo. La presencia de los polos es muy importante
para saber cómo funciona exactamente una fuente de tensión, ya que indica cómo es exactamente
la tensión que soporta la fuente. Supongamos que tenemos una fuente de tensión de valor V ,
como indica la Figura 2.11.
El que la polaridad de la fuente sea la dibujada implica que Va − Vb = V , es decir, la
polaridad de la fuente nos dice que la diferencia de tensión entre el polo positivo y el
polo negativo es igual al valor de la fuente de tensión. Es decir,
V+ − V− = V alor de la f uente
Esto último es de vital importancia. Lo pondrı́a a letra de tamaño 100 para expresar la importancia de tal hecho, pero estropearı́a la estética del documento, ası́ que me conformo con la
negrita. Pero no se olvide: es muy importante.
Es de ahı́ de donde, en el ejemplo de antes, obtuvimos el valor de tensión de −5V . En el
ejemplo anterior quisimos medir la diferencia de tensión V− − V+ . En principio, la fuente de
18
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
a
V
b
Figura 2.12: fuente de tensión sin polaridad señalada
I
Figura 2.13: fuente de corriente
tensión nos decı́a que V+ − V− = 5V , ası́ que, ¿cuánto valı́a V− − V+ ? Muy fácil:
V− − V+ = −(V+ − V− ) = −5V
De ahı́ el valor de tensión de −5V antes utilizado.
Notemos además que en las fuentes de tensión como la representada en la Figura 2.12 se
cumple la lı́nea grande representa el polo positivo y la lı́nea pequeña el polo negativo. Por tanto,
en la figura, sin necesidad de especificar con signos + y − cuáles el polo positivo y el negativo,
deberı́amos ser capaces de deducir que. Este tipo de representación es más común que la que
representa de forma implı́cita el polo positivo y el polo negativo de la fuente de tensión, en
fuentes de tensión continuas. En las fuentes de tensión variables en el tiempo la polaridad debe
representarse siempre. En suma, la polaridad de una fuente debe estar representada sin ningún
tipo de ambigüedad, ya que la ésta determina el comportamiento de la fuente. Por ejemplo, el
circuito donde se situase la fuente de la Figura 2.12 tendrı́a un comportamiento completamente
distinto si la polaridad fuera la contraria a la mostrada en la figura. A pesar de ello, muchas
veces el lector podrá ver que en un circuito no se representa la polaridad de una fuente. Eso,
salvo en fuentes de tensión continua como la de la Figura 2.12 donde la polaridad se puede
deducir del dibujo, es un error, y deberı́a evitarse a toda costa.
2.5.
Fuente de corriente
Una fuente de corriente, a nivel teórico, es un elemento electrónico capaz de hacer que
por ella circule una corriente determinada independientemente de la tensión que soporte. Una
fuente de corriente generar una corriente constante en el tiempo o variable. Durante el análisis
de circuitos en corriente continua estudiaremos las fuentes constantes en el tiempo, si bien
posteriormente entraremos de lleno en el concepto de fuentes de corriente variables. Una fuente
de corriente se representa generalmente como aparece en la Figura 2.13.
Donde es importante destacar que la corriente que la fuente genera tiene el
sentido indicado por la flecha de la fuente, y el valor de la fuente (I).
Una fuente de tensión se dice que es dependiente si su valor de corriente es proporcional
a alguna tensión o corriente presente en el circuito donde se sitúa. Una fuente de corriente
dependiente tiene un sı́mbolo algo distinto al de una fuente normal: en vez de ser redonda,
tiene forma de rombo, si bien también es normal verlas dibujadas como fuentes de corriente
2.6. PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA
AgV
19
AiI
Figura 2.14: fuentes de corriente dependientes
normales en las que su valor de corriente tiene forma de expresión dependiente. La Figura 2.14
representa dos fuentes dependientes, una de tensión, y otra de corriente.
La fuente de la izquierda es una fuente de corriente dependiente de tensión, lo que significa
que su valor de corriente es proporcional a otra tensión del circuito, siendo en su caso V . La
constante de proporcionalidad es Ag , ası́ que la corriente que por ella fluye es Ag V .
La fuente de la derecha es una fuente de corriente dependiente de corriente, lo que significa
que su valor de corriente es proporcional a alguna corriente que hay en el circuito, siendo en su
caso I. La constante de proporcionalidad es Ai , ası́ que la tensión que impone la fuente entre
sus terminales es Ai I.
Al igual que en el caso de las fuentes de tensión, una fuente de corriente puede actuar como
elemento pasivo o activo. Ahora bien, al igual que con las fuentes de tensión, las fuentes de
corriente tienen la capacidad de generar energı́a por ellas solas. No la deben recibir previamente
de algún otro medio, como en el caso de las bobinas o condensadores.
La expresión de la potencia consumida o generada por una fuente de corriente se obtiene
directamente aplicando la fórmula (1.3), considerando que en este caso, el valor de la corriente
que hay que utilizar ya lo conocemos de forma anticipada, puesto que es el que indica la misma
fuente de corriente.
2.6.
Principio de conservación de la energı́a
En cualquier circuito, si se desprecian fenómenos de radiación, se cumple el principio de
conservación de la energı́a: la energı́a consumida por todos los elementos pasivos en un determinado periodo de tiempo debe ser igual a la energı́a que suministran los elementos activos en
el mismo periodo de tiempo.
Ello equivale a decir que, en cualquier instante de tiempo, la potencia que generan los
elementos activos es igual a la potencia consumida por los pasivos.
20
CAPÍTULO 2. ELEMENTOS FUNDAMENTALES
Capı́tulo 3
Leyes de Kirchhoff
He aquı́ todo el meollo de la cuestión. Dos son los lemas o leyes de Kirchoff y, en base a
ellos, y en base a su validez en todo lo que estudiaremos de ellas, podremos analizar más o
menos eficientemente un circuito y conocer ası́ sus parámetros más caracterı́sticos: tensión y
corriente.
Primeramente, antes de explicar cada una de las Leyes de Kirchoff, es necesario dar una
serie de conceptos que aparecen dentro de las Leyes de Kirchoff, y en general, dentro del mundo
de la teorı́a de circuitos.
3.1.
Conceptos previos
Un circuito es un conjunto de elementos electrónicos (ya sean los que hemos estudiado u
otros distintos), que están conectados entre sı́ mediante conductores adecuados. Seguramente se
podrı́a discutir acerca de esta definición de circuito. Es más, posiblemente sea la más imprecisa
e inexacta del universo, pero para lo que nos compete, es suficiente como para salir adelante.
Un nudo o nodo es aquél punto de un circuito donde confluyen, al menos, dos terminales
(extremos), de dos elementos distintos.
Es importante hacer hincapié en que han de confluir dos terminales o más, es decir, dos ya
son suficientes para dar lugar a un nudo. La Figura 3.1 representa un circuito con varios nudos.
En el circuito de la Figura 3.1 se hay 6 nudos, los puntos A, B, C, D, E y F. El nudo A
es el nudo en el que se juntan los extremos de la fuente de tensión V y de la resistencia R1 .
En el nudo B se juntan tres terminales: uno de los de la resistencia R1 , otro del condensador
C1 y otro terminal de la resistencia R2 . En el nudo C confluyen tres terminales: un terminal
de la bobina L1 , otro del condensador C2 y otro de la resistencia R2 . En el nudo D se juntan
dos terminales: uno del condensador C2 y otro de la bobina L2 . En el nudo E se juntan tres
terminales: uno de la fuente de tensión V , otro del condensador C1 , y otro del cortocircuito que
conecta E y F1 . En el nudo F se jutan tres terminales: uno de la bobina L1 , otro de la bobina
L2 , y otro del cortocircuito que conecta E y F.
Se dice que un nudo es un nudo principal si en él confluyen 3 o más terminales de elementos
del circuito. En el ejemplo anterior los nudos principales son B, C, E y F.
Un tema especialmente delicado a la hora de trabajar con circuitos es la posibilidad de
redibujar ciertas de sus partes. La idea es poder redibujar algunas zonas del circuito, de modo
que su comportamiento no varı́e. Si bien esto nos puede parecer una idea poco intuitiva (si
cambiamos el circuito, ¿no deberı́a comportarse de un modo distinto?), puede hacerse en gran
cantidad de ocasiones. Un claro ejemplo de esta idea es la posibilidad de redibujar los cables del
circuito (todo lo que sea cortocircuito), siempre que las conexiones entre elementos (distintos
1
Recuérdese que un cortocircuito es un caso extremo de una resistencia (una resistencia de valor 0) y por
tanto es un elemento electrónico tan legı́timo como otro cualquiera.
21
22
CAPÍTULO 3. LEYES DE KIRCHHOFF
V
V
A
R1
A
B
R2
E
F
L2
D
Figura 3.1: un circuito con diversos
nudos
C1
B
R2
L1
C
C2
R1
C1
G
L1
C
C2
L2
D
Figura 3.2: el circuito de la Figura
3.1, redibujado
de cortocircuitos) no varı́en, es decir, que ni se creen nuevas conexiones ni se destruyan
conexiones existentes. Nótese que el término redibujar usado anteriormente significa redibujar
de cualquier modo, siempre que, repetimos, no se alteren las conexiones entre elementos.
Por ejemplo, el circuito de la Figura 3.1 serı́a equivalente al de la Figura 3.2. En dicha figura
puede apreciarse que el circuito se ha redibujado. Es más, el cortocircuito situado entre E y F
se ha eliminado completamente. Lo importante es darse cuenta de que, en efecto, las conexiones
entre componentes (distintas de cortocircuitos) se mantienen inalteradas: el terminal derecho de
la fuente V , del condensador C1 , de la bobina L1 y de la bobina L2 , siguen estando conectados
entre sı́ (es decir, están cortocircuitadas).
Puede que esto parezca una idea algo estúpida, pero debe quedar clara, ya que hay circunstancias en las que se redibujan circuitos para intentar facilitar su compresión, o bien para
destacar alguna cualidad que tiene. Que nadie se sienta asustado por redibujar un circuito de
otra manera a la original siempre que las conexiones entre componentes se mantengan inalteradas.
Una rama es cualquier camino del circuito comprendido entre dos nudos principales consecutivos. En el ejemplo anterior, son ramas los siguientes caminos:
• B-A-E.
• B-C.
• B-E.
• C-D-F.
• C-F.
• E-F.
En cambio, no son ramas, por ejemplo, los caminos B-C-D, A-B-E o E-F-D.
Una propiedad muy importante de cualquier rama es que, independientemente de los elementos que haya en ella, por todos sus puntos circula la misma corriente.
En el circuito de la Figura 3.3 hemos considerado las corrientes I1 e I2 . La corriente I1 es
la que circula por la rama A-C-D, y la corriente I2 es la que circula por la rama B-D. En la
rama A-C-D se da una situación a la que nos enfrentaremos en muchas situaciones: en ella hay
23
3.1. CONCEPTOS PREVIOS
C
I1
A
D
I2
B
Figura 3.3: un circuito con corrientes en sus ramas
un circuito abierto. Como sabemos que por los circuitos abiertos no puede circular nada de
corriente, entonces se puede deducir que la corriente que circula por el circuito abierto es nula.
Ahora bien, como hemos dicho que por todos los puntos de una misma rama circula la misma
corriente, y el circuito abierto está en la rama A-C-D, también se deduce que la corriente I1 es
nula (por tanto tampoco circula corriente por la resistencia que hay entre los puntos A y C). Por
otro lado, la corriente I2 es la corriente de la rama B-C. Como en esa rama hay dos elementos,
un condensador y una bobina, se deduce que la corriente que circula por el condensador es
igual a la corriente que circula por la bobina. Esta caracterı́stica es muy importante ya que nos
permite establecer ecuaciones del estilo:
Corriente en bobina = Corriente en condensador
Una malla es cualquier sucesión de ramas que forman un camino cerrado, y sin pasar por
ningún nodo dos veces, a excepción del primero y el último, que son los que abren y cierran la
malla. La Figura 3.4 representa un circuito con un total de 6 mallas.
En dicho circuito, son mallas las siguientes:
• Malla 1: B-C-H-A-B.
• Malla 2: C-F-G-H-C.
• Malla 3: D-E-F-C-D.
• Malla 4: B-C-F-G-H-A-B.
• Malla 5: H-C-D-E-F-G-H.
• Malla 6: A-B-C-D-E-F-G-H-A.
Si bien se aprecia una importante cantidad de mallas, no todas son de utilidad. Una malla
es de interés si ésta no contiene a otras mallas. Por ejemplo, las mallas 1, 2 y 3 son mallas de
interés, pero las mallas 4, 5 y 6 no son de interés, porque engloban a otras mallas (por ejemplo,
la malla 4 engloba a la malla 1 y a la malla 2).
Hecha esta pequeña revisión de conceptos necesarios para comprender las Leyes de Kirchoff,
pasamos a enunciarlas.
24
CAPÍTULO 3. LEYES DE KIRCHHOFF
D
E
C
B
A
F
G
H
Figura 3.4: un circuito con diversas mallas
I2
I3
I1
I4
Figura 3.5: un nudo al que llegan y del que salen diversas corrientes
3.2.
Ley de los nudos
La ley de los nudos dice:
La suma de todas las corrientes que entran en un nudo es igual a la suma de
todas las corrientes que salen de ese nudo.
Pongamos un ejemplo para entender mejor el funcionamiento de esta ley. Supongamos el
nudo de la Figura 3.5:
En este nudo, las corrientes que entran son I1 , I2 e I4 , y la única corriente que sale es I2 .
Apliquemos ahora, al nudo la ley de los nudos. Esta ley se aplica de forma directa: no hay que
pensar demasiado. Simplemente se suman las corrientes que entran, y se igualan a la suma de
las corrientes que salen. Si en algún caso no entra o no sale ninguna corriente, la suma es igual
a cero. La ecuación asociada al nudo es:
I1 + I3 + I4 = I2
Supongamos ahora un circuito pequeño, como el de la Figura 3.6.
Vamos a pensar lo que ocurre en este circuito. Sabemos que la corriente circula de donde hay
más tensión a donde hay menos tensión. Sabemos además que en este circuito hay una rama,
o malla. Sı́, ya sé que no hay nudos principales, por tanto no se puede aplicar la definición
de rama antes dada, pero lo cierto es que éste es un caso especial: lo que hay ahı́ arriba se
puede entender como una única rama o como una malla. Por tanto, sabemos que por toda
ella circula la misma corriente. ¿En qué sentido circula esa corriente? Como sabemos que la
corriente, a través de resistencias, va de donde hay más tensión a donde hay menos tensión,
la corriente de esa rama se debe mover en el sentido de la corriente I3 (según la fuente de
tensión,Va − Vc = 5V RightarrowVa > Vc ). Por tanto podemos pensar que, en el nudo B, las
corrientes que haya van a tener el sentido de circulación de la corriente I3 . Esas corrientes son
25
3.2. LEY DE LOS NUDOS
A
I2
R1
5V
B
I3
R2
I1
C
Figura 3.6: un ejemplo de la ley de los nudos
B
R1
R5
A
C
R4
R6
R3
V1
E
R2
D
V2
Figura 3.7: un circuito más complejo al que aplicar la ley de los nudos
I1 e I2 . Por tanto, aplicando la ley de los nudos, y considerando que I1 es la corriente que sale
e I2 es la que entra, se deduce que:
I1 = I2
Lo cual nos tranquiliza, pues sabemos, como habı́amos dicho anteriormente, que al haber usa
sola rama, la corriente por todos sus puntos deberı́a ser la misma, y por tanto la igualdad
I1 = I2 era necesaria.
Hasta ahora somos felices, pero, ¿qué ocurre en circuitos más complejos? Vamos a suponer
un circuito bastante más complejo que el de antes, por ejemplo, el de la Figura 3.7.
Hasta aquı́ ha llegado nuestra felicidad. Intentemos aplicar la ley de los nudos al nudo A.
Uf. Joder. Mierda. Tras estas tres cortas palabras, pensamos un poco. Para poder aplicar la
ley de los nudos, necesitamos saber cuáles son los sentidos de las corrientes del nudo que se
está analizando, para ası́ poder determinar cuáles son las que entran y cuáles son las que salen.
En el ejemplo anterior fue relativamente fácil deducir cuáles eran los sentidos de movimiento de
las corrientes que circulaban por el nudo A. Pero, en este ejemplo eso no es una tarea trivial.
En el nudo A va a haber tres corrientes: la que va por B-A, la que va por C-A, y la que va por
D-A. Pero, ¿qué sentidos de movimiento tienen dichas corrientes? Ahora no podemos deducir
de forma inmediata que en B va a haber más tensión que en A, o que en A va a haber menos
tensión que en C, etc., ya que la estructura del circuito es sensiblemente más compleja que la
del circuito del ejemplo anterior. Ası́ pues, ¿es que acaso no vamos a poder aplicar la ley de los
nudos a circuitos moderadamente complejos? La respuesta es que sı́, que sı́ vamos a poder (si
no, entre otras cosas, no habrı́a explicado la ley de los nudos). La pregunta es, cómo.
Pues bien, existe una verdad absoluta en teorı́a de circuitos, que no se va a
demostrar (aunque tampoco es muy complejo de probar), que nos dice que, a la
hora de resolver un circuito, podemos suponer que las corrientes que por sus ramas
26
CAPÍTULO 3. LEYES DE KIRCHHOFF
B
R1
R5
A
I3
I1
I2
R3
V1
E
R2
C
D
R6
R4
V2
Figura 3.8: al final no resultó ser tan complicado...
circulan tiene un sentido arbitrario, o lo que es lo mismo, que circulan con el sentido
que nos da la gana. Nosotros elegimos sus sentidos de circulación. Eso sı́, una vez
que se ha fijado un sentido para cada corriente, hay que ser consecuente a él, y no
modificarlo conforme nos dé la gana.
Lo de ser consecuente se refiere a situaciones como la siguiente. Si hemos decidido suponer
que una corriente circula de un punto D a un punto F a través de una resistencia R, según la
ley de Ohm su expresión serı́a:
VDF
VD − VF
IDF =
=
R
R
Pero no serı́a:
VF − VD
VF D
=
IDF =
R
R
Es decir, tal y como explicamos con anterioridad, la diferencia de tensión está determinada
por el sentido de circulación de la corriente, y es igual a la tensión en el punto de origen de
la corriente menos la tensión en el punto de destino de la corriente. Lo mismo ocurre con las
fórmulas de la bobina y del condensador, como ya se explicó en su momento.
Ası́ pues, en nuestro ejemplo podrı́amos suponer que las corrientes que van por las resistencias tiene los sentidos dibujados en la siguiente Figura 3.8 (pero, hay que insistir en ello,
podrı́amos haber elegido otros sentidos completamente distintos).
Establecidos los sentidos de circulación para las corrientes relativas al nudo A, se puede
escribir, según la ley de los nudos, que:
I1 + I2 + I3 = 0
Ya que todas las corrientes entran al nudo, pero ninguna sale de él (por tanto su suma es cero).
Si ahora se aplica la Ley de Ohm para cada corriente, obtenemos:
VBA
VB − VA
=
R1
R1
VCA
VC − VA
I2 =
=
R5
R5
VD − VA
VDA
=
I3 =
R3
R3
I1 =
Con lo que la ecuación del nudo A, sustituyendo los valores de corriente hallados, serı́a:
VB − VA VC − VA VD − VA
+
+
=0
R1
R5
R3
Obtenida esta ecuación serı́an todavı́a necesarias otras tantas para poder resolver el circuito
que tenemos entre manos. Entraremos en detalle en las sección 5.2, más adelante.
3.3. LEY DE LAS MALLAS
27
Como último detalle, y se trata de algo que no tiene que ver con la ley de los nudos, vamos
a fijarnos en la toma de tierra que hay colocada en el circuito. La toma de tierra está conectada
al lado del punto E. Sabemos que el punto E está a la misma tensión que el polo negativo de
la fuente de tensión, ya que están unidos por un cortocircuito (un cable pelado y mondado, sin
ningún elemento entre medias), y que el punto E está unido, también mediante un cortocircuito,
a la toma de tierra. Es por ello que tanto el punto E como el polo negativo de la fuente de
tensión están a 0 voltios: la toma de tierra dicta que allı́ hay 0 voltios, y por tanto todos los
puntos que estén cortocircuitados a ella estarán a 0 voltios. También sabemos que la fuente de
tensión establece que V+ − V− = V1 , o lo que es lo mismo, VB − VE = V1 . Como VE = 0, tal y
como hemos deducido, entonces obtenemos que VB = V1 . Dicho de otro modo, ya conocerı́amos
la tensión en el punto B (polo positivo de la fuente de tensión). En muchos circuitos, en
general, hay que plantear las ecuaciones que imponen las fuentes de tensión para
poder resolverlos.
El mismo razonamiento no se podrı́a hacer con la fuente de tensión de V2 voltios, ya que el
punto D (polo negativo de esa fuente), no está cortocircuitado a la toma de tierra, puesto que
hay una resistencia entre medias. Es por ello que no se puede asegurar que en D haya 0 voltios,
y por ende no se pueda deducir, del mismo modo que con la fuente de V1 voltios, que en el polo
positivo haya V2 voltios.
3.3.
Ley de las mallas
Dice ası́ la ley de las mallas:
La suma algebraica de todas las tensiones (diferencias de tensión) a lo largo de
una malla, que se recorre en un determinado sentido, es igual a cero.
Esta ley es, en una primera impresión, más complicada que la ley de los nudos, si bien ambas
son equivalentes y valen de igual modo para resolver circuitos.
¿Qué significa el término algebraica que aparece en el enunciado de la ley de las mallas? El
término algebraica viene a decirnos que, cuando se escriban las ecuaciones correspondientes a
cada malla, las tensiones que en ellas aparecen deberán estar precedidas de un signo + o −. En
primer lugar, se deben determinar corrientes de rama, es decir, al igual que con la ley de los
nudos, se deben definir las corrientes que circulan por las ramas del circuito, con los sentidos de
circulación que se quiera. Definir una corriente con un sentido determinado implica determinar
si una tensión, en la ley de las mallas, será considerada positiva o negativa. Concretamente,
establecidas las corrientes para cada rama, hay que recorrer todas las mallas (preferiblemente
mallas indivisibles, es decir, las que definı́amos como aquellas que no contenı́an a otras mallas
más pequeñas). Para cada malla, se debe definir un sentido de recorrido, horario o antihorario. Establecido el sentido de recorrido de la malla, se obtiene una ecuación de malla,
resultado de aplicar la ley de las mallas. En cada malla habrá una serie de diferencias de
tensión que deberá de tener en cuenta la ley de las mallas. Cada diferencia de tensión viene
determinada por un elemento electrónico, es decir, allı́ donde haya un elemento electrónico,
ya sea una resistencia, un condensador, o una fuente de tensión por poner algunos ejemplos,
habrá una diferencia de tensión que la ecuación de la malla deberá de incorporar. Además, esas
diferencias de tensión irán acompañadas por un signo + o − dependiendo de:
• Si el elemento es una resistencia, condensador o bobina, entonces el signo es − si la
corriente que atraviesa dicho elemento (la que nosotros presumimos previamente) coincide
con el sentido de recorrido de la malla. En caso contrario, el signo es +.
28
CAPÍTULO 3. LEYES DE KIRCHHOFF
R1
R2
+
−
Vg1
+
−
R3
Vg2
R4
+
−
R5
R6
Vg3
Figura 3.9: un sencillo circuito al que aplicar la ley de las mallas
R1
A
+
−
Vg1
D
R2
B
I3
I1
I2
R3
R4
C
+
−
Vg2
R5
E
I4
+
−
G
Vg3
F
I5
I6
R6
Figura 3.10: método para aplicar la ley de las mallas al circuito de la Figura 3.9
• Si el elemento es una fuente (ya sea de tensión o de corriente), entonces el signo es − si el
sentido de recorrido nos lleva de su polo + a su polo −, y positivo si el sentido de recorrido
nos lleva de su polo − a su polo +. Referente a la polaridad (signo + y −) de una fuente
de corriente, este aspecto lo explicaremos más adelante en mayor detalle (sección 5.3).
Consideremos entonces el circuito de la Figura 3.9.
Según lo explicado, en primer lugar hay que definir corrientes en cada una de las ramas. Corrientes con los sentidos de circulación que nos de la gana. En nuestro caso, son los representados
en la Figura 3.10.
Establecidas las corrientes de la figura anterior, ahora podrı́amos aplicar la ley de las mallas
a cada una de las tres mallas pequeñas del circuito.
En la malla de arriba a la izquierda, malla A-B-E-D-A, establecerı́amos un sentido de
recorrido de la malla. El sentido, en este caso, va a ser anti-horario. Fijado el sentido antihorario, vemos que la ecuación de malla serı́a la siguiente:
−Vg1 + VR4 − VR3 − VR1 = 0
Donde cada VRi representa la diferencia de tensión en cada resistencia según las corrientes
dibujadas. Si aplicamos ahora la Ley de Ohm, la ecuación anterior se transformarı́a en:
− Vg1 + I4 R4 + I3 R3 − I1 R1 = 0
(3.1)
29
3.3. LEY DE LAS MALLAS
Y es necesario recalcar otra vez la concordancia que tiene que haber entre los sentidos de
circulación de las corrientes y las diferencias de tensión a la hora de aplicar la Ley de Ohm. En
este caso ello implica que:
VR4 = VE − VD = I4 R4
VR3 = VB − VE = I2 R3
VR1 = VA − VB = I1 R1
En la malla de arriba a la derecha, malla B-C-F-E-B, establecerı́amos otro sentido de recorrido
aleatorio, en este caso, horario. Fijado el sentido horario, la ecuación de malla que se obtendrı́a
serı́a la siguiente:
− VR2 − Vg2 + VR5 + VR3 = 0
(3.2)
Donde nuevamente, aplicando la Ley de Ohm a cada resistencia:
I3 R2 − Vg2 + I5 R5 + I2 R3 = 0
Y nuevamente, según los sentidos de las corrientes dibujadas, las diferencias de tensión serı́an:
VR2 = VB − VC = I3 R2
VR5 = VE − VF = I5 R5
VR3 = VB − VE = I2 R3
En la malla de abajo, la malla D-F-G-D, establecerı́amos un sentido de recorrido, por ejemplo
anti-horario, obteniendo ası́ la siguiente ecuación de malla:
−Vg3 + VR6 + VR5 − VR4 = 0
Que se transformarı́a, según la Ley de Ohm, en:
− Vg3 + I6 R6 + I5 R5 − I4 R4 = 0
(3.3)
De nuevo, según los sentidos de las corrientes dibujadas, esas diferencias de tensión serı́an:
VR6 = VF − VG = I6
VR5 = VE − VF = I5
VR4 = VF − VD = I4 R4
El problema tras aplicar la ley de las mallas es que, como resultado, obtenemos tres ecuaciones, (3.1), (3.2) y (3.3), con 6 incógnitas,I1 , . . . , I6 . Es obvio que algo nos falta para poder
obtener nuestras incógnitas, concretamente tres ecuaciones en las que aparezcan las variables
I1 , . . . , I6 . Esas ecuaciones se podrı́an obtener del mismo circuito al aplicar la ley de los nudos,
y ası́ obtener, por ejemplo:
I1 + I2 + I3 = 0
I2 = I4 + I5
I3 + I5 = I6
(3.4)
(3.5)
(3.6)
Con estas ecuaciones se tendrı́a un sistema de 6 ecuaciones ((3.1), (3.2), (3.3), (3.4), (3.5), (3.6))
y 6 incógnitas, que nos darı́a la solución a nuestro problema, las variables I1 , . . . ,I6 .
El problema hasta el momento parece evidente: si para un circuito tan simple ya tenemos
un sistema de 6 ecuaciones con 6 incógnitas, es probable que prefiramos pudrirnos de asco antes
que continuar con circuitos más complejos. Concretamente, este método para resolver circuitos
consistente en mezclar las ecuaciones de la ley de las mallas y la ley de los nudos es un método
que apenas se utiliza. Dirı́a que sólo los masocas lo hacen.
Existen otros dos métodos que, aun basándose igualmente en las leyes de Kirchoff, son
mucho más eficientes, pero antes de entrar en su análisis, nos fijaremos en otro concepto que
nos puede simplificar el análisis de circuitos, las asociaciones de elementos.
30
CAPÍTULO 3. LEYES DE KIRCHHOFF
Capı́tulo 4
Asociaciones de elementos
4.1.
Concepto de asociación de elementos
El problema de las asociaciones de elementos consiste en intentar simplificar determinadas
distribuciones de elementos en un circuito, sustituyéndolas por equivalentes que faciliten el
trabajo.
Para entendernos, pretendemos sustituir determinados elementos por uno que se dice equivalente, en el sentido de que el circuito externo a dichos elementos muestra el mismo comportamiento tanto si se toma el circuito original como si se toma el circuito en el que esos elementos
han sido sustituidos por el elemento equivalente.
Por ejemplo, supongamos el circuito de la Figura 4.1. Si en dicho circuito a nosotros nos
interesase hallar la corriente que circula por R, llamada I, en principio parece ser que las
resistenciasserı́an un poco liosas y que nos dificultarı́an la labor que tenemos entre manos.
Pues bien, existe una resistencia equivalente a todas ellas, que llamaremos Req , tal que, si
todas las resistencias entre los puntos A y B (y hacia la derecha), es decir, R1 , . . . , R4 , son
sustituidas por esa Req , entonces el circuito externo a todas ellas, en este caso la resistencia R
y la fuente de tensión V , muestra un comportamiento idéntico al circuito que contiene todas las
resistencias. Como el comportamiento es el mismo, entonces la corriente I que circula a través
de R serı́a igual a la que hay en el circuito original, y por tanto, tanto nos darı́a hallar a I
usando la resistencia equivalente o usando el circuito original. Dicho de otro modo, tendrı́amos
dos circuitos a partir de los cuales hallar I, tal y como muestra la Figura 4.2, donde parece
obvio que es más fácil hallar I siguiendo el circuito (2) que el circuito (1).
Vemos, pues, que el concepto de asociaciones de elementos no es algo que haya nacido para
molestarnos, sino para simplificarnos el análisis de circuitos. Cuando se coge experiencia en ello,
es difı́cil encontrar un circuito en el que no se lleven a cabo asociaciones de elementos con las
que simplificar el análisis.
R
A
R1
I
R2
V
B
R3
R4
Figura 4.1: un circuito que simplificar
31
32
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
Estructuras equivalentes
R
R1
A
R
I
V
A
I
R2
R3
V
Req
R4
B
(1)
B
(2)
Figura 4.2: relación entre el circuito original y el circuito simplificado
R1
A
R2
B
R3
R4
Figura 4.3: resistencias que asociar
Ahora toca responder a la pregunta del millón, a saber, cómo se obtienen elementos equivalentes a un conjunto de elementos. ¿De dónde tetas sacarı́amos la resistencia Req antes mencionada, por citar un ejemplo?
Vamos a replantear más formalmente el problema de los elementos equivalentes. Nuestro
propósito es el de obtener un elemento equivalente a otra serie de elementos más compleja.
Partiremos de la base de que la parte compleja de la que obtener el equivalente tiene dos
terminales externos que la conectan al resto del circuito. Por ejemplo, en el ejemplo
anterior, la parte de la que obtener el equivalente, y que tiene dos terminales externos, es la
representada en la Figura 4.3.
Esa es la parte que anteriormente sustituimos por una resistencia equivalente. Como vemos,
esta serie de elementos tiene dos terminales externos, que lo conectan al resto del circuito. Esos
terminales están señalados como los puntos A y B.
El elemento equivalente, a su vez, también tiene dos terminales externos, siendo el representado en la Figura 4.4.
Ahora queda plantear de forma más formal cuándo ambos modelos son equivalentes. ¿Existe
realmente una condición que los haga equivalentes a efectos prácticos, en el sentido de que si
se sustituye uno por otro, el resto del circuito no altera su funcionamiento? Pensemos un poco.
Sabemos que el modelo original tendrá un comportamiento determinado por su estructura, y
que se puede resumir en que, si se le aplica una tensión a sus terminales de entrada y de salida,
habrá una corriente de entrada y de salida por dichos terminales, es decir, habrá una corriente
que entre por un terminal y salga por el otro. Esa corriente estará determinada por la tensión
aplicada y por la configuración de resistencias que forman el circuito del que se quiere hallar el
equivalente, de modo que habrá una ecuación que relacione la tensión aplicada y la corriente
4.1. CONCEPTO DE ASOCIACIÓN DE ELEMENTOS
33
A
Req
B
Figura 4.4: resistencia equivalente
de entrada y de salida. Si fuéramos capaces de conseguir que el modelo equivalente, en nuestro
ejemplo la resistencia Req , tuviera la misma relación entre la tensión en sus terminales y las
corrientes de entrada y de salida, entonces podrı́amos decir que es equivalente al modelo
original. En efecto, todo lo situado fuera del modelo equivalente no notará diferencia alguna
entre el modelo equivalente y el original, ya que aquello que rige su comportamiento (el del
modelo equivalente), a saber, la relación entre la tensión entre sus terminales y las corrientes
de entrada y de salida, serı́a igual al del modelo original.
Por tanto, en términos menos filosóficos y más sencillos, se puede decir que dos circuitos,
cada uno con dos terminales externos, serán equivalentes si la relación existente
entre la tensión en los terminales y las corrientes de entrada y salida son la misma
para ambos circuitos. Esta es una condición necesaria y suficiente para que dos circuitos
sean equivalentes. Todos los circuitos equivalentes la cumplen, y si dos circuitos cualesquiera la
cumplen, entonce son equivalentes.
Este modo de enunciar la condición de equivalencia entre dos circuitos nos permite deducir
un método sencillo con el cual poder obtener el valor de un elemento equivalente a un conjunto de elementos que se quieren simplificar, como la resistencia Req del ejemplo que estamos
tratando. El método consta de tres pasos fundamentales:
• Suponer que a ambos circuitos se les aplica una misma tensión entre sus terminales externas, digamos V .
• Supuestas las tensiones de entrada iguales, se obtener las expresiones de las corrientes
de entrada o de salida de ambos circuitos, que serán de la forma Iin (V ) o Iout (V ). En
el circuito equivalente, además, esa expresión contendrá el valor del elemento equivalente
como parámetro. Nótese que éstas expresiones representan la relación existente entre la
tensión que soportan las terminales de los circuitos y sus corrientes de entrada y de salida.
• Como las corrientes de entrada y de salida de ambos circuitos deben ser iguales para que
sean equivalentes, entonces se puede plantear la igualdad Iin1 (V ) = Iin2 (V ), es decir, la
corriente de entrada de uno de los circuitos es igual a la corriente de entrada del otro.
Esta ecuación tiene la peculiaridad de que, al contener el valor del elemento equivalente
como parámetro, y al ser todo lo demás valores conocidos, nos permite despejar de ella el
valor del elemento equivalente buscado.
Existe otro método simétrico que nos permite obtener el valor del elemento equivalente
buscado: se hallan las expresiones la tensión externa (tensión entre los terminales externos) en
ambos circuitos. Esas expresiones serán de la forma V (Iin ) o V (Iout ). Luego se igualan dichas
expresiones, teniendo en cuenta que las corrientes de entrada y de salida en ambos circuitos
deben ser iguales, y finalmente se despeja, de dicha ecuación, el valor del elemento equivalente.
Por ejemplo, en el caso de nuestra resistencia equivalente, basta suponer que al circuito original se le aplica una tensión determinada entre sus terminales, digamos V , obtener la expresión
34
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
+
R1
A
+
A
Iin1
Iin2
R2
V
R3
V
Req
Iout1
Iout2
-
B
R4
B
Figura 4.5: método de obtención de la resistencia equivalente
de la corriente de entrada o de salida (la corriente de entrada tiene el mismo valor que la de
salida, ası́ que da lo mismo), e igualar dicha expresión a la de la corriente de entrada (o de
salida) del circuito equivalente al aplicársele a éste la misma tensión V . Esa ecuación deberı́a
permitirnos despejar el valor del elemento equivalente, en nuestro ejemplo la resistencia Req .
Aplicando el procedimiento antes explicado, tendrı́amos primero que suponer que a cada
circuito se le aplica una diferencia de tensión V , con una polaridad determinada. Dicho proceso
se presenta en la Figura 4.5.
En este caso las polaridades asignadas implican que Va − Vb = V . Obtenidas las expresiones
de Iin o Iout en función de V , es decir, expresiones de la forma Iin1 (V ) o Iout1 (V ), que nos dan
la ecuación que relaciona la tensión en los terminales externos, V , con las corrientes de entrada
y de salida, ası́ como las expresiones de Iin2 (V ) o Iout2 (V ), bastarı́a imponer la condición:
Iin1 (V ) = Iin2 (V )
U otras similares, considerando que las corrientes de entrada son iguales a las de salida en cada
circuito, para obtener la expresión de Req que hace que ambos circuitos sean equivalentes.
Vamos ahora a estudiar los dos tipos de asociaciones que aparecen la mayor parte del tiempo
en circuitos convencionales, las asociaciones en serie y en paralelo.
4.2.
Asociaciones en serie
Se dice que dos o más elementos están conectados en serie si están situados en
la misma rama. Hasta ahı́ llega la definición, ni más, ni menos. Digo esto, porque a lo largo
de mi experiencia he podido constatar que hay gente que, tras haber estado estudiando teorı́a
de circuitos más de un año, no eran capaces de distinguir cuándo habı́a elementos electrónicos
situados en serie. Si los elementos están en la misma rama, están en serie. En cualquier otro
caso, no.
Supongamos el circuito de la Figura 4.6, donde hay un buen montón de elementos electrónicos de los ya explicados. En el circuito, los elementos L1 , C1 , R1 , V y L2 están en serie,
ya que se sitúan sobre la misma rama, la rama A-E-C. Los elementos I2 y C2 también están
en serie, ya que se sitúan sobre la misma rama, la A-D. Por contra, los elementos C1 , L1 e I2
no están en serie, ya que los dos primeros están en la rama A-E-C y el segundo en la rama
A-D. Los elementos I4 y C4 tampoco están en serie, ya que el primero está en la rama A-B y
el segundo en la rama B-C.
En esta sección vamos a analizar qué ocurre cuando se sitúan series de elementos del mismo
tipo conectados en serie (resistencias o condensadores o bobinas o fuentes de tensión o de
corriente, pero no una combinación de ellos), y los elementos equivalentes que los pueden
sustituir.
35
4.2. ASOCIACIONES EN SERIE
C1
A L1
I2
R1
I1
E
C2
B
V
D
R3
C4
C3
R2
C
L2
Figura 4.6: un circuito con varias conexiones en serie
R1
R2
Rn
...
A
B
Figura 4.7: n resistencias conectadas en serie
4.2.1.
Resistencias
Supongamos el conjunto de resistencias asociadas en serie de la Figura 4.7.
Nos preguntamos si existe una resistencia equivalente a todas ellas, es decir, si existe una
resistencia de valor Req (Figura 4.8) tal que, al ponerla entre los puntos A y B en lugar de la
serie de resistencias, el circuito externo a ella muestra el mismo comportamiento que cuando
estaban las resistencias originales.
Para hallar el valor de la resistencia equivalente Req , aplicaremos el método explicado al
principio de este tema, en la sección 4.1.
En primer lugar, vamos a suponer que a ambos circuitos, entre sus terminales A y B se les
aplica una misma tensión V (t), como se muestra en la Figura 4.9.
En estas circunstancias, podemos hallar fácilmente las expresiones de las corrientes de entrada y de salida de ambos circuitos, aplicando las Leyes de Kirchoff explicadas en el capı́tulo
anterior. Los puntos A y B del circuito de la derecha se han renombrado a P1 y Pn+1 , para
facilitar el análisis matemático, si bien siguen siendo los mismos.
Vayamos al circuito de la derecha, el que contiene todas las resistencias sin simplificar. Como
en ese circuito sólo hay una rama, sabemos que la corriente que circula por todos sus puntos es
la misma, es decir, la corriente que atraviesa todas las resistencias es la misma. Llamemos a esa
corriente I(t) (que coincide además con Iin (t) e Iout (t)). Si aplicamos la ley de Ohm a cada una
de las resistencias del circuito, podemos obtener la diferencia de tensión existente entre cada
Req
A
B
Figura 4.8: resistencia equivalente
36
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
Req
A
B
P2
R2
Iin2
Pn
...
Rn
Pn+1
Iout2
+
−
Iout1
R1
+
−
Iin1
P1
V(t)
V(t)
Figura 4.9: método de obtención de la resistencia equivalente
una de ellas. Recuérdese que la corriente que atraviesa a todas las resistencias es la misma, I(t):
VP1 (t) − VP2 (t) = I(t)R1
VP2 (t) − VP3 (t) = I(t)R2
..
.
VPn (t) − VPn+1 (t) = I(t)Rn
Si nos damos cuenta, a excepción de la primera y la última ecuación, en cada ecuación i aparece
un término de tensión Vi (t) que en la ecuación anterior aparece con signo opuesto. Por tanto,
si se suman todas las ecuaciones, se deduce que:
VP1 (t) − VPn+1 (t) = V (t)
= I(t)R1 + IR2 + . . . + IRn
= I(t)(R1 + R2 + . . . + Rn ) ⇒
V (t)
I(t) = Iin1 (t) = Iout1 (t) =
R1 + R2 + . . . + Rn
Donde se ha tenido en cuenta que VP1 (t) − VPn+1 (t) = V (t) según la fuente de tensión, ya que la
diferencia de tensión entre su polo positivo y su polo negativo es igual al valor de la fuente. Esta
es la expresión que relaciona las corrientes de entrada y de salida con la tensión que soportan
los terminales del circuito, tal y como ya se explicó en la sección 4.1.
Si ahora nos centramos en el circuito que contiene a la hipotética resistencia equivalente y
hallamos la relación que existe entre la tensión aplicada a sus terminales y las corrientes de
entrada y de salida, no es difı́cil deducir, aplicado simplemente la Ley de Ohm, que:
VA (t) − VB (t)
Req
V (t)
=
Req
Iin2 (t) = Iout2 (t) =
Sigamos con el procedimiento que explicamos en la sección 4.1. Ambos circuitos se suponen
equivalentes si, al aplicárseles la misma tensión a sus terminales externos, sus corrientes de
entrada y de salida son iguales. La condición de aplicárseles la misma tensión a sus terminales
externos ya ha sido impuesta (dicha tensión está representada por la fuente V (t)). Queda
satisfacer la segunda condición, es decir, imponer que las corrientes de entrada o de salida de
37
4.2. ASOCIACIONES EN SERIE
L1
L2
Ln
...
A
B
Figura 4.10: n bobinas conectadas en serie
Leq
A
B
Figura 4.11: bobina equivalente
ambos circuitos sean iguales. Si imponemos esa condición, se tiene:
Iin1 (t) = Iin2 (t) ⇔
V (t)
V (t)
=
⇔
R1 + R2 + . . . + Rn
Req
1
1
=
⇔
R1 + R2 + . . . + Rn
Req
Req = R1 + R2 + . . . + Rn
(4.1)
¡Eureka! Nuestra primera fórmula que muestra el valor equivalente de una asociación de elementos. Esta fórmula nos dice que la resistencia equivalente a una serie de resistencias
colocadas en serie es igual a la suma de las resistencias. Por tanto, cualquier sucesión de resistencias en serie se podrı́a sustituir por una única resistencia con valor
igual a la suma de las resistencias, según se muestra en la ecuación (4.1).
4.2.2.
Bobinas
Supongamos un conjunto de bobinas conectadas en serie, como muestra la Figura 4.10.
Queremos ver si existe una bobinar equivalente a todas ellas, es decir, si existe una bobina
de valor Leq (Figura 4.11) tal que, si se conecta a las terminales A y B en lugar de la sucesión
de n bobinas, entonces el comportamiento del circuito externo a las terminales A y B sigue
siendo el mismo que con las n bobinas.
Sigamos el procedimiento explicado en la sección 4.1 para obtener el valor de esa inductancia
equivalente Leq .
En primer lugar, apliquemos a cada circuito una misma tensión V (t) entre las terminales A
y B, y obtengamos las corrientes de entrada y de salida para cada circuito (Figura 4.12).
Además, los puntos A y B del circuito de la derecha han sido renombrados a P1 y Pn+1 ,
para facilitar el análisis matemático, si bien siguen siendo los mismos.
El circuito de la derecha contiene una sola rama y también una sola malla. Pensemos en
ramas más que en mallas. Como hay una sola rama, la corriente que circula por todos sus
Leq
A
P1
L1
P2
L2
B
Iin2
Iout2
+
−
Iout1
+
−
Iin1
Pn Ln
...
V(t)
V(t)
Figura 4.12: método de obtención de la bobina equivalente
Pn+1
38
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
puntos es la misma, y ası́ la corriente en cada bobina es la misma que en las demás. Llamemos
a esa corriente I(t), y supongamos que tiene un sentido igual al de las corrientes de entrada y
de salida. Entonces, en cada bobina podemos usar su ecuación caracterı́stica, (2.4), y obtener
las siguientes ecuaciones:
dI(t)
dt
dI(t)
VP2 (t) − VP3 (t) = L2
dt
..
.
VP1 (t) − VP2 (t) = L1
VPn (t) − VPn+1 (t) = Ln
dI(t)
dt
Si ahora sumamos toda esa ristra de ecuaciones entre sı́, al igual que antes, todas las tensiones
a excepción de VP1 (t) y VPn+1 (t) desaparecen:
VP1 (t) − VPn+1 (t) = V (t)
dI(t)
dI(t)
dI(t)
+ L2
+ . . . + Ln
= L1
dt
dt
dt
dIin1 (t)
(L1 + L2 + . . . + Ln )
=
dt
Donde se ha tenido en cuenta que VP1 (t) − VPn+1 (t) = V (t) según la fuente de tensión, ya que
la diferencia de tensión entre su polo positivo y su polo negativo es igual al valor de la fuente.
También se ha renombrado a I(t) como Iin (t), ya que coinciden (al igual que con Iout (t), pero
no se ha escrito ası́). Esta es la expresión que relaciona las corrientes de entrada y de salida con
la tensión que soportan los terminales del circuito, tal y como ya se explicó en la sección 4.1.
En el circuito de la izquierda, el que contiene la hipotética bobina equivalente, la ecuación
que caracteriza su corriente de entrada y de salida es inmediata, y coincide con la propia de
una bobina:
dIin2 (t)
V (t) = Leq
dt
¿Qué hay que hacer ahora para obtener el valor de Leq ? A diferencia de como hemos hecho
hasta ahora al basarnos en igualar las expresiones de las corrientes de entrada o de salida de
cada circuito, en este caso ese método serı́a más complicado, puesto que requerirı́a despejar
Iin (t), para lo cual habrı́a que resolver una integral. Sı́, es muy sencillo de plantear, pero es que
el método de igualar las tensiones aplicadas a los terminales de los circuitos (que también se
nombró al final de la sección 4.1) nos va a ser mucho más fácil en este caso, ası́ que aplicaremos
el procedimiento alternativo de igualar la expresiones de las tensiones externas. Si igualamos
ambos valores de V (t), considerando que las corrientes Iin1 (t) e Iin2 (t) han de ser iguales para
que ambos circuitos sean equivalentes:
dIin1 (t)
dIin2 (t)
(L1 + L2 + . . . + Ln ) = Leq
⇔
dt
dt
Leq = L1 + L2 + . . . + Ln
(4.2)
Es decir, la inductancia equivalente a una serie de bobinas conectadas en serie, es
igual a la suma de las inductancias de cada bobina. Por tanto, una sucesión de
bobinas en serie se puede sustituir por una bobina con valor igual a la suma de
los valores de cada bobina, como se indica en la ecuación (4.2). En este sentido, las
bobinas se comportan igual que las resistencias.
39
4.2. ASOCIACIONES EN SERIE
C1
C2
Cn
...
A
B
Figura 4.13: n condensadores conectados en serie
Ceq
A
B
Figura 4.14: condensador equivalente
4.2.3.
Condensadores
Supongamos un conjunto de condensadores conectados en serie, como muestra la Figura
4.13.
Queremos ver si existe un condensador equivalente a todos ellos, es decir, si existe un
condensador de valor Ceq (Figura 4.14) tal que, si se conecta a las terminales A y B en lugar de
la sucesión de n condensadores, entonces el comportamiento del circuito externo a las terminales
A y B sigue siendo el mismo que con los n condensadores.
Sigamos el procedimiento explicado en la sección 4.1 para obtener el valor de esa capacidad
equivalente Ceq .
En primer lugar, apliquemos a cada circuito una misma tensión V (t) entre los terminales A
y B, y obtengamos las corrientes de entrada y de salida para cada circuito (Figura 4.15).
Además, los puntos A y B del circuito de la derecha han sido renombrados a P1 y Pn+1 ,
para facilitar el análisis matemático, si bien siguen siendo los mismos.
El circuito de la derecha contiene una sola rama y también una sola malla. Pensemos en
ramas más que en mallas. Como hay una sola rama, la corriente que circula por todos sus puntos
es la misma, y ası́ la corriente en cada condensador es la misma que en los demás. Llamemos
a esa corriente I(t), y supongamos que tiene un sentido igual al de las corrientes de entrada
y de salida. Entonces, en cada condensador podemos usar su ecuación caracterı́stica, (2.7), y
obtener las siguientes ecuaciones:
d(VP1 (t) − VP2 (t))
dt
d(VP2 (t) − VP3 (t))
I(t) = C2
dt
..
.
I(t) = C1
I(t) = Cn
d(VPn (t) − VPn+1 (t))
dt
Si en cada ecuación pasamos la capacidad Ci dividiendo al otro miembro de la igualdad, y
Ceq
A
P1
C1
P2
C2
B
Iin2
Cn
Iout2
+
−
Iout1
+
−
Iin1
Pn
...
V(t)
V(t)
Figura 4.15: método de obtención de la capacidad equivalente
Pn+1
40
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
desarrollamos la derivada, tenemos:
I(t)
dVP1 (t) dVP2 (t)
=
−
C1
dt
dt
dVP2 (t) dVP3 (t)
I(t)
=
−
C2
dt
dt
..
.
I(t)
dVPn (t) dVPn+1 (t)
=
−
Cn
dt
dt
Si ahora sumamos toda esa ristra de ecuaciones entre sı́, al igual que antes, hay una serie de
términos que desaparecen, y quedan sólo las tensiones en los puntos P1 y Pn+1 :
I(t)
1
1
1
I(t) I(t)
+
+ ...+
= I(t)
+
+ ...+
C1
C2
Cn
C1 C2
Cn
d(VP1 (t) − VPn+1 (t)
⇒
=
dt
−1
dV (t) 1
1
1
I(t) = Iin1 (t) = Iout1 (t) =
+
+ ...+
dt
C1 C2
Cn
Donde se ha tenido en cuenta que VP1 (t) − VPn+1 (t) = V (t) según la fuente de tensión, ya que la
diferencia de tensión entre su polo positivo y su polo negativo es igual al valor de la fuente. Esta
es la expresión que relaciona las corrientes de entrada y de salida con la tensión que soportan
los terminales del circuito, tal y como ya se explicó en la sección 4.1.
En el circuito de la izquierda, el que contiene la hipotética capacidad equivalente, la ecuación
que caracteriza su corriente de entrada y de salida es inmediata, y coincide con la propia de un
condensador:
dV (t)
Iin2 (t) = Iout2 (t) = Ceq
dt
Si ahora imponemos la condición de que las corrientes de entrada o de salida sean iguales en
ambos circuitos, obtenemos una ecuación de la que obtener el valor de Ceq :
dV (t)
dt
Iin1 (t) = Iin2 (t) ⇔
−1
1
1
1
dV (t)
+
+ ...+
⇔
= Ceq
C1 C2
Cn
dt
1
1
1
1
=
+
+ ...+
Ceq
C1 C2
Cn
(4.3)
Es decir, el inverso de la capacidad equivalente de una serie de condensadores
conectados en serie, es igual a la suma de los inversos de las capacidades de cada
uno de los condensadores. Ası́ pues, cualquier sucesión de condensadores conectados en serie se puede sustituir por un condensador equivalente de capacidad
correspondiente a la mostrada en la ecuación (4.3).
4.2.4.
Fuentes de tensión
La asociación de fuentes, ya sean de tensión o de corriente, son quizás un caso algo especial,
que puede ser atacado de un modo distinto, y más sencillo, al de resolver un circuito complejo.
Debemos pensar que una fuente de tensión no es más que un elemento que fija entre sus
terminales una determinada tensión, independientemente de la corriente que por ella circule.
41
4.2. ASOCIACIONES EN SERIE
P1
P2
Vn(t)
...
P3
B
+
−
+
−
A
V2(t)
+
−
V1(t)
Pn
Pn+1
Figura 4.16: n fuentes de tensión conectadas en serie
A
+
−
Veq(t)=V1(t) +...+ Vn(t)
B
Figura 4.17: fuente de tensión equivalente
La diferencia entre el valor de la tensión en el polo positivo y el polo negativo es igual al valor
de la fuente.
¿Qué es un conjunto de fuentes de tensión conectadas en serie? Una cosa más rara, más
grande, y posiblemente con un pene más luengo, pero que hace lo mismo que una única fuente
de tensión, es decir, imponer una determinada tensión entre los terminales externos de toda
esa serie de fuentes de tensión. Supongamos un conjunto de fuentes de tensión en serie, como
muestra la Figura 4.16.
Ese conjunto de fuentes de tensión serán muy bonitas, muy redondas, muy numerosas, pero
se comportan como una única fuente de tensión cuyo valor de tensión es el que hay entre A y
B. Pensemos un poco: si entre A y B esta serie de fuentes imponen una determinada tensión,
¿no serı́a lo mismo poner una única fuente cuyo valor fuera el que imponen todas esas fuentes
entre A y B? Sı́, en efecto. ¿Cuál es la tensión que hay, pues, entre A y B? Apliquemos un
poco el sentido común. Sabemos que, para cada fuente, la diferencia entre la tensión en su polo
positivo y su polo negativo es igual al valor de la fuente. Si aplicamos este concepto a cada una
de las fuentes, obtenemos el siguiente conjunto de ecuaciones:
VP1 (t) − VP2 (t) = V1 (t)
VP2 (t) − VP3 (t) = V2 (t)
..
.
VPn (t) − VPn+1 (t) = Vn (t)
Con lo cual, si sumamos todas las ecuaciones, deducimos que:
VP1 (t) − VPn+1 (t) = V1 (t) + V2 (t) + . . . + Vn (t)
Y dado que los puntos P1 y Pn+1 coinciden con A y B respectivamente,
Veq (t) = V1 (t) + V2 (t) + . . . + Vn (t)
(4.4)
Es decir, la diferencia de tensión entre A y B es igual a la suma de las tensiones de cada una
de las fuentes de tensión situadas entre A y B. Podrı́amos sustituir por tanto toda la serie de
fuentes de tensión por una equivalente (Figura 4.17) de valor Veq (t) igual a la tensión entre A
y B.
El problema es que no siempre las fuentes de tensión de la que obtener la fuente equivalente
están tan ricamente distribuidas como se planteó inicialmente. Las polaridades podrı́an ser de
lo más variopinto. La Figura 4.18 es un ejemplo más realista de lo que podrı́amos encontrarnos
en un circuito.
42
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
5V
6V
1V
1,4V
0,5V
A
B
Figura 4.18: fuentes de tensión conectadas en serie, ahora no tan bonitas como antes
5V
A
6V
C
1V
D
1,4V
E
0,5V
F
B
Figura 4.19: método de obtención de la fuente de tensión equivalente
En el primer ejemplo las polaridades en todas las fuentes tenı́an la misma orientación: polo
positivo a la izquierda y polo negativo a la derecha. En ese caso, la tensión entre A y B, que
serı́a el valor de nuestra fuente de tensión equivalente, seguı́a la fórmula (4.4). En este nuevo
caso, las polaridades de las fuentes no son las mismas, y por ende no se puede aplicar la fórmula
(4.4). No por ello el problema se hace más complejo. Simplemente hay que obtener, nuevamente,
la tensión entre A y B, que será el valor de la fuente de tensión equivalente. Pensemos un poco
en cómo hallar la tensión que hay entre A y B. Dijimos allá por el primer tema, sección 1.2,
que colocar la toma de tierra en cualquier punto del circuito nos permite conocer las tensiones
en cada uno de los puntos del circuito, y sin variar las diferencias de tensión entre cualesquiera
puntos del circuito (que eran lo que realmente tenı́an sentido fı́sico). Si queremos entonces
hallar la diferencia de tensión entre A y B, podrı́amos colocar la tierra en alguno de esos dos
puntos, hallar la tensión en el otro, y después obtener la diferencia. Por ejemplo, supongamos
que colocamos la toma de tierra en A (Figura 4.19).
Colocada la toma de tierra en A, hallemos cuál es la tensión en B. Repetimos que, al colocar
a toma de tierra en un punto cualquiera, las diferencias de tensión entre cualesquiera puntos
del circuito no varı́an, de modo que la diferencia de tensión entre el punto A y el punto B
será la misma que en el circuito sin toma de tierra (de hecho se deja como ejercicio al lector
que pruebe a colocar la tierra en otro punto cualquiera, que halle el valor de la tensión en A y
en B, y que compruebe que la diferencia de tensión es la misma que obtendremos aquı́). Como
la tierra está cortocircuitada con A, se cumple que VA = 0.
Tomando la fuente de 5V , tenemos que VA − VC = 5V ⇒ VC = −5V . La fuente de 6V dice
que VD − VC = 6V ⇒ VD = 1V . La fuente de 1V dice que VE − VD = 1V ⇒ VE = 2V . La
fuente de 1,4V impone la condición VE − VF = 1,4V ⇒ VF = 0,6V . Por último, la fuente de
0,5V nos dice que VB − VF = 0,5V ⇒ VB = 1,1V .
Hemos encontrado pues el valor de VB , que es 1,1V . Como el valor de VA es 0V , se deduce
que la diferencia de tensión entre el punto A y el punto B es:
VAB = VA − VB = 0 − 1,1 = −1,1V
Tenemos que la tensión entre A y B es de −1,1V . Por tanto, la hipotética fuente de tensión
equivalente que deberı́a colocarse entre los terminales A y B debe ser una fuente que haga cierta
la igualdad VAB = VA − VB = 0 − 1,1 = −1,1V . Con respecto a esto, hay varias posibilidades.
Buscamos una fuente que haya que la diferencia de tensión entre A y B sea de −1,1V . Una
posibilidad serı́a la fuente de la Figura 4.20, ya que, según esta fuente, la diferencia de tensión
entre su polo positivo (A) y su polo negativo (B) es −1,1V , que es justamente la condición
VAB = VA − VB = 0 − 1,1 = −1,1V que imponı́a la serie de fuentes de tensión original.
43
4.2. ASOCIACIONES EN SERIE
-1,1V
A
B
Figura 4.20: una de las posibles fuentes de tensión equivalentes
1,1V
A
B
Figura 4.21: la otra posible fuente de tensión equivalente
Ahora bien, hay otra fuente de tensión que ofrece el mismo comportamiento. ¿Cuál? Pues
muy fácil, la de la Figura 4.21.
Esta fuente de tensión impone que la diferencia de tensión entre su polo positivo y su polo
negativo es igual al valor de la fuente, es decir, VB − VA = 1,1V . Si nos damos cuenta, esta
condición es exactamente igual a la que debı́a de cumplir la fuente de tensión equivalente, es
decir, VB − VA = 1,1V ⇒ −(VB − VA ) = −1,1V ⇒ VA − VB = −1,1V , y por tanto esta fuente
también cumple que la tensión que impone entre A y B es igual a la tensión que imponen las
fuentes originales.
Vemos pues que obtener la expresión de la fuente tensión equivalente a una serie de fuentes
de tensión asociadas en serie no es un gran problema: basta hallar la tensión que impone toda
la serie de fuentes en sus extremos. Obtenida ese valor de tensión, habrá que tener en cuenta
que la fuente de tensión equivalente ha de ser tal que la diferencia de tensión entre sus extremos
sea igual a la obtenida del circuito original. A este respecto, hemos visto que hay dos posibles
fuentes equivalentes, que se diferencian en que tienen la polaridad invertida y sus valores tienen
signos opuestos. ¿Por qué esto es ası́? Si existe un elemento equivalente, realmente deberı́a
existir sólo uno, ¿no? La respuesta es que sı́: existe sólo uno. Y a pesar de ello también es cierto
que las fuentes de tensión antes representadas eran equivalentes, pues realmente imponı́an la
misma diferencia de tensión entre sus terminales. Es por ello que se puede considerar que ambas
eran realmente, la misma fuente de tensión.
De forma más general, dada una fuente de tensión genérica como la de la Figura 4.22, dicha
fuente puede ser sustituida por una fuente equivalente como la de la Figura 4.23.
Es decir, a cualquier fuente se le puede invertir la polaridad, y cambiar el signo de su
tensión sin que el resto del circuito aprecie la diferencia. La explicación es muy sencilla. La
fuente original, la de arriba, impone la ecuación VA (t) − VB (t) = V (t); por otro lado, la de
abajo impone VB (t) − VA (t) = −V (t). Aunque parezcan ecuaciones distintas, son realmente la
misma ecuación, y basta trabajar un poco la segunda para llegar a la conclusión de que es la
A
+
−
V(t)
B
Figura 4.22: fuente de tensión genérica
44
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
-V(t)
+
−
A
B
Figura 4.23: fuente de tensión equivalente
I1(t)
A
I2(t)
In(t)
...
B
Figura 4.24: n fuentes de corriente conectadas en serie
misma que la primera. En efecto,
VB (t) − VA (t) = −V (t) ⇔
−(VB (t) − VA (t)) = −(−V (t)) ⇔
VA (t) − VB (t) = V (t)
Y por tanto la segunda fuente de tensión impone entre las terminales A y B la misma tensión
que la fuente original, lo cual las hace a ambas equivalentes. Es precisamente por esto que
en el ejemplo anterior habı́a dos posibles fuentes de tensión equivalentes, porque las dos eran
realmente, a su vez, equivalentes entre sı́ (una era igual a la otra, con la polaridad cambiada y
con el signo de la tensión invertido).
4.2.5.
Fuentes de corriente
Una fuente de corriente, tal y como se explicó en la sección 2.5 no es más que un elemento
electrónico que hace que por ella circule una determinada corriente de valor igual al valor de la
fuente, con el sentido indicado por la flecha de la fuente, y que es independiente de la tensión
que soporta entre sus terminales.
Es importante notar que, dado que en todos los puntos de una rama de un
circuito circula la misma corriente, entonces toda fuente de corriente hace que por
la rama en que se sitúa circule una corriente igual a la que genera la fuente en sı́.
Ahora supongamos que tenemos una serie de fuentes de corriente conectadas en serie (sobre
una misma rama) como muestra la Figura 4.24. Podrı́amos preguntarnos si existe una fuente
de corriente equivalente a todas ellas, una que, situada entre las terminales A y B, juegue el
mismo papel que todas las fuentes iniciales. Podrı́amos, en efecto, preguntarnos esa cuestión.
La pregunta es si, en efecto, esa cuestión tiene sentido.
Pensemos un poco acerca de la asociación de fuentes de corriente en serie. Por definición,
si las fuentes están conectadas en serie, están situadas en la misma rama. Ahora bien, si todas
ellas están en la misma rama, ¿cuál es la corriente que hay en dicha rama? Sabemos que, por
definición, una fuente de corriente impone en toda la rama en la que se sitúa una corriente
determinada igual al su valor de corriente. ¿Qué ocurre en este caso? Que hay varias fuentes de
corriente en la misma rama, por tanto, todas ellas están intentando imponer en la misma rama
su corriente propia. La primera fuente de la figura de arriba intentarı́a imponer una corriente
en la rama A-B que circulase hacia la izquierda, y con un valor I1 (t). Esa corriente deberı́a ser
la que también circulase por las otras fuentes, ya que están en la misma rama que la primera
fuente. Pero por otro lado, la segunda fuente intenta imponer en la rama A-B otra corriente,
hacia la izquierda, y de valor I2 (t). Lo mismo ocurre con todas las demás fuentes de corriente:
cada una intenta imponer en la rama una corriente distinta a la de las otras fuentes, entrando
en conflicto con ellas. ¿El resultado?: Fuego, dolor, explosiones y, sobre todo, suspensos todos.
45
4.3. ASOCIACIONES EN PARALELO
C1
C2
A
+
V1 −
L1
C
R1
C3
R2
B
L2
+
V2 −
L3
D
C4
Figura 4.25: circuito con diversas conexiones en paralelo
Llegamos pues a la conclusión de que no se pueden poner fuentes de corriente en la misma
rama, y por tanto no pueden asociarse en serie.
En la vida real, si en un circuito se colocasen fuentes de corriente en serie, yo me alejarı́a lo
más rápidamente posible, y saltarı́a por la ventana más próxima. Posiblemente alguna fuente
se quemarı́a.
4.3.
Asociaciones en paralelo
Se dice que dos o más elementos electrónicos están conectados en paralelo si
sus dos terminales externas están conectadas, una a una (cortocircuitadas, o son
la misma).
Por ejemplo, supongamos el circuito de la Figura 4.25.
Seamos más cuidadosos en este ejemplo. Generalmente, es más complicado determinar
qué elementos están conectados en paralelo que determinar cuáles están en serie.
Según nuestra definición, todos los elementos que tengan sus terminales conectadas (cortocircuitadas), una a una, estarán conectados en paralelo. La fuente de tensión V2 y el condensador
C4 están conectados en paralelo, ya que por un lado, una de las terminales de la fuente está cortocircuitada con una de las terminales del condensador, y se juntan en el punto D, y la otra
terminal de la fuente también está cortocircuitada con la otra terminal del condensador (ambas
están cortocircuitadas, por ejemplo, con el punto C, y por ende están cortocircuitadas entre sı́).
Los condensadores C1 y C2 también están conectados en paralelo, ya que las terminales derechas
de ambos condensadores están cortocircuitadas en el punto C, y las terminales izquierdas están
también cortocircuitadas (ambas, por ejemplo, se juntan en el punto llamado A y por tanto
están cortocircuitadas). Por último, la fuente V1 , la bobina L1 y la resistencia R1 también están
conectadas en paralelo: las terminales de arriba de cada elemento se cortocircuitan en el punto
A, y las de abajo en el punto B. Todos los demás elementos del circuito no están conectados en
paralelo. Por ejemplo, R1 y R2 no están conectadas en paralelo: si bien tienen dos terminales
cortocircuitados, los que su vez cortocircuitan con el punto B, los otros dos terminales no lo
están: uno conecta con el punto C, y el de la otra resistencia con el punto A. No hay ningún
cortocircuito que conecte ambos terminales, ya que lo impiden los demás elementos del circuito.
Por tanto, R1 y R2 no están conectadas en paralelo.
En esta sección estudiaremos qué ocurre cuando se sitúan series de elementos del mismo
tipo conectados en paralelo (resistencias o condensadores o bobinas o fuentes de tensión o
46
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
R1
R2
..
.
Rn
A
B
Figura 4.26: n resistencias conectadas en paralelo
Req
A
B
Figura 4.27: resistencia equivalente
de corriente, pero no una combinación de ellos), y los elementos equivalentes que los pueden
sustituir.
4.3.1.
Resistencias
Supongamos un conjunto de resistencias conectadas en paralelo (Figura 4.26).
En este circuito tenemos una sucesión de n resistencias cuyos terminales están cortocircuitados con los puntos A y B. Queremos obtener una resistencia equivalente a todas ellas (Figura
4.27), tal que, si se sustituye el conjunto de resistencias original por esa resistencia equivalente,
entonces el circuito externo a las terminales A y B muestre el mismo comportamiento que con
todas las resistencias.
Para obtener el valor de la resistencia equivalente, Req , aplicaremos el procedimiento explicado en la sección 4.1.
Supongamos que a ambos circuitos aplicamos una misma tensión V (t), y analicemos cuál es
la ecuación que relaciona las corrientes de entrada y de salida de ambos circuitos con la tensión
V (t) (Figura 4.28).
Para resolver el circuito de la izquierda vamos a redibujarlo. Sı́, tal y como se comentó en
R1
R2
..
.
Iout1
V(t)
A
B
Iin2
Iout2
B
+
−
A
Rn
+
−
Iin1
Req
V(t)
Figura 4.28: método de obtención de la resistencia equivalente
47
4.3. ASOCIACIONES EN PARALELO
R1
I2 R
2
In
Iin1
..
.
B
Req
Rn I
out1
A
Iin2
Iout2
+
−
A
+
−
I1
V(t)
V(t)
B
Figura 4.29: circuito de la Figura 4.28, redibujado
la sección 3.1, cuando se explicó el concepto de nodo, uno puede modificar la geometrı́a de las
conexiones entre los elementos del circuito siempre que, tras ello, las conexiones se mantengan
inalteradas. En el circuito de la derecha hay que tener en cuenta pues que todos los terminales
izquierdos de las resistencias están conectados (cortocircuitados) entre sı́, ası́ como los terminales
derechos también lo están. Por tanto, si se redibujase el circuito manteniendo esas conexiones,
esos cortocircuitos, el circuito obtenido mostrarı́a el mismo comportamiento. Ası́ pues, podemos
redibujarlo como aparece en la Figura 4.29.
Donde se aprecia que el circuito de la izquierda ha sido redibujado de modo que las
conexiones del circuito original se mantienen inalteradas. El haberlo redibujado ası́ nos permitirá analizar el circuito más fácilmente, si bien sobre el circuito original se puede llevar a
cabo un análisis similar al siguiente y por tanto llegar a la misma expresión para Req .
En el circuito de la izquierda podemos aplicar la ley de los nudos al nudo A. Se ha supuesto
que las corrientes entrantes y salientes del nudo son las de la figura, si bien suponer otras habrı́a
supuesto llegar al mismo resultado. La ley de los nudos nos dice que la suma de las corrientes
que entran al nudo es igual a la suma de las que salen. Como sólo entra una corriente, Iin1 (t),
y las demás salen, la ecuación del nudo A es:
Iin1 (t) = I1 (t) + I2 (t) + . . . + In (t)
Si aplicamos la Ley de Ohm a cada corriente, tenemos:
Iin1 (t) =
VA (t) − VB (t) VA (t) − VB (t)
VA (t) − VB (t)
+
+ ...+
R1
R2
Rn
Y como VA (t) − VB (t) = V (t) (ecuación de la fuente de tensión), entonces:
Iin1 (t) = Iout (t) =
V (t) V (t)
V (t)
+
+ ...+
R1
R2
Rn
Por otro lado, en el circuito equivalente la expresión de la corriente es inmediata y está dada
por la Ley de Ohm:
VA (t) − VB (t)
Req
V (t)
=
Req
Iin2 (t) = Iout2 (t) =
48
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
L1
L2
..
.
A
Ln
B
Figura 4.30: n bobinas conectadas en paralelo
Leq
A
B
Figura 4.31: bobina equivalente
Obtenidas las expresiones de las corrientes de entrada y de salida a cada circuito, para hacer
que sean equivalentes hay que imponer la condición de que las expresiones que relacionan sus
corrientes de entrada o de salida en función de la tensión aplicada a sus terminales externos
(V (t)) sean iguales cuando la tensión aplicada es la misma. Como la tensión aplicada ha sido la
misma en ambos circuitos, resta igualar las expresiones de las corrientes de entrada o de salida
(o las expresiones de V (t)) de ambos circuitos. Se obtiene:
Iin1 (t) = Iin2 (t) ⇔
V (t)
V (t)
V (t) V (t)
+
+ ...+
=
⇔
R1
R2
Rn
Req
1
V (t) V (t)
V (t)
=
+
+ ...+
Req
R1
R2
Rn
(4.5)
Es decir, la el inverso de la resistencia equivalente a una serie de resistencias asociadas en paralelo es igual a la suma de los inversos de los valores de cada una de
las resistencias que están en paralelo. Por tanto, cualquier conjunto de resistencias
conectadas en paralelo se puede sustituir por una resistencia equivalente de valor
dado por la ecuación (4.5).
4.3.2.
Bobinas
Supongamos que tenemos el conjunto de bobinas conectadas en paralelo de la Figura 4.30.
Nuestro objetivo es obtener una bobina equivalente (Figura 4.31), tal que, si se coloca entre
los terminales externos A y B sustituyendo a las n bobinas, entonces el comportamiento del
resto del circuito externo a los terminales A y B es el mismo que el mostrado en el circuito con
las n bobinas.
Para obtener el valor de la bobina equivalente Leq vamos a aplicar el procedimiento explicado
en la sección 4.1: imponer que ambos circuitos sean equivalentes, lo cual significa que, si se les
aplica la misma tensión entre sus terminales externos A y B, entonces las expresiones que
relacionan sus corrientes de entrada y de salida con el voltaje aplicado entre A y B deben ser
iguales. Supongamos que a ambos circuitos se les aplica el mismo voltaje V (t) entre A y B
(Figura 4.32). Esperemos que el circuito de la izquierda no resulte traumático. A diferencia
de lo que hicimos en la sección 4.3.1 y de lo que haremos en la sección 4.3.3, en esta ocasión
49
4.3. ASOCIACIONES EN PARALELO
A Iin1
+
V(t) −
n
In’
n-1
In-1’
n-2
2
In-2’
I3’
I2’
...
I2
In
In-1
In-2
Ln
Ln-1
Ln-2
...
L2
1
I1
L1
B Iout1
A
Iin2
+
V(t) −
Leq
Iout2
B
Figura 4.32: método de obtención de la bobina equivalente, ahora, más complicado
no vamos a redibujar el circuito que contiene los elementos conectados en paralelo. Con ello
pretendemos demostrar que lo que hicimos antes, redibujar los circuitos para obtener más
fácilmente el valor del elemento equivalente, no era ninguna triquiñuela sucia, sino que era
realmente un procedimiento válido.
Entendamos en primer lugar lo que tenemos entre manos. En el circuito de la izquierda
se han señalado n nodos crı́ticos, numerados como n, n − 1, ..., 2, 1. La corriente que circula
por cada bobina Li se ha denominado Ii (t). Cuando la corriente Iin (t) llega al nodo n, ésta
se bifurca en otras dos (los sentidos de circulación los hemos supuesto nosotros, tal y como ya
hemos explicado varias veces). Una de las corrientes en las que se bifurca es In (t), pues es la
que circula por la bobina Ln . La otra corriente en la que se bifurca es la corriente In′ (t). De este
modo, para el nodo n podemos escribir:
Iin1 (t) = In (t) + In′ (t)
(Nodo n)
En el nodo n − 1 ocurre más de lo mismo: la corriente In′ (t) se bifurca en otras dos, y según la
ley de los nudos podremos escribir:
′
In′ (t) = In−1 (t) + In−1
(t)
(Nodo n-1)
Para el nodo n − 2 se podrı́a escribir:
′
′
In−1
(t) = In−2 (t) + In−2
(t)
(Nodo n-2)
En general, exceptuando el nodo n y el nodo 1, para cualquier nodo i se cumple que:
′
Ii+1
(t) = Ii (t) + Ii′ (t)
(4.6)
En el nodo número 1 se cumple:
I2′ (t) = I1 (t)
Ya que las corrientes I2′ (t) e I1 (t) circulan realmente por la misma rama. Ahora pensemos un
poco. Si consideramos que I2′ (t) = I1 (t), en la ecuación del nodo 2 podrı́amos escribir:
I3′ (t) = I2 (t) + I2′ (t)
= I2 (t) + I1 (t)
Pero es que, obtenido el valor de I3′ (t), se puede reescribir la ecuación del nudo 3 del siguiente
modo:
I4′ (t) = I3 (t) + I3′ (t)
= I3 (t) + I2 (t) + I1 (t)
50
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
Ahora el valor de I4′ (t) lo podrı́amos usar para reescribir la ecuación del nudo 4, y obtener que:
I5′ (t) = I4 (t) + I4′ (t)
= I4 (t) + I3 (t) + I2 (t) + I1 (t)
Y ası́ sucesivamente, llegando finalmente a la conclusión de que, en el nodo n, se cumple que:
Iin1 (t) = In (t) + In−1 (t) + . . . + I1 (t)
Sabemos además que la ecuación de cada bobina nos dice que:
VA (t) − VB (t) = V (t)
dIi (t)
(i=1,. . . ,n)
= Li
dt
Donde se ha considerado que, según la fuente de tensión, VA (t) − VB (t) = V (t). Si pasamos las
inductancias al miembro izquierdo de la ecuación:
dIi (t)
V (t)
=
(i=1,. . . ,n)
Li
dt
Si sumamos el conjunto de ecuaciones definidos por la expresión anterior, y usamos la ecuación
del nudo n:
V (t) V (t)
V (t)
dI1 (t) dI2 (t)
dIn (t)
+
+ ...+
=
+
+ ...+
⇔
L1
L2
Ln
dt
dt
dt
1
1
1
d(I1 (t) + I2 (t) + . . . + In (t))
V (t)
+
+ ...+
+ =
⇔
L1 L2
Ln
dt
1
1
dIin1 (t)
1
+
+ ...+
+ =
⇔
V (t)
L1 L2
Ln
dt
−1
1
1
dIin1 (t) 1
+
+ ...+
+
V (t) =
dt
L1 L2
Ln
Ya tenemos, al fin, la expresión que relaciona la tensión externa y la corriente de entrada (o de
salida) del circuito con las bobinas asociadas en paralelo. Obtener la expresión del circuito de
la derecha, el del modelo equivalente, es inmediato:
VA (t) − VB (t) = V (t)
dIin2 (t)
= Leq
dt
Para que ambos circuitos sean equivalentes, las expresiones que relacionan la tensión externa
aplicada, V (t), con las corrientes de entrada y de salida, han de ser iguales en ambos circuitos.
Por tanto, basta ahora igualar las expresiones de V (t) en ambos circuitos para obtener el valor de
Leq , considerando que Iin1 e Iin2 han de ser iguales para que ambos circuitos sean equivalentes:
−1
1
1
dIin2 (t)
dIin1 (t) 1
+
+ ...+
⇔
= Leq
dt
L1 L2
Ln
dt
−1
1
1
1
+
+ ...+
⇔
Leq =
L1 L2
Ln
1
1
1
1
=
+
+ ...+
(4.7)
Leq
L1 L2
Ln
Es decir, la el inverso de la inductancia equivalente a una serie de bobinas asociadas
en paralelo es igual a la suma de los inversos de los valores de cada una de las
bobinas que están en paralelo. Por tanto, cualquier conjunto de bobinas conectadas
en paralelo se puede sustituir por una bobina equivalente de valor dado por la
ecuación (4.7).
51
4.3. ASOCIACIONES EN PARALELO
C1
C2
.
Cn ..
A
B
Figura 4.33: n condensadores conectados en paralelo
Ceq
A
B
Figura 4.34: condensador equivalente
4.3.3.
Condensadores
Supongamos una serie de condensadores conectados en paralelo tal y como muestra la Figura
4.33.
Los n condensadores están conectados de forma directa a los terminales externos, A y B.
El objetivo es encontrar un condensador equivalente (Figura 4.34) a todos ellos de modo que,
si se sustituye todo el conjunto de condensadores entre A y B por ese condensador equivalente,
entonces el circuito externo a A y B se comporte de la misma manera que con el conjunto de
condensadores.
Al igual que hicimos en la sección 4.3.1, redibujaremos el conjunto de condensadores asociados en paralelo para que sea más fácil el análisis del circuito. Basta retorcer las terminales
de los condensadores manteniendo los mismos puntos de contacto que en el circuito original, lo
cual viene a significar que todos los terminales derechos sigan cortocircuitados, que todos los
terminales izquierdos sigan cortocircuitados, y que no se cree ninguna nueva conexión (Figura
4.35).
Apliquemos ahora el procedimiento explicado en la sección 4.1. para obtener el valor de la
capacidad equivalente, Ceq .
C1
C2
.
Cn ..
A
B
Figura 4.35: los n condensadores en paralelo, redibujados
52
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
C1
I2 C2
.
Cn ..
In
A
Iout1
Iin2
B
+
−
Iin1
Ceq
A
V(t)
Iout2
+
−
I1
B
V(t)
Figura 4.36: método de obtención de la capacidad equivalente
Supongamos ahora que a ambos circuitos (el del condensador equivalente y el de los condensadores en paralelo) se les aplica una misma tensión entre sus terminales A y B, digamos
V (t), y analicemos cuál es la ecuación que relaciona la tensión V (t) y las corrientes de entrada
y de salida en ambos circuitos (Figura 4.36).
En el circuito de la izquierda podemos aplicar la ley de los nudos al nudo que cortocircuita
con el nodo A, aquél al que entra Iin1 (t) y del que salen I1 (t),I2 (t), . . . ,In (t). La ley de los nudos
nos dice:
Iin1 (t) = I1 (t) + I2 (t) + . . . + In (t)
Si consideramos que cada corriente Ii (t) se puede obtener según la ecuación del condensador
por el que circula, tenemos:
dV (t)
d(VA (t) − VB (t))
= C1
dt
dt
dV (t)
d(VA (t) − VB (t))
= C2
I2 (t) = C2
dt
dt
..
.
I1 (t) = C1
In (t) = Cn
dV (t)
d(VA (t) − VB (t))
= Cn
dt
dt
Donde se ha considerado que VA (t) − VB (t) = V (t) según la fuente de tensión. Si sumamos
todas las ecuaciones anteriores, se tiene:
I1 (t) + I2 (t) + . . . + In (t) = C1
dV (t)
dV (t)
dV (t)
+ C2
+ . . . + Cn
dt
dt
dt
Y considerando que la ecuación del nudo:
Iin1 (t) = Iout (t) = C1
dV (t)
dV (t)
dV (t)
+ C2
+ . . . + Cn
dt
dt
dt
Por otro lado, en el circuito de la derecha, la corriente de entrada (o de salida) se puede hallar
directamente mediante la ecuación del condensador:
d(VA (t) − VB (t))
dt
dV (t)
= Ceq
dt
Iin2 (t) = Iout2 (t) = Ceq
53
4.3. ASOCIACIONES EN PARALELO
A
+
+
+
V1(t) − V2(t) − . . . Vn(t) −
B
Figura 4.37: n fuentes de tensión conectadas en serie
Como queremos que ambos circuitos sean equivalentes, las expresiones de las corrientes de
entrada o de salida de ambos circuitos ante tensiones iguales en las terminales A y B deben ser
iguales. La tensión ha sido supuesta la misma, y por tanto sólo queda imponer la condición de
que ambas corrientes sean iguales. De esa ecuación se deduce el valor de la capacidad equivalente:
Iin1 (t) = Iin2 (t) ⇔
dV (t)
dV (t)
dV (t)
dV (t)
C1
+ C2
+ . . . + Cn
= Ceq
⇔
dt
dt
dt
dt
Ceq = C1 + C2 + . . . + Cn
(4.8)
Es decir, la capacidad equivalente de una serie de condensadores asociados en
paralelo es igual a la suma de las capacidades de cada uno de los condensadores.
Por tanto, cualquier conjunto de condensadores conectados en paralelo pueden
sustituirse por un único condensador cuya capacidad es igual a la suma de las
capacidades de los condensadores, tal y como indica la ecuación (4.8).
4.3.4.
Fuentes de tensión
Supongamos que tenemos un conjunto de fuentes de tensión asociadas en paralelo, como
muestra la Figura 4.37.
Queremos comprobar si existe una determinada fuente de tensión que, colocada entre los
terminales A y B en sustitución de las n fuentes, muestre el mismo comportamiento que las n
fuentes juntas.
El problema de la asociación de fuentes de tensión en paralelo es igual al de la asociación
de fuentes de corriente en serie, en el sentido de que es algo que no tiene sentido, y no deberı́a
darse en ningún circuito bajo pena de que arda por completo.
Es fácil ver que no es posible asociar fuentes de tensión en paralelo. Pensemos un poco.
Fijémonos en la fuente de tensión V (t). Esa fuente, tal y como está dibujada, impone la ecuación
VA (t) − VB (t) = V1 (t). Por otro lado, la segunda fuente de tensión, V2 (t), impone la ecuación
VA (t) − VB (t) = V2 (t). En general, cada fuente de tensión está imponiendo entre el punto A y
el punto B una determinada diferencia de tensión. ¿Cuál es la tensión que, entonces, hay entre
los puntos A y B? Mejor no pensarlo: todas las fuentes intentarán imponer su tensión, con
consecuencias presumiblemente catastróficas para el circuito, motivo por el cual no es posible
asociar fuentes de tensión en paralelo.
54
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
A
I1(t)
. . . I (t)
n
I2(t)
B
Figura 4.38: n fuentes de corriente conectadas en paralelo
A
Iout(t)
C
I1(t)
In(t)
I2(t)
I1(t)
I2(t)
. . . I (t)
n
Iin(t)
B
Figura 4.39: las n fuentes de corriente en paralelo, redibujadas
4.3.5.
Fuentes de corriente
Supongamos un conjunto de fuentes de corriente conectadas en paralelo, tal y como muestra
la Figura 4.38.
Queremos ver si existe una determinara fuente de corriente equivalente a todas ellas, es
decir, una fuente de corriente que, colocada entre los terminales A y B, haga el mismo trabajo
que las n fuentes en paralelo, de tal modo que el circuito externo a todas ellas no vea modificado
su comportamiento.
A diferencia de las fuentes de tensión, las fuentes de corriente sı́ se pueden asociar en paralelo.
El conjunto de fuentes en paralelo, a efectos prácticos, lo único que hace es generar una corriente
de entrada y de salida por los terminales A y B. Esa corriente puede ser fácilmente hallada
mediante la ley de los nudos. Si redibujamos el circuito original de una forma equivalente (Figura
4.39), podremos hallar fácilmente cuál es la corriente de entrada y de salida que el conjunto de
fuentes impone a las terminales A y B.
Si aplicamos la ley de los nudos al nudo C, podemos obtener la expresión de la corriente
Iout (t), y que coincide con Iin (t):
Iout (t) = I1 (t) + I2 (t) + . . . + In (t)
(4.9)
Ya que, según los sentidos supuesto para cada corriente, la única que sale es Iout (t), mientras
que todas las demás entran. La corriente Iout (t) es igual que la corriente Iin (t), y por tanto
55
4.3. ASOCIACIONES EN PARALELO
A
Ieq(t)=I1(t)+I2(t)+...+In(t)
B
Figura 4.40: fuente de corriente equivalente
A
Iout
C
2mA
4mA
5mA
3mA
2mA
3mA
5mA
D
4mA
Iin
B
Figura 4.41: un conjunto de fuentes de corriente en paralelo, más terrenal
se puede decir que lo único que hacen todas las fuentes en paralelo no es más que imponer
una corriente entre los puntos A y B, a saber, Iout (t) o Iin (t). Por tanto, todo ese conjunto de
fuentes se podrı́a sustituir por una única fuente que inyectase corriente de A a B, y con el valor
equivalente hallado (Figura 4.40).
El problema de la fórmula (4.9), al igual que ocurrı́a con la asociación de fuentes de tensión en
paralelo, radica en que no siempre las fuentes de corriente están tan exquisitamente colocadas,
orientadas todas en un mismo sentido. Supongamos un conjunto de fuentes más mundano, como
el de la Figura 4.41.
Las corrientes que circulan por cada una de las ramas que conectan los nodos C y D están
determinadas por las fuentes de corriente. Si aplicamos la ley de los nudos al nudo C, suponiendo
que la corriente que circula por la rama C-A tiene el sentido dibujado (Iout ), entonces la ecuación
que se obtiene es:
2 · 10−3 + 3 · 10−3 + 4 · 10−3 + Iout = 5 · 10−3
Ya que la única corriente que entra al nudo es es la de 5mA. De la ecuación se puede deducir
el valor de Iout :
Iout = −4mA
¿Qué es esto? ¿Una corriente negativa? ¿Dónde está Wally? Nos hemos encontrado con algo que
no nos esperábamos. Hasta ahora sólo habı́amos visto corrientes positivas, pero ahora parece que
también existen corrientes negativas. ¿Qué es una corriente negativa? Una corriente negativa
56
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
A
-4mA
B
Figura 4.42: fuente de corriente equivalente
A
I(t)
B
Figura 4.43: una fuente de corriente
no es más que una corriente negativa. Punto y final. Bueno, lo cierto es que si sólo tuviera que
decir esto de las corrientes negativas, no estarı́a haciendo tanto el capullo, ası́ que entremos en
el meollo de la cuestión.
Hemos deducido que las corrientes Iin e Iout son corrientes de valor negativo. Como esas
corrientes circulan entrando a través de B y saliendo desde A, entonces la fuente de corriente
equivalente que podrı́a sustituir al conjunto de fuentes en paralelo es la representada en la
Figura 4.42.
Ya que el conjunto de fuentes inicial hacı́a exactamente eso, inyectar una corriente desde el
punto B al punto A de −4mA.
Sin embargo, volviendo al tema de la corriente de valor negativo, de nuevo surge la pregunta:
¿qué significa? Las corrientes de valor negativo son algo común en teorı́a de circuitos. De hecho,
con el paso del tiempo, nos familiarizaremos de tal modo que nos resulten iguales a las corrientes
de valor positivo. Es más, no es que nos acabarán resultando iguales; es que, de hecho, en cierto
modo, son equivalentes. Uf, respirar, respirar, respirar. Esto puede que nos resulte impactante.
Que las corrientes positivas sean equivalentes, de algún modo, a las corrientes negativas,
significa que para toda corriente negativa existe una corriente positiva, y equivalente, que la
puede sustituir. Esto es parecido a lo que ocurrı́a con las fuentes de tensión. En la sección 4.2.4,
donde explicábamos la asociación de fuentes de tensión en serie, se demostró que toda fuente
de tensión se podı́a sustituir por una fuente con la polaridad cambiada y de valor de tensión
opuesto (cambiado de signo). Con las fuentes de corriente ocurre algo similar: toda fuente
de corriente de valor I(t) se puede sustituir por otra fuente de valor −I(t) y con el
sentido de circulación opuesto.
Dicho de otro modo, una fuente de corriente genérica, como la de la Figura 4.43, se puede
sustituir por otra equivalente, como la de la Figura 4.44.
Explicado el qué, restarı́a explicar el por qué. Pensemos un poco más acerca de la ley de los
nudos. En general, dijimos que en un circuito se podı́a suponer que cada corriente del circuito
circulaba con un sentido impuesto por nosotros de forma totalmente arbitraria. Aunque se
pueda hacer, es lógico que, a la hora de resolver un circuito, haya diferencias si se suponen unos
sentidos u otros. Fijémonos en el ejemplo de la asociación de fuentes de corriente en paralelo.
Si hubiéramos supuesto que la corriente Iout tenı́a un sentido de circulación opuesto al que
57
4.4. MÁS ACERCA DE ASOCIACIONES
A
-I(t)
B
Figura 4.44: la fuente de corriente equivalente
A
4mA
B
Figura 4.45: la otra fuente de corriente equivalente
pensamos, entonces se habrı́a obtenido la siguiente ecuación en el nudo C:
2 · 10−3 + 3 · 10−3 + 4 · 10−3 = 5 · 10−3 + Iout ⇔ Iout = 4mA
Es decir, ¡la corriente Iout habrı́a sido igual, pero de signo opuesto! Si consideramos esta nueva
situación, la fuente de corriente que habrı́a sustituido al conjunto de fuentes en serie habrı́a
sido la fuente representada en la Figura 4.45, donde el sentido está opuesto al de antes dado
que las corrientes Iout e Iin supuestas ahora tenı́an el sentido entrando por A y saliendo desde
B. Pero si nos fijamos, esta es una fuente de corriente justamente equivalente a la original,
que apuntaba de B a A y de valor −4mA, ya que, como hemos dicho, ambas tienen sentidos
opuestos y el mismo valor pero con signo cambiado.
La conclusión que se puede extrapolar de este pequeño ejemplo, es que cuando en un circuito se suponen sentidos arbitrarios para las corrientes, el resultado de las corrientes que se
obtienen no se ven alterados. Simplemente, si un circuito se resuelve suponiendo que
una corriente circula de un punto A a un punto B, y en otro momento se resuelve
suponiendo que la corriente circula de B a A, entonces los valores obtenidos de
corriente serı́an los mismos, pero cambiados de signo.
La conclusión a la que se puede llegar analizando el problema más formalmente, es la
siguiente.
Toda corriente que circula de un punto A a un punto B es equivalente a otra
corriente que circula del punto B al A y que tiene el mismo valor pero cambiado
de signo. Por tanto, toda corriente se puede sustituir por otra de sentido opuesto
y de mismo valor pero cambiado de signo. Ası́ pues, a efectos prácticos, cuando se
resuelve un circuito, el sentido que se le asigna a una corriente sólo determina el
signo que tendrá su valor.
4.4.
Más acerca de asociaciones
Cuando se hacen asociaciones de elementos, ya sean en serie o en paralelo, se pretende
simplificar ciertas zonas del circuito no relevantes para el cálculo que se pretende realizar.
Es lo que comentábamos en la sección 4.1: si por ejemplo queremos hallar la corriente que
58
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
V1
E
V2
A
C
R1
R5
R2
R6
IR6
IR3
B
F R3
D
R4
Figura 4.46: un circuito donde nos planteamos si asociar
Veq=V1-V2
E
C
R1
R5
R2
R6
IR6
IR3
D
B
F R3
R4
Figura 4.47: el circuito de la Figura 4.46, donde se han asociado las dos fuentes de tensión en
serie
atraviesa una determinada resistencia, todo lo ajeno a ella nos resulta molesto, en cierto modo
innecesario. Por tanto, si dichas partes del circuito ajenas se pudieran simplificar al máximo,
la labor de obtener el parámetro en el que estamos interesados, la corriente en la resistencia, se
podrı́a simplificar en gran medida.
A pesar de la tentación que puede suponer asociar elementos en un circuito sin pensar
en ello, sólo con el propósito de reducir su tamaño, hay que tener vista a la hora de realizar
una asociación. Cuando se hace una asociación de elementos, hay que tener en cuenta que se
pierde información del circuito original. No todo podı́an ser ventajas, claro. Supongamos
que tenemos un sencillo circuito, como el de la Figura 4.46.
En este circuito hay numerosos elementos que pueden ser asociados. Por ejemplo, las fuentes
V1 y V2 pueden ser asociadas en serie, las resistencias R3 y R4 pueden ser asociadas en serie,
las resistencias R1 y R2 pueden ser asociadas en serie, y las resistencias R5 y R6 pueden ser
asociadas en paralelo. A pesar de todo lo que se podrı́a simplificar el circuito si asociáramos
tantos elementos, hay que ser consciente en todo momento de qué es lo que se pretende obtener
del circuito. Si, por ejemplo, el problema consistiera en obtener la tensión en el punto A, asociar
en serie las fuentes de tensión nos darı́a problemas, dado que, al asociarlas en serie, los puntos
de conexión intermedios entre elementos desaparecen. Por ejemplo, tras asociarlas, el circuito
que quedarı́a serı́a el de la Figura 4.47.
En el circuito asociado es importante observar que los puntos intermedios a las fuentes
59
4.4. MÁS ACERCA DE ASOCIACIONES
V1
E
V2
A
C
R1
IReq
R2
Req=R5+R6
IR3
B
F R3
D
R4
Figura 4.48: el circuito de la Figura 4.46, donde se han asociado las resistencias en paralelo
asociadas desaparecen tras ser asociadas. Por contra, los puntos extremos, E y C, siguen manteniéndose inalterados. Es por ello que en este nuevo circuito no se podrı́a hallar la tensión en
el punto A, ya que dicho punto, tras la asociación, habrı́a desaparecido.
Es el mismo problema que existe con las resistencias R3 y R4 . Si dichas resistencias se asocian
en serie, si bien los puntos extremos, D y F siguen existiendo en el circuito simplificado (y por
tanto se podrı́a hallar en él los parámetros de tensión en F y en D), el punto B desaparecerı́a,
y ası́ la tensión en el punto no podrı́a hallarse en el modelo con la resistencia equivalente.
Por contra, cuando se asocian elementos en serie, la corriente que atraviesa el modelo simplificado sigue siendo la misma que la corriente que atraviesa el modelo original. Es decir, si
por ejemplo asociáramos las resistencias R3 y R4 , la corriente que circuları́a por la resistencia
equivalente (R3 +R4 ) seguirı́a siendo igual a IR3 , la corriente del circuito original. Tiene sentido
que sea ası́, ya que, cuando se asocian elementos en serie, la rama en la que se sitúan dichos
elementos sigue existiendo, y sigue siendo la misma que habı́a en el modelo sin simplificar.
Por tanto, la corriente que circula por ella debe ser la misma que en circuito sin los elementos
simplificados.
Por tanto, cuando se asocian elementos en serie, ya no se puede calcular la tensión
de los puntos intermedios existentes entre los elementos asociados, ya que dichos
puntos desaparecen en el modelo simplificado, pero por contra, la corriente que circula por el elemento equivalente es igual a la que circula por todos los elementos sin
asociar, y por tanto ésta sı́ se puede obtener directamente del modelo equivalente.
Las asociaciones en paralelo plantean un problema simétrico. Cuando se asocian elementos
en paralelo, hay ramas del circuito que desaparecen. Si bien los puntos extremos de los elementos
conectados en paralelo se mantienen inalterados, las ramas que conformaban la asociación en
paralelo desaparecen, aglutinándose en una sola. Ello genera una pérdida de información, a
saber, las corrientes que circulaban por cada una de las ramas de los elementos asociados en
paralelo (esto es parecido a la incapacidad de no poder calcular la tensión en nodos intermedios
en las asociaciones en serie). Supongamos, por ejemplo, que en el ejemplo que estamos tratando,
las resistencias R5 y R6 se asocian en paralelo, generando el circuito de la Figura 4.48.
En el circuito actual, como se puede apreciar, los puntos extremos de los elementos asociados
en paralelo, C y D, se mantienen inalterados. Por tanto, cualquier tensión referente a C o a D
en el circuito original podrı́a hallarse en el modelo simplificado. Ahora bien, ¿y si se quisiera
hallar, por ejemplo, la corriente IR6 del circuito original? Esa corriente era la que circulaba
por la rama de la resistencia R6 , pero dicha rama, en el modelo simplificado, ha desaparecido.
Ası́ pues, en el modelo equivalente, las corrientes que circulaban por cada una de las ramas de
los elementos asociados en paralelo dejan de tener sentido, y no pueden calcularse de forma
60
CAPÍTULO 4. ASOCIACIONES DE ELEMENTOS
directa.
En resumen, cuando se asocian elementos en paralelo, ya no se puede calcular las
corrientes que circulaban por las ramas de cada uno de los elementos asociados en
el modelo original, ya que dichas ramas, en el modelo equivalente, dejan de existir,
pero por contra, la tensión presente entre los extremos de los elementos asociados
sigue siendo la misma, ya que los puntos extremos de los elementos asociados no
desaparecen tras la asociación, y por tanto ésta sı́ se puede obtener del modelo
equivalente.
Capı́tulo 5
Resolución de circuitos en
condiciones de corriente continua
Este capı́tulo tiene como propósito el de proporcionar al lector dos métodos con los que
pueda resolver cualquier circuito de corriente continua. Uno de ellos, el método de los nudos.
El otro, el método de las mallas. Además, se darán una serie de pistas fundamentales que
es conveniente tener en cuenta siempre que se resuelven circuitos, sean del tipo que sean. Para
finalizar, tras las explicación de cada método, hay una considerable lista de ejercicios resueltos
para que se ponga en práctica todo lo que se ha explicado hasta el momento.
5.1.
Pistas para la resolución de circuitos
Cuando se resuelven circuitos, ya sean de corriente continua o no, hay una serie de ideas
que hay que tener en la cabeza permanentemente si no queremos quedarnos a medias sin saber
cómo acabar un circuito. Esas ideas, que deberán ser puestas en práctica conforme se hagan más
y más circuitos, ya han sido expuestas, pero no se les suele dar la importancia que requieren.
Esto es por lo que pasamos a repetirlas, y a incentivar que se tengan siempre en cuenta.
• Si una corriente circula de un punto A a un punto B a través de una resistencia R, su
expresión, según la Ley de Ohm, es:
IAB =
VA − VB
R
• Acerca de las fuentes de tensión, hay que tener en cuenta que una fuente impone una
ecuación de la forma V+ − V− = V alor de la f uente. Estas ecuaciones, en muchas circunstancias, hay que tenerlas en cuenta para poder resolver un circuito, ya que hay ciertas
situaciones en las que nos faltarán ecuaciones para resolver un sistema, y serán las fuentes
de tensión las que nos las proporcionen.
• Referente a las fuentes de corriente, hay que tener en cuenta que éstas también nos dan
información muy útil a la hora de resolver un circuito. Recordemos que una fuente de
corriente impone en la rama en la que se sitúa una corriente cuyo sentido es el indicado
por la flecha de la fuente, y cuyo valor es igual al de la fuente. Por todos los elementos de
la rama en la que está esa fuente circula esa corriente.
• A la hora de resolver un circuito, las corrientes se pueden suponer en cualquier sentido.
La única diferencia entre haber supuesto un sentido u otro para una corriente es el signo
que ésta tendrá. Positivo, si va en un sentido, y negativo, si va en el otro.
61
62
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
• Toda fuente de tensión puede sustituirse por otra que tiene la polaridad invertida respecto
a la original, y cuyo valor de tensión es el mismo, pero cambiado de signo.
• Toda corriente de un circuito es equivalente a otra corriente con el sentido de circulación
opuesto y con el mismo valor, pero cambiado de signo. Como consecuencia, toda fuente
de corriente se puede sustituir por otra cuya corriente es inyectada en el sentido opuesto
al de la original, y cuyo valor es el de la original, pero cambiado de signo.
• La toma de tierra de un circuito representa el punto donde la tensión es cero. Este dato
será necesario tenerlo en cuenta en muchas circunstancias para poder resolver el circuito.
• Todos los puntos de un circuito que están cortocircuitados entre sı́, están a la misma tensión. Esto es de vital importancia, ya que hay muchos extremos de elementos electrónicos
cortocircuitados, y por tanto la tensión que en ellos hay es la misma, permitiendo considerar la existencia de una sola incógnita, y no varias.
• En un circuito de corriente continua, un condensador puede sustituirse por un circuito
abierto, y una bobina, por un cortocircuito.
5.2.
Método de los nudos
El método de los nudos para la resolución de circuitos de corriente continua se basa, simplemente, en la aplicación de la ley de los nudos (sección 3.2) a los nudos del circuito que
se pretende resolver. Concretamente, se puede demostrar que para resolver un circuito con n
nudos, se requiere aplicar la ley de los nudos a n − 1 nudos del circuito. Si bien esto no es de
forma exacta cierto, en general se cumple. Cuando no se cumpla, veremos el por qué, y también
veremos que no tiene real importancia. Los pasos a seguir son:
• Suponer que por cada rama circula una corriente cuyo sentido de circulación está definido
por nosotros.
• Aplicar la ley de los nudos a los nudos del circuito.
• Sustituir la expresión de cada corriente del circuito por su valor dado por la Ley de Ohm,
teniendo en cuenta el sentido de circulación de las corrientes.
• Considerar la presencia de fuentes de corriente, de tensión, y la toma de tierra, y obtener
las ecuaciones que imponen.
• Resolver el sistema de ecuaciones obtenido. Debe ser un sistema cuyas incógnitas son
tensiones en el circuito.
5.2.1.
Método de los nudos, ejercicios
En esta sección se realizará una serie de ejercicios de circuitos de corriente continua mediante
el método de los nudos. Es de especial importancia que el lector adquiera soltura con este
método, ya que es uno de los pilares fundamentales de la resolución de todo tipo de circuitos,
no sólo de circuitos de corriente continua.
Ejercicio 5.1: Para el circuito de la Figura 5.1 se pide calcular:
a) Tensión en el nudo B.
63
5.2. MÉTODO DE LOS NUDOS
b) Potencia disipada por la resistencia de 5Ω.
c) Potencia generada o consumida por la fuente de corriente dependiente, e indicar si se trata
de potencia generada o consumida.
2Ω
2,5Ib
A
B
2Ω
Ib
10A
5Ω
9A
Figura 5.1: Ejemplo 5.1
Solución
El circuito mostrado presenta tres fuentes de corriente, dos normales, y una dependiente.
Además, el circuito contiene 3 resistencias. Como detalle especial, notar que el valor de la fuente
de corriente dependiente depende de la corriente Ib dibujada, que es la corriente que circula por
la resistencia de 5Ω, y hacia abajo.
Para resolver el circuito por el método de los nudos, primero debemos definir las corrientes
que circulan por las ramas del circuito. En el caso de las ramas de las fuentes de corriente,
dichas corrientes no son ni siquiera incógnitas, ya que están definidas por las mismas fuentes.
La Figura 5.2 muestra el circuito original, al que se le han asignado corrientes aleatorias en sus
ramas.
Como curiosidad, si la corriente I3 se hubiera supuesto circulando en sentido contrario al
dibujado, su valor habrı́a tenido que ser de −10A: la corriente I3 habrı́a sido equivalente a la
corriente que hay en la rama, que es de 10A hacia arriba. Como I3 habı́a sido supuesta hacia
abajo, el único modo de ser equivalente a la de 10A hacia arriba es haciendo que su valor de
corriente tenga signo opuesto, tal y como se explicó en la sección 4.3.5.
I1
2Ω
A
B
I5=9A
I4=2,5Ib
2Ω
I2
Ib
10A
I3=10A
5Ω
9A
C
Figura 5.2: Ejemplo 5.1 con corrientes aleatorias asignadas a cada rama
64
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Ahora, si simplemente aplicamos la ley de los nudos a los nudos A y B, obtenemos las
siguientes ecuaciones:
I2 + I3 + I4 = I1
I5 + I1 = Ib + I4
(Nudo A)
(Nudo B)
Ya que en el nudo A, sólo la corriente I1 sale, mientras que las demás entran, y en el nudo B
las corrientes I5 e I1 entran mientras que las corrientes Ib e I4 salen.
Teniendo en cuenta además que, según las fuentes de corriente del circuito:
I3 = 10
I5 = 9
I4 = 2,5Ib
Se tiene que las ecuaciones de los nudos A y B quedan como:
I2 + 10 + 2,5Ib = I1
9 + I1 = Ib + 2,5Ib
(Nudo A)
(Nudo B)
Aplicando ahora la Ley de Ohm para obtener el valor de cada corriente, y considerando que el
punto C, al ser la toma de tierra, implica que VC = 0, las ecuaciones de los nudos quedan en:


V
A − VB 


!


I1 =





VA − VB
V
V
B
A



2







 2 + 10 + 2,5 5 =
VC − VA 
2
I2 =
!
⇒
2



V
V
V
−
V
B
B
A
B



VB − VC 


=
+ 2,5





9 +
Ib =


2
5
5


5


VC = 0
Sistema de ecuaciones que depende de las incógnitas VA y VB , cuya solución es:
VA = 30V, VB = 20V
Por tanto, la tensión en el nodo B es de 20V .
¿Cuál es la potencia disipada en la resistencia de 5Ω? Recordemos que el valor de la potencia
disipada por una resistencia se puede obtener mediante la ecuación (1.3). Dicha ecuación decı́a
que la potencia consumida o emitida por una corriente que se desplaza del punto A al punto B
es igual a:
P (t) = IAB (t)VAB (t)
En este caso queremos conocer el valor de la potencia consumida por la resistencia de 5Ω, con
lo cual necesitamos conocer tanto el valor de la diferencia de tensión que soporta la resistencia
como el valor de la corriente que la atraviesa. El valor de la diferencia de tensión que soporta
la resistencia ya lo conocemos, ya que la tensión que soporta en un punto, C, es 0V , y el valor
de tensión en el otro punto, B, es de 20V . Queda por tanto obtener el valor de la corriente que
lo atraviesa, la corriente Ib . Sabemos que, según la Ley de Ohm:
Ib =
VB − 0
VB − VC
=
= 4A
5
5
Como la corriente Ib circula desde el punto B al C, hay que considerar que la diferencia de
tensión que hay que usar en la fórmula de la potencia es VBC = VB − VC = 20 − 0 = 20V . Por
tanto, la potencia de la resistencia queda:
P = IBC VBC = Ib VBC = 4 · 20 = 80W
65
5.2. MÉTODO DE LOS NUDOS
Como la potencia es positiva, se deduce, como era de esperar, que la potencia es consumida,
es decir, la resistencia absorbe energı́a del resto del circuito, que en su caso particular, por ser
resistencia, emite en forma de calor.
En el caso de la fuente dependiente de corriente, para obtener su valor de potencia generada
o consumida, basta aplicar la expresión (1.3), considerando la corriente que atraviesa la fuente
de corriente y la tensión que soporta entre sus terminales.
La corriente que la atraviesa es 2,5Ib , y la diferencia de tensión a tener en cuenta, según
el sentido de circulación de la corriente 2,5Ib , es VAB = VA − VB . Por tanto, la expresión (1.3)
queda en:
P = 2,5Ib (VA − VB ) = 2,5 · 4(30 − 20) = 100W
Es decir, la potencia de la fuente de corriente es de 100W , positiva, y por tanto actúa como un
elemento pasivo, consumiendo energı́a del resto del circuito.
Ejercicio 5.2: Para el circuito de la Figura 5.3 se pide:
a) Determinar el valor y el sentido de la corriente que circula por la resistencia de 5Ω.
b) Verificar que se cumple el principio de conservación de la energı́a.
10A
5Ω
6V
2Ω
+
−
10V
2Ω
6A
4Ω
Figura 5.3: Ejemplo 5.2
Solución
Inicialmente, y como debe hacerse siempre que se resuelve un circuito por el método de los
nudos, se debe suponer que por cada rama del circuito circula una corriente con un sentido
determinado (y elegido aleatoriamente por nosotros). En el ejemplo actual, el resultado es el
mostrado en la Figura 5.4. Además, para simplificar, los extremos de la rama donde está la
resistencia de 5Ω se han movido y juntado con los nodos que hay inmediatamente debajo. Si
no se hubiera hecho ası́, la resolución no habrı́a sido más compleja.
Ahora debemos aplicar la ley de los nudos a cada uno de los nudos del circuito. En general,
recordemos, la ley se aplica a todos los nudos del circuito menos a uno. En este caso, hay 4
66
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
10A
I8
5Ω
2Ω
10V
I2
I5
I4
2Ω
C
+
−
A
I1
6V I
7
B
I3
6A
I6
4Ω
D
Figura 5.4: Ejemplo 5.2; corrientes asignadas a cada rama
nudos, el A, B, C y D, ası́ que se aplicará la ley a los tres primeros, siendo el D el nodo que no
utilizaremos.
I1 = I2 + I7 + I8
I2 + I4 = I3 + I5
I5 + I6 + I7 + I8 = 0
(Nudo A)
(Nudo B)
(Nudo C)
Ahora se debe sustituir cada una de las corrientes utilizadas en esa ecuación, por la expresión
que indica la Ley de Ohm, obteniendo un conjunto de ecuaciones con demasiadas incógnitas,
y que será simplificado analizando las ecuaciones asociadas a las fuentes de corriente y fuentes
de tensión.


V
−
V


A
B






 I2 =
VA − VB VA − VC



2



+
+ I8
I1 =






V
−
V
D 


2
5


 I3 = B
VB − VD
VA − VB
2
⇒
+ I4 =
+ I5
V
−
V



D
C 
2
2





I
=
6






4
 I5 + V D − V C + V A − V C + I8 = 0






V
−
V
A
C


4
5


I7 =
5
Claro que, como se puede apreciar, el conjunto actual de ecuaciones tiene demasiadas incógnitas
para el número de ecuaciones existentes. Debemos buscar más ecuaciones que nos permitan
resolver el sistema.
Tal y como se explicó en la introducción de la sección 5.2, el siguiente paso a la hora de
resolver el circuito es tener en cuenta tanto a las fuentes de tensión como de corriente, junto
con la toma de tierra, y ver qué ecuaciones imponen.
Fijémonos primero en las fuentes de corriente.
La fuente de corriente de 10A, la de arriba, impone por su rama una corriente de 10A
que circula hacia la derecha. Si nos fijamos, esa corriente coincide con la que nosotros hemos
llamado I8 , y por tanto,I8 = 10. Por supuesto, si la corriente I8 la hubiéramos supuesto circular
en un sentido contrario al dibujado, es decir, hacia la izquierda, su valor habrı́a sido de −10A:
la fuente de corriente se podrı́a haber sustituido por una de igual valor y cambiado de signo
(−10A), pero que circulase hacia la izquierda. En ese caso la corriente de esa fuente coincidirı́a
con la nueva I8 (la que circula hacia la izquierda), y por tanto, I8 habrı́a valido −10A.
67
5.2. MÉTODO DE LOS NUDOS
La fuente de corriente de 6A impone una corriente de valor 6A que circula hacia arriba en
la rama en la que se sitúa. Esa corriente coincide con la corriente que hemos llamado I4 , que
es la que circula por la rama de esa fuente de corriente. Por tanto, I4 = 6.
Las fuentes de tensión, por otro lado, nos proporcionan otras dos ecuaciones necesarias para
resolver el circuito. Consideremos, además, que el punto D, por ser tierra, cumple que VD = 0.
Es importante recordar que no sólo el punto exacto como D va a estar a 0 voltios, sino que todos
los puntos que estén cortocircuitados a D, véase, todos los extremos inferiores de: la fuente de
tensión de 10V , la fuente de corriente de 6A, la resistencia de 4Ω y la resistencia de 2Ω situada
en paralelo con la fuente de 6A. Dicho de otro modo, la tensión en todos esos puntos es igual
a VD , que a su vez es igual a 0 voltios.
La fuente de tensión de 10V impone la ecuación VA − VD = 10 por definición, es decir, la
diferencia de tensión entre el polo positivo (en su polo positivo hay VA voltios) y el negativo
(VD ) es igual al valor de la fuente, 10V . Como además VD = 0, la ecuación se reduce a VA = 10
La fuente de tensión de 6V impone la ecuación VC −VB = 6, es decir, la diferencia de tensión
entre el polo positivo (VC ) y el negativo (VB ) es igual al valor de la fuente, 6V .
Las últimas ecuaciones obtenidas son:
I8 = 10, I4 = 6, VA = 10, VC − VB = 6, VD = 0
Ahora resta juntar esas ecuaciones con las ya obtenidas para cada nudo. Si hacemos lo propio
nos queda:

10 − VB 10 − VC


+
+ 10
I1 =



2
5


 10 − VB
VB
+6=
+ I5
2
2


− VC 10 − VC



+
+ 10 = 0
I5 +


4
5

VC − VB = 6
Sistema de 4 ecuaciones con 4 incógnitas de cuya resolución resultan los valores:
VB = 14V, VC = 20V, I1 = 6A, I5 = −3A
Nos pedı́an el valor y el sentido de circulación de la corriente que circula por la resistencia de
5Ω. En nuestro caso hemos supuesto que dicha corriente, I7 , circula hacia la derecha. Por tanto,
si aplicamos la Ley de Ohm para obtener su valor, tenemos que:
I7 =
VA − VC
10 − 20
=
= −2A
5
5
Por tanto, puede decirse que la corriente que atraviesa la resistencia de 5Ω es una corriente de
valor −2A, y que circula hacia la derecha. Si tenemos en cuenta que toda corriente es equivalente
a otra del mismo valor pero cambiado de signo, y de sentido de circulación opuesto, se puede
decir que, equivalentemente, la corriente es de 2A (mismo valor pero cambiado de signo), y que
circula hacia la izquierda (sentido de circulación opuesto).
Para verificar que se cumple el principio de conservación de la energı́a, basta comprobar,
como se explicó en la sección 2.6, que las potencias consumidas en cada instante de tiempo son
iguales a las potencias generadas, en cada uno de los elementos del circuito.
Recordemos que la potencia generada o consumida por cada elemento del circuito viene dada
por la expresión (1.3), y en el caso de las resistencias, más particularmente, por la expresión
(2.2).
Para el cálculo de la potencia en las resistencias usaremos la expresión que emplea la corriente.
68
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
• En la resistencia de 5Ω, la corriente que circula es I7 , de modo que:
P = I7 2 R = (−2)2 5 = 20W
• En la resistencia de 2Ω situada en la rama A-B, la corriente que circula es I2 , de modo
que:
!2
!2
10
−
14
V
−
V
A
B
2=
2 = 8W
P = I2 2 R =
2
2
Si bien en este ejemplo no tiene importancia la expresión de I2 al estar elevada al cuadrado,
es importante recalcar que, dado que I2 se ha supuesto circulando del nodo A al nodo B,
su expresión es (VA − VB )/2.
• En la resistencia de 2Ω situada en la rama D-B, la corriente que circula es I3 , de modo
que:
!2
!2
V
−
V
14
−
0
B
D
P = I3 2 R =
2=
2 = 98W
2
2
Si bien en este ejemplo no tiene importancia la expresión de I3 al estar elevada al cuadrado,
es importante recalcar que, dado que I3 se ha supuesto circulando del nodo B al nodo D,
su expresión es (VB − VD )/2. Además, dado que D coincide con la tierra, la tensión en D
es 0 (VD = 0).
• En la resistencia de 4Ω, la corriente que circula es I6 , de modo que:
P = I6 2 R =
VD − VC
4
!2
4=
0 − 20
4
!2
4 = 100W
Para el cálculo de las potencias en las fuentes de tensión y de corriente, la cual podrá ser
generada o consumida, usaremos la ecuación (1.3).
• En la fuente de corriente de 10A, la potencia es:
P = I8 VAC = I8 (VA − VC ) = 10(10 − 20) = −100W
Como la potencia es negativa, se trata de energı́a que la fuente de corriente genera, es decir,
energı́a que pierde para ser aprovechada por el resto del circuito. Es importante recordar
que la corriente que aparece en la expresión de la potencia tiene el mismo sentido que
la diferencia de tensión que también aparece, es decir, si la corriente circula de A a B,
entonces la diferencia de tensión es VAB = VA − VB (en nuestro caso de A a C).
• En la fuente de corriente de 6A, la potencia es:
P = I4 VDB = I4 (VD − VB ) = 6(0 − 14) = −84W
Como la potencia es negativa, se trata de energı́a que la fuente de corriente genera, es decir,
energı́a que pierde para ser aprovechada por el resto del circuito. Es importante recordar
que la corriente que aparece en la expresión de la potencia tiene el mismo sentido que
la diferencia de tensión que también aparece, es decir, si la corriente circula de A a B,
entonces la diferencia de tensión es VAB = VA − VB (en nuestro caso de D a B).
69
5.2. MÉTODO DE LOS NUDOS
• En la fuente de tensión de 10V , la potencia es:
P = I5 VDA = I5 (VD − VA ) = 6(0 − 10) = −60W
Como la potencia es negativa, se trata de energı́a que la fuente de tensión genera, es decir,
energı́a que pierde para ser aprovechada por el resto del circuito. Es importante recordar
que la corriente que aparece en la expresión de la potencia tiene el mismo sentido que
la diferencia de tensión que también aparece, es decir, si la corriente circula de A a B,
entonces la diferencia de tensión es VAB = VA − VB (en nuestro caso de D a A).
• En la fuente de tensión de 6V, la potencia es:
P = I5 VBC = I5 (VB − VC ) = (−3)(14 − 20) = 18W
Como la potencia es positiva, se trata de energı́a que la fuente de tensión consume, es decir,
energı́a que absorbe del resto del circuito. Es importante recordar que la corriente que
aparece en la expresión de la potencia tiene el mismo sentido que la diferencia de tensión
que también aparece, es decir, si la corriente circula de A a B, entonces la diferencia de
tensión es VAB = VA − VB (en nuestro caso de B a C).
Las potencias consumidas (las positivas) son 20W , 8W , 98W , 100W y 18W , que suman en
total 244W . Las potencias generadas (las negativas) son 100W , 84W y 60W , que suman en
total 244W . Se puede apreciar que la potencia consumida por los elementos pasivos del circuito
es igual a la potencia generada a su vez por los elementos activos, es decir, se cumple el principio
de conservación de la energı́a.
Ejercicio 5.3: Para el circuito de la Figura 5.5 se pide obtener la tensión en el nodo A.
1KΩ
+
10V −
1KΩ
1KΩ
A
1KΩ
10mA
+
10V −
Figura 5.5: Ejemplo 5.3
Solución
En este ejemplo se va a aplicar el método de los nudos tal y como se ha explicado con
anterioridad. En primer lugar, debemos asignar corrientes a cada una de las ramas del circuito.
Recordemos que los sentidos de circulación de esas corrientes los asignamos de forma aleatoria.
Por ejemplo, podemos suponer que las corrientes presentes en las ramas del circuito son las
mostradas en la Figura 5.6.
Asignadas las corrientes a cada rama del circuito, basta aplicar la ley de los nudos a aquellos
nudos que sean de interés. Recordemos que el proceso de resolución de un circuito es bastante
70
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
C
1KΩ
A
I1
+
10V −
E
1KΩ
B
I3
1KΩ
I4
1KΩ
I5
10mA
D
I2
+
10V −
F
Figura 5.6: Ejemplo 5.3 con corrientes asignadas a cada rama
mecánico: de un modo u otro tenemos que obtener suficientes ecuaciones para poder resolver
un sistema con las incógnitas buscadas. En el fondo, no importa el cómo se obtienen esas ecuaciones, siempre y cuando sean válidas. El método de los nudos no es más que un procedimiento
sistemático para obtener las ecuaciones necesarias.
Tal y como se hizo en las secciones donde se analizaban las asociaciones en paralelo de los
elementos fundamentales, el circuito podrı́a haberse redibujado de modo que el nodo A y el
nodo B se juntaran: tal y como se dijo, siempre que no se creen y se destruyan conexiones
en un circuito, éste puede redibujarse como parezca más conveniente. En nuestro ejemplo, sin
embargo, se ha optado por el camino más complicado. Ası́ pues, si aplicamos la ley de los nudos
a los nudos A y B, obtenemos:
I1 + I2 = I3
I3 + I4 = I5
(Nudo A)
(Nudo B)
Ahora aplicamos la Ley de Ohm para cada una de las corrientes, teniendo en cuenta el sentido
de circulación de éstas:

VC − VA


I
=

1


1000

0 − VA
I2 =

1000



V

 I5 = B − V D
1000








V − VA 0 − VA

 C
+
= I3
1000
1000
⇒



I + I = VB − VD

3
4


1000

El 0 presente en la expresión de I2 se debe a la presencia de la toma de tierra, donde la tensión es
cero. Además, a I3 no se le puede aplicar la expresión de la Ley de Ohm, dado que la resistencia
presente entre el nudo A y el B es cero. Realmente, si nos fijamos con detalle, lo que hay entre
A y B es un cortocircuito. En un cortocircuito no tiene sentido aplicar la Ley de Ohm, ya que,
no sólo ocurre que la resistencia es nula, sino que la diferencia de tensión también es nula. En
efecto, en nuestro ejemplo, al estar A y B cortocircuitados la tensión en A serı́a la misma que
en B, y la expresión de I3 se reducirı́a a (VA − VB )/R = {0/0}, indeterminación que debemos
rehuir a toda costa, y debido a la cual I3 se queda tal cual en las ecuaciones.
I4 sı́ podrı́a expresarse en términos de la Ley de Ohm. Ahora bien, si nos damos cuenta,
podemos ver que I4 coincide justamente con la corriente que inyecta la fuente de corriente de
10mA: la fuente impone una corriente de 10mA, y hacia arriba, en toda la rama en la que se
sitúa. Por tanto, al ser I4 una corriente con el mismo sentido que la de la fuente, su valor viene
determinado directamente por ésta, y es de 10mA. De este modo I4 desaparece del sistema.
71
5.2. MÉTODO DE LOS NUDOS
Si, por último, consideramos que los nodos A y B están cortocircuitados, y que por tanto
VA = VB , las ecuaciones de los nudos se reducen a:
VC − VA 0 − VA
+
= I3
1000
1000
VA − VD
I3 + 10 · 10−3 =
1000
(Nudo A)
(Nudo B)
A pesar de todo lo hecho, todavı́a tenemos demasiadas incógnitas para resolver este sistema de
ecuaciones. Para obtener las ecuaciones que nos faltan, podemos analizar las fuentes de tensión
presentes en el circuito, y ver qué ecuaciones imponen (recuérdese que una fuente de tensión
nos dice que la diferencia de tensión entre el polo positivo y el negativo es igual al valor de la
fuente):
VC − VE = 10
VD − VF = 10
La primera ecuación se corresponde con la fuente de la izquierda, mientras que la segunda se
corresponde con la fuente de la derecha. Estas ecuaciones se pueden simplificar considerando
que los puntos E y F están cortocircuitados con la toma de tierra, y por tanto VE = VF = 0.
Las ecuaciones quedan, por tanto:
VC = 10
VD = 10
Las cuales, si las sustituimos en las ecuaciones del nudo A y del nudo B:

10 − VA 0 − VA


+
= I3
1000
1000

I + 10 · 10−3 = VA − 10
3
1000
Sistema de dos ecuaciones con dos incógnitas, tras cuya resolución se obtiene.
VA = 10V, I3 = −0,01A
Es decir, la tensión en el nudo A es de 10V .
Ejercicio 5.4: Para el circuito de la Figura 5.7, se pide hallar la resistencia equivalente medida
entre los terminales A y B.
Solución
En los ejercicios resueltos hasta ahora no se ha realizado ningún tipo de asociación de
elementos. En este ejemplo se nos está pidiendo que obtengamos la resistencia equivalente,
medida entre las terminales A y B, al conjunto de resistencias (que por cierto es bien feo), de
la Figura 5.7. El problema al que nos enfrentamos es que, en este circuito, no se puede llevar a
cabo asociaciones en serie o asociaciones en paralelo. Por ejemplo, las dos resistencias de 2KΩ
no pueden asociarse en serie, dado que en el nodo que las conecta confluye una resistencia de
1KΩ, y por tanto no se consideran en la misma rama. En general, como se ha dicho, no se
72
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
A
1KΩ
1KΩ
2KΩ
1KΩ
2KΩ
B
Figura 5.7: Ejemplo 5.4
A
A
1KΩ
1KΩ
2KΩ
1KΩ
B
Req
2KΩ
B
Figura 5.8: el conjunto de resistencias original debe ser equivalente a una cierta Req
pueden asociar las resistencias de este circuito, ni en serie ni en paralelo. Entonces, ¿cómo se
obtiene la resistencia equivalente medida entre A y B?
Recordemos que el proceso de obtener un elemento equivalente a otros dados es algo más
general, no limitado a asociaciones en serie o en paralelo. Si bien en la mayorı́a de las ocasiones
los elementos pueden ser asociados en serie o en paralelo, hay casos especiales en los que
hay que recurrir al método general para obtener un elemento equivalente a otros dados. Ese
procedimiento se explicó en la sección 4.1, y de hecho fue aplicado para obtener las ecuaciones
de las asociaciones en serie y en paralelo de las secciones 4.2 y 4.3.
Se dice que dos subcircuitos con dos terminales externos cada uno son equivalentes, si cuando
a ambos se les aplica la misma tensión entre los dos terminales externos, entonces las corrientes
de entrada y de salida son iguales en ambos circuitos (es decir, las relaciones entre la tensión
aplicada a las terminales y la corriente de entrada o salida son iguales en ambos circuitos).
Tal y como se explicó en la sección 4.1, si tal condición se cumple, ambos circuitos muestran
un comportamiento equivalente, y por tanto uno puede sustituirse por el otro, de modo que el
resto del circuito (aquél al que se conecta el subcircuito) mostrará el mismo comportamiento
que con el circuito original.
Concretamente, nosotros buscamos que el circuito de la Figura 5.7, sea equivalente a una
resistencia de valor, a hallar, tal y como se muestra en la Figura 5.8.
Tenemos por tanto dos circuitos que queremos que sean equivalentes, los mostrados en
la Figura 5.8. Impondremos, por tanto, la condición de equivalencia antes mencionada, para
ası́ obtener el valor de Req que hace que ambos circuitos sean en efecto equivalentes.
Si ambos circuitos son equivalentes debe cumplirse que, ante la misma tensión de entrada,
las corrientes de entrada y de salida sean la misma en ambos circuitos (Figura 5.9).
La Figura 5.9 representa a ambos circuitos, a los que se les ha conectado, en sus terminales
de entrada, una misma tensión. Ello simula la parte de bajo la misma tensión de entrada.
73
5.2. MÉTODO DE LOS NUDOS
I1
A
A
1KΩ
V
I2
1KΩ
2KΩ
+
−
V
1KΩ
+
−
2KΩ
Req
I2
B
B
I1
Figura 5.9: procedimiento para obtener el valor de Req
I
A
1KΩ
V
+
−
I1 I2
1KΩ
2KΩ
D
C
I3
I4
I5
1KΩ
2KΩ
B
I
Figura 5.10: circuito original, para obtener su corriente de entrada
Hecho esto, para imponer la equivalencia hay que forzar que la corriente de entrada del circuito
original, I1 , sea igual a la corriente de entrada del circuito equivalente, I2 . Si bien se ha hablado
de corriente de entrada, se podrı́a haber hablado igualmente de corriente de salida. Obviamente,
para cada uno de los circuitos se cumple que la corriente de entrada es igual a la de salida (toda
la corriente que entra por una de las terminales de un circuito debe ser igual a la que sale por
el otro terminal), y de ahı́ que se hayan dibujado repetidas en la Figura 5.9.
Ası́ pues, pasemos a obtener, en el circuito original, cuál es el valor de la corriente de entrada
I1 bajo la acción de una fuente de tensión de valor V (Figura 5.10). Para mayor simplicidad a
la hora de resolver el circuito, se ha renombrado la corriente I1 (corriente de entrada o de salida)
a I. Para evitar confusiones, considérese que los nombres de las corrientes de este circuito no
tienen nada que ver con los nombres de las corrientes de los circuitos antes mostrados.
Para resolver el circuito y obtener el valor de la incógnita I se empleará el método de los
nudos. El método de los nudos va a aplicarse a 3 nudos de interés (el circuito tiene 4, ası́ que
se aplica a 3, todos menos uno):
I = I1 + I2
I = I3 + I5
I2 + I4 = I5
(Nudo A)
(Nudo B)
(Nudo C)
74
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Consideremos ahora la Ley de Ohm para cada una de las corrientes (menos para I, para la cual
no tiene sentido aplicar la Ley de Ohm al no haber resistencia en la rama por la que circula).


V
−
V


A
D

 I =


1




1000







VA − VD VA − VC
V
−
V
A
C






+
I
=
I
=



2





1000 
1000
1000



VD − VB
VD − VB VC − VB
⇒ I=
I3 =
+


1000 
1000
2000









V
−
V
VC − VB
V
−
V
V
−
V



D
C
D
C
A
C





+
=
I4 =



2000 
1000
2000
2000





VC − VB 



 I5 =
2000
Queda por considerar las ecuaciones impuestas por la toma de tierra y la fuente de tensión. La
toma de tierra impone VB = 0, y la fuente de tensión VA − VB = V , que por ser VB = 0 queda
en VA = V . Si se aplica a las ecuaciones de los tres nudos, se tiene:

V − VD V − VC


I=
+



1000
1000

VB = 0
VD
VC
⇒ I=
+
VA = V

1000 2000




 V − VC + VD − VC = VC
1000
2000
2000
Sistema de tres ecuaciones con tres incógnitas, que, sin que sirva de precedente, va a ser resuelto.
Las ecuaciones del nudo A y B pueden igualarse (ambas son iguales a I). De este modo nos
liberamos de una de las incógnitas, quedando:

VD
VC
V − VD V − VC


+
=
+
1000
1000
1000 2000

 V − VC + VD − VC = VC
1000
2000
2000
De la primera ecuación es fácil deducir que:
4
VC = (V − VD )
3
(5.1)
La segunda ecuación puede simplificarse, quitando los denominadores, y agrupando términos:
2V − 2VC + VD + VC = VC ⇔
2V + VD = 4VC
Si ahora se sustituye la ecuación (5.1) en la ecuación (5.2), queda:
2V + VD =
De donde se obtiene:
VD =
16
(V − VD )
3
10
V
19
Usando (5.1) y la expresión de VD se deduce:
VC =
12
V
19
(5.2)
75
5.2. MÉTODO DE LOS NUDOS
A
I
+
−
V
Req
I
B
Figura 5.11: circuito simplificado, para obtener su corriente de entrada
Usando VD y VC , junto con la ecuación del nudo B:
VD
VC
+
⇔
1000 2000
2000I = 2VD + VC ⇔
I=
2000I =
12
20
V + V ⇔
19
19
2
I=
V
2375
Este valor de I se corresponde con el valor de la corriente de entrada I1 en el circuito original.
Nos queda por obtener el valor de la corriente de entrada en el circuito con el modelo equivalente.
La Figura 5.11 representa el circuito simplificado, con la resistencia equivalente.
En el circuito simplificado es trivial obtener la corriente de entrada. Se deduce de forma
directa de la Ley de Ohm:
V
I=
Req
Este valor de I se corresponde con la corriente de entrada I2 del circuito simplificado.
Obtenidas las corrientes de entrada de cada uno de los circuitos, queda imponer la condición
de que sean iguales, de donde se obtiene el valor de la resistencia equivalente buscada:
I1 = I2 ⇔
V
2
⇔
V =
2375
Req
Req = 1187,5Ω
Ejercicio 5.5: Para el circuito de la Figura 5.12, se pide obtener las tensiones en los puntos
A y B.
Solución
El circuito se resolverá mediante el método de los nudos. En primer lugar, definimos una
corriente para cada rama del circuito. Recordemos que a las corrientes definidas se les asignan
sentidos aleatorios, sin influir esto en el resultado final. Un ejemplo de corrientes serı́a el de la
Figura 5.13.
76
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1000Ω
A
1000Ω
B
10V
1000Ω
1000Ω
20mA
20V
Figura 5.12: Ejemplo 5.5
D
1000Ω
A
I1
1000Ω
I3
I4
10V
I2
B
20mA
1000Ω
I5
1000Ω
20V E
C
Figura 5.13: Ejemplo 5.5, corrientes asignadas a cada rama
Asignadas las corrientes a cada rama, se aplica el método de los nudos a todos los nudos de
interés. En este caso, los nudos de interés son A y B:
I1 + I2 + I3 = 0
I3 = I4 + I5
(Nudo A)
(Nudo B)
Ahora aplicamos la Ley de Ohm para obtener las expresiones de cada una de las corrientes
dibujadas.


V
−
V


A
D




I1 =




1000






VA − VB
VA − VB 
V − VD



 I3 =
 A

+ I2 +
=0
1000
1000
1000
⇒
VB − VE 



 VA − VB = VB − VE + VB − VC



I4 =



1000 
1000
1000
1000






V
−
V
B
C


 I5 =

1000
Actualmente el sistema de ecuaciones no puede resolverse, pues tiene demasiadas incógnitas.
Para simplificarlo, analizaremos las fuentes de tensión y de corriente presentes en el circuito.
La fuente de corriente de 20mA inyecta en la rama en la que se sitúa una corriente de 20mA,
hacia arriba. Nosotros, sin embargo, hemos supuesto que la corriente que circula por la rama de
la fuente de corriente, I2 , va hacia abajo. Por tanto, ambas corrientes no coinciden, de modo que
no puede decirse que I2 = 20 · 10−3 . Sin embargo, sabemos que la fuente de corriente de 20mA
puede sustituirse por otra fuente equivalente (sección 4.3.5), con el mismo valor de corriente
pero cambiado de signo, y con el sentido de circulación opuesto. Si hacemos eso, entonces la
fuente de corriente original puede sustituirse por otra de −20mA, y que apunta hacia abajo.
Ası́, tendrı́amos que la corriente inyectada por esta fuente equivalente ya sı́ coincide con la
77
5.2. MÉTODO DE LOS NUDOS
corriente I2 , y por tanto se puede decir que I2 = 20 · 10−3. Existen otras alternativas para llegar
a esta conclusión. Tal y como se explicó en la sección 4.3.5, toda corriente es equivalente a otra
de sentido de circulación contrario y de valor cambiado de signo. Sabemos que en una rama sólo
puede existir una única corriente. En el caso de la rama de la fuente de corriente, esa corriente
es de 20mA y hacia arriba. La corriente I2 , al estar en la rama de la fuente de corriente, ha de
ser una corriente equivalente a la corriente que inyecta la fuente de corriente (ya que en una
rama sólo puede haber una corriente). Al tener I2 un sentido de circulación opuesto al de la
corriente inyectada por la fuente, para ser equivalente a ésta ha de tener un valor de corriente
de signo opuesto al de la fuente, es decir, I2 = −20 · 10−3 .
Otra alternativa para resolver el circuito habrı́a sido la de suponer, desde el principio, que
I2 circula hacia arriba, de modo que directamente I2 = 20 · 10−3 . Sin embargo, en este caso, la
ecuación del nudo A habrı́a sido distinta.
De la fuente de corriente de 10V se deduce que VD − VC = 10; de la de 20V , se deduce
que VE − VC = 20, y de la toma de tierra se deduce que VC = 0. Las dos primeras ecuaciones,
por tanto, quedan en VD = 10, VE = 20. Juntando todas las ecuaciones hasta el momento, las
ecuaciones del nudo A y del nudo B se simplifican:



−3
I
=
−20
·
10


V − 10
VA − VB
2



−3

 A

+
20
·
10
+
=0
VD = 10
1000
1000
⇒
VE = 20




 VA − VB = VB − 20 + VB − 0



VC = 0
1000
1000
1000
Sistema de dos ecuaciones con dos incógnitas, de cuya resolución se obtiene:
VA = 22V, VB = 14V
Ejercicio 5.6: En el circuito de la Figura 5.14, obtener la relación que debe existir entre las
resistencias para que por la resistencia R5 no circule corriente alguna.
R1
R2
V
R3
R5
R4
R6
Figura 5.14: Ejemplo 5.6
Solución
Éste es un ejercicio bastante largo y bastante feo. Que tenga que decirlo me revuelve el
estómago, pero la gente suele equivocarse mucho en este ejercicio por la falta de práctica en el
manejo de ecuaciones simples, como las que aquı́ veremos. Hay bastantes operaciones, de modo
que cualquier fallo en una fase temprana provoca un resultado erróneo. Ası́ pues, se recomienda
proceder con cuidado.
78
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
E
R1
A
I1
V
R2
I2 I3
R3
R5
C
R4
I6
I4 I5
D
R6
I1
B
Figura 5.15: Ejemplo 5.6, corrientes asignadas a cada rama
Antes de comenzar el ejercicio, debemos fijarnos en que no nos han dado ninguna toma
de tierra. En general, la toma de tierra forma parte del enunciado del ejercicio, pero hay
situaciones, como en la actual, en la que nos encontramos con un circuito sin tierra. De todos
modos, no se trata de un gran problema. Recordemos que el dónde colocar la toma de tierra
no influye en el comportamiento del circuito, sino que simplemente nos daba la capacidad
para poder obtener tensiones puntuales, y no limitarnos a diferencias de tensión. Como en este
ejemplo no se nos pide ninguna tensión, o algo similar, la localización de la toma de tierra no
tendrá importancia alguna, de modo que la colocaremos, pues por ejemplo, abajo. La Figura
5.15 muestra el circuito con la toma de tierra ası́ como con las corrientes asignadas para su
resolución mediante el método de los nudos.
¿Qué buscamos en este circuito? El enunciado nos pide hallar la relación que debe haber
entre las resistencias para que la corriente I6 (la que circula por R5 ) sea nula. Ası́ pues, nuestro
objetivo es, partiendo de la hipótesis de que I6 = 0, obtener una ecuación en la que intervengan
solamente resistencias, y que relacione sus valores. Quizás sea difı́cil proceder como estamos
acostumbrados, ya que no tenemos una incógnita conocida que despejar, y por tanto no sabemos
muy bien cómo movernos. A pesar de ello si mantenemos en mente la idea de obtener una
ecuación donde sólo aparezcan resistencias, ası́ como que I6 = 0, será fácil llegar al resultado
esperado.
Para resolver el problema aplicaremos la Ley de Ohm a tres nudos del circuito, a saber, los
nudos C, B y D.
Las ecuaciones de dichos nudos son:
I2 = I6 + I4
I1 = I4 + I5
I3 + I6 = I5
(Nudo C)
(Nudo B)
(Nudo D)
79
5.2. MÉTODO DE LOS NUDOS
Ahora podemos aplicar la Ley de Ohm para obtener la expresión de cada una de las corrientes
de esas ecuaciones:


V
−
V


E
A




I1 =




R
1







VC − VB
VA − VC
V
−
V



A
C






= I6 +
I2 =






R2
R4



 R2


VA − VD
VE − VA VC − VB VD − VB
⇒
I3 =
=
+



R
R
R
R6



3
1
4






V
−
V
V
−
V
V
−
V


D
B
C
B 
D



 A


+ I6 =
I4 =




R4
R3
R6






V
−
V


D
B


 I5 =

R6
La expresión de I6 no se ha desarrollado, pues por hipótesis es nula. Además, dado que I6 =
(VC − VD )/R5 = 0, y además R5 no es una resistencia infinita, se deduce que necesariamente
VC − VD = 0, es decir, VC = VD . Como la toma de tierra es el punto B, también se puede hacer
uso de la ecuación VB = 0. Por último, la fuente de tensión impone la ecuación VE − VB = V ,
que haciendo uso de VB = 0 queda en VE = V . Se tiene pues que el sistema de ecuaciones puede
simplificarse todavı́a más:

I6 = 0



VC = VD
V

B = 0


VE = V

VA − VD VD



=


R4

 R2
V − VA VD VD
⇒
=
+


R1
R4 R6





V − VD VD


 A
=
R3
R6




En lo que respecta al sistema, parece no ser tan complejo como inicialmente creı́amos. Vayamos
ahora poco a poco.
De la tercera ecuación se deduce:
VD = VA
R6
R3 + R6
(5.3)
Si esta expresión se sustituye en la segunda ecuación del sistema:
R4 + R6
R6
R4 + R6
V − VA
= VD
= VA
⇔
R1
R4 R6
R3 + R6
R4 R6
R1
R4 + R6
V = VA
+1 =
R3 + R6
R4
R4 (R3 + R6 )
VA
⇔
R1 (R4 + R6 ) + R4 (R3 + R6 )
R4 (R3 + R6 )
VA = V
R1 (R4 + R6 ) + R4 (R3 + R6 )
La expresión de VA obtenida puede sustituirse en la ecuación (5.3), para obtener ası́ una expresión de VD en la que no intervengan otras variables.
VD = V
R4 R6
R1 (R4 + R6 ) + R4 (R3 + R6 )
80
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Ahora simplifiquemos un poco la primera ecuación del sistema de ecuaciones original:
VD
VA − VD
=
⇔
R2
R4
VA
R2 + R4
⇔
= VD
R2
R2 R4
R2 + R4
VA = VD
R4
Si ahora sustituimos las expresiones de VA y VD en esta última ecuación, se obtiene:
!
✚
R
(R
+
R
)
4
3
6
✚
V
✭✭✭ =
✭✭✭
✭
✭
✭
R1 (R
+
R
)
+
R
(R
+
R6 )
4✭✭✭6
4
3
!
✭✭✭
✚
R2 + R4
R
R
✚4 6
V
✭✭ ⇔
✭✭✭✭
R4
✭
✭
R1 (R4✭+✭R
) + R4 (R3 + R6 )
✭6✭
✭✭✭
R6 (R2 + R4 )
⇔
R3 + R6 =
R4
R6✘R✘4 ⇔
R6✘R✘4 = R6 R2 + ✘
R3 R4 + ✘
R3 R4 = R6 R2
Que es la relación buscada, la cual deben cumplir las resistencias del circuito para que la
corriente que circula por la resistencia R5 sea nula (¡uf!).
Ejercicio 5.7: Se pide hallar el valor de la corriente que circula a través de la resistencia R
del circuito de la Figura 5.16 (R = 2000Ω).
2000Ω
2V
12V
2000Ω
R
Figura 5.16: Ejemplo 5.7
Solución
Se nos pide hallar la corriente que circula por la resistencia R. Como no nos han dado
ninguna toma de tierra en el enunciado, fijaremos una a nuestra conveniencia.
Otro detalle a tener en cuenta a la hora de resolver el ejercicio tiene que ver con el hecho
de que nos estén pidiendo obtener una corriente, la que circula por R. Para especificar una
corriente no basta dar su valor, sino también su sentido de circulación. Recordemos que, cuando
resolvemos un circuito, suponemos sentidos aleatorios para las corrientes de cada rama del
81
5.2. MÉTODO DE LOS NUDOS
C
12V
2000Ω
A
2V
I1
D
I2
I3
2000Ω
R
B
Figura 5.17: Ejemplo 5.7, corrientes asignadas a cada rama y toma de tierra emplazada
circuito. Los sentidos elegidos, como ya dijimos en su dı́a, no influyen en el resultado general,
más que en el signo de las corrientes obtenidas. Si una corriente se supone que circula de A a
B, y se resuelve el circuito, se obtiene un determinado valor de corriente I. Por contra, si se
supone que circula de B a A, y se resuelve el circuito, se obtendrı́a el valor −I. Por supuesto,
como es de esperar, ambas corrientes son la misma, pues tienen sentidos de circulación opuestos
y el mismo valor pero cambiado de signo; es decir, como habı́amos dicho con anterioridad, los
sentidos supuestos no influyen en la resolución del circuito. Ası́ pues, cuando se dé el resultado,
será importante especificar el sentido de circulación de la corriente. No es lo mismo decir una
corriente que circula hacia arriba, de 1A, que una corriente que circula hacia abajo, de 1A.
La Figura 5.17 muestra las corrientes supuestas y la toma de tierra colocada en un punto
elegido a nuestro gusto. Notar que la corriente que circula por la resistencia R, I2 , se ha supuesto
que circula hacia abajo.
Apliquemos el método de los nudos al nudo A, único nudo de interés del circuito:
I1 + I3 = I2
(Nudo A)
Tras aplicar la Ley de Ohm a las corrientes presentes en la ecuación del nudo A, se obtiene:


VC − VA 



I1 =






2000


VC − VA VB − VA VD − VB
VD − VB
⇒
+
=
I2 =


2000 
2000
2000
2000





V
−
V


B
A
 I3 =

2000
Por otro lado, la toma de tierra impone VA = 0. La fuente de tensión de 12V nos dice que
VC − VB = 12; la fuente de tensión de 2V nos dice que VA − VD = 2, que debido a la toma
de tierra se reduce en VD = −2. Si agrupamos estas ecuaciones con la ecuación del nudo A, se
tiene:


 VA = 0

12 + VB
VB
− 2 − VB
VD = −2
⇒
+
=


2000
2000
2000
VC − VB = 12
De donde se obtiene VB = −14/3.
La corriente I2 , la corriente que circula por R, se puede obtener mediante la expresión de
la Ley de Ohm:
−2 + 14/3
VD − VB
=
= 1,3̂mA
I2 =
2000
2000
Por tanto, por la resistencia R circula una corriente hacia abajo de 1,3̂mA. Equivalentemente,
se puede decir que por la resistencia R circula una corriente hacia arriba de −1,3̂mA.
82
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Ejercicio 5.8: Se pide hallar la resistencia equivalente, medida entre los terminales A y B,
del conjunto de resistencias de la Figura 5.18.
R1=1KΩ
R6=2KΩ R5=1KΩ
R2=2KΩ
A
R8=3KΩ
R7=2KΩ
R4=1KΩ
R3=1KΩ
B
R9=2KΩ
Figura 5.18: Ejemplo 5.8
Solución
No se trata éste de un ejercicio difı́cil. Lo importante de él son los detalles que se van
a recalcar, a los que ya se ha hecho referencia con anterioridad, pero que es posible que no
quedaran claros.
En primer lugar vamos a introducir una notación que simplifica la escritura de asociaciones.
Numéricamente, sabemos que la asociación en paralelo de dos resistencias, digamos R1 y R2 ,
viene dada por la fórmula:
1
1
1
=
+
Req
R1 R2
De donde es fácil deducir que:
R1 R2
R1 + R2
Pues bien, la asociación en paralelo puede expresarse también como:
Req =
Req = R1 ||R2
Por supuesto, esto es una soberana tonterı́a, sin más utilidad que la de simplificar la escritura del
concepto dos resistencias asociadas en paralelo. Ası́ pues, si quisiéramos hablar de la asociación
de dos resistencias Ri y Rj en paralelo, podrı́amos simplemente escribir Ri ||Rj en vez de la
fórmula que expresa el cálculo real del valor de Req .
Análogamente, nos podrı́amos preguntar si para las asociaciones en serie existe una manera
simplificada de representarlas. Lo cierto es que la fórmula de la resistencia equivalente de dos
resistencias asociadas en serie es tan elemental (suma de las resistencias), que para representar
dos resistencias R1 y R2 asociadas en serie, se suele usar la misma fórmula asociada al valor
numérico de la resistencia equivalente:
Req = R1 + R2
Resolvamos el ejercicio poco a poco. Por suerte en este ejemplo, todas las resistencias pueden
asociarse en serie y/o en paralelo entre sı́, de modo que todas las asociaciones pueden resolverse de forma trivial. Por tanto, nos limitaremos a localizar las asociaciones de tipo serie y
83
5.2. MÉTODO DE LOS NUDOS
R1=1KΩ
F
R6=2KΩ R5=1KΩ
E
R2=2KΩ
H
A
D
R8=3KΩ
R7=2KΩ
R4=1KΩ
R3=1KΩ
B
G
R9=2KΩ
C
Figura 5.19: Ejemplo 5.8 con ciertos puntos remarcados
F
Req2=3000Ω
Req1=1200Ω
E
1000Ω
Req3=2000/3Ω
H
A
1000Ω
B
G
2000Ω
C
Figura 5.20: Ejemplo 5.8 con algunas resistencias ya asociadas
paralelo existentes, para ir ası́ simplificando el circuito poco a poco, hasta llegar a la resistencia
equivalente buscada. Es importante no olvidar que nos están pidiendo la resistencia equivalente
medida entre los puntos A y B, y por tanto, dichos puntos no pueden ser eliminados durante
los procesos de asociación (recuérdese en este sentido, tal y como se explicó en la sección 4.4,
cómo asociar en serie o en paralelo suponı́a la eliminación de nodos y ramas respectivamete).
La Figura 5.19 muestra el circuito con ciertos puntos de interés remarcados.
Las primeras asociaciones que vamos a llevar a cabo son:
• R1 ||R2 : R1 y R2 están conectadas en paralelo, ya que sus terminales son comunes (puntos
E y H del circuito).
• R8 ||R7 : R8 y R7 están conectadas en paralelo, ya que sus terminales están conectados
entre sı́ (puntos F y G del circuito).
• R6 + R5 : R6 y R5 están conectadas en serie, dado que se sitúan en la misma rama (rama
F-D-E).
Tras asociar todas esas resistencias, el circuito se simplifica y queda como se muestra en la
Figura 5.20.
Los valores obtenidos de resistencias equivalentes se obtienen aplicando directamente las
fórmulas de las asociaciones en serie y en paralelo:
3000 · 2000
R8 R7
=
= 1200Ω
R8 + R7
3000 + 2000
Req2 = R6 + R5 = 2000 + 1000 = 3000Ω
R1 R2
1000 · 2000
2000
= R1 ||R2 =
=
=
Ω
R1 + R2
1000 + 2000
3
Req1 = R8 ||R7 =
Req3
84
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
E
Req4=6200Ω
Req3=2000/3Ω
1000Ω
H
A
1000Ω
B
C
Figura 5.21: Ejemplo 5.8, todavı́a más simplificado
E
Req3=2000/3Ω
Req5=7750/9Ω
H
A
1000Ω
B
C
Figura 5.22: Ejemplo 5.8, todavı́a más simplificado
En la Figura 5.20 se ha dibujado una flecha en trazo discontinuo, que engloba a tres resistencias, Req1 , Req2 y la de 2000Ω, que se encuentran conectadas en serie, ya que las tres
se sitúan en la misma rama. Por tanto, pueden asociarse en serie, quedando el circuito de la
Figura 5.21.
La resistencia R4 se ha obtenido como asociación en serie de las resistencias Req1 , Req2 y de
la de 2000Ω, dando lugar a:
Req4 = 1200 + 3000 + 2000 = 6200Ω
Las dos resistencias que son abarcadas por la flecha a trazos, a su vez, están asociadas en
paralelo, ya que sus terminales son comunes (puntos E y C). Por tanto, pueden asociarse en
paralelo, quedando el circuito de la Figura 5.22.
En la Figura 5.22 se puede apreciar la resistencia equivalente (Req5 ) resultado de asociar en
paralelo las resistencias Req4 y la de 1000Ω:
Req5 = Req4 ||1000 =
6200 · 1000
7750
=
Ω
6200 + 1000
9
En el circuito de la Figura 5.22 se puede apreciar que las resistencias Req5 y Req3 están conectadas en serie, ya que se sitúan sobre la misma rama. Por tanto, se pueden asociar en serie,
quedando el circuito de la Figura 5.23.
A
Req6=13750/9Ω
1000Ω
B
Figura 5.23: Ejemplo 5.8. Ya queda poco...
85
5.2. MÉTODO DE LOS NUDOS
A
Req=55000/91Ω
B
Figura 5.24: resistencia equivalente buscada
Donde la resistencia Req6 se obtiene como el serie de las resistencias Req5 y Req3 :
Req6 = Req5 + Req3 =
13750
7750 2000
+
=
Ω
9
3
9
Por último, queda asociar en paralelo las dos resistencias restantes, Req6 y la resistencia de
1000Ω. La resistencia equivalente es la mostrada en la Figura 5.24.
Es decir, el valor de la resistencia equivalente entre los terminales A y B del circuito original
es de:
55000
Ω ≈ 604,4Ω
Req =
91
Por tanto, todo el conjunto de resistencias mostrado en la Figura 5.18 puede sustituirse por
una resistencia de aproximadamente 604,4Ω, la cual muestra un comportamiento equivalente
todo el conjunto (es decir, cualquier circuito externo que se acoplase al conjunto original de
resistencias se comportarı́a de igual modo tanto con todas las resistencias como con la resistencia
equivalente).
En este ejercicio tiene especial importancia el procedimiento seguido a la hora de obtener
la resistencia equivalente que se nos pedı́a. A la hora de asociar elementos, ya no solamente
resistencias, puede resultar tentador asociar como se nos pase por la cabeza, por ejemplo,
buscando hacer pocos cálculos. Sin embargo, es aconsejable mantener siempre en mente qué se
quiere realmente, y si las asociaciones que se están realizando son siquiera posibles.
Tal y como se comentó en la sección 4.4, las asociaciones en serie suponen la destrucción
de los nodos intermedios a los elementos asociados. Por ejemplo, al asociar las resistencias R5
y R6 , el nudo D dejó de existir (ver cómo en la Figura 5.20 dicho punto ya no aparece). Por
tanto, a partir de entonces, cualquier dato referente al nodo D no podrı́a haberse calculado (la
tensión en el nodo D no tendrı́a sentido ya que el nodo D habrı́a dejado de existir. Por tanto, ese
modelo simplificado de la Figura 5.20 y subsiguientes no podrı́a usarse para calcular la tensión
en D).
Este detalle es muy importante, dado que durante el proceso de asociación de resistencias,
podrı́amos haber eliminado a los puntos A y B, lo cual habrı́a sido un error, ya que se nos pedı́a
concretamente la resistencia equivalente entre los puntos A y B. Por ejemplo, en el circuito de
la Figura 5.22 nos habrı́amos podido sentir tentados asociar en serie las resistencias Req3 y la
de 1000Ω, lo cual habrı́a supuesto la desaparición del punto A, y por tanto no se podrı́a haber
obtenido la resistencia equivalente buscada.
Ejercicio 5.9: Calcular el valor de la tension en el nudo A en el circuito de la Figura 5.25.
Suponer que R1 = R2 = R3 = R4 = R5 = 1000Ω, que L1 = L2 = 1,5mH y que C = 4nF .
Solución
El circuito de la Figura 5.25 presenta tanto condensadores como bobinas. Sabemos que en
condiciones de corriente continua (en las cuales estamos, dado que la única fuente presente en
86
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
R1
C
R2
10V
A
R3
R4
L1
R5
L2
Figura 5.25: Ejemplo 5.9
B
R1
R2
10V
A
R4
E
R5
I1
C
R3
I2
D
Figura 5.26: Ejemplo 5.9, sin bobinas ni condensadores, y con corrientes asignadas
el circuito es una fuente de tensión continua), ambos se simplifican. Concretamente, un condensador, en corriente continua, se transforma en un circuito abierto; una bobina, en corriente
continua, muestra un comportamiento equivalente al de un cortocircuito, y por tanto puede
sustituirse por tal. De este modo, antes de ir más lejos, sustituiremos dichos elementos por
sus respectivos equivalentes en corriente continua. El resultado es el circuito de la Figura 5.26,
donde además se han supuesto las corrientes necesarias en cada rama para la obtención de la
tensión en A según el método de los nudos (recuérdese que los sentidos de circulación de cada
corriente son asignados a gusto de uno mismo).
En la Figura 5.26 se puede apreciar cómo el condensador ha sido sustituido por un circuito
abierto, y las dos bobinas, por un cortocircuito cada una. Puede que resulte raro cómo se han
supuesto las corrientes en cada rama de este circuito. La corriente de la rama A-B-C-D, I1 ,
sigue dentro de lo normal. Por contra, en la rama de la resistencia R4 se ha supuesto circular la
misma corriente, I2 , que en la rama D-E-A. ¿No deberı́amos haber supuesto que en la rama de
R4 circula otra corriente distinta, digamos I3 ? La respuesta es que sı́, que podrı́amos haberlo
hecho. Sin embargo, y por suerte para nosotros, millones de años de evolución dieron a la especie
humana la capacidad de pensar, no con el ojo del culo, sino con la cabeza que tienen encima
de los hombros (en el caso de los varones, susodicha capacidad se reparte a partes iguales entre
lo que hay encima de los hombros y lo que hay debajo del ombligo). Pensemos un poco.
Sabemos que en la rama A-B-C-D hay un circuito abierto (el dejado por el condensador).
Sabemos que por un circuito abierto no puede circular corriente alguna (sección 2.1). Por tanto,
la corriente I1 , que es la que circula a través de dicho circuito abierto (y a su vez a través de
toda la rama A-B-C-D; recordemos que en una rama existe una única corriente), ha de ser nula,
es decir, I1 = 0.
Sabiendo que I1 = 0, es evidente que toda la corriente que llega al nudo A a través de R3
(rama D-E-A), I2 , ha de desviarse hacia abajo, por la resistencia R4 , y de ahı́ que la corriente
I2 se haya dibujado abarcando R3 , R4 y R5 . Analı́ticamente se podrı́a haber llegado a la misma
conclusión. Si hubiéramos supuesto que al nudo A entra una corriente I2 ,(corriente que viene de
87
5.2. MÉTODO DE LOS NUDOS
R3 ), y que salen dos corrientes, I1 e I3 (esta última serı́a la que circuları́a por R4 ), podrı́amos
haber planteado la ecuación:
I2 = I1 + I3
Que al ser I1 = 0 se habrı́a quedado en I2 = I3 , tal y como hemos reflejado en la Figura 5.26.
Digamos que, de algún modo, nos podemos olvidar de toda la zona izquierda del circuito
(aquella zona abarcada por I1 ). Podemos aplicar la ley de los nudos a los nudos A, E y D. En
cada uno de esos nudos, existe una única corriente que entra y una única que sale, I2 , ya que
son nudos situados en la misma rama. Aplicar en este caso la ley de los nudos no viene a ser
otra cosa que igualar las distintas expresiones que, según la Ley de Ohm, puede adoptar I2 .
Según la Ley de Ohm:
VE − VA
R3
VA − VD
I2 =
R4
VD − VE
I2 =
R5
I2 =
Sabiendo que, además, todas las resistencias tienen el mismo valor:
VE − VA = VA − VD = VD − VE
Como además la toma de tierra está cortocircuitada con el punto D, la ecuación anterior se
simplifica todavı́a más:
VE − VA = VA = −VE
La igualdad anterior conforma un sistema de dos ecuaciones con dos incógnitas:
(
VE − VA = VA
VA = −VE
De donde es fácil obtener que:
VA = VE = 0V
Ejercicio 5.10: Determinar las potencias generadas o consumidas por los generadores del
circuito de la Figura 5.27.
1KΩ
30V
+
−
1KΩ
10V
+
−
1KΩ
20V
+
−
Figura 5.27: Ejemplo 5.10
Solución
1KΩ
1KΩ
88
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
I1
10V
+
−
1KΩ
A
H
30V
I3
I2
20V
D
+
−
C
1KΩ
+
−
E
G
B
I4
I5
1KΩ
1KΩ
F
Figura 5.28: Ejemplo 5.10, corrientes asignadas a cada rama
Para resolver el circuito, en primer lugar, supondremos la presencia de una toma de tierra en
un lugar fijado por nosotros. Como de costumbre, fijaremos la toma de tierra abajo. Además,
supondremos corrientes de sentidos aleatorios en cada rama del circuito para ası́ resolverlo
mediante el método de los nudos (Figura 5.28).
Apliquemos el método de los nudos a los nudos A y B:
I1 + I3 = I2
I5 = I3 + I4
Apliquemos ahora la ley
solamente a tensiones.


 I =

1







I2 =




I3 =







I4 =






 I5 =
(Nudo A)
(Nudo B)
de Ohm para sustituir cada corriente por expresiones que engloben
VC − VA
1000
VA − VE
1000
VD − VA
1000
VB − VF
1000
VF − VB
1000
















V − VA VD − VA VA − VE

 C
+
=
1000
1000
1000
⇒
V
−
V
V
− VF
V
−
V


D
A
B
F
B



=
+


1000
1000
1000









Consideremos ahora la información aportada por las fuentes de tensión ası́ como por la toma de
tierra. La toma de tierra nos dice que VG = VH = VF = 0, ya que G, H y F son puntos que están
cortocircuitados con la toma de tierra. La fuente de tensión de 10V implica que VC − VH = 10,
la de 20V , VE − VG = 20, y la de 30V , VD − VB = 30. Si consideramos la toma de tierra,
esas ecuaciones se reducen a VC = 10, VE = 20 y VD − VB = 30 (la última ecuación no se ve
alterada).
El sistema de ecuaciones original puede simplificarse aplicando estas últimas ecuaciones:



VC = 10


10 − VA VD − VA VA − 20






+
=
VE = 20
1000
1000
1000
⇒
0
−
V
+
30
V
−
V
=
30
V
−
V
VD − 30 − 0



D
D
B
D
A





=
+
VF = 0
1000
1000
1000
Sistema de dos ecuaciones con dos incógnitas del que se deduce fácilmente:
VA = 18,75V, VD = 26,25V
Para obtener las potencias generadas o consumidas por las fuentes de tensión, se hará uso de
la ecuación ((1.3)), y por tanto habrá que obtener los valores de las corrientes que atraviesan a
5.2. MÉTODO DE LOS NUDOS
89
dichas fuentes de tensión, I1 , I2 e I3 .
VC − VA
10 − 18,75
=
= −8,75 · 10−3
1000
1000
18,75 − 20
VA − VE
=
= −1,25 · 10−3
I2 =
1000
1000
VD − VA
26,25 − 18,75
I3 =
=
= 7,5 · 10−3
1000
1000
I1 =
La ecuación ((1.3)) nos dice que si una corriente IAB que circula de un punto A a otro punto B
atraviesa una diferencia de tensión VAB , entonces la potencia generada o consumida es IAB VAB .
Apliquémoslo a cada una de las fuentes del circuito:
• Fuente de tensión de 10V : la corriente I1 atraviesa a la fuente desde su polo negativo a su
polo positivo (desde H a C). Por tanto, la diferencia de tensión que se debe tomar es VHC .
Según la misma fuente de tensión, VC − VH = 10, y por tanto VHC = VH − VC = −10. Se
tiene que la potencia en esa fuente es de:
P10V = −8,75 · 10−3 (−10) = 0,0875W
Que al ser potencia positiva, se considera potencia consumida, es decir, la fuente de tensión
de 10V absorbe energı́a del resto del circuito.
• Fuente de tensión de 20V : la corriente I2 atraviesa a la fuente desde su polo positivo a
su polo negativo (desde E a G). Por tanto, la diferencia de tensión que se debe tomar es
VEG . Según la misma fuente de tensión, VEG = VE − VG = 20. Se tiene que la potencia en
esa fuente es de:
P20V = −1,25 · 10−3 · 20 = −0,025W
Que al ser potencia negativa, se considera potencia generada, es decir, la fuente de tensión
de 20V genera energı́a que es utilizada (consumida) por otros elementos del circuito.
• Fuente de tensión de 30V : la corriente I3 atraviesa a la fuente desde su polo negativo a su
polo positivo (desde B a D). Por tanto, la diferencia de tensión que se debe tomar es VBD .
Según la misma fuente de tensión, VD − VB = 30, y por tanto VBD = VB − VD = −30. Se
tiene que la potencia en esa fuente es de:
P30V = 7,5 · 10−3 (−30) = −0,225W
Que al ser potencia negativa, se considera potencia generada, es decir, la fuente de tensión
de 30V genera energı́a que es utilizada (consumida) por otros elementos del circuito.
Ejercicio 5.11: Para el circuito de la Figura 5.29, se pide obtener el valor de la constante a,
sabiendo que la máxima corriente que puede circular por la bobina es de 2A. Tomar L = 2H.
Suponer que la tensión que impone la fuente de tensión sigue la función:


0 si t < 0
V (t) = t si 0 ≤ t < a


0 si t ≥ a
Solución
90
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
V(t)
L
Figura 5.29: Ejemplo 5.11
A
V(t)
I(t)
L
B
Figura 5.30: Ejemplo 5.11
Este ejercicio tiene que ver realmente poco con el método de los nudos. Se trata de un
sencillo ejercicio en el que no basta aplicar el mecánico procedimiento de resolución de ejercicios mediante la ley de los nudos, sino que requiere pensar un poco más de a lo que estamos
acostumbrados.
El circuito de la Figura 5.29 consta de una fuente de tensión variable en el tiempo y de una
bobina de valor L. La forma de la tensión que impone la fuente de tensión viene dada por la
función V (t), que es fundamentalmente la función identidad, pero acotada a un cierto intervalo:
antes del instante 0, la función vale 0. De 0 al instante a, la función es la identidad. De a en
adelante, la función vale igualmente 0.
Debemos recordar la ecuación que rige el comportamiento de una bobina. Si una bobina
de inductancia L es atravesada por una corriente IAB (t) desde su extremo A a su extremo B,
entonces la diferencia de tensión VAB (t) que hay entre sus extremos viene dada por la ecuación
(2.4), a saber:
dIAB (t)
VAB (t) = L
dt
En nuestro ejemplo, tal y como se representa en la Figura 5.30, se ha supuesto que la corriente
que atraviesa a la bobina circula de A a B (como siempre, podrı́a haberse supuesto que la
corriente circulaba justamente en el otro sentido, de B a A). Dicha corriente se ha denominado
I(t). Dado ese sentido de circulación de la corriente, se tiene que la diferencia de tensión que
aparece en la ecuación (2.4) es justamente VAB (t), que coincide con la tensión impuesta por la
fuente de tensión, V (t).
La ecuación que rige el circuito actual vendrá dada, por tanto, por:
V (t) = L
dI
dt
¿Qué hacer con esta ecuación? Pensando un poco, debemos ser capaces de darnos cuenta de
que podemos obtener el valor de I(t) de esa ecuación diferencial, ya que se conoce el valor de
la función V (t).
91
5.2. MÉTODO DE LOS NUDOS
Operemos un poco:
V (t) = L
dI
⇔
dt
1
V (t)dt = dI ⇔
L
Z t
Z I(t)
1
V (τ )dτ =
dI ⇔
L 0
I(0)
Z
1 t
V (τ )dτ = I(t) − I(0)
L 0
En este ejemplo, I(0) = 0 por hipótesis. Esto es ası́ ya que hasta el instante 0 (es decir, desde
−∞ hasta 0 inclusive) la fuente de tensión no inyecta tensión alguna (su valor es 0), y por
tanto no puede haber corriente alguna hasta el instante 0, incluido éste. Como además V (τ ) es
una recta de pendiente 1 desde 0 hasta el instante a, la ecuación anterior puede desarrollarse
para valores de tiempo entre 0 y a del siguiente modo:
Z
1 t
V (τ )dτ = I(t) − I(0) ⇔
L 0
Z
1 t
τ dτ = I(t) ⇔
L 0
t2
I(t) =
2L
Expresión válida sólo para instantes de tiempo t comprendidos entre 0 y a.
Como esta corriente depende de forma directa del instante de tiempo t (es directamente
proporcional al cuadrado de t), su valor máximo se alcanzará justamente en el instante a, ya
que dicho instante es el último en el que es válida la ecuación obtenida. Por tanto, en t = a
debe cumplirse que I(t) sea igual a 2A, que es lo que nos decı́a el enunciado:
I(a) = 2 ⇔
a2
=2⇔
2L √
a= 8
Donde se ha usado que el valor de L es de 2H.
Ejercicio 5.12: Se pide hallar la resistencia equivalente, medida entre las terminales A y B,
del circuito de la Figura 5.31.
Solución
El conjunto de resistencias del que se nos pide hallar la resistencia equivalente muestra una
configuración que no puede ser simplificada mediante simples asociaciones en serie y en paralelo.
Si bien hay un par de resistencias (las dos de 1KΩ de arriba a la derecha) que inicialmente
pueden asociarse en serie, a partir de ahı́ no se puede realizar más asociaciones en serie o
en paralelo. Para obtener la resistencia equivalente entre A y B, por tanto, se debe recurrir
92
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
A
3KΩ
1KΩ
1KΩ
2KΩ
2KΩ
1KΩ
1KΩ
B
Figura 5.31: Ejemplo 5.12
A
3KΩ
1KΩ
A
1KΩ
2KΩ
2KΩ
Req
1KΩ
B
B
1KΩ
Figura 5.32: equivalencia buscada
al método genérico para la obtención de elementos equivalentes, tal y como se explicó en la
sección 4.4.
Se procederá del siguiente modo: se aplicará al conjunto de resistencias una determinada
tensión entre los terminales A y B; se obtendrá, aplicada esa tensión, la corriente de entrada (o
de salida, pues son la misma), del conjunto de resistencias, digamos Iin1 . Después se aplicará el
mismo procedimiento al supuesto circuito equivalente, para obtener ası́ la corriente de entrada
(o de salida) en tal, digamos Iin2 . La equivalencia buscada se representa en la Figura 5.32.
Para resolver el ejercicio se va a proceder inicialmente a obtener la expresión de la corriente
de entrada en el conjunto de resistencias original, aplicada una tensión V a los terminales A
y B. Como el circuito se va a resolver mediante el método de los nudos, también se van a
suponer corrientes en cada una de las ramas; además, para agilizar la resolución del circuito,
se colocará una toma de tierra (abajo, como estamos acostumbrados), y se señalarán una serie
de puntos de interés. Todo ello se representa en la Figura 5.33.
Apliquemos el método de los nudos a los nudos C, D y E:
Iin1 = I1 + I2
I1 + I5 = I3
I2 = I5 + I4
(Nudo C)
(Nudo D)
(Nudo E)
93
5.2. MÉTODO DE LOS NUDOS
3KΩ
A
1KΩ
C
Iin1
I2
1KΩ
+
−
V
I1
2KΩ
2KΩ
D
E
I5
1KΩ
F
B
I3
I4
1KΩ
Figura 5.33: obtención de la corriente de entrada, modelo original
Si hacemos uso de la Ley de Ohm, las ecuaciones se reducen a:


VA −VC
I
=


in1
3000






V
−
V

C
D 




I
1 =





1000


VC − VD VC − VE
VA − VC






V
−
V
=
+
C
E








1000
2000
 3000

 I2 = 2000 
VC − VD VE − VD VD − VF
⇒
VD − VF
+
=



I3 =
1000
2000
1000






1000 


V
−
V
V
− VF
V
−
V



E
D
E
C
E


VE − VF 


=
+




I4 =
2000
2000
1000



1000 





V − VD 



 I5 = E
2000
La toma de tierra nos dice que VB = VF = 0; además, según la fuente de tensión, VA − VB = V ,
lo que junto con la ecuación de la toma de tierra nos lleva a VA = V . Con estas ecuaciones el
sistema puede simplificarse:

V − VC
VC − VD VC − VE


=
+



1000
2000
 3000
VF = 0
VC − VD VE − VD VD − 0
⇒
+
=
VA = V

1000
2000
1000



V
−
V
V
−
V
V

C
E
E
D
E −0

=
+
2000
2000
1000
Sistema de ecuaciones del cual se obtiene:
VC =
7
9
19
V, VE = V, VD = V
67
67
67
Y por tanto, la corriente de entrada Iin1 del circuito original ante una entrada V es:
19
1
2
VA − VC
= V − V ·
=
V
Iin1 =
3000
67
3000
8375
En el modelo equivalente es trivial seguir este procedimiento para la obtención de la corriente
de entrada Iin2 ante una tensión de entrada V . La figura 5.34 muestra el escenario en cuestión.
En ese circuito es evidente que la corriente de entrada Iin2 toma el valor:
Iin2 =
VA − VB
V
=
Req
Req
94
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
A
Iin2
V
Req
B
Figura 5.34: obtención de la corriente de entrada, modelo simplificado
Dado directamente por la Ley de Ohm.
Para que ambos modelos sean equivalentes, ante una misma tensión de entrada (V ), las
corrientes de entrada (Iin1 e Iin2 ) deben ser iguales. Por tanto, nos resta imponer la igualdad
entre ambas corrientes de entrada para obtener el valor de la resistencia equivalente:
Iin1 = Iin2 ⇔
1
2
V ⇔
V =
8375
Req
Req = 4187,5Ω
Que es el valor de la resistencia equivalente buscada: el conjunto original de resistencias, visto
desde los terminales A y B, muestra el mismo comportamiento que una resistencia de 4187,5Ω.
5.3.
Método de las mallas
El método de las mallas es el otro gran método de resolución de circuitos que estudiaremos.
Junto con el método de los nudos, forman el gran pilar de la resolución de circuitos de todo
tipo, ya sean de corriente continua o no.
El método de las mallas está basado directamente en la ley de las mallas (sección 3.3), pero
empleada de un modo que aumenta la eficiencia del método en gran medida. Los pasos básicos
del método son los siguientes:
• Definición de las corrientes de malla: dado un circuito, se deben definir corrientes de
malla. Una corriente de malla se define para cada malla del circuito que sea indivisible
en otras, de tal modo que se le asigna un valor en forma de incógnita (Ii ), ası́ como un
sentido de circulación, horario o antihorario. Una corriente de malla es, por tanto, una
corriente que está asociada a una malla del circuito, y que consta de un valor y un sentido
de circulación. Realmente no es necesario elegir mallas indivisibles en otras a la hora de
aplicar el método; sin embargo, se recomienda que ası́ se haga, pues redunda en una mayor
facilidad de resolución. Nótese también que, como de costumbre, el sentido de circulación
supuesto a cada corriente de malla depende totalmente de nosotros, pudiéndose elegir de
forma indistinta tanto el sentido horario como el antihorario. Supongamos el circuito de
la Figura 5.35, sobre el que se han definido corrientes de malla. Las corrientes de malla
definidas en este ejemplo son I1 , I2 , I3 e I4 . La corriente I1 es la corriente asignada a
la malla A-C-D-B, y tiene sentido horario; la corriente I2 es la asignada a la malla CE-F-D, y tiene sentido antihorario; la corriente I3 es la asignada a la malla E-I-J-F, y
tiene sentido antihorario; la corriente I4 es la asignada a la malla G-H-I-E, y tiene sentido
horario. Notar cómo cada corriente se dibuja recorriendo todo el perı́metro de la malla a
la que está asignada.
95
5.3. MÉTODO DE LAS MALLAS
V2
R6
H
+
−
G
I4
A
C
R2
E
I
R5
+
V1 −
B
I1
R1 I2
R4
R7
I3
D
R3
F
J
Figura 5.35: un circuito al que aplicar el método de las mallas
• Obtención de las ecuaciones de malla: el siguiente paso consiste en obtener tantas
ecuaciones de malla como mallas con corrientes de malla se hayan definido. En el ejemplo
de la Figura 5.35 deberı́amos definir 4 ecuaciones de malla, ya que hay 4 mallas con
corrientes de malla definidas. Cada ecuación de malla tiene dos miembros:
1. Corriente de la malla en cuestión, multiplicada por la suma de todas las resistencias
presentes en la malla. Si hay alguna rama que contiene resistencias y que es colindante
a otra malla (en nuestro ejemplo, la rama de R1 ,la de R4 y la de R5 ), se añaden más
sumandos a este miembro de la ecuación:
a) Si la rama común a las dos mallas es una tal que la corriente de la malla vecina
(no la de la malla que estamos tratando) tiene un sentido que coincide con el
de nuestra corriente de malla en la resistencia común a ambas mallas, entonces
se suma el producto de la corriente de malla vecina por la resistencia común.
Un ejemplo de esta situación serı́a la rama de R1 , donde I1 e I2 coinciden en
la resistencia R1 con un mismo sentido, hacia abajo. Otro ejemplo de esta
situación serı́a la rama de R5 , donde I3 e I4 coinciden en la resistenciacon un
mismo sentido, hacia la izquierda. Por supuesto, si la rama común tuviera
más de una resistencia, este procedimiento se aplicarı́a a todas las resistencias
de la rama.
b) Si por contra, la rama común a las dos mallas es una tal que la corriente de la
malla vecina (no la de la malla que estamos tratando) tiene un sentido opuesto al
de nuestra corriente de malla en la resistencia común a ambas mallas, entonces
se resta el producto de la corriente de malla vecina por la resistencia común. Un
ejemplo de esta situación serı́a la rama de R4 , donde I2 llega a la resistencia con
sentido hacia arriba, mientras que I3 llega a la resistencia con sentido hacia
abajo. Por supuesto, si la rama común tuviera más de una resistencia, este
procedimiento se aplicarı́a a todas las resistencias de la rama.
2. El otro miembro de la ecuación es la suma de todos los generadores de tensión
presentes en la malla que se está analizando, de modo que suman (es decir, su valor
no se ve alterado en el signo) si y sólo si la corriente de malla atraviesa al generador
desde su polo negativo a su polo positivo, y restan (es decir, su valor se ve cambiado
de signo) si y sólo si la corriente de malla atraviesa al generador de su polo positivo
a su polo negativo. Si no hay ninguna fuente de tensión, la suma valdrı́a 0.
En el ejemplo que nos traemos entre manos habrı́a cuatro ecuaciones de malla, a
saber:
96
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
• Malla A-C-D-B: I1 R1 + I2 R1 = V1 . Nótese cómo en esta malla el valor de la
fuente de tensión no está cambiado de signo (suma). Esto se debe a que la
corriente de malla actual, I1 , atraviesa la fuente de tensión de su polo negativo
a su polo positivo. Nótese además la presencia de una rama compartida (rama
de R1 ), que introduce un término más a la ecuación.
• Malla C-E-F-D: I2 (R1 + R2 + R3 + R4 ) + I1 R1 − I3 R4 = 0. Nótese cómo en esta
malla hay dos ramas que están compartidas con otras mallas (las ramas de R1
y R4 ), y por tanto debe tenerse en consideración a ambas. Como en la rama de
R1 la corriente de malla vecina (I1 ) coincide en sentido de circulación con la
corriente de malla actual (I2 ), entonces I1 suma. En cambio, en la rama de R4
la corriente de malla vecina (I3 ) tiene sentido opuesto de circulación al de la
corriente de malla actual (I2 ), y de ahı́ que I3 reste. Nótese también como, al
no haber ningún generador de tensión en la malla actual, uno de los miembros
de la ecuación es 0.
• Malla E-I-J-F: I3 (R4 + R5 + R7 ) − I2 R4 + I4 R5 = 0. Nótese cómo en esta malla
hay dos ramas que están compartidas con otras mallas (las ramas de R4 y R5 ),
y por tanto debe tenerse en consideración a ambas. Como en la rama de R4
la corriente de malla vecina (I2 ) tiene sentido opuesto de circulación al de la
corriente de malla actual (I3 ), entonces I2 resta. En cambio, en la rama de
R5 la corriente de malla vecina (I4 ) coincide en sentido de circulación con la
corriente de malla actual (I3 ), y de ahı́ que I4 sume. Nótese también como, al
no haber ningún generador de tensión en la malla actual, uno de los miembros
de la ecuación es 0.
• Malla E-G-H-I: I4 (R6 + R5 ) + I3 R5 = −V2 . Nótese cómo en esta malla el valor
de la fuente de tensión está cambiado de signo (resta). Esto se debe a que la
corriente de malla actual, I4 , atraviesa la fuente de tensión de su polo positivo
a su polo negativo. Nótese además la presencia de una rama compartida (rama
de R5 ), que introduce un término más a la ecuación.
• Resolución: finalmente, se resuelve el sistema de ecuaciones formado por las ecuaciones
de malla obtenidas en el paso anterior. Las ecuaciones de malla son ecuaciones cuyas
incógnitas son las llamadas corrientes de malla. En nuestro ejemplo, esas corrientes son
I1 , I2 , I3 e I4 . Las corrientes de malla, como antes se dijo, son corrientes asociadas a mallas
del circuito. La cuestión es, ¿qué representan realmente esas corrientes? Las corrientes de
malla son corrientes secundarias que nos permiten obtener las corrientes que realmente
circulan por cada una de las ramas del circuito. Se podrı́a decir que las corrientes de
malla no existen realmente como tales, sino que son un formalismo inventado para poder
obtener, en base a ellas, las corrientes reales que circulan por las distintas ramas del
circuito. Necesitamos pues un método para, dadas las corrientes de malla, obtener las
corrientes reales del circuito. El método que vamos a proponer consta de dos posibles
casos:
1. El caso simple se da cuando se desea hallar la corriente que circula por una rama del
circuito, y la cual no es compartida por varias mallas. Por ejemplo, las ramas C-E y
D-F (ramas de las resistencias R2 y R3 respectivamente) no son ramas compartidas.
En este caso, la corriente que circula por dicha rama coincide con la única corriente
de malla que la barre. Ası́, en la resistencias R2 y R3 circuları́a una corriente igual
a I2 , ya que dicha corriente de malla es la única que logra barrer esas resistencias.
Por tanto, por I2 circuları́a una corriente de valor I2 y hacia la izquierda, mientras
que por R3 circuları́a una corriente de valor I2 y hacia la derecha. Igualmente, por
97
5.3. MÉTODO DE LAS MALLAS
R7 circuları́a una corriente de valor I3 y hacia arriba, ya que la rama donde se
sitúa R7 no es compartida, y la única corriente de malla que logra alcanzar a dicha
resistencia es I3 . Por último, por R6 circuları́a una corriente de valor I4 y hacia la
derecha, ya que la rama de R6 no es una rama compartida por varias mallas, y la
única corriente de malla que logra barrerla es I4 . Nótese como en todos estos casos se
podrı́a haber supuesto que la corriente que circula por cada resistencia tiene un valor
de signo opuesto y de sentido de circulación contrario al de la corriente de malla.
Por ejemplo, se podrı́a haber dicho igualmente que por R6 circula una corriente de
valor −I4 y hacia la izquierda, en vez de otra de valor I4 y hacia la derecha (ambas
corrientes son equivalentes, luego usar una u otra alternativa serı́a indiferente).
2. El caso no tan simple se da cuando se desea hallar la corriente que circula por una
rama del circuito que es común a varias de las mallas para las que se han definido
corrientes de malla. En el ejemplo actual, este caso se da, por ejemplo, en la rama
C-D (corriente que circula por R1 ) y en la rama E-F (corriente que circula por R4 ).
El método consiste en suponer que por la rama compartida circula una determinada
corriente, de valor I desconocido y de sentido de circulación elegido aleatoriamente
por nosotros. La corriente que circula por dicha rama es una corriente cuyo sentido
de circulación es el elegido por nosotros y cuyo valor, I, es igual a la suma de todas
las corrientes de malla que atraviesan la rama con sentido coincidente con el de I,
menos cada corriente de malla que atraviesa la rama con sentido opuesto al de I.
Tomemos como ejemplo la rama E-F, la de R4 . Podemos suponer que la corriente
que circula por dicha rama circula hacia abajo. En ese caso, el valor de la corriente
IR4 , es igual a IR4 = I3 − I2 : I3 suma (no se le cambia el signo), porque su sentido de
circulación al llegar a R4 es hacia abajo, coincidiendo ası́ con el sentido supuesto
a la corriente IR4 . Sin embargo, I2 resta (se le cambia el signo), porque su sentido
de circulación al llegar a R4 es hacia arriba, no coincidiendo ası́ con el sentido
supuesto a la corriente IR4 . Si hubiéramos supuesto que IR4 circulase hacia arriba,
entonces su valor numérico habrı́a sido IR4 = I2 − I3 , ya que en ese caso I2 habrı́a
coincidido con el sentido supuesto para IR4 , mientras que I3 no (esta corriente, de
todos modos, es equivalente a la otra, ya que sus valores numéricos son iguales pero
con signos contrarios, y sus sentidos de circulación son opuestos). Supongamos que
en nuestro ejemplo, los valores de todas las resistencias son de 1000Ω, y que además
V1 = 5V y V2 = 7V . El sistema de las ecuaciones de malla queda en:

1000I1 + 1000I2 = 5



1000I + 4000I − 1000I = 0
1
2
3

−1000I2 + 3000I3 + 1000I4 = 0



1000I3 + 2000I4 = −7
De donde se obtiene:
I1 =
83
−9
11
−51
,I2 =
,I3 =
,I4 =
13000
6500
13000
13000
Que son los valores de las corrientes de malla. Usando estos valores se puede obtener
los valores de las corrientes que circulan por las ramas del circuito, empleando para
ello el método explicado.
• IR1 : si suponemos que la corriente que circula por la rama de la resistencia R1
(rama compartida) circula hacia arriba, entonces su valor es:
IR1 = −I1 − I2 =
9
−83
+
= −5 · 10−3 A
13000 6500
98
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
• IR4 : si suponemos que la corriente que circula por la rama de la resistencia R4
(rama compartida) circula hacia abajo, entonces su valor es:
IR4 = I3 − I2 =
11
9
29
+
=
≈ 2,23 · 10−3 A
13000 6500
13000
• IR5 : si suponemos que la corriente que circula por la rama de la resistencia R5
(rama compartida) circula hacia la izquierda, entonces su valor es:
IR5 = I4 + I3 =
11
−1
−51
+
=
≈ −3,08 · 10−3A
13000 13000
325
• IR2 : la corriente que atraviesa la rama de la resistencia IR2 (rama no compartida) coincide con la corriente de malla I2 , y por tanto puede verse como una
corriente que circula hacia la izquierda y de valor:
−9
≈ −1,38 · 10−3 A
6500
IR2 = I2 =
• IR3 : la corriente que atraviesa la rama de la resistencia R3 (rama no compartida)
coincide con la corriente de malla I2 , y por tanto puede verse como una corriente
que circula hacia la derecha y de valor:
−9
≈ −1,38 · 10−3 A
6500
IR3 = I2 =
• IR7 : la corriente que atraviesa la rama de la resistencia IR7 (rama no compartida) coincide con la corriente de malla I3 , y por tanto puede verse como una
corriente que circula hacia arriba y de valor:
IR7 = I3 =
11
≈ 8,46 · 10−3 A
13000
• IR6 : la corriente que atraviesa la rama de la resistencia R6 (rama no compartida)
coincide con la corriente de malla I4 , y por tanto puede verse como una corriente
que circula hacia la derecha y de valor:
IR6 = I4 =
5.3.1.
−51
≈ −3,92 · 10−3A
13000
Método de las mallas con fuentes de corriente
Cuando se intenta resolver un circuito que contiene fuentes de corriente mediante el método
de las mallas, surge un problema. En una fuente de corriente existe una determinada tensión
entre sus bornes, que viene impuesta por el resto del circuito: es el caso análogo de una fuente
de tensión, que es atravesada por una determinada corriente impuesta por el resto del circuito.
La tensión que soporta una fuente de corriente es desconocida para nosotros, de modo que ésta
se transforma en una nueva incógnita que debe ser tenida en cuenta. El método de las mallas
considera las diferencias de tensión presentes a lo largo de una malla determinada, y por tanto,
la diferencia de tensión presente entre los terminales de una fuente de corriente también deberı́a
ser tenida en cuenta. Ası́ pues, la diferencia de tensión existente entre los terminales de una
fuente de corriente se convierte en otra incógnita del sistema de ecuaciones de malla del método
de las mallas.
Para cada fuente de corriente, por tanto, se le debe asignar una incógnita, digamos Vg ,
que representa la diferencia de tensión existente entre sus extremos. Además, para que dicha
tensión Vg tenga sentido, a la fuente de corriente se le debe asignar una polaridad (polo positivo
99
5.3. MÉTODO DE LAS MALLAS
1KΩ
1KΩ
1KΩ
10mA
+
− 5V
5mA
Figura 5.36: ejemplo del método de las mallas con fuentes de corriente
1KΩ
1KΩ
V1
I1 V2
C
-
A
5mA
1KΩ
+
10mA
+
− 5V
-
+
D
I2
B
Figura 5.37: ejemplo del método de las mallas con fuentes de corriente
y negativo), tal y como si fuera una fuente de tensión. Esa polaridad puede ser asignada de
forma aleatoria (¿por qué todo se puede asignar de forma aleatoria en Teorı́a de Circuitos?), de
modo que, en base a esa polaridad asignada, la fuente de corriente mostrará un comportamiento
análogo al de una fuente de tensión: la diferencia de tensión entre el polo positivo (elegido por
nosotros) y el negativo (también elegido por nosotros), es igual al valor de tensión supuesto, la
incógnita Vg .
A la hora de obtener las ecuaciones de malla, las fuentes de corriente se comportarán como
fuentes de tensión de valor incógnita desconocida (Vg ) y cuya polaridad es la que les hayamos
asignado. El problema en este tipo de situaciones es que, para resolver el sistema de ecuaciones,
las ecuaciones de malla se vuelven insuficientes: cada fuente de corriente introduce una nueva
incógnita, pero el número de ecuaciones de malla se mantiene constante, de modo que hay más
incógnitas que ecuaciones, y el sistema no parece poder resolverse.
Sin embargo, los generadores de corriente nos aportan información útil: si bien cada uno
introduce una nueva incógnita en el sistema de ecuaciones de malla, también es cierto que
cada uno introduce una nueva ecuación en el sistema. Al final se obtiene un sistema fácilmente
resoluble (dentro de lo que cabe). La cuestión ahora es, ¿qué ecuación introduce una fuente de
corriente? Supongamos el ejemplo de la Figura 5.36 para explicar el procedimiento de forma
más detallada.
En el ejemplo de la Figura 5.36 se nos pide hallar la corriente que circula por la fuente de
tensión de 10V .
Para resolver el circuito por el método de las mallas, hay que definir inicialmente corrientes
de malla, que como haremos a lo largo de todo este texto, se asignarán siempre a mallas
indivisibles. Además, dado que hay dos generadores de corriente, hay que asignarle, a cada
uno, tanto un valor de tensión (desconocido; será una incógnita) como una polaridad a gusto
del consumidor (polo positivo y negativo). La Figura 5.37 muestra el circuito con las corrientes
de malla apropiadas ası́ como con las fuentes de corriente polarizadas.
Analicemos con detalle la Figura 5.37. Se han asignado corrientes de malla las dos mallas
del circuito (mallas indivisibles), I1 e I2 , ambas con sentido antihorario. Como hay fuentes de
100
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
corriente, a cada una se le debe asignar una polaridad y un valor de tensión. La idea es que cada
fuente de corriente se comporte, a nivel práctico, como una fuente de tensión. A la fuente de
5mA se le ha asignado el polo positivo al extremo de abajo, y el negativo al extremo de arriba.
Recordemos que el modo de llevar a cabo esta asignación no tiene relevancia, y podrı́a haberse
hecho justo al revés. Además, el valor de tensión desconocido que soportan los extremos de
esta fuente se ha denominado V1 . Según la polaridad asignada y el valor de tensión, se cumple
que VD − VC = V1 (diferencia de tensión entre el polo positivo y el negativo es igual al valor
de la fuente). A la fuente de corriente de 10mA se le ha asignado el polo positivo al extremo
de arriba, mientras que el negativo se le ha asignado al extremo de abajo. Nuevamente, la
polaridad podrı́a haber sido la contraria (polo positivo abajo y negativo arriba). El valor de
tensión que hay entre los extremos de esta fuente se ha denominado V2 , de modo que, según la
polaridad asignada a la fuente, se cumple que VA − VB = V2 (diferencia de tensión entre el polo
positivo y el negativo es igual al valor de la fuente).
Hecho esto, se obtienen las ecuaciones de malla, considerando la presencia de las fuentes de
corriente, que a efectos prácticos se comportan como fuentes de tensión:
V1 + V2 = 2000I1
−V2 + 5 = 1000I2
(Malla de I1 )
(Malla de I2 )
Analicemos en detalle estas ecuaciones. La ecuación de la malla de I1 consta de 2 generadores
de corriente, que se comportan como fuentes de tensión a la hora de obtener la ecuación de
malla. Como la corriente I1 atraviesa a ambas fuentes desde su polo negativo a su polo positivo
(recordemos que estas polaridades habı́an sido definidas por nosotros), entonces sus valores de
tensión, V1 y V2 , suman. Por otro lado, aunque una de las ramas sea compartida, por las dos
mallas (la rama de la fuente de corriente de 10mA), al no haber resistencias en ella, no influye
en las ecuaciones.
La ecuación de la malla de I2 consta de dos generadores, uno de tensión y otro de corriente.
El valor del generador de tensión suma, ya que la corriente de malla I2 lo atraviesa desde su polo
negativo a su polo positivo. Por contra, el valor de tensión asignado a la fuente de corriente,
V2 , resta, ya que la corriente de malla I2 lo atraviesa desde su polo positivo a su polo negativo.
Para nuestra desgracia, tenemos un sistema de dos ecuaciones con cuatro incógnitas. Necesitamos dos ecuaciones más para poder resolverlo; las ecuaciones buscadas provienen de las
fuentes de corriente, una ecuación por cada fuente. Pensemos en la fuente de corriente de 5mA.
Según esa fuente de corriente, por la rama A-C-D-B del circuito de la Figura 5.37 circula una
corriente de 5mA, con sentido A-C-D-B. ¿Qué relación puede tener esa corriente con las corrientes de malla? Cuando explicábamos el método de las mallas al principio de esta sección, en
el último paso (paso de resolución), explicamos cómo se relacionan las corrientes de malla con
las corrientes que hay en cada rama del circuito. Según esa relación, la corriente de malla I1 del
circuito coincide exactamente con la corriente que circula por la rama A-D-B, y que coincide a
su vez con la corriente que impone la fuente de corriente de 5mA. La ecuación por tanto que
impone la fuente de corriente de 5mA es:
I1 = 5 · 10−3
Nótese que si la corriente de malla I1 se hubiera supuesto circular en sentido horario, en vez de
antihorario, su valor habrı́a sido de −5mA.
Fijémonos ahora en la fuente de corriente de 10mA. Esa fuente de corriente está situada
en una rama compartida por varias mallas. La corriente que circula por esa rama, según se
explicó anteriormente en el paso de resolución del método de las mallas, se puede obtener
suponiéndole un sentido de circulación aleatorio, y en base a dicho sentido, obtenerse como
combinación de las corrientes de malla que a ella contribuyen. Si suponemos que la corriente
101
5.3. MÉTODO DE LAS MALLAS
que circula por la rama de la fuente de corriente de 10mA circula hacia arriba, y la llamamos
I10mA , entonces se tiene que:
I10mA = I1 − I2
Ya que la corriente I1 llega a la rama con sentido hacia arriba (coincide con el supuesto a la
corriente de la rama, y por tanto suma), y la corriente I2 llega a la rama con sentido hacia
abajo (no coincide con el supuesto a la corriente de la rama, y por tanto resta). Pero es que,
además, sabemos que la fuente de corriente inyecta en esa rama una corriente de 10mA y hacia
arriba, y por tanto la corriente que hemos llamado I10mA vale necesariamente 10mA, es decir:
I1 − I2 = 10 · 10−3
La corriente que circula por la rama de la fuente de 10mA se podrı́a haber supuesto circulando
hacia abajo. En ese caso, el valor de I10mA habrı́a sido de −10mA, y la ecuación asociada,
I2 − I1 = −10 · 10−3 , lo que vendrı́a a haber sido una ecuación equivalente a la anterior (como
siempre, no importa el sentido de circulación que se supone para una corriente).
Tras todo esto, el sistema de ecuaciones que tenemos es el siguiente:
De donde se obtiene, trivialmente:

V1 + V2 = 2000I1



−V + 5 = 1000I
2
2
−3

I1 = 5 · 10



I1 − I2 = 10 · 10−3
I1 = 5mA, I2 = −5mA, V1 = 0V, V2 = 10V
La corriente que circula por la fuente de tensión coincide con la corriente de malla I2 . Por
tanto, la corriente que circula por la fuente de tensión es de valor −5mA, y circula hacia arriba.
Equivalentemente, se puede decir que la corriente que atraviesa la fuente de tensión es de 5mA,
y circula hacia abajo.
5.3.2.
Método de las mallas, ejercicios
En esta sección pasamos a resolver una serie de ejercicios de circuitos de corriente continua
mediante el método de las mallas.
Ejercicio 5.13: Se pide, para el circuito de la Figura 5.38, calcular la tensión Vo (suponer
β = 100).
80KΩ
βI
0,6V
5V
Vo
5KΩ
I
20KΩ
1KΩ
Figura 5.38: Ejemplo 5.13
5V
102
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
I
80KΩ
0,6V
+
βI Vg
-
Vo
A
5KΩ
5V
20KΩ
I1
1KΩ
I2
5V B
I3
Figura 5.39: Ejemplo 5.13, corrientes de malla asignadas
Solución Para resolver un circuito por el método de las mallas, se debe comenzar siempre
definiendo las corrientes de malla en cada una de las mallas de interés. Como además hay una
fuente de corriente (que es dependiente, para más inri), a ésta hay que asignarle tanto una
polaridad como un valor de tensión desconocido, digamos Vg . Recuérdese que los sentidos de
las corrientes de malla son elegidos por nosotros, ası́ como la polaridad asociada a la fuente de
corriente. Nuestra elección se muestra en la Figura 5.39.
Ahora debemos obtener las ecuaciones de malla asociadas a las tres mallas. Recuérdese que,
dado que hay una fuente de corriente, las ecuaciones de malla no serán suficientes para resolver
el circuito, necesitándose una más en este caso, y la cual es proporcionada por la fuente de
corriente dependiente. Las ecuaciones de malla son:
5 = I1 (80000 + 20000) − 20000I2
−0,6 = I2 (20000 + 1000) − 20000I1 − 1000I3
−Vg − 5 = I3 (1000 + 5000) − 1000I2
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
Como hemos dicho, nos queda ver qué información nos aporta la fuente de corriente. ¿Qué ecuación es la que nos da, y que nos permite resolver el sistema?
Si nos fijamos en la fuente de corriente, ésta inyecta una corriente de valor βI, hacia la
izquierda, en la rama donde se sitúa. Ahora bien, la corriente I3 resulta ser la corriente que hay
en esa misma rama (en esa rama no confluyen más corrientes de malla, y por tanto la corriente
que hay es I3 ). El problema que hay es que el sentido de la corriente que inyecta la fuente es
opuesto (hacia la izquierda), que el de la corriente de malla I3 en esa rama (hacia la derecha).
Para solventar este problema, recordamos que una corriente es equivalente a otra de sentido de
circulación opuesto y de valor cambiado de signo. Por tanto, la corriente que inyecta la fuente
es equivalente a otra que circula hacia la derecha y de valor −βI, corriente que coincidirı́a con
I3 , ya que ésta circula hacia la derecha en la rama de la fuente de corriente. Se tiene por tanto
que:
I3 = −βI = −100I
Otro modo de llegar a esa conclusión consiste en sustituir la fuente de corriente por una equivalente, cuyo sentido de circulación es hacia la derecha, y cuyo valor es el opuesto (cambiado de
signo) de la original. En ese caso es evidente que I3 coincide directamente con la corriente de
la fuente, obteniéndose la ecuación anterior.
Además, I2 coincide con la corriente que se ha llamado I, es decir:
I2 = I
103
5.3. MÉTODO DE LAS MALLAS
El sistema de ecuaciones de malla queda en:


5 = 100000I1 − 20000I
−0,6 = 21000I − 20000I1 + 100000I


−Vg − 5 = −600000I − 1000I
De donde se obtiene:
I1 = 5,068 · 10−5 A, I = 3,419 · 10−6 A, Vg = −2,945V
De aquı́ se puede deducir el valor de I3 :
I3 = −100I = −3,419 · 10−4 A
Pero justamente I3 coincide con la corriente que atraviesa la rama de la resistencia de 5KΩ,
con sentido de A a B, y por tanto se puede escribir:
VA − VB
⇔
5000
VA − 5
⇔ VA = 3,290V
−3,419 · 10−4 =
5000
Donde se ha hecho uso de VB = 5, tal y como impone la fuente de tensión de 5V de la derecha.
Por otro lado, justamente VA coincide con Vo , pues ambos puntos están cortocircuitados, es
decir:
Vo = 3,290V
I3 =
Ejercicio 5.14: Para el circuito de la Figura 5.40 se pide calcular las potencias generadas o
consumidas por todas las fuentes.
1KΩ
+
10V −
2KΩ
1KΩ
2KΩ
10mA
Figura 5.40: Ejemplo 5.14
Solución
El primer paso para la resolución del circuito por el método de las mallas es la definición
de las corrientes de malla. Además, dado que el circuito presenta una fuente de corriente, es
necesario definirle una polaridad ası́ como un valor de tensión desconocido, digamos Vg . La
Figura muestra el circuito con las corrientes de malla definidas y con una polaridad y valor de
tensión asignados a la fuente de corriente.
Del circuito de la Figura 5.41 se pueden deducir las siguientes ecuaciones de malla:
10 = I1 (1000 + 1000) − 1000I2
0 = I2 (1000 + 2000 + 2000) − 1000I1 + 2000I3
Vg = 2000I3 + 2000I2
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
104
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
2KΩ
+V
+
10V −
1KΩ
I1
2KΩ
I2
I3
g
10mA
-
Figura 5.41: Ejemplo 5.14, corrientes de malla asignadas
Las ecuaciones de malla, por sı́ solas, no son suficientes para resolver el circuito, debido a la
presencia de la fuente de corriente. Para poder resolverlo necesitamos una ecuación más, que
proviene precisamente de la fuente de corriente.
Si nos fijamos con detalle en la corriente de malla I3 , ésta coincide con la corriente de la
rama donde se encuentra la fuente de corriente. Por otro lado, la fuente de corriente impone
en esa rama una corriente con el mismo sentido de circulación de la corriente de malla I3 , y de
valor 10mA. Se deduce, por tanto, que:
I3 = 10 · 10−3
Si se resuelve el sistema formado por las ecuaciones de malla junto con esta última ecuación,
se obtiene:
−1
40
1
A,I2 =
A,I3 = 10 · 10−3A, Vg = V
I1 =
300
300
3
Para obtener las potencias generadas o consumidas en cada uno de los generadores, es necesario
saber tanto la corriente que atraviesa al generador como la tensión que soporta entre sus
extremos (ecuación (1.3)). La corriente que atraviesa a la fuente de tensión coincide con la
corriente de malla I1 , y la tensión que soporta la fuente de corriente es Vg . Recuérdese que la
ecuación (1.3) obliga a que, si la corriente considerada circula de A a B, entonces la tensión
que se mida sea VAB .
• Fuente de tensión: la corriente que la atraviesa desde el polo negativo al polo positivo es
justamente I1 . La diferencia de tensión que debe usarse es, por tanto, la que hay entre el
polo negativo y el polo positivo. Como según la fuente V+ − V− = 10 ⇒ V−+ = V− − V+ =
−10, y la potencia es:
P1 = I1 V−+ =
1
−1
(−10) =
W ≈ −0,033W
300
30
Al ser potencia negativa, se trata de potencia generada, es decir, potencia que la fuente
libera para poder ser usada por el resto del circuito.
• Fuente de corriente: la corriente que la atraviesa desde el polo negativo que le hemos
asignado al polo positivo que le hemos asignado es justamente la corriente de la fuente,
es decir, 10mA. Por otro lado, la diferencia de tensión que debe usarse es la que se mide
entre el polo negativo y el polo positivo. Según la polaridad asignada y el valor de tensión
asignado (Vg ), tenemos que V+ − V− = Vg ⇒ V−+ = V− − V+ = −Vg = −40/3. La potencia
es, por tanto:
−1
1
(−10) =
W ≈ −0,033W
P2 = I1 V−+ =
300
30
Como se trata de potencia negativa, es potencia que la fuente genera, es decir, potencia
que la fuente libera y que es consumida por otros elementos del circuito.
105
5.3. MÉTODO DE LAS MALLAS
1KΩ
1KΩ
1KΩ
B
1KΩ
10V
30V
10mA
20V
Figura 5.42: Ejemplo 5.15
1KΩ
10V
1KΩ
-
Vg
10mA
+
I1
1KΩ
B
1KΩ
30V
C
20V
I2
I3
Figura 5.43: Ejemplo 5.15, corrientes de malla asignadas
Ejercicio 5.15: Determinar la tensión en el nudo B en el circuito de la Figura 5.42.
Solución
Para resolver el circuito mediante el método de las mallas es necesario definir corrientes
de malla adecuadas. La presencia de una fuente de corriente nos obliga, además, a definirle a
ésta una polaridad ası́ como un valor de tensión desconocido, el cual llamaremos Vg . La Figura
5.43 muestra las corrientes de malla consideradas ası́ como la polaridad asignada a la fuente de
corriente.
Según las corrientes de malla consideradas, se obtienen las siguientes ecuaciones de malla:
10 + Vg = 1000I1
−Vg − 20 = I2 (1000 + 1000) − 1000I3
20 − 30 = I3 (1000 + 1000) − 1000I2
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
Como el circuito presenta una fuente de corriente, las ecuaciones de malla no son suficientes
para poder resolverlo, ası́ que necesitamos la ecuación que impone la fuente de corriente.
Según las ecuaciones de malla definidas, si consideramos que la corriente que circula por la
rama de la fuente de corriente (Ig ) se dirige hacia arriba, entonces su expresión, en función de
las corrientes de malla, es:
Ig = I2 − I1
Por otro lado sabemos que la fuente de corriente impone en la rama en la que se sitúa una
corriente hacia arriba de valor 10mA. Como esa corriente coincide con la que hemos llamado
106
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Ig , se deduce que Ig = 10 · 10−3 . Se tiene por tanto que:
10 · 10−3 = I2 − I1
Usando el sistema de ecuaciones formado por las ecuaciones de malla junto con la ecuación que
impone la fuente de corriente se puede resolver el sistema, y se obtiene:
I1 = −0,012A, I2 = −2 · 10−3 A, I3 = −6 · 10−3 A, Vg = −22V
Debemos hallar la tensión en el nodo B. La fuente de tensión de 20V dicta V+ −V− = 20, y como
el polo negativo está cortocircuitado con la toma de tierra (V− = 0), y el polo positivo coincide
con C (V+ = VC ), se tiene que VC = 20. Para obtener la tensión en el nodo B necesitamos saber
qué corriente circula por la resistencia de 1KΩ que hay entre los puntos B y C. Si suponemos
que dicha corriente circula hacia abajo, su valor, según las corrientes de malla, es:
IBC = I2 − I3 = −2 · 10−3 + 6 · 10−3 = 4 · 10−3
Si ahora usamos la expresión de la corriente IBC según la Ley de Ohm, se obtiene el valor de
VB :
VB − VC
⇔
1000
VB − 20
=
⇔
1000
VB = 24V
IBC =
4 · 10−3
Ejercicio 5.16: Obtener la corriente que circula por la resistencia de 1,5KΩ en el circuito de
la Figura 5.44.
1KΩ
1KΩ
1,5KΩ
10V
1KΩ
10mA
Figura 5.44: Ejemplo 5.16
Solución
Para resolver el circuito por el método de las mallas, se procederá como siempre. En primer
lugar, se definen corrientes de malla. Además, como el circuito consta de una fuente de corriente,
a ésta se le debe asignar una polaridad ası́ como un valor de tensión entre sus terminales, que
llamaremos Vg . La Figura 5.45 muestra el circuito con las corrientes de malla definidas ası́ como
con una polaridad asignada a la fuente de corriente.
Las ecuaciones de malla que se obtienen del circuito de la Figura 5.45 son las siguientes:
10 = I1 (1000 + 1000) + 1000I2
−Vg = I2 (1000 + 1000) + 1000I1
−Vg = 1500I3
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
107
5.3. MÉTODO DE LAS MALLAS
1KΩ
1KΩ
10V
1,5KΩ
1KΩ
Vg
10mA
+
I1
I2
I3
Figura 5.45: Ejemplo 5.16, corrientes de malla definidas
Como en el circuito hay una fuente de corriente, no se puede resolver el sistema de ecuaciones
solamente con las ecuaciones de malla. Es necesario obtener otra ecuación de la fuente de
corriente. Fijémonos en que, si suponemos que la corriente que circula por la rama de la fuente de
corriente (I10mA ) tiene un sentido de circulación hacia arriba, entonces su expresión algebraica
en base a las corrientes de malla es:
I10mA = I1 + I2
Pero es que además la fuente de corriente impone en su rama una corriente que circula hacia
arriba y de valor 10mA, corriente que coincide con la que nosotros hemos llamado I10mA , es
decir, I10mA = 10 · 10−3 , y por tanto:
10 · 10−3 = I1 + I2
Si resolvemos el sistema de ecuaciones formado por las ecuaciones de malla junto con ésta
última ecuación, se obtiene:
I1 =
1
1
1
A, I2 =
A, I3 =
A, Vg = −10V
300
300
150
Se nos pide hallar la corriente que circula por la resistencia de 1,5KΩ. Esa corriente coincide
con la corriente de malla I3 , es decir, la corriente que circula por la resistencia de 1,5KΩ tiene
el sentido de circulación de I3 y su valor es:
I1,5KΩ =
1
A ≈ 6,67 · 10−3 A
150
Ejercicio 5.17: En el circuito de la Figura 5.46 se pide obtener la tensión Vo .
Solución
Antes de comenzar a resolver este circuito, podemos intentar simplificarlo. Fijémonos en que
las dos resistencias verticales de la derecha están conectadas en paralelo, y como tales pueden
asociarse. Cabrı́a preguntarse si en efecto tal asociación nos conviene. Recuérdese (sección
4.4) que cuando se asocian elementos en un circuito, hay información que se pierde, de modo
que hay parámetros del circuito original que no pueden obtenerse directamente en el circuito
simplificado. Por suerte, no es este nuestro caso; en el ejemplo actual, se nos está pidiendo
obtener la tensión Vo . Al asociar en paralelo, los terminales de los elementos asociados se
mantienen inalterados, y siguen existiendo en el circuito original (ver Figura 4.48, puntos C y
D). Por tanto, si asociamos las dos resistencias, los dos extremos, uno de ellos el de Vo , sigue
108
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
1KΩ
Vo
1KΩ
10V
1KΩ
1KΩ
10mA
Figura 5.46: Ejemplo 5.17
1KΩ
1KΩ
Vo
1KΩ
10V
500KΩ
10mA
Figura 5.47: Ejemplo 5.17, resistencias asociadas en paralelo
existiendo en el circuito simplificado, y por tanto la tensión Vo puede calcularse en el circuito
de la Figura 5.47, que muestra las dos resistencias asociadas en paralelo.
Simplificado el circuito (simplificación que nos ha permitido eliminar una malla del circuito),
aplicamos el método de las mallas para su resolución. En primer lugar, definimos corrientes de
malla apropiadas. Como además el circuito tiene una fuente de corriente, a ésta se le debe
asociar tanto una polaridad como un valor de tensión, el cual designaremos como Vg . La Figura
5.48 muestra el circuito con las corrientes de malla supuestas ası́ como con la polaridad asociada
a la fuente de corriente.
Del circuito de la Figura 5.48 se obtienen las siguientes ecuaciones de malla:
Vg − 10 = I1 (1000 + 1000) + 1000I2
Vg = I2 (1000 + 1000 + 500) + 1000I1
(Malla de I1 )
(Malla de I2 )
Es necesario, además, obtener una ecuación de la fuente de corriente para poder resolver el
sistema. Si suponemos que la corriente que circula por la rama de la fuente de corriente (I10mA )
1KΩ
1KΩ
Vo
1KΩ
10V
+
I1
-
Vg
10mA
500KΩ
I2
B
Figura 5.48: Ejemplo 5.17, corrientes de malla asignadas
109
5.3. MÉTODO DE LAS MALLAS
circula hacia arriba, entonces su expresión algebraica en función de las corrientes de malla es:
I10mA = I1 + I2
Además, justamente la corriente que impone la fuente de corriente en su rama es una corriente
que circula hacia arriba, y de valor 10mA. Esta corriente coincide con la que nosotros hemos
llamado I10mA , es decir, I10mA = 10 · 10−3 , teniéndose:
10 · 10−3 = I1 + I2
Resolviendo el sistema formado por las ecuaciones de malla y la ecuación de la fuente de
corriente, se obtiene:
I1 = 2 · 10−3 A, I2 = 8 · 10−3A, Vg = 22V
Ahora bien, usando un poco la cabeza, nos podemos dar cuenta de que la corriente I2 coincide
con la que atraviesa a la resistencia de 500Ω, y por tanto puede escribirse, según la Ley de
Ohm, como:
Vo − VB
I2 =
500
Usando el valor de I2 hallado y teniendo en cuenta que VB = 0 dado que B está cortocircuitado
con la toma de tierra, se obtiene:
Vo − 0
⇔
500
Vo = 4V
8 · 10−3 =
Ejercicio 5.18: Se pide determinar la corriente que circula por la resistencia R del circuito
de la Figura 5.49.
1KΩ
10V
2KΩ
R=1KΩ
1KΩ
20V
1KΩ
Figura 5.49: Ejemplo 5.18
Solución
Vamos a pensar un poco antes de comenzar a resolver este circuito por el método de las
mallas. Para algo tenemos cerebro y culo, ambos órganos con los que piensan la mayorı́a de las
personas. El circuito actual podrı́a resolverse suponiendo tres corrientes de malla, planteando
el sistema de ecuaciones, y resolviéndolo. Si llamásemos I3 a la corriente de malla de la malla
de la derecha, ésa serı́a la corriente buscada, la que circula por la resistencia R. Sin embargo,
se tratarı́a de un sistema de tres ecuaciones con tres incógnitas, y dado que somos perrı́simos
en extremo, intentaremos reducirlo en la medida de lo posible.
110
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
10V
2KΩ
R=1KΩ
A
1KΩ
1KΩ
20V
B
Figura 5.50: Ejemplo 5.18, ¿se pueden asociar las dos resistencias entre A y B?
Fijémonos en la Figura 5.50. No hay que ser un genio para darse cuenta de que la resistencia
llamada R ası́ como la otra resistencia de 1KΩ situada entre los puntos marcados como A y
B están conectadas en paralelo. Si asociáramos ambas resistencias en paralelo, sin embargo, se
perderı́a la rama de la resistencia R (tal y como se explicaba en la sección 4.4), y por tanto
en el circuito simplificado no serı́a posible obtener de forma directa el valor de la corriente que
circulaba por la resistencia R en el circuito original. Ahora bien, al asociarse ambas resistencias,
los puntos A y B, extremos de las dos resistencias asociadas, siguen existiendo en el circuito
simplificado. Por tanto, en dicho circuito se podrı́a obtener el valor de la diferencia de tensión
VAB = VA − VB , ya que dichos puntos, insistimos, siguen existiendo en el circuito simplificado.
Obtenido el valor de VAB es trivial obtener el valor de la corriente que circula por la resistencia
R en el circuito original, ya que dicha corriente, supuesta circulando hacia la derecha a través
de la resistencia R, tomarı́a el siguiente valor según la Ley de Ohm:
IAB =
VA − VB
VAB
=
R
R
El procedimiento que seguiremos será, pues, el siguiente:
• Asociar las dos resistencias de 1KΩ cuyos terminales son los puntos A y B.
• En el circuito obtenido, obtener el valor de la diferencia de tensión VAB .
• Mediante dicho valor de tensión, obtener el valor de la corriente que circula por la resistencia R del circuito original, mediante la expresión IR = VAB /R.
Además, para obtener la diferencia de tensión VAB , colocaremos una toma de tierra cortocircuitada con el punto B. Recuérdese que colocar una toma de tierra en un circuito no varı́a
las diferencias de tensión existentes entre cualesquiera dos puntos de un circuito (sección 1.2).
Es decir, aun colocando la toma de tierra en B, la diferencia de tensión VAB del circuito con la
toma de tierra será la misma. La ventaja en nuestro caso es que, al colocar la toma de tierra
en B, se tendrá que VB = 0, y por tanto VAB = VA − VB = VA , es decir, la diferencia de tensión
buscada coincidirá con la tensión en el punto A.
La Figura 5.51 muestra el circuito con las dos resistencias asociadas en paralelo, ası́ como
con las corrientes de malla asignadas a cada una de las mallas del circuito. Obsérvese que no
hay fuentes de corriente (al fin, ¡un circuito sin fuentes de corriente!), y por tanto se puede
resolver por mallas sin necesidad de obtener ecuaciones extras.
Las ecuaciones de malla que se obtienen del circuito son las siguientes:
10 − 20 = I1 (1000 + 1000) − 1000I2
20 = I2 (1000 + 2000 + 500) − 1000I1
(Malla de I1 )
(Malla de I2 )
111
5.3. MÉTODO DE LAS MALLAS
1KΩ
2KΩ
10V
A
1KΩ
500KΩ
20V
I1
I2
Figura 5.51: Ejemplo 5.18, corrientes de malla definidas
De donde se obtiene:
I1 = −2,5 · 10−3 A, I2 = 5 · 10−3 A
Justamente I2 coincide con la corriente que atraviesa la resistencia de 500Ω, de arriba a abajo,
y por tanto, según la Ley de Ohm, su expresión es:
I2 =
VA
500
De donde:
VA
⇔
500
VA = 2,5V
5 · 10−3 =
Este valor de tensión coincide, tal y como hemos explicado, con la diferencia de tensión VAB
del circuito original, y por tanto, la corriente IR que atraviesa la resistencia R, con sentido de
A a B, es:
VAB
2,5
IR =
=
= 2,5 · 10−3 A
R
1000
Ejercicio 5.19: Determinar la tensión Vo en el circuito de la Figura 5.52.
1KΩ
1KΩ
1KΩ
1KΩ
1KΩ
Vo
10V
10mA
1KΩ
10mA
Figura 5.52: Ejemplo 5.19
Solución
Para resolver el circuito, haremos uso del método de las mallas. Definimos tres corrientes
de malla, I1 , I2 e I3 . Además, como hay dos generadores de corriente, a cada uno se le debe
112
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
1KΩ
1KΩ
1KΩ
A
Vo
I
+
Vg1
1KΩ
10mA
+
I1
-
10V
Vg2
10mA
I2
1KΩ
I3
Figura 5.53: Ejemplo 5.19, corrientes de malla asignadas
asignar tanto una polaridad como un valor de tensión desconocido (Vg1 para el generador de
la izquierda y Vg2 para el generador de la derecha). La Figura 5.53 muestra el circuito con las
corrientes de malla asignadas y las fuentes de corriente con polaridad asignada.
Es importante fijarse en un detalle. La resistencia situada en el extremo derecho del circuito,
la de Vo , es una resistencia por la que no circula corriente alguna. Fijémonos en que la resistencia
acaba en un circuito abierto, y por tanto por ella no puede circular corriente (¿a dónde irı́a la
corriente que por ella circulase? ¿Saltarı́a al vacı́o?). Se deduce por tanto que la corriente que
se ha denominado I en el circuito de la Figura 5.53, es nula, y por tanto:
VA − Vo
=0⇔
I=
1000
VA = Vo
Es decir, la tensión Vo buscada es igual a la tensión que hay en el punto A, detalle que se
tendrá en cuenta a la hora de resolver el circuito.
Las ecuaciones de malla que se obtienen son las siguientes:
Vg1 − Vg2 = I1 (1000 + 1000) − 1000I2
Vg2 − 10 = I2 (1000 + 1000) − 1000I1
10 = I3 (1000 + 1000)
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
Del generador de corriente de la izquierda se deduce que:
I1 = 10 · 10−3
ya que la corriente que éste inyecta coincide con la corriente de malla I1 .
Referente al generador de corriente de la derecha. Supongamos que la corriente que circula
por la rama de dicho generador (Ig ), circula hacia arriba. Entonces, su expresión según las
corrientes de malla es:
Ig = I2 − I1
Pero justamente Ig es la corriente que el generador de corriente inyecta en su rama, es decir,
Ig = 10 · 10−3 , y se tiene:
10 · 10−3 = I2 − I1
Resolviendo el sistema de las tres ecuaciones de malla ası́ como de las dos ecuaciones de los
generadores de corriente,


Vg1 − Vg2 = I1 (1000 + 1000) − 1000I2





Vg2 − 10 = I2 (1000 + 1000) − 1000I1
10 = I3 (1000 + 1000)



I1 = 10 · 10−3



10 · 10−3 = I − I
2
1
113
5.3. MÉTODO DE LAS MALLAS
se obtiene:
I1 = 10 · 10−3 A, I2 = 20 · 10−3 A, I3 = 5 · 10−3 A, Vg1 = 40V, Vg2 = 40V
Además, según la Ley de Ohm, I3 , corriente que circula por la rama vertical cuyo extremo
superior está conectado al punto A, es:
I3 =
VA
1000
de donde:
VA
⇔
1000
VA = Vo = 5V
5 · 10−3 =
Nótese cómo, para resolver el circuito, no era necesario resolver todo el sistema de ecuaciones.
De la ecuación de malla deI3 ya se podı́a obtener el valor de I3 , a partir del cual obtener VA . Si
bien en este texto queremos llegar al máximo nivel de detalle en la resolución de los circuitos,
echemos un poco de cabeza: normalmente no se perderı́a el tiempo resolviendo todo el sistema.
Ejercicio 5.20: Se pide determinar la potencia consumida por la resistencia R del circuito de
la Figura 5.54.
1KΩ
5V
6KΩ
6KΩ
1KΩ
10V
20V
R=2KΩ
Figura 5.54: Ejemplo 5.20
Solución
Resolver este circuito es bastante sencillo mediante mallas. Simplemente basta definir las
corrientes de malla adecuadas, y resolver el sistema de ecuaciones de malla obtenido. Al no haber
fuentes de corriente, el sistema se puede resolver sin necesidad de aportar más ecuaciones.
La Figura 5.55 muestra el circuito con las corrientes de malla definidas para cada malla
indivisible.
En base a esas corrientes de malla, las ecuaciones de malla que se obtienen son:
−10 = I1 (6000 + 6000) − 6000I2
10 − 5 − 20 = I2 (6000 + 1000) − 6000I1 − 1000I3
20 = I3 (1000 + 1000 + 2000) − 1000I2
De donde se obtiene:
I1 =
−17
A, I2 = −4 · 10−3 A, I3 = 4 · 10−3 A
6000
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
114
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
5V
6KΩ
I1
6KΩ
1KΩ
10V
20V
I2
R=2KΩ
I3
Figura 5.55: Ejemplo 5.20, corrientes de malla definidas
Para obtener la potencia consumida por la resistencia R, podemos hacer uso de la ecuación
(2.2), que nos dice que la potencia consumida por una resistencia es igual al producto de la
corriente que la atraviesa, al cuadrado, y el valor de la resistencia. Como la corriente I3 coincide
con la corriente que atraviesa la resistencia R, dicha potencia será:
PR = I3 2 R = (4 · 10−3 )2 · 2000 = 0,032W
Ejercicio 5.21: Se pide determinar la resistencia equivalente, medida entre los terminales A
y B, del sistema de la Figura 5.56.
A
1KΩ
1KΩ
B
1KΩ
1KΩ
2KΩ
Figura 5.56: Ejemplo 5.21
Solución
El presente se trata de un ejercicio de asociaciones, más que de aplicar el método de las
mallas. Digo de asociaciones, porque el circuito puede resolverse mediante cutre asociaciones
serie y paralelo. Cuando en su dı́a planteé este ejercicio por primera vez, creı́a que la resistencia
equivalente de este circuito sólo podı́a obtenerse mediante el método genérico (sección 4.1).
Cinco segundos de un no intenso análisis del circuito, lleva a cualquier ser con algo más de
inteligencia que la de un Plátano de Canarias, a la conclusión de que la resistencia equivalente
se puede obtener mediante simples asociaciones en serie y paralelo. El único consuelo que me
queda, es saber que ahora soy intelectualmente tan capaz como un Plátano de Canarias.
Ası́ pues, resolveremos el circuito mediante simples asociaciones. Se deja al lector, como ejercicio, comprobar que mediante el método genérico se obtiene el mismo valor para la resistencia
equivalente. Eso sı́, que el lector vaya a aceptar esta sugerencia, es algo que no me creo ni yo, ni
el lector, ni nadie en su sano juicio... ¿alguien ha seguido alguna vez este tipo de sugerencias?
La Figura 5.57 muestra las dos primeras resistencias que van a ser asociadas, rodeadas por
un globo. Las dos resistencias marcadas están conectadas en serie, ya que ambas están situadas
en la misma rama del circuito, la rama D-F-E.
115
5.3. MÉTODO DE LAS MALLAS
A
1KΩ
C
1KΩ
D
1KΩ
1KΩ
2KΩ
B
E
F
Figura 5.57: Ejemplo 5.21, las primeras resistencias que asociar
A
1KΩ
C
1KΩ
D
1KΩ
3KΩ
B
E
Figura 5.58: Ejemplo 5.21, siguientes resistencias que asociar
Dado que esas resistencias se van a asociar en serie, el valor de la resistencia equivalente es
igual a la suma de los valores de cada una de las resistencias, es decir:
Req1 = 2000 + 1000 = 3000Ω
La Figura 5.58 muestra tanto la resistencia asociada Req1 , de 3000Ω, como las dos nuevas
resistencias que van a asociarse (las rodeadas por un globo). Obsérvese cómo, tras la asociación
de las dos resistencias en serie, el punto F del circuito original desaparece, pero los puntos D y
E se mantienen. Las resistencias que se van a asociar en el siguiente paso están conectadas en
paralelo, ya que sus terminales son comunes (puntos D y E). El valor de esta nueva resistencia
equivalente es:
1000 · 3000
Req2 =
= 750Ω
1000 + 3000
La Figura 5.59 muestra tanto la resistencia asociada Req2 , la de 750Ω, como las dos nuevas
resistencias que van a ser asociadas (las rodeadas por un globo). Obsérvese cómo, tras la
asociación de las dos resistencias anteriores, los puntos D y E, extremos de las resistencias
asociadas en paralelo, siguen existiendo. Las dos resistencias que ahora van a asociarse están
conectadas en serie, ası́ que el valor de la resistencia equivalente a ellas dos es:
Req3 = 1000 + 750 = 1750Ω
La Figura 5.60 muestra tanto la resistencia asociada, la de, como las dos nuevas, y últimas,
resistencias que van a ser asociadas (las rodeadas en un globo). Nótese cómo, tras asociar las
dos resistencias en serie, el punto intermedio a ellas, D, ha desaparecido. Las nuevas resistencias
a asociar están conectadas en paralelo, ya que sus terminales son comunes (puntos C y E), y
como tales serán asociadas. El valor de la resistencia equivalente a ellas es:
Req4 =
7000
1000 · 1750
=
Ω
1000 + 1750
11
Ahora bien, tras llevar a cabo esta asociación, tenemos la resistencia equivalente medida entre
los terminales A y B del circuito, es decir:
Req = Req4 =
7000
Ω ≈ 636,36Ω
11
116
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
1KΩ
C
A
D
1KΩ
750Ω
B
E
Figura 5.59: Ejemplo 5.21, siguientes resistencias que asociar
C
A
1750Ω
1KΩ
B
E
Figura 5.60: Ejemplo 5.21, últimas resistencias que asociar
Es importante fijarse, en este sentido, cómo a lo largo de todo el proceso de asociaciones se ha
procurado mantener los puntos A y B existiendo. Dado que se nos pedı́a la resistencia equivalente entre dichos terminales, no se podı́a llevar a cabo ninguna asociación que los eliminase.
La Figura 5.61 muestra la resistencia equivalente buscada.
Ejercicio 5.22: Obtener el valor de la tensión Vo en el circuito de la Figura 5.62.
Solución
El actual se trata de un circuito con dos mallas indivisibles, a las que asociaremos corrientes
de malla para su resolución por el método de las mallas. Al no haber fuentes de corriente,
estas ecuaciones serán las necesarias para poder resolver el circuito. La Figura 5.63 muestra el
circuito con las corrientes de malla asignadas a cada malla.
Las ecuaciones de malla que se obtienen del circuito de la Figura 5.63 son:
25 = I1 (5000 + 20000) − 5000I2
0 = I2 (5000 + 8000 + 12000) − 5000I1
A
Req=7000/11Ω
B
Figura 5.61: Ejemplo 5.21, resistencia equivalente buscada
(Malla de I1 )
(Malla de I2 )
117
5.3. MÉTODO DE LAS MALLAS
12KΩ
5KΩ
8KΩ
+
25V −
Vo
20KΩ
Figura 5.62: Ejemplo 5.22
12KΩ
A
I2
5KΩ
+
25V −
8KΩ
Vo
20KΩ
I1
Figura 5.63: Ejemplo 5.22, corrientes de malla asignadas
De donde se obtiene:
1
1
A, I2 =
A
960
4800
Fijémonos que I2 coincide con la corriente que atraviesa la resistencia de 12KΩ, y por tanto,
según la Ley de Ohm, puede ser escrita como:
I1 =
I2 =
VA − Vo
12000
El valor de VA se puede obtener directamente de la fuente de tensión: según la fuente de tensión,
la diferencia de tensión entre su polo positivo (A) y su polo negativo (toma de tierra), es igual
a 25V , y por tanto la tensión en A ha de ser de 25V necesariamente. De ahı́ se deduce que:
VA − Vo
⇔
12000
1
25 − Vo
=
⇔
4800
12000
Vo = 22,5V
I2 =
118
CAPÍTULO 5. RESOLUCIÓN DE CIRCUITOS EN DC
Capı́tulo 6
Terminologı́a, simbologı́a y
divisor de tensión
En este capı́tulo se van a tratar tres aspectos de la teorı́a de circuitos que no han tenido
cabida en ningún otro tema de este libro. Se trata de tres apartados sencillos sin ningún tipo de
complejidad, y sin embargo, conceptos muy empleados en el análisis de todo tipo de circuitos.
6.1.
Terminologı́a
En muchas ocasiones se puede oı́r que un circuito es un sistema que, ante una entrada determinada, proporciona una salida determinada. En este sentido, un circuito, ya sea de corriente
continua o no, puede entenderse como una función matemática de variable real, que ante una
entrada determinada proporciona una salida determinada.
Es necesario pues preguntarse cuál es la entrada de un circuito, ası́ como cuál es su salida.
Para entender los conceptos de entrada y de salida de un circuito es preferible basarse en un
ejemplo.
Supongamos el circuito de la Figura 6.1. En tal circuito se nos podrı́a preguntar cuál es el
valor de la corriente Io si el valor de la fuente de tensión Vi es de 5V . Si pensamos detenidamente
nos daremos cuenta de que el valor de la corriente Io depende de forma directa del valor de la
tensión Vi , de tal modo que para cada valor de Vi , tenemos un distinto valor de corriente Io
(Io = Vi /R). En este sentido podemos decir que la corriente Io es la salida del sistema, y Vi la
entrada, ya que el valor de Vi determina el valor de Io . En teorı́a de circuitos lo más común es
que la entrada del circuito sea una tensión o corriente (fuente de tensión o fuente de corriente),
y que la salida sea una tensión o corriente, en un punto o rama del circuito respectivamente.
Qué es considerado entrada o salida de un circuito no depende del circuito en sı́, sino más
bien de uno mismo y del significado que se le quiera dar al circuito. Podemos considerar que la
Vo
Vi
Io
R
Figura 6.1: circuito con entradas y salidas
119
120
CAPÍTULO 6. TERMINOLOGÍA, SIMBOLOGÍA Y DIVISOR DE TENSIÓN
Vi
Io
R
Figura 6.2: ¿cuál es la salida del circuito ante una entrada de 5,6V ?
entrada de un circuito es una fuente determinada (ya sea de tensión o de corriente) elegida por
nosotros, y que la salida es cierta tensión o corriente del circuito, también elegida por nosotros;
la idea es que la entrada y salida elegidas tengan algún sentido y sean útiles a la hora de
analizar el circuito tanto cualitativa como cuantitativamente. En general, si en un enunciado de
un problema se nos pide algo parecido a hallar el valor X de tensión o corriente del circuito si
la fuente Y (de tensión o corriente) tiene un valor determinado, entonces la entrada del circuito
es la fuente Y, y la salida, la tensión o corriente X.
Insistimos, sin embargo, en que el qué es considerado entrada o salida en un circuito depende
exclusivamente de qué decidimos nosotros que queremos que sea entrada o salida. Ası́ por
ejemplo, en el mismo circuito de la Figura 6.1, podrı́amos haber supuesto que la salida del
circuito, en vez de ser la corriente Io , fuese la tensión Vo . En ese caso, la salida entrada del
circuito serı́a Vi y la salida Vo . Obsérvese cómo, formalmente, en este caso también puede
considerarse que el circuito es un sistema que ante una entrada determinada (valor de Vi ), nos
da un valor de salida determinado (Vo ); esto se debe a que el valor de la tensión Vo depende del
valor de tensión Vi de la fuente de tensión(Vo = Vi ).
Existe una notación especial, que ya ha sido usada en algunos ejemplos de este libro, que
nos señala qué es entrada y qué es salida en un circuito. Aquel elemento de un circuito que es
considerado entrada, tiene un valor cuyo nombre acaba en un subı́ndice i 1 . Ası́ por ejemplo,
una fuente de tensión de valor Vi es una fuente de tensión considerada la entrada del circuito,
debido al subı́ndice i. A su vez, todo aquel valor cuyo nombre consta de un subı́ndice o2 es
considerado salida del circuito. Por ejemplo, una tensión del circuito nombrada como Vo serı́a
considerada la salida del circuito.
Con este tipo de terminologı́a, el enunciado de un ejercicio podrı́a ser, por ejemplo: obtener
la salida del circuito de la Figura 6.2 ante una entrada de 5,6V .
En el circuito de la Figura 6.2, la entrada ha de ser la fuente de tensión de valor señalado
como Vi (nótese el subı́ndice i), y la salida, el valor de corriente marcado como Io (nótese el
subı́ndice o). En el enunciado, por tanto, se nos estarı́a pidiendo obtener el valor de la corriente
Io si el valor de la fuente de tensión es Vi = 5,6V , que viene a ser Io = 5,6/R, medida en
amperios.
Al igual que se ha hablado de la entrada de un circuito, es lı́cito hablar de las entradas
de un circuito. En un circuito en el que hay presentes más de una fuente (ya sean de tensión,
de corriente, o de ambos tipos), se puede decir que cada una de esas fuentes constituyen una
entrada para el circuito, y el conjunto de todas ellas, todas las entradas. Cuando estudiemos el
principio de superposición, esta forma de entender las entradas de un circuito será necesaria,
ya que dicho principio se aplica cuando varias fuentes actúan sobre un mismo circuito.
1
2
Del inglés input (entrada).
Del inglés output (salida).
121
6.2. SIMBOLOGÍA
A
R1
V
R2
Figura 6.3: un circuito cualquiera
V
R1
R2
Figura 6.4: circuito equivalente al de la Figura 6.3
6.2.
Simbologı́a
Hasta ahora hemos dibujado todos los circuitos de un modo completo. Cada resistencia
dibujada, representa una resistencia real; cada fuente de tensión, una fuente de tensión real; los
elementos, a su vez, estaban todos conectados por lineas rectas (cortocircuitos), representando
cables de toda la vida de Dios, etc..
Hay, sin embargo, un modo simplificado de representar un circuito determinado. Este método
no nos va a librar de dibujar resistencias o fuentes, pero sı́ de dibujar muchas lineas del circuito.
Supongamos el circuito de la Figura 6.3. En este circuito, está claro que en el punto A,
extremo superior de la resistencia R1 , hay exactamente V voltios.
Pues bien, el circuito de la Figura 6.3 puede redibujarse, de forma equivalente, como el
circuito de la Figura 6.4.
En este nuevo circuito parece haber desaparecido la única malla que hubiera. Es más, este
nuevo circuito parece ser un sinsentido, ya que aparenta ser, sin más, una rama, en circuito
abierto, y por la que, en principio, no parece que podrı́a circular corriente. Eso es lo que
podrı́amos pensar en principio; la verdad es bien distinta: el circuito de la Figura 6.4 es, como
se ha dicho, equivalente al circuito de la Figura 6.3. Ası́ pues, al ver un circuito con el aspecto
del del la Figura 6.4, deberı́amos ser conscientes de que lo que se está representando es un
circuito en el que, dada la toma de tierra situada en el extremo inferior de la resistencia R2 , en
el extremo superior de la resistencia R1 hay una tensión de V voltios (lo cual está se representa
con el circulito hueco y de valor V ); ¿cómo se puede conseguir un circuito como el de la Figura
6.4, en el que en el extremo superior haya V voltios, y en extremo inferior esté la toma de
tierra? En efecto, si colocamos una fuente de tensión de valor V entre extremo superior de la
resistencia R1 y la toma de tierra, se tiene un circuito equivalente. El método general para
obtener el circuito original de un modelo simplificado, es colocar una fuente de tensión de tal
modo que en el punto marcado con el circulito hueco haya tantos voltios como se especifique.
A la hora de resolver el circuito, evidentemente, es preferible tener en mente que el circuito
122
CAPÍTULO 6. TERMINOLOGÍA, SIMBOLOGÍA Y DIVISOR DE TENSIÓN
15V
A
RC
R1
βIB
RB
IB
0,7V
R2
RE
Figura 6.5: un circuito del que, llegado el momento, estaremos hasta los huevecillos
A
RC
R1
15V
βIB
RB
IB
R2
0,7V
RE
Figura 6.6: circuito equivalente al de la Figura 6.5
que realmente se está resolviendo es el no simplificado, en este caso, el de la Figura 6.3.
Supongamos un ejemplo más complejo, como el circuito mostrado en la Figura 6.5.
Obviemos el conjunto moderadamente complejo de resistencias y de fuentes de corriente y
de tensión que hay en el circuito. El circuito de la Figura 6.5 es ciertamente más complejo que
el de la Figura 6.4. Para obtener su modelo normal, y equivalente, basta que dibujemos una
fuente de tensión que haga que, en el punto marcado como A, haya 15V (que es justamente
lo que representa el circuito de la Figura 6.5). Esto se puede conseguir dibujando una fuente
de tensión de valor 15V , cuyo polo positivo esté cortocircuitado con A, y cuyo polo negativo
esté cortocircuitado con la toma de tierra. Es importante notar además que, en un circuito
dibujado de esta forma simplificada, todas las tomas de tierra dibujadas se consideran
un punto común del circuito, es decir, todas las tomas de tierra están cortocircuitadas
entre sı́ (lo cual se debe tener en cuenta a la hora de dibujar el modelo equivalente). Realmente
en un circuito sólo existe una única toma de tierra, y de ahı́ que, aunque se dibujen repetidas
veces, éstas sean consideradas el mismo punto del circuito. La Figura 6.6 muestra el circuito
equivalente.
Tal y como se ha explicado, el modelo equivalente no simplificado se construye colocando
una fuente de tensión de tal modo que en el punto A siga habiendo 15V (que eran los voltios
habidos en el circuito simplificado), lo cual se consigue mediante una fuente de tensión de 15V
cuyo polo positivo está cortocircuitado con el punto A, y cuyo polo negativo está cortocircuitado
123
6.2. SIMBOLOGÍA
R1
Vi
Vo
R2
R3
R4
Figura 6.7: ¿cuál es el circuito real correspondiente?
Vi
A
R1
Vo
R2
R3
R4
Figura 6.8: el circuito de la Figura 6.7, tomas de tierra unidas
con la toma de tierra, justamente como muestra la Figura 6.6. Nótese en el detalle de cómo
todas las tomas de tierra del modelo simplificado se han conectado, dando lugar a una única
toma de tierra común. Al igual que antes, si se pretendiera resolver este circuito, se optarı́a por
emplear el modelo no simplificado, es decir, el de la Figura 6.6.
Veamos otro ejemplo. El circuito de la Figura 6.7 consta de una entrada Vi , y una salida,
Vo .
Nótese como en el circuito se han señalado varias tomas de tierra. Tal y como se ha explicado
con anterioridad, las tomas de tierra pueden unirse para formar una tierra común, tal y como
se muestra en la Figura 6.8.
El siguiente paso es sustituir la entrada Vi por lo que serı́a su representación tı́pica: una
fuente de tensión que impone en el punto A Vi voltios; esto se consigue mediante una fuente
de tensión de valor Vi cuyo polo positivo está conectado al punto A, y cuyo polo negativo
está conectado a la toma de tierra. La Figura 6.9 muestra el circuito equivalente final.
Se preguntará el lector para qué se introduce este tipo de notación simplificada, si en última
instancia hay que plantear el circuito real representado y resolverlo como tal. Visto desde esa
perspectiva, esta nueva notación introducida es más inútil que el papel higiénico mojado. Sin
embargo, cuando se trabaja mucho con esta notación, uno acaba acostumbrándose a resolver
los circuitos sin necesidad de dibujar el circuito real equivalente, con el consiguiente ahorro
en escritura. Se trata simplemente de un modo de intentar simplificar nuestra vida, y que con
un poco de práctica se acaba volviendo como esas tostadas de mantequilla de la cafeterı́a de
la ETSIIT: indispensable. Bromas a parte, esta notación es ampliamente usada en toda la
literatura de teorı́a de circuitos, y como tal se recomienda encarecidamente su aprendizaje.
A
Vi +
−
R1
Vo
R2
R3
R4
Figura 6.9: circuito real equivalente al de la Figura 6.7
124
CAPÍTULO 6. TERMINOLOGÍA, SIMBOLOGÍA Y DIVISOR DE TENSIÓN
R1
R2
C
V2
+
−
+
V1 −
R1
V1
R2
-V2
R3
A
+
V3 −
R3
V3
A
R4
R4
B
B
Figura 6.10: un par de circuitos equivalentes
Vi
R1
+
Vi −
Vo
R2
R1
Vo
R2
Figura 6.11: el clásico divisor de tensión
El último ejemplo de equivalencia entre modelos simplificados y no simplificados es el mostrado en la Figura 6.10.
Es de especial importancia notar cómo, en el circuito de la izquierda, la fuente de tensión
de valor voltios impone en el punto C −V2 voltios. Esto se debe a que la polaridad de la fuente
es tal que el polo positivo está conectado con tierra y el negativo con el punto C (V+ − V− =
V2 ⇔ 0 − VC = V2 ).
Por tanto, a la hora de obtener el modelo simplificado, se debe tener en cuenta que en el
punto C debe haber −V2 voltios, y de ahı́ que el valor que aparece en el circuito de la derecha
es −V2 . Notar también que los dos puntos A y B no representan realmente fuentes de tensión
de ningún tipo, sino puntos de interés del circuito de los cuales, posiblemente, se nos pedirı́a
algún valor (tensión, por ejemplo).
6.3.
Divisor de tensión
Un divisor de tensión es como Dios: está en todas partes.
No le faltaba nada de razón a la persona que, hace ya cinco años, me dijo esas palabras.
Un divisor de tensión es un tipo de circuito que aparece en gran cantidad de ocasiones. Su
estructura es tan sencilla y común dentro de los circuitos que generalmente se resuelven, que
bien merece la pena estudiarlo detenidamente.
La Figura 6.11 represente el clásico divisor de tensión. En esa figura se ha representado al
divisor de tensión de dos formas equivalentes, según la notación simplificada introducida en la
sección 6.2 anterior.
125
6.3. DIVISOR DE TENSIÓN
Vi
R1
+
Vi −
I
R1
Vo
I
R2
Vo
R2
Figura 6.12: aplicando el método de las mallas al divisor de tensión
El divisor de tensión es un circuito que consta de una tensión de entrada Vi , dos resistencias
R1 y R2 conectadas en serie a la fuente, y una salida Vo , tensión existente entre las dos resistencias, considerando que la toma de tierra está conectada a R2 como se muestra en la figura. Nos
preguntamos cuál es el valor de la tensión de salida Vo .
El circuito se pude resolver aplicando el método de las mallas a la única malla existente en
el circuito, como se muestra en la Figura 6.12.
La ecuación de malla que se obtiene es:
Vi = I(R1 + R2 ) ⇔
Vi
I=
R1 + R2
Además, según la Ley de Ohm:
I=
Vo
R2
(6.1)
(6.2)
Si igualamos ambas expresiones de I, (6.1) y (6.2), se tiene:
Vo
Vi
=
⇔
R1 + R2
R2
R2
Vo = Vi ·
R1 + R2
(6.3)
La ecuación (6.3) es la ecuación que describe el comportamiento de un divisor de tensión. Como
el lector comprenderá, esa ecuación no es ningún logro. Es más, a diferencia de otras ecuaciones
importantes, ésta no es fundamental. Sin embargo, insistimos en que un divisor de tensión es
un circuito que aparece en una gran cantidad de ocasiones, y por tanto, el conocer esta fórmula
puede ahorrarnos algo de tiempo en el análisis de circuitos.
Existen versiones más avanzadas de un divisor de tensión, que no estudiaremos. A lo largo
de mi experiencia en teorı́a de circuitos, éste es el que sin duda aparece en mayor cantidad de
ocasiones; de ahı́ que vayamos a obviar los otros tipos de divisores de tensión.
126
CAPÍTULO 6. TERMINOLOGÍA, SIMBOLOGÍA Y DIVISOR DE TENSIÓN
Capı́tulo 7
Teoremas
Con este tema se concluirá este libro dedicado al análisis de circuitos en condiciones de
corriente continua.
En las siguientes páginas se van a introducir tres herramientas muy útiles a la hora de
resolver un circuito. Las asociaciones de elementos suelen simplificar el análisis de un circuito,
si bien hasta ahora hemos hecho un escaso uso de ellas. En este tema se explicarán tres procedimientos que servirán, al igual que las asociaciones de elementos, como herramientas de
simplificación del análisis de circuitos: principio de superposición, teorema de Thevènin y teorema de Norton.
7.1.
Principio de superposición
El principio de superposición se encuentra presente en muchos ámbitos de la fı́sica. Si bien
éste puede aplicar a un sin fin de situaciones, su enunciado viene a ser el mismo: que un sistema
lineal puede ser descompuesto en subsistemas más pequeños, de modo que el comportamiento
o salida del sistema original puede ser obtenido como suma de los comportamientos o salidas
de cada uno de los sistemas reducidos.
El principio de superposición está ı́ntimamente relacionado con el concepto matemático de
linealidad.
Un operador lineal es una función matemática f entre dos espacios vectoriales U y V
(espacios vectoriales sobre un cuerpo K (K será para nosotros el conjunto de los números
reales,R)),f : U → V , que cumple las siguientes dos propiedades:
• f (x + y) = f (x) + f (y) ∀x,y ∈ U
• f (kx) = kf (x) ∀k ∈ K, ∀x ∈ U
Estas dos propiedades se suelen compactar en una única y equivalente:
• f (k1x1 + . . . + kn xn ) = k1 f (x1 ) + . . . + kn f (xn ) ∀k1 , . . . , kn ∈ K, ∀x1 , . . . ,xn ∈ U
Que el lector no se asuste si nunca ha estudiado estos conceptos. No vamos a ir mucho más
allá de lo que acabamos de explicar.
Intentemos aclarar este concepto mediante dos clásicos ejemplos de operadores lineales:
derivación e integración de funciones de variable real.
La derivación de funciones de variable real es un operador lineal: se trata de una función
que asocia a cada función derivable de variable real, otra función de variable real, su derivada,
cumpliendo además las dos propiedades de linealidad. En este sentido, se puede decir que la
función de derivación tiene la forma der : U → V donde U es el espacio vectorial de todas
las funciones derivables de variable real, y V es el espacio vectorial de todas las funciones de
127
128
CAPÍTULO 7. TEOREMAS
variable real. El cuerpo K sobre el que se definen ambos espacios U y V es el cuerpo de los
números reales, R, dado que estamos trabajando con funciones de variable real.
¿Cumple la función der las propiedades de linealidad? En efecto: supongamos dos funciones
f y g ambas de variable real y derivables (pertenecientes, por tanto, a U). Supongamos un
numero real k, y por tanto perteneciente al conjunto de escalares K sobre el que se definen los
dos espacios U y V .
• der(f + g) = der(f ) + der(g). Cuando estábamos en el colegio nos explicaron que la
derivada de la suma de dos funciones es igual a la suma de las derivadas de ambas función.
Aquı́ no ofreceremos la demostración. Aclaremos esta propiedad mediante un ejemplo:
f (x) = 3x2 , g(x) = 2x ⇒ der(f + g) = der(3x2 + 2x) = 6x + 2 = der(3x2 ) + der(2x) =
der(f ) + der(g).
• der(kf ) = k ·der(f ). Igualmente, sabemos que la derivada de un número real multiplicado
por una función, es igual al número real multiplicado por la derivada de la función. Por
ejemplo: f (x) = 5x3 , k = 6,2 ⇒ der(kf ) = der(6,2 · 5x3 ) = 6,2 · 15x2 = 6,2 · der(5x3 ) =
k · der(f ).
El operador de derivación es, por tanto, un operador lineal.
El proceso de integración de funciones de variable real en un cierto intervalo real, es un
operador lineal: se trata de una función que asocia a cada función integrable en el intervalo de
integración, un cierto escalar real, la integral definida de la función en el intervalo de integración,
cumpliendo además las dos propiedades de linealidad. Supongamos, por ejemplo, el intervalo
de integración [3,5], las funciones f (x) = 3x2 , g(x) = −4x, ambas integrables en todo R, y el
escalar k = 3,3. Es fácil ver que las dos propiedades de linealidad se verifican en este caso:
Z 5
Z 5
Z 5
Z 5
2
2
•
(f (x) + g(x))dx =
(3x + (−4x))dx = 66 = 98 − 32 =
3x dx +
−4xdx =
3
3
3
3
Z 5
Z 5
f (x)dx +
g(x)dx.
3
•
Z
3
3
5
(kf (x))dx =
Z
3
5
2
(3,3 · 3x )dx = 323,4 = 3,3 · 98 = 3,3
Z
3
5
2
3x dx = k
Z
5
f (x)dx.
3
En general, es fácil demostrar que estas dos propiedades se cumplen para cualesquiera funciones
f y g integrables, y para cualquier escalar k.
¿Cómo se comportan los elementos fundamentales constituyentes de nuestros circuitos, a
saber, resistencias, bobinas y condensadores? ¿Muestran dichos elementos un comportamiento
lineal, como el que acaba de definirse?
Una resistencia es un elemento electrónico que cumple que relación que existe entre la
corriente que la atraviesa desde su extremo a hacia su extremo b está relacionada con la tensión
entre a y b del siguiente modo:
V
I=
R
Donde se sobreentiende que la diferencia de tensión V se mide en el sentido de circulación
de I. Más formalmente se puede decir que la resistencia, a cada valor de tensión V entre sus
terminales, le asocia una corriente, según la función I : R → R:
I(V ) =
V
R
Es fácil demostrar que esta función cumple las dos propiedades que hacen que una función sea
considerada lineal:
129
7.1. PRINCIPIO DE SUPERPOSICIÓN
• I(V1 + V2 ) =
propiedad.
• I(kV ) =
V1 + V2 V1 V2
=
+
= I(V1 ) + I(V2 ) ∀V1 ,V2 ∈ R, que es en efecto la primera
R
R
R
V
kV
= k = kI(V ) ∀V, k ∈ R, que es justamente la segunda propiedad.
R
R
Se deduce pues que la función matemática que rige el comportamiento de la resistencia muestra
un comportamiento lineal. Por abuso del lenguaje se dice que la resistencia es un elemento lineal.
Nótese cómo el mismo razonamiento puede ser llevado a cabo considerando que la ecuación que
rige el comportamiento de la resistencia es V (I) = IR. Ambas ecuaciones son equivalentes, y
el resultado de linealidad, por tanto, no se ve alterado.
¿Qué le ocurre a un condensador? Recuérdese que la relación que existe entre la corriente
que atraviesa al condensador desde su extremo a a su extremo b (recuérdese que estrictamente
la corriente no atraviesa al condensador) y la diferencia de tensión existente entre a y b es:
I =C
dV
dt
Donde nuevamente la diferencia de tensión V se ha medido en el sentido de circulación de la
corriente I. De un modo más formal se puede decir que el condensador asocia a cada función
V (t), tensión entre sus terminales, una corriente eléctrica I(t), siguiendo el esquema de una
función I : F → G, donde F es el conjunto de las funciones derivables de variable real (funciones
que en nuestro caso representan la diferencia de tensión entre los extremos del condensador), y
G el conjunto de las funciones de variable real:
I(V ) = C
dV
dt
¿Cumple la función f que rige el comportamiento de un condensador las propiedades de linealidad? Al igual que con el ejemplo de la resistencia, es fácil llegar a la conclusión de que el
condensador es un elemento lineal:
!
d(V1 + V2 )
dV1
dV1 dV2
dV2
• I(V1 +V2 ) = C
=C
=C
+
+C
= I(V1 )+I(V2) ∀V1 , V2 ∈ F ,
dt
dt
dt
dt
dt
que es justamente la primera propiedad.
• I(kV ) = C
dV
d(kV )
= kC
= kI(V ) ∀V ∈ F, ∀ ∈ R, que es la segunda propiedad.
dt
dt
Se deduce pues que el condensador es también un elemento lineal, ya que la función que rige su
comportamiento (función de derivación), cumple las dos condiciones de linealidad. Este mismo
razonamiento se podrı́a haber seguido desde la perspectiva, no de una función que asocia a
cada V (t) un I(t) dado, sino a la inversa: de la ecuación del condensador se puede obtener una
ecuación equivalente que nos da el valor de la tensión que soporta el condensador en función de
la corriente que lo atraviesa (serı́a una función en la que aparecerı́a una integral, en vez de una
derivada). Esta ecuación, igualmente, posee las propiedades de linealidad, ya que es equivalente
a la ecuación que contiene la derivada.
Por último analicemos el comportamiento de una bobina. La tensión que soporta una bobina
entre sus terminales a y b, está relacionada mediante la corriente que la atraviesa desde su
terminal a hasta su terminal b, por la ecuación:
V =L
dI
dt
130
CAPÍTULO 7. TEOREMAS
Donde la diferencia de tensión V se mide en el sentido de circulación de la corriente I. De una
manera más formal, se puede decir que la ecuación que rige el comportamiento de una bobina
está dado por una función V : F → G,donde F es el conjunto de las funciones derivables de
variable real (funciones que en nuestro caso representan la corriente que atraviesa a la bobina
de un extremo a otro), y G el conjunto de las funciones de variable real:
V (I) = L
dI
dt
Esta función muestra un comportamiento lineal, ya que cumple los dos requisitos para que una
función lo sea:
!
d(I1 + I2 )
dI1
dI1 dI2
dI2
• V (I1 + I2 ) = L
=L
=L
+
+L
= V (I1 ) + V (I2 ) ∀I1 ,I2 ∈ F ,
dt
dt
dt
dt
dt
que es la primera condición de linealidad.
dI
d(kI)
= kL
= kV (I) ∀I ∈ F, ∀k ∈ R, que es la segunda condición de
• V (kI) = L
dt
dt
linealidad.
Se deduce pues que la bobina se comporta también como un elemento lineal, ya que la función
que rige su comportamiento es una función lineal.
Se puede demostrar fácilmente que un circuito formado por resistencias, condensadores, bobinas y fuentes de tensión y corriente, se comporta como un sistema
lineal, consecuencia inmediata del hecho de que los elementos electrónicos estudiados en esta
sección muestran un comportamiento también lineal. Se dice entonces que el circuito es un
circuito lineal.
Pues bien, en teorı́a de circuitos, el principio de superposición establece que, si en un circuito
lineal actúan diversas entradas (diversas fuentes, ya sean de tensión o de corriente), entonces
la salida de circuito (tensión o corriente) es igual a la suma de las salidas que se obtendrı́an
considerando la acción de cada entrada por separado (y anulando todas las demás).
Es interesante aclarar algunos aspectos del principio de superposición.
• La linealidad de los elementos estudiados, y por tanto la de un circuito lineal, se aplica
solamente a tensiones o corrientes. El principio de superposición no se puede aplicar,
por ejemplo, a la potencia consumida por una resistencia: la potencia consumida por una
resistencia sobre la que se aplican 6V de tensión no es la suma de las potencias consumidas
por dos fuentes de 3V , por ejemplo.
• En el contexto del principio de superposición, el término entrada hace referencia a cualquier fuente presente en el circuito.
• En el enunciado del principio se habla de la necesidad de anular entradas. Dependiendo
de si la entrada es una fuente de corriente o una fuente de tensión, se aplican las siguientes
reglas:
1. Si la entrada es una fuente de corriente, ésta se sustituye por un circuito abierto.
2. Si la entrada es una fuente de tensión, ésta se sustituye por un cortocircuito.
• También se hace referencia a considerar la acción de cada entrada (fuente) por separado,
anulando todas las demás. El resultado es entonces igual a la suma de cada uno de los
resultados parciales obtenidos considerando la acción de cada fuente por separado. Por
ejemplo, si en un circuito se tienen tres entradas, consistentes en dos fuentes de tensión,
V1 y V2 , y una de corriente, I, una salida cualquiera del circuito, por ejemplo la tensión
7.1. PRINCIPIO DE SUPERPOSICIÓN
131
Vo existente en un determinado punto A, se podrı́a obtener como la suma de la diferentes
salidas Voi obtenidas en los siguientes circuitos:
1. Uno en el que sólo se mantiene la fuente V1 y se anulan tanto a V2 como a I. Se
obtendrı́a un valor de tensión parcial Vo1 en el punto A.
2. Otro en el que se mantiene solamente a la fuente de tensión V2 , anulando a las fuentes
V1 e I. Se obtendrı́a un valor de tensión parcial Vo2 en el punto A.
3. Un último circuito en el que se mantiene la fuente de corriente I y se anulan las dos
fuentes de tensión, V1 y V2 . Se obtendrı́a un último valor de tensión parcial Vo3 en el
punto A.
El valor de tensión Vo buscado en el circuito original, la salida, se obtendrı́a entonces como
la suma de cada una de las salidas parciales obtenidas, es decir:
Vo = Vo1 + Vo2 + Vo3
Cuando se aplica el principio de superposición no es estrictamente necesario considerar
que actúa cada una de las distintas fuentes (entradas) por separado, como acabamos de
hacer nosotros. En cada uno de los sistemas parciales que se resuelven se pueden anular
tantas fuentes como se quieran, no siendo necesario anularlas todas menos a una. El único
requisito es que, de entre todos los sistemas resueltos, no se hayan repetido fuentes en
ninguno de ellos, es decir, que no haya ninguna fuente que haya permanecido activa en
más de un subsistema. Al final, cada fuente debe haber contribuido una y sólo una vez
(es decir, al menos una vez, pero no más de una).
De este modo, el ejemplo de antes se podrı́a haber resuelto de muchos modos. Uno de
ellos, considerando la resolución de cada uno de los siguientes subcircuitos:
1. Uno en el que están activas las dos fuentes de tensión V1 y V2 , anulando a la fuente
de corriente I. Se obtendrı́a un valor parcial de tensión Vo1 .
2. Otro en el que está activa la fuente de corriente I, anulando ambas fuentes de tensión
V1 y V2 . Se obtendrı́a un valor parcial de tensión Vo2 .
Es importante notar que todas las fuentes se encuentran activas en un solo circuito, y
ninguno más. El valor de tensión final serı́a la suma de los valores de tensión parciales
hallados:
Vo = Vo1 + Vo2
Otra posible alternativa para obtener el valor de tensión Vo mediante el principio de
superposición serı́a:
1. Obtener un subcircuito en que se anula la fuente de tensión V2 y se dejan activas
tanto a la fuente de tensión V1 como a la fuente de corriente I. Se obtendrı́a un valor
de tensión parcial Vo1 .
2. Obtener un subcircuito en que se anulan las fuentes V1 e I, dejando activa sólo a la
fuente de tensión V2 . Se obtendrı́a un valor de tensión parcial Vo2 .
El valor de tensión Vo se obtendrı́a como la suma de los diferentes valores de tensión
parciales obtenidos:
Vo = Vo1 + Vo2
Es importante hacer ver, nuevamente, que cada fuente sólo ha contribuido una única vez
al resultado: toda fuente aparece activa en un y sólo un circuito. Ni uno más, ni uno
menos.
132
CAPÍTULO 7. TEOREMAS
1KΩ
V1=10V
Vo
1KΩ
1KΩ
V2=20V
1KΩ
Ig=10mA
Figura 7.1: un ejemplo a resolver mediante el principio de superposición
Para comprender mejor el principio de superposición ası́ como su utilidad en la resolución
de circuitos, vamos a resolver un circuito de principio a fin.
Supongamos el circuito de la Figura 7.1. Para dicho circuito, se pide obtener el valor de la
tensión Vo mediante el principio de superposición.
El circuito de la Figura 7.1 consta de tres fuentes o entradas, dos de tensión y una de
corriente. El principio de superposición puede aplicarse de muy diversas maneras para resolver
el circuito. Se podrı́a seguir, por ejemplo, alguno de los tres caminos siguientes (si bien existen
más):
• Camino 1:
1. Hallar Vo anulando V1 e Ig .
2. Hallar Vo anulando V2 e Ig .
3. Hallar Vo anulando V1 y V2 .
4. El valor de Vo del circuito original serı́a igual a la suma de estos tres valores parciales
de Vo .
• Camino 2:
1. Hallar Vo anulando V1 .
2. Hallar Vo anulando V2 e Ig .
3. El valor de Vo del circuito original serı́a igual a la suma de estos dos valores parciales
de Vo .
• Camino 3:
1. Hallar Vo anulando Ig .
2. Hallar Vo anulando V1 y V2 .
3. El valor de Vo del circuito original serı́a igual a la suma de estos dos valores parciales
de Vo .
Qué camino elegir para resolver el circuito es una decisión que se debe tomar pensando en
cuál va a permitirnos mayores facilidades. Nosotros, por ejemplo, vamos a elegir el camino 3.
Supongamos que anulamos las dos fuentes de tensión V1 y V2 , y que sólo dejamos activa a
la fuente de corriente Ig . Recuérdese que una fuente de tensión se anula sustituyéndola por un
cortocircuito, obteniéndose el circuito de la Figura 7.2.
133
7.1. PRINCIPIO DE SUPERPOSICIÓN
1KΩ
Vo1
1KΩ
1KΩ
1KΩ
Ig=10mA
Figura 7.2: las fuentes de tensión son anuladas sustituyéndolas por cortocircuitos
1KΩ
A
Vo1
1KΩ
1KΩ
+
I1
-
Vg
Ig=10mA
I2
1KΩ
I3
Figura 7.3: corrientes de malla asignadas al circuito
Tras anular las fuentes de tensión, vamos a obtener el valor de tensión Vo para este circuito,
al cual hemos llamado Vo1 . Usaremos el método de las mallas para resolver el circuito. Se trata
de un circuito con una fuente de corriente; por tanto, a ésta se le debe asignar un valor de
tensión (Vg ) y una polaridad. La Figura 7.3 muestra el circuito con las corrientes de malla
asignadas ası́ como con la fuente de corriente con la polaridad asignada.
Las ecuaciones de malla que se obtienen del circuito de la Figura 7.3 son las siguientes:
Vg = 1000I1 − 1000I2
−Vg = I2 (1000 + 1000 + 1000) − 1000I1 − 1000I3
0 = I3 (1000 + 1000)
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
Además, de la fuente de corriente necesitamos obtener otra ecuación para resolver el sistema.
Si suponemos que la corriente I, que circula por la rama de la fuente de corriente, circula hacia
arriba, entonces su expresión según las corrientes de malla es:
I = I1 − I2
Pero es que, además, esa corriente I coincide con la corriente que inyecta la fuente de corriente,
es decir, se tiene:
I1 − I2 = 10 · 10−3
Resolviendo el sistema de ecuaciones formado por las ecuaciones de malla y esta última ecuación,
se tiene:
I1 = 10 · 10−3 A, I2 = 0A, I3 = 0A, Vg = 10V
Nótese que I2 es la corriente que cruza la resistencia de 1KΩ comprendida entre los puntos A
y el punto de Vo . Se tiene por tanto que:
I2 =
Vo − VA
1000
134
CAPÍTULO 7. TEOREMAS
1KΩ
V1=10V
Vo2
1KΩ
1KΩ
V2=20V
1KΩ
Figura 7.4: las fuente de corriente se anula sustituyéndola por un circuito abierto
1KΩ
Vo2
1KΩ
V1=10V
V2=20V
1KΩ
Figura 7.5: la rama de la fuente de corriente se transforma en un circuito abierto
Como justamente I2 = 0, obtenemos:
0=
VA − Vo1
⇔
1000
VA = Vo1
Como además, el punto A está cortocircuitado con la toma de tierra, se obtiene que:
Vo1 = 0V
Nótese cómo se podrı́an haber asociado en paralelo las dos resistencias de la derecha para
simplificar la resolución del circuito (eso nos habrı́a eliminado una malla).
Ahora supongamos que anulamos la fuente de corriente Ig y que dejamos activas a las dos
fuentes de tensión V1 y V2 . El circuito que resulta tras sustituir la fuente de corriente por un
circuito abierto es el de la Figura 7.4.
Ahora pensemos un poco en lo que a este circuito respecta. La rama donde se situaba la
fuente de corriente contiene ahora un circuito abierto (resistencia de valor infinito), conectado
en serie con una resistencia de 1KΩ. Podemos asociar ambas resistencias en serie, obteniendo
una resistencia de valor, obviamente, infinito, es decir, otro circuito abierto. Se obtiene entonces
el circuito de la Figura 7.5.
La rama donde se situaba la fuente de corriente, por tanto, se transforma en un circuito
abierto. A efectos prácticos, la presencia de una rama con un circuito abierto puede ser ignorada
en el análisis del circuito, ya que por dicha rama no va a circular ninguna corriente. Por tanto,
la rama es omitida, quedando un circuito como el de la Figura 7.6.
El circuito resultante lo resolveremos mediante el método de las mallas. El circuito consta
de dos mallas, a las que les asignamos corrientes de malla tal y como indica la Figura 7.7.
Las ecuaciones de malla que se obtienen del circuito son las siguientes:
10 = I1 (1000 + 1000) − 1000I2
−20 = I2 (1000 + 1000) − 1000I1
(Malla de I1 )
(Malla de I2 )
135
7.1. PRINCIPIO DE SUPERPOSICIÓN
1KΩ
Vo2
1KΩ
V1=10V
V2=20V
1KΩ
Figura 7.6: el circuito resultante tras anular la fuente de corriente
A
1KΩ
Vo2
1KΩ
V1=10V
V2=20V
1KΩ
I1
I2
Figura 7.7: circuito con las corrientes de malla asignadas
De la resolución del sistema de ecuaciones se obtiene:
I1 = 0A, I2 = −0,01A
Ahora bien, I1 es la corriente que atraviesa la resistencia que hay entre el punto A y el punto
de Vo 2, y por tanto puede reescribirse, según la Ley de Ohm, como:
I1 =
VA − Vo2
1000
Como I1 = 0:
VA − Vo2
=0⇔
1000
VA = Vo2
Como justamente VA = 10V según dicta la fuente de tensión de la izquierda, se deduce:
Vo2 = 10V
Ya tenemos los resultados parciales de Vo para cada circuito. Para obtener el valor de Vo del
circuito original, basta sumar ambos valores parciales de Vo , es decir:
Vo = Vo1 + Vo2 = 0 + 10 = 10V
Se deja al lector, como ejercicio, comprobar que este valor de Vo es el que se obtiene resolviendo
el circuito original.
El principio de superposición hay que aplicarlo con inteligencia. En el ejemplo que hemos
resuelto, no ha supuesto un menor esfuerzo. Sin embargo, cuando se elige un camino para la
resolución de un circuito mediante el principio de superposición, se busca que los subcircuitos
136
CAPÍTULO 7. TEOREMAS
Rt
A
Circuito lineal
B
A
Vt +
−
B
Figura 7.8: teorema de Thevènin
obtenidos sean de una resolución más sencilla que la del circuito original. Por ejemplo, cuando
hemos anulado la fuente de corriente dejando activas las dos de tensión, hemos obtenido un
circuito con una rama menos, que nos ha simplificado el análisis. En general, antes de aplicar el
principio de superposición a lo loco, se recomienda analizar los subcircuitos que se obtendrı́an,
para ver si éstos son más sencillos que el original (bien por la desaparición de alguna rama
en la que habı́a una fuente de corriente, bien porque al sustituir una fuente de tensión por un
cortocircuito se pueden llevar a cabo asociaciones de elementos que antes no se podı́a, etc.).
7.2.
Teorema de Thévenin
El fundamento de las asociaciones (sección 4.1) era el de intentar simplificar distribuciones
de elementos por otros equivalentes, de modo que se simplificase el análisis del circuito donde
se situasen dichos elementos.
El problema de las asociaciones, tal y como fueron concebidas, es que sólo permitı́an asociar
elementos de un mismo tipo entre sı́: resistencias con resistencias, fuentes de tensión con fuentes
de tensión, condensadores con condensadores, etc.. Desde este punto de vista, las asociaciones
de elementos son una herramienta bastante limitada a la suerte que se pueda tener a la hora
de resolver un circuito: si el circuito permite asociaciones, pues se asocia, y si no, pues nos
aguantamos.
El teorema de Thevènin viene a resolvernos este gran problema. Thevènin, a diferencia de los
métodos de asociaciones clásicos, permite condensar cualquier subcircuito en otro equivalente.
Nosotros vamos a enunciar el teorema de Thevènin dentro del análisis de circuitos de corriente
continua, donde bobinas y condensadores se transforman en cortocircuitos y circuitos abiertos
respectivamente (los cuales son casos extremos de resistencias, como se explicó en la sección
2.1). El teorema de Thevènin puede generalizarse para circuitos con bobinas y condensadores
fuera del marco de los circuitos de corriente continua; en dichos circuitos, condensadores y
bobinas no se transforman en casos extremos de resistencias, sino que se mantienen vivitos
y coleando. A pesar de ello, nosotros restringiremos el teorema, por ahora, a los circuitos de
corriente continua, donde se puede decir que todo se reduce a resistencias, fuentes de tensión
y fuentes de corriente. En un futuro no muy lejano (en la siguiente entrega de esta magnı́fica
colección titulada Introducción a la teorı́a de circuitos), ampliaremos el teorema, contemplando
otros dominios a parte del de la corriente continua.
El teorema de Thevènin dice ası́:
Todo circuito lineal con dos terminales puede sustituirse por un modelo equivalente, formado por una fuente de tensión de valor Vt conectada en serie a una
resistencia de valor Rt .
Chachi. El teorema de Thevènin nos está diciendo que no importa cuán complicado pueda
ser un circuito con dos terminales externos, pues éste es equivalente a un modelo formado por
una fuente de tensión y una resistencia en serie. Concretamente, se tiene una equivalencia como
la de la Figura 7.8.
Donde los tan ansiados valores de Vt y Rt se obtienen del siguiente modo:
137
7.2. TEOREMA DE THÉVENIN
1KΩ
10V
1KΩ
A
5KΩ
3KΩ
B
Figura 7.9: circuito que resolveremos usando el teorema de Thevènin
• Vt , tensión Thevènin, es la tensión que se mide entre A y B en el circuito original,
cuando ambos terminales se dejan en circuito abierto. Es decir, Vt = VAB = VA − VB .
• Rt , resistencia Thevènin, es la resistencia equivalente que se mide entre A y B cuando
todas las fuentes del circuito original han sido anuladas (las de tensión se sustituyen por
un cortocircuito, y las de corriente, por un circuito abierto). Si la resistencia no se puede
obtener por los métodos convencionales de asociaciones en serie y en paralelo, se recurrirı́a
al método general.
Es de especial interés destacar dos aspectos de la Figura 7.8. El primero es que la resistencia
Thevènin puede colocarse tanto conectada al polo positivo de la fuente de tensión Thèvenin,
como se muestra en la Figura 7.8, como al polo negativo; nosotros, por costumbre, la colocaremos conectada al polo positivo de la fuente de tensión Thevènin. El segundo está relacionado
en el modo en el que se coloca la polaridad de la fuente de tensión Thevènin. Siempre se pueden
obtener dos tensiones Thevènin. Supongamos que tenemos un circuito con dos terminales externos, que decidimos denominar M y Z (prefiero rehuir a los clásicos A y B). En este caso
se podrı́a obtener tanto la tensión Thevènin Vt = VM Z = VM − VZ como la tensión Thevènin
Vt = VZM = VZ − VM . El detalle importante es que el polo positivo de la fuente de tensión
Thevènin debe estar orientado hacia el primer punto sobre el que se mide la diferencia de tensión, y el polo negativo, hacia el segundo punto sobre el que se mide la diferencia de tensión. En
el caso de, por ejemplo, de haber medido la tensión Thevènin VZM = VZ − VM , el polo positivo
deberı́a colocarse más cerca del terminal Z que del terminal M, y el polo negativo, más cerca
del terminal M que del terminal Z. En el caso de la Figura 7.8, la tensión Thevènin medida es
la tensión entre A y B, dado que el polo positivo de la fuente de tensión Thevènin está más
cerca de A que de B, y el negativo está más cerca de B que de A.
Otro aspecto muy importante a tener en cuenta es que, tras sustituir el circuito original por
su equivalente Thevènin, los terminales externos, los puntos A y B, siguen existiendo, de modo
que cualquier parámetro asociado a dichos puntos podrı́a seguir midiéndose en el circuito con
el modelo Thevènin.
Supongamos por ejemplo el circuito de la Figura 7.9, en el que se nos pide obtener la
diferencia de tensión que existe entre los puntos A y B, es decir, VAB = VA − VB .
¿Cómo podemos sacar partido del teorema de Thevènin a la hora de resolver este circuito?
Se nos está pidiendo la tensión que existe entre los puntos A y B. Podrı́amos intentar simplificar
el circuito que se ve desde los puntos A y B, y hacia la izquierda. Obteniendo el equivalente
Thevènin de ese circuito, el análisis del circuito se simplificarı́a bastante. Nótese cómo, además,
si se sustituye ese subcircuito por su equivalente Thevènin, los terminales A y B seguirı́an existiendo en el modelo simplificado, y por tanto la tensión entre A y B podrı́a medirse igualmente
en el modelo simplificado con Thevènin que en el circuito original.
El subcircuito del que se quiere obtener el equivalente Thevènin es el circuito representado
en la Figura 7.10.
138
CAPÍTULO 7. TEOREMAS
C
1KΩ
1KΩ
D
I1
10V
A
I3
I2
5KΩ
B
Figura 7.10: ¡se busca el Thevènin!
Para hallar el equivalente Thevènin del circuito de la Figura 7.10, hay que obtener tanto la
tensión Thevènin como la resistencia Thevènin.
La tensión Thevènin es la tensión que se mide entre los puntos A y B (podrı́a medirse la que
hay entre los terminales B y A, pero optamos por medir la que hay entre A y B). Para simplificar
el análisis, se ha colocado la toma de tierra conectada a B, para que ası́ la tensión Thevènin
sea simplemente la tensión en el punto A: Vt = VAB = VA − VB = VA − 0 = VA . Recuérdese
que colocar una toma de tierra no hace que varı́en las diferencias de tensión existentes entre
cualesquiera puntos del circuito.
En el circuito de la Figura 7.10 podemos aplicar el método de los nudos para su resolución.
Obsérvese, sin embargo, que la corriente I3 ha de ser una corriente nula, dado que la rama de I3
es una rama acabada en un circuito abierto (no está conectada a nada), y por ella, por tanto,
no puede circular corriente. Se tiene que, por tanto que I3 = 0. Se puede usar la expresión de
la Ley de Ohm de I3 para deducir, además, que:
I3 =
VD − VA
=0⇔
1000
VD = VA
Del nudo D se puede deducir fácilmente que I1 = I2 , ya que I3 = 0. Sustituyendo las corrientes
por sus expresiones según la Ley de Ohm, y considerando que VB = 0 por estar conectado a
tierra y que VC = 10 según la fuente de tensión:
I1 = I2 ⇔
VC − VD
VD − VB
=
⇔
1000
5000
10 − VD
VD
=
⇔
1000
5000
25
VD = V
3
Como la tensión en D coincide con la tensión en A, se tiene por tanto que:
Vt = VAB =
25
V
3
Nótese que este circuito se comporta como un divisor de tensión. En efecto, al no circular
corriente por la rama de I3 , es como si ésta no existiera, y se tiene que la tensión en D es:
25
5000
5000
= 10 ·
= V
VD = VC ·
5000 + 6000
5000 + 6000
3
Que es justamente la que obtuvimos anteriormente, pero sin tanta complicación. Obsérvese,
insisto, en cómo este circuito se ha reducido a un simple divisor de tensión.
139
7.2. TEOREMA DE THÉVENIN
1KΩ
1KΩ
A
5KΩ
B
Figura 7.11: conjunto de resistencias tras anular las fuentes del circuito
A
Req=5500/3Ω
B
Figura 7.12: resistencia Thevènin
Nos queda obtener la resistencia Thevènin Rt , que es la resistencia equivalente que se mide
entre A y B cuando se anulan todas las fuentes del circuito.
Al anular las fuentes internas del circuito, la fuente de tensión se transforma en un cortocircuito, de modo que nos queda el conjunto de resistencias de la Figura 7.11.
La resistencia equivalente medida entre los terminales A y B del circuito es trivial. Fijémonos
en que las dos resistencias de la izquierda, la de 1KΩ y la de 5KΩ están conectadas en paralelo.
Tras asociarlas, queda una resistencia de 2500/3Ω, que se asocia en serie con la resistencia en
serie restante para dar una resistencia equivalente medida entre A y B de 5500/3Ω(Figura 7.12),
es decir:
5500
Ω
Rt =
3
Obtenidas la tensión Thevènin y la resistencia Thevènin, podemos construir el equivalente
Thevènin (Figura 7.13) del circuito de la Figura 7.10. Es de especial interés notar que la
tensión Thevènin medida fue la existente entre los terminales A y B. Por tanto, el polo positivo
de la fuente de tensión Thevènin va orientado al terminal A, mientras que el polo negativo
va orientado al terminal B. La resistencia podrı́a haberse colocado conectada a uno u otro
terminal, pero optamos por conectarla al terminal A.
Recuérdese que el problema que se nos planteaba era medir la tensión entre A y B en el
circuito original, el de la Figura 7.9. Nosotros hemos decidido simplificar el circuito obteniendo
el equivalente Thevènin del subcircuito que se ve desde los puntos A y B, y hacia la izquierda. Si
Rt=5500/3Ω
A
Vt=25/3V
B
Figura 7.13: el equivalente Thevènin buscado
140
CAPÍTULO 7. TEOREMAS
Rt=5500/3Ω
A
Vt=25/3V
3KΩ
B
Figura 7.14: circuito original, simplificado tras sustituir una de sus partes por el equivalente
Thevènin
1KΩ
10V
1KΩ
Vo
5KΩ
I1
3KΩ
I2
Figura 7.15: el circuito original, resuelto por mallas
ahora sustituimos ese subcircuito por su equivalente Thevènin, el circuito original simplificado
se reduce en gran medida, como se muestra en la Figura 7.14.
Del circuito de la Figura 7.14 se puede obtener la tensión entre A y B colocando una toma
de tierra conectada al punto B. En ese caso, la diferencia de tensión entre A y B coincide con la
tensión que hay en el punto A. Nótese que el circuito de la Figura 7.14 es un divisor de tensión,
donde buscamos la tensión en el punto A. Esa tensión se puede obtener mediante el uso directo
de la fórmula del divisor de tensión:
25
150
3000
VA = VAB =
=
·
V
3
3000 + 5500/3
29
Que es la tensión entre los puntos A y B buscada en el circuito original. Obsérvese cómo al
emplear el equivalente Thevènin para simplificar el circuito original, la resolución del circuito
se ha reducido a dos divisores de tensión.
Podemos comprobar que la resolución directa del circuito de la Figura 7.9 nos habrı́a llevado al mismo resultado que al usar el equivalente Thevènin. Supongamos que resolvemos el
circuito aplicando mallas, como se muestra en la Figura 7.15. Se ha colocado una toma de tierra
conectada al punto B, para que la tensión VAB coincida con la tensión Vo señalada en el circuito
de la figura.
Aplicando el método de las mallas, se obtienen las dos siguientes ecuaciones:
10 = I1 (1000 + 5000) − 5000I2
0 = I2 (5000 + 1000 + 3000) − 5000I1
(Malla de I1 )
(Malla de I2 )
Del sistema de ecuaciones de malla se obtiene, trivialmente:
I1 =
1
9
A, I2 =
A
2900
580
Observemos que la corriente de malla I2 coincide con la que circula por la resistencia de 3KΩ,
141
7.3. TEOREMA DE NORTON
A
A
Circuito lineal
In
B
Rn
B
Figura 7.16: teorema de Norton
y se puede reescribir, según la Ley de Ohm:
Vo
⇔
3000
1
Vo
=
⇔
580
3000
150
V
Vo = VAB =
29
I2 =
Que es justamente el mismo valor de tensión VAB obtenido simplificando el circuito original
mediante Thevènin.
7.3.
Teorema de Norton
El teorema de Norton es un teorema análogo al de Thevènin, en el sentido de que nos permite
simplificar cualquier circuito lineal, sustituyéndolo por un modelo equivalente formado por una
fuente y una resistencia. La diferencia es que, en teorema de Norton, la fuente empleada es una
fuente de corriente, y la resistencia se coloca en paralelo a la fuente de corriente. Concretamente,
el teorema de Norton dice ası́:
Todo circuito lineal con dos terminales puede sustituirse por un modelo equivalente, formado por una fuente de corriente de valor In conectada en paralelo a una
resistencia de valor Rn .
El teorema de Norton nos está diciendo que no importa cuán complicado pueda ser un
circuito con dos terminales externos, pues éste es equivalente a un modelo formado por una
fuente de corriente y una resistencia en paralelo. Concretamente, se tiene una equivalencia como
la de la Figura 7.16.
Donde los tan ansiados valores de In y Rn se obtienen del siguiente modo:
• In , corriente Norton, es la corriente que circula por el cortocircuito del terminal A
al terminal B, cuando estos han sido cortocircuitados.
• Rn , resistencia Norton, es una resistencia de valor igual a la resistencia Thevènin, es decir,
Rn = Rt .
Respecto a la corriente Norton, ésta se obtiene como la corriente que circula por el cortocircuito creado entre los terminales A y B del circuito original. Es importante notar que, si la
corriente Norton medida es la que circula de A a B, entonces la fuente de corriente del modelo
Norton equivalente (Figura 7.16) apunta, de algún modo, de B a A, tal y como se muestra en
la Figura 7.16. En cambio, si la corriente Norton que se mide como la corriente que circula de
B a A, entonces la fuente de corriente Norton del modelo equivalente debe colocarse orientada
de A a B
142
CAPÍTULO 7. TEOREMAS
C
1KΩ
1KΩ
D
I1
A
I3
10V
I2
5KΩ
B
Figura 7.17: terminales A y B cortocircuitados para obtener la corriente Norton
Supongamos que se nos pide obtener el equivalente Norton del circuito de la Figura 7.10, que
es el circuito del que anteriormente obtuvimos el equivalente Thevènin. El valor de la resistencia
Norton ya lo conocemos, pues el mismo valor que el de la resistencia Thevènin, y por tanto:
Rn =
5500
Ω
3
La corriente Norton es la corriente que circula del terminal A al terminal B cuando ambos
terminales están cortocircuitados (podrı́a haberse decidido medir la corriente que circula de
B a A, pero hemos optado por medir la corriente que va de A a B). La Figura 7.17 muestra
el circuito con los terminales A y B cortocircuitados. Para resolver el circuito se empleará el
método de los nudos. La Figura 7.17 muestra corrientes asignadas a cada rama para aplicar el
método de los nudos, que será empleado en el nudo D. Obsérvese cómo la corriente I3 coincide
con la corriente que circula de A a B, los terminales del circuito cortocircuitados. Por tanto, la
corriente I3 coincide con la corriente Norton buscada.
La ecuación del nudo D es la siguiente:
I1 = I2 + I3
Si sustituimos cada corriente pro su expresión según la Ley de Ohm:
VD − VB VD − VA
VC − VD
=
+
1000
5000
1000
Además, VC = 10, VB = VA = 0, y por tanto:
VD
VD
10 − VD
=
+
1000
5000 1000
De donde
VD =
Y por tanto:
50
V
11
1
VD
=
A
1000
220
Y por tanto el circuito equivalente Norton es el de la Figura 7.18.
Podemos usar ahora este equivalente Norton para, en efecto, ver que el valor de tensión
existente entre los puntos A y B del circuito de la Figura 7.9 es el mismo que el obtenido
cuando se usó el equivalente Thevènin, como serı́a de esperar. La Figura 7.19 muestra el circuito
original (el de la Figura 7.9), donde se ha sustituido todo el subcircuito visto desde los puntos
A y B, y hacia la izquierda, por su respectivo equivalente Norton. Usando el método de los
nudos para resolverlo, se deduce, del nudo C, que:
In = I3 =
143
7.4. RELACIÓN THEVÈNIN-NORTON
A
In=1/220A
Rn=5500/3Ω
B
Figura 7.18: equivalente Norton buscado
C
A
I3
In=1/220A
I1 I2
Rn=5500/3Ω 3KΩ
B
Figura 7.19: cómo obtener la tensión entre A y B en el circuito original
I1 = I2 + I3
Teniendo en cuenta que la corriente I1 coincide con la corriente que inyecta la fuente de corriente,
y sustituyendo las otras corrientes por sus expresiones según la Ley de Ohm:
1
VAB
VAB
=
+
220
5500/3 3000
Nótese cómo, a diferencia de como solemos aplicar la Ley de Ohm, en este caso podemos usar
la incógnita VAB en vez de VA − VB para cada corriente, y ası́ resolver directamente el circuito
sin necesidad de colocar una toma de tierra. El valor de VAB obtenido de la ecuación anterior
es:
150
V
VAB =
29
Que es justamente la tensión VAB que obtuvimos cuando empleamos el equivalente Thevènin.
7.4.
Relación Thevènin-Norton
Cuando se pretende simplificar un circuito mediante el teorema de Thevènin o el teorema
de Norton, podemos encontrarnos en el dilema de cuál de ellos emplear. Esta cuestión, sin
embargo, no tiene demasiada importancia, como ahora veremos.
Hemos visto cómo Thevènin y Norton permiten obtener un modelo equivalente asociado
a cualquier circuito lineal con dos terminales externos. El que ambos teoremas sean universalmente aplicables nos conduce a la siguiente pregunta: ¿por qué no aplicar el mismo teorema
de Norton a un circuito equivalente de Thevènin para obtener ası́ el equivalente de Norton
asociado a un circuito equivalente de Thevènin? O a la inversa, ¿por qué no aplicar el teorema
de Thevènin a un circuito equivalente de Norton para ası́ obtener el equivalente de Thevènin
asociado a un circuito equivalente de Norton?
La idea que hay detrás de estas preguntas es la misma: dado un equivalente de Thevènin o
de Norton, obtener el equivalente de Norton y de Thevènin asociado respectivamente. ¿Existe
alguna relación matemática, a ser posible sencilla, que nos permita transformar un equivalente
Thevènin en un equivalente Norton, y a la inversa? La respuesta es sı́, y se puede deducir
fácilmente aplicando el mismo teorema de Norton a un circuito equivalente de Thevènin genérico
144
CAPÍTULO 7. TEOREMAS
Rt
A
Vt +
−
B
Figura 7.20: equivalente Thevènin genérico
Rt
Vt +
−
A
In
B
Figura 7.21: hallando el equivalente Norton de un Thevènin genérico
(podrı́a hacerse al revés: aplicar el teorema de Thevènin a un equivalente de Norton genérico).
La idea es obtener el equivalente Norton de un circuito equivalente Thevènin general, de modo
que podamos transformar uno en otro rápidamente, sin necesidad de tener que obtenerlo del
circuito original (lo cual puede ser complicado). Supongamos el circuito equivalente de Thevènin
genérico de la Figura 7.20.
¿Cuál es equivalente Norton asociado a ese equivalente Thevènin genérico? Para obtenerlo,
podemos proceder tal y como se explicó en la sección 7.3.
La corriente Norton es la corriente que circula del terminal A al terminal B cuando ambos
terminales han sido cortocircuitados (Figura 7.21).
Del circuito de la Figura 7.21 se deduce que la corriente Norton del equivalente Thevénin
genérico toma la expresión:
Vt
In =
Rt
¿Cómo obtener la resistencia Norton asociada? Recuérdese que la resistencia Norton se obtiene
del mismo modo que la resistencia Thevènin: se anulan las fuentes internas y se obtiene la
resistencia medida entre los dos terminales externos. Si anulamos la única fuente interna, que
es la fuente de la resistencia Thevènin, sustituyéndola por un cortocircuito, el circuito que
nos queda consiste en una única resistencia de valor Rt , cuyos terminales coinciden con los
terminales externos A y B. La resistencia Norton asociada, por tanto, es igual a Rt :
Rn = Rt
Se deduce pues que el equivalente Norton asociado a uno Thevènin de tensión Thevènin Vt
y resistencia Thevènin Rt es uno formado por una fuente de corriente de valor Vt /Rt , y de
resistencia Norton igual a la resistencia Thevènin Rt . Tenemos una equivalencia, por tanto,
como la de la Figura 7.22.
Todo circuito lineal es equivalente a un modelo Thevènin y a un modelo Norton,
y a su vez, estos son equivalentes entre sı́, siendo la relación existiente entre ellos
Rt
A
Circuito lineal
B
A
Vt +
−
In=Vt/Rt
Rn=Rt
A
In
B
Figura 7.22: relación existente entre los modelos de Thevènin y de Norton
Rn
B
145
7.4. RELACIÓN THEVÈNIN-NORTON
la dada por las ecuaciones:
Rn = Rt
Vt
In =
Rt
(7.1)
(7.2)
Podemos comprobar que esta relación, en efecto, se cumple en los equivalentes Thevènin y
Norton que obtuvimos anteriormente. El equivalente Thevènin obtenido en la sección 7.2 tenı́a,
como parámetros caracterı́sticos, los siguientes:
25
V
3
5500
Rt =
Ω
3
Vt =
A su vez, el equivalente Norton obtenido en la sección 7.3, obtenido del mismo circuito que el
de la sección 7.2, tenı́a, como parámetros caracterı́sticos:
1
A
220
5500
Ω
Rn =
3
In =
Se puede comprobar fácilmente que la relación existente entre el equivalente de Thevènin y de
Norton de ambos circuitos es la que justamente acabamos de hallar (ecuaciones (7.1) y (7.2)):
In =
Vt
Rt
Ya que:
25/3
1
=
220
5500/3
Además, las resistencias de Thevènin y de Norton son iguales.
Se aprecia pues que, dado un equivalente Thevènin o un equivalente Norton, obtener el
equivalente simétrico (Norton y Thevènin respectivamente) es una tarea trivial, pues la relación
existente entre los modelos Thevènin y Norton de un circuito dado viene dada por las dos
ecuaciones Rn = Rt y In = Vt /Rt . Ası́ por ejemplo, sabiendo las relaciones existentes entre
el equivalente Norton y el equivalente Thèvenin, el Norton de la sección 7.3 se podrı́a haber
obtenido directamente del Thèvenin de la sección 7.2 haciendo uso de las ecuaciones In =
Vt /Rt = (25/3)/(5500/3) = 1/220A ası́ como Rn = Rt = 5500/3Ω.
En general, se puede decir que una fuente de tensión de valor V conectada a una resistencia
en serie de valor R, se puede sustituir por una fuente de corriente de valor V /R conectada a una
resistencia en paralelo de valor R. A la inversa, una fuente de corriente de valor I conectada a
una resistencia en paralelo de valor R, puede sustituirse por una fuente de tensión de valor IR,
conectada a una resistencia en serie de valor R. Todo esto se resume en la Figura 7.22. Cuando
una fuente de corriente se transforma en una de tensión, o a la inversa, tal y como se muestra
en la Figura 7.22, es importante preservar la orientación de las fuentes: si la fuente de tensión
tiene su polo positivo apuntando hacia un extremo, digamos A, entonces la fuente de corriente
por la que se sustituye también debe apuntar hacia A.
Es importante mantener en mente esta última equivalencia: en muchos circuitos hay presentes fuentes de tensión conectadas a resistencias en serie, ası́ como fuentes de corriente conectadas a resistencias en paralelo. Puede convenirnos, en ciertas circunstancias, transformar un
modelo en otro, y viceversa.
146
CAPÍTULO 7. TEOREMAS
7.5.
Teoremas, ejercicios
Ejercicio 7.1: Para el circuito de la Figura 7.23, se pide determinar el equivalente Thevènin
medido entre los terminales A y B.
18mA
2KΩ
A
1KΩ
B
-18V
1KΩ
6KΩ
Figura 7.23: Ejemplo 7.1
Solución
Antes de comenzar propiamente dicho con este ejemplo, quizás sea conveniente remarcar
un pequeño detalle. Quizás resulte extraño que se nos pida el equivalente Thevènin del circuito
de la Figura 7.23. El equivalente Thevènin puede hallarse de todo circuito lineal con dos
terminales externos, tal y como se explicó convenientemente en la sección 7.2. La pregunta
es si en eso de la Figura 7.23, los terminales A y B son, en efecto, terminales externos. Cuando
se habla de terminales externos en el teorema de Thevènin, no nos referimos más que a dos
puntos cualesquiera del circuito. Cualesquiera dos puntos del circuito pueden ser considerados
los terminales externos de los que habla el teorema, y por tanto A y B pueden ser considerados
como tales, a pesar de que no tengan el aspecto de un terminal externo sano y alegre como los
de la Figura 7.8. Esta pequeña parrafadilla no es más que una tonterı́a si se entiende la esencia
del teorema de Thevènin; aun ası́, prefiero dejar claro este detalle, para que no nos llevemos
sorpresas a la hora de hallar ningún Thevènin.
Para obtener el circuito equivalente Thevènin del circuito de la Figura 7.23, debemos hallar
tanto la tensión Thevènin como la resistencia Thevènin. La tensión Thevènin es la que se mide
entre los terminales A y B, es decir, VAB = VA −VB (aunque también se podrı́a haber optado por
medir la tensión VBA = VB − VA , si bien optamos por medir VAB . Recuérdese que, dependiendo
de la tensión medida, la fuente de tensión Thevènin del equivalente estará orientada hacia un
lado u otro (en lo que a polaridad se refiere). La resistencia Thevènin es la que se mide entre
los puntos A y B, tras anular todas las fuentes internas.
Comencemos por la resistencia Thevènin. Tras anular las fuentes del circuito (las de corriente
se sustituyen por circuitos abiertos y las de tensión por cortocircuitos), nos queda un conjunto
de resistencias como el de la Figura 7.24.
Es importante fijarse en el detalle de cómo la rama de la fuente de corriente ha sido directamente suprimida, ya que ésta se transforma en un circuito abierto, y en general, en cualquier
cálculo relacionado con el cálculo de resistencias equivalentes, las ramas donde hay presentes
circuitos abiertos pueden omitirse sin influir en el resultado de la resistencia equivalente buscada.
Comenzamos asociando en paralelo el cortocircuto que está conectado en paralelo a la
resistencia de 1KΩ. El resultado es el de la Figura 7.25.
147
7.5. TEOREMAS, EJERCICIOS
2KΩ
1KΩ
A
B
1KΩ
6KΩ
Figura 7.24: tras anular las fuentes internas
2KΩ
A
1KΩ
B
6KΩ
Figura 7.25: obteniendo la resistencia Thevènin
El siguiente paso es el de asociar las resistencias de arriba, de 2KΩ y 1KΩ, en serie,
obteniéndose otra equivalente de 3KΩ, como se aprecia en la Figura 7.26.
A continuación, y por último, se asocian en paralelo las resistencias de 3KΩ y 6KΩ,
obteniéndose la resistencia Thevènin buscada, de 2000Ω, tal y como se muestra en la Figura 7.27. Obsérvese que la resistencia Thevènin es la medida entre las terminales A y B, y por
tanto, las asociaciones llevadas a cabo durante el proceso de su obtención no pueden eliminar
a ninguno de esos dos puntos.
Tenemos pues que:
Rt = 2000Ω
Para obtener la tensión Thevènin, calculamos la diferencia de tensión entre A y B en el circuito
original (Figura 7.23). La Figura 7.28 muestra las corrientes asignadas a las ramas del circuito
para su resolución mediante el método de los nudos. Las ecuaciones obtenidas son:
I1 + I2 = I3
I3 = I4
(Nudo C)
(Nudo B)
Obsérvese cómo la ecuación del nudo B es un tanto aplatanadamente estúpida. La ecuación
del nudo B nos dice que las corrientes I3 e I4 son iguales; obviamente es ası́, dado que ambas
corrientes circulan por la misma rama. Esa ecuación viene a decirnos, pues, que dicha corriente
puede escribirse de dos modos, uno como la corriente que atraviesa la resistencia de 6KΩ y
otro como la corriente que atraviesa la resistencia de 1KΩ.
Si sustituimos cada corriente por su valor dado por la Ley de Ohm, y consideramos que
148
CAPÍTULO 7. TEOREMAS
3KΩ
A
B
6KΩ
Figura 7.26: obteniendo la resistencia Thevènin
A
2000Ω
B
Figura 7.27: resistencia Thevènin
C
I1
18mA
I2
I3
2KΩ
A
1KΩ
B
-18V
1KΩ
6KΩ
I4
Figura 7.28: obteniendo la tensión Thevènin
149
7.5. TEOREMAS, EJERCICIOS
2KΩ
A
-30V
B
Figura 7.29: el equivalente Thevènin buscado
según la fuente de tensión VA = −18 y que según la de corriente I1 = 18 · 10−3 , obtenemos:


−3
I
=
18
·
10
1








V
−
V
A
C





I
=

 2


− 18 − VC
VC − VB



2000
18 · 10−3 +


=
VC − VB
2000
1000
⇒
I3 =
VB
VC − VB



1000





=


VB


1000
6000




I
=
4




6000


VA = −18
De donde:
VB = 12V, VC = 14V
La tensión Thevènin es la medida entre A y B, y por tanto:
Vt = VA − VB = −18 − 12 = −30V
El equivalente Thevènin que se obtiene es, por tanto, el de la Figura 7.29. Obsérvese cómo la
fuente de tensión Thevènin, de valor −30V , está orientada con el polo positivo hacia el terminal
A, y el negativo hacia el B. Esto se debe, recordemos, a que hemos hallado la tensión Thevènin
VAB . Si hubiéramos hallado la tensión VBA , la polaridad de la fuente de tensión deberı́a estar
invertida.
Ejercicio 7.2: Calcular el circuito equivalente Thevènin del circuito de la Figura 7.30, medido
entre los terminales A y B. A partir de él, obtener el equivalente Norton.
1KΩ
1KΩ
A
1mA
5V
1KΩ
1KΩ
B
Figura 7.30: Ejemplo 7.2
Solución
150
CAPÍTULO 7. TEOREMAS
1KΩ
1KΩ
A
1KΩ
1KΩ
B
Figura 7.31: obteniendo la resistencia Thevènin
1KΩ
A
1KΩ
1KΩ
B
Figura 7.32: obteniendo la resistencia Thevènin
En primer lugar obtenemos la resistencia Thevènin. La resistencia Thevènin es la resistencia
equivalente que se mide entre los terminales A y B, cuando se han anulado todas las fuentes
internas. Tras sustituir la fuente de corriente por un circuito abierto y la de tensión por un
cortocircuito, nos queda el conjunto de resistencias de la Figura 7.31.
El circuito abierto de la izquierda puede asociarse en serie con la resistencia de 1KΩ que
está situada en su misma rama, quedando como resultado otro circuito abierto, tal y como se
muestra en la Figura 7.32.
Por último, se puede asociar en paralelo el circuito abierto con la resistencia de 1KΩ a la
que está conectada, quedando el conjunto de resistencias de la Figura 7.33.
De la Figura 7.33 se puede apreciar que, tal y como se dijo en el ejemplo anterior, directamente se podrı́a haber suprimido la rama en la que se situaba la fuente de corriente a la hora
de hallar la resistencia Thevènin: el resultado no se habrı́a visto alterado.
1KΩ
1KΩ
A
1KΩ
B
Figura 7.33: obteniendo la resistencia Thevènin
151
7.5. TEOREMAS, EJERCICIOS
1KΩ
1KΩ
5V
1KΩ
I1
A
1KΩ
I2
B
Figura 7.34: obteniendo la tensión Thevènin
La resistencia equivalente medida entre los terminales A y B es trivial, y su valor es de:
Rt =
2000
Ω
3
La tensión Thevènin es la tensión que se mide entre los terminales A y B (VAB ) del circuito
original. Para obtener la tensión Thevènin vamos a aplicar el principio de superposición. Si bien
en este ejemplo no nos supone una gran ayuda, ası́ lo pondremos en práctica.
Supongamos que sólo actúa la fuente de tensión, anulando la de corriente. El circuito que
nos queda es el de la Figura 7.34, en el que se aprecia que se ha sustituido la fuente de corriente
por un circuito abierto, y donde se ha colocado la toma de tierra conectada a B para que ası́ la
tensión VAB coincida con VA . El circuito será resuelto por mallas. Las ecuaciones de malla que
se obtienen supuestas las corrientes de malla del circuito de la Figura 7.34, son las siguientes:
0 = I2 (1000 + 1000 + 1000) − 1000I1
(Malla de I2 )
Hemos obviado la ecuación de la malla de I1 , pues directamente sabemos que la corriente I1 es
nula, dado que coincide con la que circula por la rama en la que se encuentra el circuito abierto.
La ecuación de la malla de I2 , bajo la condición I1 = 0, se simplifica hasta obtenerse I2 = 0.
Ahora bien, según la Ley de Ohm, I2 , corriente que circula por la resistencia que hay entre los
terminales A y B, es:
I2 =
VA0 − VB0
VA0
VAB0
=
=
=0⇔
1000
1000
1000
VA0 = 0
Supongamos ahora que sólo actúa la fuente de corriente. Nos queda entonces el circuito de la
Figura 7.35, en el que se aprecia que la fuente de tensión ha sido sustituida por un cortocircuito.
La tensión VAB la obtendremos mediante el método de las mallas. Dado que hay un generador
de corriente, a éste se le debe asignar una polaridad ası́ como un valor de tensión (Vg ), que
será otra incógnita del sistema de ecuaciones a resolver. Suponiendo las corrientes de malla
asignadas en la Figura 7.35, las ecuaciones de malla que se obtienen son las siguientes:
Vg = I1 (1000 + 1000) − 1000I2
0 = I2 (1000 + 1000 + 1000) − 1000I2
Además, la fuente de corriente impone la ecuación:
I1 = 10 · 10−3
(Malla de I1 )
(Malla de I2 )
152
CAPÍTULO 7. TEOREMAS
1KΩ
1mA
1KΩ
A
+
Vg
1KΩ
I1
1KΩ
I2
B
Figura 7.35: obteniendo la tensión Thevènin
2000/3Ω
A
1/3V
B
Figura 7.36: equivalente Thevènin
Esto se debe a que la corriente de malla I1 coincide con la corriente que la fuente de corriente
impone en su rama. Tras resolver el sistema de ecuaciones se obtiene:
5
1
A, Vg = V
3000
3
Además, I2 se puede reescribir, según la Ley de Ohm, como:
I1 = 1 · 10−3 A, I2 =
VA1
1
VA1 − VB1
=
=
⇔
1000
1000
3000
1
VA1 = V
3
Para obtener la tensión total en el punto A, la cual coincide con la tensión Thevènin al haber
colocado la tierra en B, debemos sumar cada uno de los valores parciales obtenidos de tensión,
es decir:
1
1
Vt = VA0 + VA1 = 0 + = V
3
3
El equivalente Thevènin es por tanto el de la Figura 7.36. El equivalente Norton se puede obtener
directamente del Thevènin, aplicando las fórmulas de la equivalencia entre estos, estudiadas en
la sección 7.4. La relación entre el modelo Thevènin y el Norton para que estos sean equivalentes
está dada por las ecuaciones:
I2 =
Vt
Rt
Rn = Rt
In =
De las cuales se obtiene, trivialmente:
In =
1/3
= 5 · 10−4 A
2000/3
2000
Rn =
Ω
3
153
7.5. TEOREMAS, EJERCICIOS
A
5•10-4A
2000/3Ω
B
Figura 7.37: equivalente Norton
Teniéndose que el equivalente Norton buscado es el de la Figura 7.37.
Ejercicio 7.3: Determinar el equivalente Norton entre A y B del circuito de la Figura 7.38.
1KΩ
1KΩ
1mA
A
1KΩ
2V
1KΩ
1V
B
Figura 7.38: Ejemplo 7.3
Solución
Para obtener el equivalente Norton del circuito de la Figura 7.38 hallaremos tanto la resistencia Norton como la corriente Norton.
Pasemos pues a obtener la resistencia Norton, es decir, la resistencia medida entre los terminales A y B cuando se han anulado todas las fuentes internas. Si anulamos las fuentes internas
del circuito, obtenemos el conjunto de resistencias de la Figura 7.39. Asociando en serie el
circuito abierto con la resistencia de 1KΩ, obtenemos el conjunto de resistencias de la Figura
7.40.
Al asociar en paralelo la resistencia de 1KΩ con el circuito abierto, se obtiene el conjunto de
resistencias de la Figura 7.41. Obsérvese cómo, tal y como ya se ha comentado con anterioridad,
la rama donde se situa un circuito abierto puede ser directamente omitida a la hora de considerar
1KΩ
1KΩ
1KΩ
A
1KΩ
B
Figura 7.39: obteniendo la resistencia Norton
154
CAPÍTULO 7. TEOREMAS
1KΩ
A
1KΩ
1KΩ
B
Figura 7.40: obteniendo la resistencia Norton
1KΩ
A
1KΩ
1KΩ
B
Figura 7.41: obteniendo la resistencia Norton
el cálculo de la resistencia Norton. La resistencia equivalente que se obtiene del circuito de la
Figura 7.41 es trivial, y su valor es de:
Rn =
2000
Ω
3
La corriente Norton es la corriente que circula por el cortocircuito entre A y B, cuando dichos
terminales han sido cortocircuitados en el circuito original. La Figura 7.42 muestra el circuito
original en el que se han cortocircuitado los terminales A y B. En dicho circuito se han señalado
las corrientes que entran y salen del nudo C. Dado que los puntos A y B están cortocirucitados, la
resistencia de la corriente IC soporta una diferencia de tensión nula, y por ella no podrá circular
corriente, es decir, IC = 0. Deducimos pues que la rama de la corriente IC es superflua en lo
que al cálculo de la corriente Norton respecta. En la Figura 7.43 se muestra el circuito con
la rama de IC omitida para el cálculo de la corriente Norton. Las corrientes, además, se han
renombrado, junto con el nodo C, que no representa el mismo nodo C que el del circuito de la
Figura 7.42.
Resolvamos el circuito mediante el método de los nudos, para obtener I3 , que coincide con
1KΩ
1KΩ
C
A
Ia
1mA
2V
1KΩ
1V
Ib
Ic
1KΩ
B
Figura 7.42: hallando la corriente Norton
155
7.5. TEOREMAS, EJERCICIOS
1KΩ
I1
1mA
2V
1KΩ
C
I2
A
I3
1KΩ
1V
B
Figura 7.43: hallando la corriente Norton
A
1mA
2000/3Ω
B
Figura 7.44: equivalente Norton
la corriente de Norton buscada. Si aplicamos la ley de los nudos al nudo C, se tiene:
I1 = I2 + I3
Y sustituyendo las corrientes por sus respectivas expresiones (según la Ley de Ohm y según los
valores impuestos por las fuentes del circuito), obtenemos:
10 · 10−3 =
VC
VC − 1
+
1000
1000
De donde se deduce fácilmente que VC = 1, y la corriente I3 es:
I3 =
VC
1
=
= 1 · 10−3 A
1000
1000
Que coincide con la corriente Norton, como habı́amos dicho, es decir:
In = 1 · 10−3 A
El equivalente Norton que se obitiene es, por tanto, el de la Figura 7.44. Recuérdese que, dado
que la corriente Norton que se obtuvo del circuito original era la que circulaba de A a B,
entonces la fuente de corriente Norton ha de aparecer orientada, en el equivalente Norton, de
B a A, y su valor ha de ser justamente el de la corriente Norton hallada.
Ejercicio 7.4: Se pide obtener el valor de la tensión Vo en el circuito de la Figura 7.45. Se
recomienda, para su resolución, hallar el equivalente Thevènin desde el punto A hasta tierra, y
hacia la izquierda. Nótese que β = 200.
Solución
156
CAPÍTULO 7. TEOREMAS
10V
82KΩ
4KΩ
Vo
0,7V
βIB
A
IB
18KΩ
1KΩ
Figura 7.45: Ejemplo 7.4
Este circuito representa el modelo lineal de un transistor bipolar de unión npn en región
activa. Por ahora, esto nos importa bien poco: para nosotros, este circuito no es más que uno
más. En un futuro no muy lejano nos familiarizaremos con él, más a fondo.
Para resolver este circuito se nos sugiere que hagamos el Thevènin del subcircuito que
se ve desde el punto A hacia tierra, y hacia la izquierda. Para poder apreciar que en efecto
podemos obtener el Thevènin de esta parte del circuito, es conveniente redibujarlo. El cirucito
de la Figura 7.46 es equivalente al de la Figura 7.45, dado que en los dos puntos a los que se
suministraba una tensión de 10V (parte superior de las resistencias de 82KΩ y de 4KΩ) siguen
teniendo una tensión de 10V .
El Thevènin que se nos pide hacer para simplificar el circuito es el que marca la flecha que
se extiende desde el punto A al punto B, y hacia la izquierda.
La Figura 7.47 muestra el subcircuito del que se obtendrá el equivalente Thevènin.
La resistencia Thevènin es trivial, y su valor es igual al paralelo de las resistencias de 18KΩ
y 82KΩ:
Rt = 82000||18000 = 14760Ω
Además, la tensión Thevènin es la de un divisor de tensión:
18000
= 1,8V
Vt = VAB = 10 ·
18000 + 82000
Una vez sustituido en el circuito original el respetivo equivalente Thevènin, obtenemos un
circuito simplificado, como el de la Figura 7.48.
Resolvamos el circuito de la Figura 7.48 mediante el método de los nudos. Nótese que los
puntos marcados como A y B en el circuito de la Figura 7.48 no están relacionados con los
puntos A y B señalados en el circuito de la Figura 7.46.
De nudo E se deduce:
IB + IC = IE
Tengamos en cuenta que la corriente IC coincide con la corriente que la fuente dependiente de
corriente inyecta en su rama, y por ende:
IC = βIB
157
7.5. TEOREMAS, EJERCICIOS
10V
82KΩ
4KΩ
Vo
0,7V
10V
βIB
A
IB
18KΩ
1KΩ
B
Figura 7.46: circuito de la Figura 7.45, redibujado
82KΩ
10V
A
18KΩ
B
Figura 7.47: subcircuito del que obtener el Thevènin
10V
IC
A
14760Ω
4KΩ
Vo
0,7V
βIB
B
E
IB
1,8V
IE
1KΩ
Figura 7.48: circuito original, simplificado
158
CAPÍTULO 7. TEOREMAS
De donde:
IB + βIB = IE ⇔
(β + 1)IB = IE
Si ahora se sustituye cada corriente por la expresión que las define según la Ley de Ohm, se
obtiene:
VA − VB
VE
(β + 1)
=
14760
1000
Ahora bien, según la fuente de tensión de 1,8V , VA = 1,8; como además β = 200 y la fuente
de tensión de 0,7V implica que VB − VE = 0,7 ⇒ VE = VB − 0,7, si sustituimos todas estas
ecuaciones en la ecuación del nudo E, tenemos:
1,8 − VB
VB − 0,7
201
=
14760
1000
De donde se obtiene:
VB = 1,725V
Ası́,
1,8 − 1,725
= 5,098 · 10−6 A
14760
Y por tanto, como IC = βIB , se tiene:
IB =
IC = 200IB = 1,0196 · 10−3A
Pero además:
IC =
10 − Vo
= 1,0196 · 10−3 ⇔
4000
Vo = 5,921V
Ejercicio 7.5: Se pide calcular el equivalente Norton entre los terminales A y B del circuito
de la Figura 7.49, y a partir de él, el equivalente Thevènin.
1KΩ 10mA
1KΩ
10V
1KΩ
1KΩ
A
1KΩ
10V
1KΩ
10mA
B
Figura 7.49: Ejemplo 7.5
Solución
Para obtener el equivalente Norton, debemos obtener tanto la resistencia Norton como la
corriente Norton.
159
7.5. TEOREMAS, EJERCICIOS
(1)
(2)
1KΩ
1KΩ
1KΩ
1KΩ
A
1KΩ
1KΩ
B
Figura 7.50: obteniendo la resistencia Norton
1KΩ
1KΩ
A
1KΩ
B
Figura 7.51: obteniendo la resistencia Norton
La resistencia Norton es la resistencia equivalente que se mide entre los terminales A y B
cuando las fuentes internas del circuito han sido anuladas. La Figura 7.50 muestra el circuito
original con las fuentes anuladas.
En la Figura 7.50, el conjunto englobado en lineas discontinuas denominado (1) se reduce
a una resistencia de 1KΩ, ya que la rama que contiene el circuito abierto puede ser omitida
para el cálculo de la resistencia equivalente. A su vez, el conjunto denominado (2) se reduce a
un circuito abierto. Al final, la resistencia de 1KΩ que se obtiene del conjunto (1) es asociada
en serie con el circuito abierto que se obtiene del conjunto (2), quedando, en efecto, un circuito
abierto, y simplificándose el conjunto de resistencias al que se muestra en la Figura 7.51.
Del conjunto de resistencias de la Figura 7.51 se obtiene que la resistencia equivalente medida
entre A y B, que coincide con la resistencia Norton, es:
Rn =
2000
Ω
3
La corriente Norton es la corriente que circula por el cortocircuito que se crea entre los puntos
A y B. La Figura 7.52 muestra el circuito original con los terminales A y B cortocircuitados,
ası́ como la corriente In , corriente Norton, que debemos calcular.
Respecto a este circuito, es importante hacer hincapié en dos aspectos.
En primer lugar, la fuente de tensión con la resistencia en serie (señalada en (1)) puede ser
sustituida por una fuente de corriente con resistencia en paralelo (ver sección 7.4). El valor de
dicha fuente de tensión es igual a 10/1000A, que coincide con el cociente entre el valor de la
fuente de tensión y el de la resistencia en serie. La resistencia en paralelo es igual a la resistencia
que hay conectada en serie a la fuente de tensión.
Por otro lado, hemos de ver que, dado que los puntos A y B están cortocircuitados, la
corrienteque circula por la resistencia de 1KΩ que está englobada en (2) es nula (consecuencia
160
CAPÍTULO 7. TEOREMAS
(1)
(2)
1KΩ 10mA
1KΩ
1KΩ
A
C
1KΩ
10V
IR
1KΩ
1KΩ
10V
IN
10mA
D
B
Figura 7.52: obteniendo la corriente Norton
1KΩ 10mA
1KΩ
1KΩ
C
In
1KΩ
10V
0,01A
A
1KΩ
10mA
D
B
Figura 7.53: obteniendo la corriente Norton
directa de la Ley de Ohm). Por tanto, la rama de IR puede ser ignorada a la hora de resolver
el circuito.
Teniendo en cuenta estos dos aspectos, el circuito de la Figura 7.52 se reduce al circuito de
la Figura 7.53.
Se podrı́a pensar ahora que haciendo estos cambios no hemos llegado a ninguna parte, pero
lo cierto es que, a partir de aquı́, el cálculo de la corriente Norton es trivial.
Si asociamos en paralelo las dos resistencias que se encuentran conectadas a los puntos C y
D, obtendrı́amos una resistencia de 500Ω situada entre los puntos C y D. Ahora bien, en ese
caso, a partir del nudo C serı́a trivial obtener la corriente que circuları́a por dicha resistencia
de 500Ω, y por tanto se podrı́a obtener la diferencia de tensión VCD , en base a la cual se puede
obtener la corriente In .
La Figura 7.54 muestra el circuito en el que se han asociado las dos resistencias de 1KΩ, y
en el que se puede obtener, trivialmente, la tensión VCD mediante el empleo de la ecuación del
nudo C:
I1 + I2 = I3
Sustituyendo los valores de I1 e I2 por los valores que imponen las fuentes de corriente, y
sustituyendo I3 por su valor según la Ley de Ohm, se tiene:
10 · 10−3 + 0,01 =
VCD
500
De donde se obtiene:
VCD = 10V
Si ahora volvemos al circuito de la Figura 7.53, tenemos que la corriente Norton es:
In =
VCD
10
=
= 10 · 10−3 A
1000
1000
161
7.5. TEOREMAS, EJERCICIOS
1KΩ 10mA
1KΩ
1KΩ
10V
C
I1
0,01A
I2
I3
500Ω
10mA
D
Figura 7.54: obteniendo la corriente Norton
A
10mA
2000/3Ω
B
Figura 7.55: equivalente Norton buscado
Obsérvese que, dado que la corriente Norton hallada es la que circula de A a B en la Figura
7.52, la fuente de corriente Norton debe orientarse de B a A en el equivalente Norton. Se tiene
que, por tanto, el equivalente Norton buscado es el de la Figura 7.55
Para obtener el equivalente Thevènin asociado, basta aplicar la equivalencia estudiada en
la sección 7.4. La relación existente entre el equivalente Norton y el equivalente Thevènin de
un circuito es:
Rt = Rn
Vt = In Rn
De modo que la resistencia Thevènin es la misma que la resistencia Norton, y la tensión
Thevènin, la dada por:
2000
20
Vt = In Rn = 10 · 10−3 ·
= V
3
3
Y por tanto, el equivalente Thevènin buscado es el que se muestra en la Figura 7.56.
Ejercicio 7.6: Se pide determinar la corriente Io mediante el principio de superposición en el
circuito de la Figura 7.57.
2000/3Ω
A
20/3V
B
Figura 7.56: el equivalente Thevènin buscado
162
CAPÍTULO 7. TEOREMAS
1KΩ
1KΩ
1KΩ
1KΩ
10mA
Io
1KΩ
1KΩ
10V
Figura 7.57: Ejemplo 7.6
1KΩ
1KΩ
1KΩ
1KΩ
10mA 1KΩ
1KΩ
Figura 7.58: circuito original con la fuente de tensión anulada
Solución
Para resolver este circuito mediante el principio de superposición, supongamos primero que
sólo actúa la fuente de corriente (anulamos la fuente de tensión). El circuito que queda es el
que se muestra en la Figura 7.58.
En el circuito de la Figura 7.58 se ha señalado, mediante una flecha discontinua, un conjunto
de resistencias que pueden ser asociadas para simplificar en análisis del circuito. Recuérdese
que se está intentando obtener la corriente que circula por la resistencia de 1KΩ, vertical, que
se sitúa en la rama inmediatamente a la derecha de la fuente de corriente. Por tanto, todo lo
englobado por la flecha discontinua puede ser asociado para simplificar el análisis del circuito.
La resistencia equivalente del conjunto de resistencias englobado por la flecha es 5000/3Ω. Si
sustituimos dicho conjunto por su resistencia equivalente, obtenemos el circuito de la Figura
7.59.
Del circuito de la Figura 7.59 es trivial obtener la corriente Io1 , corriente que circula por
1KΩ
A
I1
10mA Io1
I2
1KΩ
5000/3Ω
Figura 7.59: obteniendo la corriente Io1
163
7.5. TEOREMAS, EJERCICIOS
1KΩ
1KΩ
1KΩ
1KΩ
1KΩ
1KΩ
10V
Figura 7.60: circuito original con la fuente de corriente anulada
1KΩ
1KΩ
I1
Io2
1KΩ
1KΩ
I2
10V
1KΩ
Figura 7.61: obteniendo la corriente Io2
la resistencia vertical de 1KΩ (obsérvese cómo se ha introducido una toma de tierra, cuya
utilidad, realmente, es nula: podrı́a haberse obtenido Io1 sin la necesidad de ella).
Aplicando el método de los nudos al nudo A del circuito de la Figura 7.59 se obtiene:
I1 = Io1 + I2
Si sustituimos cada corriente por su expresión por la Ley de Ohm, y en el caso de I1 , por el
valor que impone la fuente de corriente, se tiene:
10 · 10−3 =
VA
VA
+
1000 5000/3
De donde se obtiene:
VA = 6,25
Y por tanto:
VA
= 6,25 · 10−3
1000
Para seguir resolviendo el circuito mediante el principio de superposición, supongamos que,
ahora, sólo actúa la fuente de tensión (anulamos la fuente de corriente). El circuito que se
obtiene es el de la Figura 7.60.
En dicho circuito, una de las ramas contiene un circuito abierto, y por tanto por ella no
puede circular corriente, motivo por el cual puede ser omitida a la hora de resolver el circuito.
La Figura 7.61 muestra el circuito de la Figura 7.60, pero con esa rama omitida.
La corriente que pretendemos obtener es la corriente Io2 . Para resolver este circuito, usaremos
el método de las mallas. Las ecuaciones de mallas que se obtienen, definidas las corrientes de
malla de la Figura 7.61, son las siguientes:
Io1 =
10 = I1 (1000 + 1000 + 1000) − 1000I2
−10 = I2 (1000 + 1000 + 1000) − 1000I1
(Malla de I1 )
(Malla de I2 )
164
CAPÍTULO 7. TEOREMAS
De donde se obtiene:
I1 = 2,5 · 10−3 , I2 = −2,5 · 10−3
Como, además, I1 coincide con Io2 , tenemos:
Io2 = 2,5 · 10−3
La corriente Io original buscada, del circuito de la Figura 7.57, aplicando el principio de superposición, es la suma de las dos corrientes parciales Io1 e Io2 obtenidas, es decir:
Io = Io1 + Io2 = 2,5 · 10−3 + 6,25 · 10−3 = 8,75 · 10−3A
Ejercicio 7.7: Se pide determinar el equivalente Norton, entre los terminales A y B, del
circuito de la Figura 7.62.
1KΩ
1KΩ
A
10V
1KΩ
1KΩ
1KΩ
B
Figura 7.62: Ejemplo 7.7
Solución
Para obtener el equivalente Norton debemos obtener tanto la resistencia Norton como la
corriente Norton.
En primer lugar, obtengamos la resistencia Norton. La resistencia Norton es la resistencia
equivalente que se mide entre los terminales externos, A y B, cuando todas las fuentes internas han sido anuladas. Si anulamos todas las fuentes del circuito nos queda el conjunto de
resistencias de la Figura 7.63.
La resistencia equivalente del conjunto de resistencias de la Figura 7.63 es trivial, y su valor
es de 4000/7Ω, es decir:
4000
Ω
Rn =
7
1KΩ
1KΩ
1KΩ
1KΩ
A
1KΩ
B
Figura 7.63: obteniendo la resistencia Norton
165
7.5. TEOREMAS, EJERCICIOS
(1)
(2)
1KΩ
1KΩ
A
10V
1KΩ
1KΩ
In
1KΩ
B
Figura 7.64: obteniendo la corriente Norton
1KΩ
1KΩ
A
10V
In
500Ω
I1
I2
B
Figura 7.65: obteniendo la corriente Norton
El siguiente paso es obtener la corriente Norton. La corriente Norton es la corriente que circula
por el cortocircuito que se crea entre los terminales externos A y B del circuito original. La
Figura 7.64 muestra el circuito original en el cual se han cortocircuitado los terminales A y B.
Obsérvese que el conjunto de resistencias englobados en (1) están conectadas en paralelo,
ya que sus terminales externos son comunes; por tanto, las asociaremos. Además, la resistencia
englobada en (2) puede ser omitida, debido a que sus terminales externos A y B están cortocircuitados, y por tanto por ella no circula corriente. Si tenemos en cuenta estos dos detalles,
el circuito de la Figura 7.64 puede simplificarse, obteniendo el circuito de la Figura 7.65.
El circuito de la Figura 7.65 puede resolverse fácilmente mediante el método de las mallas.
Si consideramos las corrientes de malla definidas en la Figura 7.65, obtenemos las siguientes
ecuaciones de malla:
10 = I1 (1000 + 500) − 500I2
0 = I2 (1000 + 500) − 500I1
(Malla de I1 )
(Malla de I2 )
De estas ecuaciones de malla se obtiene:
I1 = 7,5 · 10−3, I2 = 2,5 · 10−3
Como, además, la corriente I2 coincide con la corriente In , se tiene que la corriente Norton es:
In = 2,5 · 10−3 A
El equivalente Norton buscado es, ası́ pues, el de la Figura 7.66.
Ejercicio 7.8: Determinar, mediante superposición, la potencia consumida o generada por la
fuente de corriente de valordel circuito de la Figura 7.67.
166
CAPÍTULO 7. TEOREMAS
A
2,5•10-3A
4000/7Ω
B
Figura 7.66: el equivalente Norton buscado
1KΩ
1KΩ
1KΩ
10V
1KΩ
Is=10mA
1KΩ
Figura 7.67: Ejemplo 7.8
Solución
Señalemos dos puntos de interés, A y B, y establezcamos una toma de tierra que nos ayude
en los cálculos necesarios (Figura 7.68). Recuérdese que, al pedirnos la potencia consumida o
generada por la fuente Is , necesitamos calcular la tensión que dicha fuente de corriente soporta.
Ésa será, de hecho, la incógnita que obtendremos mediante el principio de superposición. Fijados
A, B y la toma de tierra, es evidente que la tensión que soporta la fuente de corriente entre
su extremo superior y su extremo inferior coincide con la tensión en el punto A. Ası́ pues,
obtendremos, mediante superposición, la tensión en A. Recuérdese, además, que el principio de
superposición nos permite obtener tensiones o corrientes, pero no potencias, motivo por el cual
debemos obtener la tensión que soporta la fuente, más que obtener directamente su potencia.
Para resolver este circuito mediante el principio de superposición, supongamos que, en
primer lugar, actúa solamente la fuente de tensión de 10V , de modo que la fuente de corriente es anulada. Cuando la fuente de corriente es anulada, ésta es sustituida por un circuito
abierto, y por tanto la rama en la que se sitúa puede ser omitida para la resolución del circuito.
En la Figura 7.69 se muestra el circuito original con la fuente de corriente anulada. Este
circuito será resuelto mediante el método de las mallas. Las ecuaciones de malla que se obtienen,
1KΩ
1KΩ
A
1KΩ
B
10V
1KΩ
Is=10mA
1KΩ
Figura 7.68: Ejemplo 7.8, con algunos puntos de interés y toma de tierra marcados
167
7.5. TEOREMAS, EJERCICIOS
1KΩ
1KΩ
A
1KΩ
B
10V
1KΩ
I1
1KΩ
I2
Figura 7.69: circuito original con la fuente de corriente anulada
supuestas las corrientes de malla de la Figura 7.69, son las siguientes:
10 = I1 (1000 + 1000) − 1000I2
0 = I2 (1000 + 1000 + 1000 + 1000) − 1000I1
(Malla de I1 )
(Malla de I2 )
De donde se obtiene, directamente:
I1 =
1
1
, I2 =
175
700
Ahora bien, I2 , corriente que circula por la resistencia vertical de 1KΩ de la derecha, se puede
expresar según la Ley de Ohm, y obtener:
I2 =
VB
1
=
⇔
1000
700
10
VB =
7
Además, la corriente I2 también puede expresarse según la expresión que impone la resistencia
situada entre los puntos A y B, como:
VA0 − VB
⇔
1000
1
VA0 − 10/7
=
⇔
1000
700
20
VA0 = V
7
I2 =
Obsérvese que la tensión obtenida, VA0 , coincide con la tensión que soporta la fuente de corriente
entre su extremo superior y su extremo inferior, ya que la tensión en su extremo inferior es cero
por estar conectada a la toma de tierra.
Obtengamos ahora la tensión en el punto A cuando se anula la fuente de tensión. Si se anula
la fuente de tensión, obtenemos el circuito de la Figura 7.70.
Es posible llevar a cabo una serie de simplificaciones en este circuito, que nos ayuden en
la obtención de la tensión en A. Concretamente, las dos resistencias de 1KΩ de la izquierda
pueden asociarse en paralelo, mientras que las dos resistencias de 1KΩ de la derecha, pueden
asociarse en serie. El circuito resultante se muestra en la Figura 7.71.
El circuito de la Figura 7.71 se puede resolver fácilmente aplicando el método de los nudos
al nudo A. En dicho nudo, la ecuación que se obtiene es:
I1 = I2 + I3
168
CAPÍTULO 7. TEOREMAS
1KΩ
1KΩ
A
1KΩ
1KΩ
Is=10mA
B
1KΩ
Figura 7.70: circuito original con la fuente de tensión anulada
A
I2
1500Ω
I3
I1
Is=10mA
2000Ω
Figura 7.71: circuito de la Figura 7.70, simplificado
Si sustituimos cada corriente por la expresión que impone la Ley de Ohm o bien la fuente de
corriente, se tiene:
VA1
VA1
10 · 10−3 =
+
1500 2000
De donde:
60
VA1 =
7
La tensión total que se mide en el punto A, aplicando el principio de superposición, es la suma
de cada una de las tensiones parciales obtenidas en A, es decir:
VA = VA0 + VA1 =
20 60
80
+
= V
7
7
7
¿Cuál es la potencia generada o consumida por la fuente de corriente? Para contestar a esta
pregunta, aplicaremos la expresión general de potencia (ecuación (1.3)) a la fuente de corriente:
dado que la corriente que consideraremos para la fórmula de la potencia atraviesa a la fuente
hacia arriba (10 · 10−3 ), la tensión que se debe tener en cuenta en la fórmula es la tensión que
se mide entre el extremo inferior y el extremo superior de la fuente, es decir, −VA . La potencia,
por tanto, queda ası́:
80
4
−3
P = 10 · 10 · −
=− W
7
35
Como se trata de potencia negativa, se trata de potencia generada, es decir, potencia que la
fuente de corriente pierde para que pueda ser aprovechada por el resto del circuito.
Ejercicio 7.9: Determinar el equivalente Thevènin del circuito de la Figura 7.72, visto desde
los terminales A y B.
169
7.5. TEOREMAS, EJERCICIOS
1KΩ
10mA
1KΩ
1KΩ
1KΩ
1KΩ
A
1KΩ
B
Figura 7.72: Ejemplo 7.9
1KΩ
10mA
2KΩ
1KΩ
1KΩ
A
1KΩ
B
Figura 7.73: Ejemplo 7.9, con algunas resistencias asociadas
Solución
Antes de obtener el equivalente Thevènin, podemos asociar algunas resitencias para ası́ simplificar el análisis del circuito. Concretamente, las dos resistencias de 1KΩ que están conectadas
en serie pueden ser asociadas, obteniéndose ası́ el circuito de la Figura 7.73.
Pasemos ahora a obtener la resistencia Thevènin. La resistencia Thevènin es la resistencia
medida entre los terminales A y B, anuladas las fuentes internas. Anuladas la fuente de corriente,
obtenemos el conjunto de resistencias de la Figura 7.74. La resistencia equivalente medida entre
A y B en l circuito de la Figura 7.74 es trivial, y su valor es de 1750Ω, es decir:
Rt = 1750Ω
La tensión Thevènin es la tensión medida entre los terminales A y B en el circuito original.
Recuérdese que, como tensión Thevènin, se puede medir tanto la diferencia de tensión VAB como
VBA , siendo la única diferencia la orientación (en cuanto a polaridad) que tendrá la fuente de
tensión Thevènin en el equivalente; como de costumbre, nosotros mediremos la diferencia VAB .
La Figura 7.75 muestra el circuito original, en el cual se ha colocado una toma de tierra y en el
cual, además, se han definido una serie de corrientes para cada rama del circuito. Recuérdese
que por la rama de la resistencia de 1KΩ situada entre C y A no puede circular corriente, ya
que termina en circuito abierto. Si aplicamos el método de los nudos considerando los nudos D
1KΩ
2KΩ
1KΩ
1KΩ
A
1KΩ
B
Figura 7.74: obteniendo la resistencia Thevènin
170
CAPÍTULO 7. TEOREMAS
1KΩ
2KΩ
D
1KΩ
C
A
I1
10mA
I2
1KΩ
I3
1KΩ
B
Figura 7.75: obteniendo la tensión Thevènin
1750Ω
A
2,5V
B
Figura 7.76: equivalente Thevènin buscado
y C, obtenemos las siguientes ecuaciones:
I1 = I2 + I3
I3 = I3
(Nudo D)
(Nudo C)
Aunque la ecuación del nudo C pueda resultar un tanto evidente, lo que se pretende resaltar
es el hecho de que la corriente I3 puede escribirse de dos modos: como la corriente que entra al
nudo C, es decir, como la corriente que atraviesa la resistencia de 2KΩ, y como la corriente que
sale del nudo C, es decir, como la corriente que atraviesa la resistencia de 1KΩ situada entre
los puntos C y B.
Si ahora sustituimos cada corriente por su expresión según la Ley de Ohm, y tenemos en
cuenta la presencia de fuentes de corriente y de tensión, obtenemos:


−3
I
1 = 10 · 10









V
D




V − VC
V
I
=



10 · 10−3 = D + D

 2 1000
1000
2000
⇒
VD − VC
VD − VC
VC



I
=



3

=
2000 




2000
1000


V


C

 I3 =
1000
Sistema de dos ecuaciones con dos incógnitas del cual se obtiene:
VC = 2,5, VD = 7,5
Como, además, VC = VA al no circular corriente por la rama de la resistencia de 1KΩ que hay
entre los puntos C y A, se tiene que la tensión Thevènin es:
Vt = VAB = 2,5V
Y por tanto el equivalente Thevènin buscado es el de la Figura 7.76.
171
7.5. TEOREMAS, EJERCICIOS
Ejercicio 7.10: Se pide determinar el equivalente Thevènin, y a partir de él, el Norton, del
circuito de la Figura 7.77, medido desde los terminales A y B. Se recomienda, para obtener la
tensión Thevènin, aplicar el principio de superposición.
1KΩ
1KΩ
1KΩ
1KΩ
A
1KΩ
10mA
10mA
10V
1KΩ
1KΩ
B
Figura 7.77: Ejemplo 7.10
Solución
En primer lugar vamos a hallar la resistencia Thevènin. La resistencia Thevènin es la resistencia equivalente medida entre A y B cuando las fuentes internas han sido anuladas. Si
anulamos las fuentes de corriente y las fuentes de tensión, se obtiene el conjunto de resistencias
de la Figura 7.78.
La resistencia equivalente medida entre A y B en el conjunto de resistencias de la Figura
7.78 es trivial, y su valor es de 7000/11Ω, es decir, la resistencia Thevènin es:
Rt =
7000
Ω
11
Para obtener la tensión Thevènin, en efecto, vamos a aplicar el principio de superposición.
Supongamos que, en primer lugar, sólo actúa la fuente de tensión (anulamos las de corriente).
Se obtiene entonces un circuito como el de la Figura 7.79. En dicho circuito, además, se han
señalado las corrientes de malla que usaremos para resolver el circuito. Las ecuaciones de malla
que se obtienen son las siguientes:
10 = 4000I1 − 1000I2
0 = 3000I2 − 1000I1
De donde se obtiene:
I1 =
1KΩ
1KΩ
(Malla de I1 )
(Malla de I2 )
3
1
, I2 =
1100
1100
1KΩ
1KΩ
A
1KΩ
1KΩ
1KΩ
B
Figura 7.78: obteniendo la resistencia Thevènin
172
CAPÍTULO 7. TEOREMAS
1KΩ
1KΩ
1KΩ
A
1KΩ
1KΩ
10V
I1
1KΩ
I2
B
Figura 7.79: obteniendo la tensión Thevènin
1KΩ
1KΩ
C
I1
1KΩ
D
I3
1KΩ
E
I5
A
I7
1KΩ
I2
10mA
10mA
I4
I6
1KΩ
1KΩ
B
Figura 7.80: obteniendo la tensión Thevènin
Teniendo en cuenta la expresión de I2 según la Ley de Ohm, se deduce:
VA0
⇔
1000
10
= V
11
I2 =
VA0
Y como VB0 = 0, entonces:
VAB0 =
10
V
11
Supongamos que ahora sólo actúan las fuentes de corriente (anulamos la fuente de tensión). Se
obtiene entonces el circuito de la Figura 7.80.
Aplicando el método de los nudos al circuito de la Figura 7.80 se obtienen las siguientes
ecuaciones:
I1 = I2 + I3
I3 + I4 = I5
I5 = I6 + I7
I7 = I7
(Nudo C)
(Nudo D)
(Nudo E)
(Nudo A)
La ecuación del nudo A debe resultarnos familiar, pues esta situación ya la hemos tenido en
varias ocasiones a lo largo de este libro. Esta ecuación simplemente nos dice que la corriente
I7 puede escribirse de dos modos distintos: como corriente que entra al nudo A (corriente que
circula por la resistencia situada entre E y A), y como corriente que sale del nudo A (corriente
que circula por la resistencia situada entre A y B).
Si sustituimos cada corriente por la expresión que imponen tanto la Ley de Ohm como las
173
7.5. TEOREMAS, EJERCICIOS
7000/11Ω
A
40/11V
B
Figura 7.81: equivalente Thevènin buscado
fuente s de corriente, obtenemos:

I1 = 10 · 10−3




VC



I
=
2


1000



VC − VD



I3 =


1000−3



I
=
10
· 10
4


VD − VE
I5 =


1000


VE



I6 =


1000



VE − VA



I7 =


1000



VA

 I7 =
1000
Sistema del cual se obtiene:
VA1 =
























VC
VC − VD



10 · 10−3 =
+


1000
1000



VD − VE
V
−
V
C
D


+ 10 · 10−3 =
1000
1000
⇒
V
−
V
V
V
−
VA


D
E
E
E




=
+




1000
1000
1000






V
V
−
V
A
E
A




=



1000
1000









130
150
60
30
V, VC =
V, VD =
V, VE = V
11
11
11
11
Y por tanto:
30
V
11
Ya hemos obtenido los dos valores parciales de la diferencia de tensión VAB , tensión Thevènin.
Para obtener la tensión Thevènin real, basta aplicar el principio de superposición, y sumarlos,
obteniendo:
10 30
40
Vt = VAB = VAB0 + VAB1 =
+
= V
11 11
11
Ası́ pues, el equivalente Thevènin serı́a el de la Figura 7.81. El equivalente Norton se obtiene
directamente aplicando la relación existente entre los equivalentes Thevènin y Norton (sección
7.4). Se obtiene que Rn = Rt = 7000/11Ω y que In = Vt /Rt = (40/11)/(7000/11) = 1/175A,
obteniéndose ası́ el equivalente Norton de la Figura 7.82.
Uno podrı́a preguntarse por qué carajo se recomendó, en el enunciado del ejercicio, hacer uso
del principio de superposición para resolver el circuito, si está claro que no nos ha proporcionado
ningún beneficio. La intención, realmente, era la de incitar al lector a aplicar este principio.
Hay que coger práctica, nos resulte útil aplicarlo o no. Ale, a aguantarse.
VAB1 =
Ejercicio 7.11: Determinar el equivalente Thevènin del circuito de la Figura 7.83, medido
desde los terminales A y B.
174
CAPÍTULO 7. TEOREMAS
A
1/175A
7000/11Ω
B
Figura 7.82: equivalente Norton buscado
1KΩ
1KΩ
A
1KΩ
10V
1KΩ
1KΩ
10mA
B
Figura 7.83: Ejemplo 7.11
Solución
En primer lugar, obtengamos la resistencia Thevènin. La resistencia Thevènin es la resistencia que se mide entre los terminales A y B cuando se han anulado todas las fuentes internas.
Tras anular la fuente de tensión y la fuente de corriente, se obtiene el conjunto de resistencias
de la Figura 7.84.
La resistencia equivalente medida entre A y B del conjunto de la Figura 7.84 es trivial, y
su valor es de 400Ω. Por tanto:
Rt = 400Ω
La tensión Thevènin es la tensión medida entre A y B en el circuto original. Para simplificar
el análisis del circuito, vamos a asociar en paralelo las dos resistencias verticales de 1KΩ de
la derecha. Nótese que, al asociarlas, los puntos marcados como A y B siguen existiendo, y
por tanto la tensión VAB podrá medirse en el circuito simplificado. Además, al asociar estas
dos resistencias, habremos eliminado una malla del circuito, con lo cual el análisis se simplificará bastante. El circuito resultante es el mostrado en la Figura 7.85. Se han señalado, en
dicha figura, las corrientes en las ramas del circuito, para resolverlo por el método de los nudos.
1KΩ
1KΩ
A
1KΩ
1KΩ
1KΩ
B
Figura 7.84: obteniendo la resistencia Thevènin
175
7.5. TEOREMAS, EJERCICIOS
1KΩ
D
1KΩ
C
I1
A
I3
10V
I2
1KΩ
500Ω
10mA
B
Figura 7.85: obteniendo la tensión Thevènin
400Ω
A
4V
B
Figura 7.86: equivalente Thevènin buscado
Si se aplica el método de los nudos a los nudos C y A, se obtienen las siguientes ecuaciones:
I1 + I2 = I3
I3 = I3
(Nudo C)
(Nudo A)
La ecuación del nudo A nos indica que la corriente I3 puede expresarse de dos modos: como
corriente que atraviesa la resistencia de 1KΩ situada entre C y A (corriente que entra en A),
y como corriente que atraviesa la resistencia de 500Ω. Si sustituimos cada corriente por su
expresión impuesta por la Ley de Ohm, y tenemos en cuenta que VD = 10 según la fuente de
tensión, ası́ como que I2 = 10 · 10−3 debido a la fuente de corriente, se tiene:


10
−
V
C




I1 =





1000−3 




I2 = 10 · 10 


10 − VC
VC − VA



−3



+
10
·
10
=
⇔
VC − VA
1000
1000
⇒
I
=
3


1000 
 VC − VA = VA






VA


1000
500




I3 =




500


VA = −18
Sistema de ecuaciones del cual se deduce:
VA = 4V, VC = 12V
Y por tanto la tensión Thevènin, VAB , es:
Vt = VAB = 4V
Se tiene pues que el equivalente Thevènin buscado es el de la Figura 7.86.
176
CAPÍTULO 7. TEOREMAS
1KΩ
A
1KΩ
1KΩ
5V
1KΩ
1KΩ
1KΩ
B
Figura 7.87: Ejemplo 7.12
P
1KΩ
A
1KΩ
I2
5V
1KΩ
1KΩ
I3
I1
1KΩ
1KΩ
B
Figura 7.88: obteniendo la tensión Thevènin
Ejercicio 7.12: Se pide calcular el equivalente Thevènin, medido entre los terminales A y B,
del circuito de la Figura 7.87.
Solución
En este ejemplo vamos a comenzar obteniendo la tensión Thevènin, dado que su cálculo es
sensiblemente más sencillo que el de la resistencia Thevènin.
Supongamos la toma de tierra y corrientes de malla que se indican en el circuito de la Figura
7.88. Las ecuaciones de malla que se obtienen son las siguientes:
5 = 3000I1 − 1000I2 − 1000I3
0 = 3000I2 − 1000I1 − 1000I3
0 = 3000I3 − 1000I1 − 1000I2
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
Del cual se obtiene:
I1 = 2,5 · 10−3 , I2 = 1,25 · 10−3, I3 = 1,25 · 10−3
I1 puede ser escrita como corriente que atraviesa la resistencia situada justo encima de la fuente
de tensión según la Ley de Ohm:
VP − VA
I1 =
1000
Ahora bien, VP = 5 según la fuente de tensión, y por tanto:
5 − VA
⇔
1000
VA = 2,5
I1 = 2,5 · 10−3 =
177
7.5. TEOREMAS, EJERCICIOS
1KΩ
A
1KΩ
1KΩ
1KΩ
1KΩ
1KΩ
B
Figura 7.89: obteniendo la resistencia Thevènin
1KΩ
A
1KΩ
A
1KΩ
1KΩ
Req
1KΩ
1KΩ
B
B
Figura 7.90: obteniendo la resistencia Thevènin
Y por tanto, la tensión Thevènin es:
Vt = VAB = 2,5V
Más complicado es obtener la resistencia Thevènin. Tras anular las fuentes internas del circuito
(la fuente de tensión de 5V ), obtenemos el conjunto de resistencias que se muestra en la Figura
7.89.
El problema de este conjunto de resistencias es el hecho de que, por desgracia, no puede
simplificarse mediante convencionales asociaciones en serie o en paralelo. Se trata de un conjunto
de resistencias que, al igual que otros ya vistos a lo largo de este libro, requieren ser simplificados
mediante el procedimiento general que, en su dı́a, se explicó en la sección 4.1, y que ha sido
aplicado a varios ejercicios a lo largo de este libro.
Recuérdese que dos circuitos con dos terminales externos son equivalentes si muestran la
misma relación entre la tensión aplicada a sus dos terminales externos y las corrientes de entrada
y de salida.
Al buscar la resistencia equivalente del conjunto de resistencias de la Figura 7.89, se está intentando buscar una equivalencia como la de la Figura 7.90, en el sentido de que, ante una
determinada tensión aplicada a los terminales A y B, ambos circuitos produzcan la misma corriente de entrada o de salida (recuérdese que la corriente de entrada coincide con la de salida).
En suma, lo que se busca es que la relación existente entre la tensión en los terminales A y B
y la corriente de entrada o salida sea igual en ambos circuitos.
Para obtener el valor de Req que consigue que, en efecto, ambos circuitos sean equivalentes,
aplicaremos a ambos circuitos una misma tensión V entre los terminales A y B, e igualaremos las
expresiones de las corrientes de entrada (o de salida), para ası́ despejar el valor de la incógnita
Req .
La Figura 7.91 muestra el conjunto de resistencia original, al que se le ha aplicado una
178
CAPÍTULO 7. TEOREMAS
Iout1
1KΩ
1KΩ
I3
A
1KΩ
1KΩ
I1
I4
I2
1KΩ
+
− V
1KΩ
Iin1 B
Figura 7.91: obteniendo la resistencia Thevènin
tensión genérica V a sus terminales A y B, y del cual se piensa obtener la corriente de entrada
(o de salida) Iin1 (que es igual a Iout ). Para obtener el valor de Iin se va a aplicar el método
de las mallas. En este caso, objetivamente hablando, el ejercicio es algo engorroso, ya que se
obtiene un sistema de cuatro ecuaciones con cuatro incógnitas, a saber:
−V = 2000I1 − 1000I4 − 1000I3
0 = 3000I2 − 1000I4 − 1000I3
0 = 3000I3 − 1000I2 − 1000I1 − 1000I4
0 = 3000I4 − 1000I2 − 1000I3 − 1000I1
(Malla
(Malla
(Malla
(Malla
de
de
de
de
I1 )
I2 )
I3 )
I4 )
Sistema de ecuaciones del cual se obtiene:
V
V
3V
3V
I1 = −
,I2 = −
,I3 = −
,I4 = −
500
1000
2000
2000
La corriente I1 coincide con la corriente de entrada del circuito, y por tanto:
V
500
Centrémonos ahora en el circuito de la resistencia equivalente. Si a dicho circuito le aplicamos
una tensión genérica V , la corriente de entrada (o de salida) es trivial, y se obtiene directamente
aplicando la Ley de Ohm (Figura 7.92):
Iin1 = −
Iin2 =
−V
Req
Recuérdese que, para que ambos circuitos sean equivalentes, las expresiones que relacionan la
tensión aplicada y la corriente de entrada (o de salida), han de ser iguales. Por tanto, para que
ello sea cierto, deberá cumplirse que las corrientes de entrada de ambos circuitos sean iguales
para cualquier valor de tensión V , es decir:
Iin1 = Iin2 ⇔
−V
−V
=
⇔
500
Req
Req = 500Ω
Por tanto, la resistencia Thevènin, que es la resistencia equivalente medida entre los terminales
A y B, es:
Rt = 500Ω
Quedando el equivalente Thevènin buscado como se representa en la Figura 7.93.
179
7.5. TEOREMAS, EJERCICIOS
A
Iout2
+
− V
Req
Iin2
B
Figura 7.92: obteniendo la resistencia Thevènin
500Ω
A
2,5V
B
Figura 7.93: equivalente Thevènin buscado
Ejercicio 7.13: Determinar el equivalente Norton del circuito de la Figura 7.94, medido entre
los terminales J y F.
1KΩ
2KΩ
1KΩ
J
1KΩ
10V
20V
1KΩ
F
Figura 7.94: Ejemplo 7.13
Solución
En primer lugar hallemos la resistencia Norton. La resistencia Norton es la resistencia equivalente medida entre J y F cuando se han anulado todas las fuentes internas. Tras anular las
fuentes internas queda un circuito como el de la Figura 7.95.
La resistencia equivalente medida entre J y F de dicho circuito es trivial, y su valor es de
12000/7Ω. Por tanto:
12000
Rn =
Ω
7
La corriente Norton es la corriente que circula por el cortocircuito creado entre los terminales
externos (J y F) en el circuito original. Recuérdese que se pueden obtener dos corrientes Norton,
la que circula de J a F o la que circula de F a J; el hallar una u otra nos indicará hacia dónde
180
CAPÍTULO 7. TEOREMAS
1KΩ
2KΩ
1KΩ
J
1KΩ
1KΩ
F
Figura 7.95: obteniendo la resistencia Norton
1KΩ
2KΩ
1KΩ
J
1KΩ
10V
I1
In
1KΩ
20V
I2
I3
F
Figura 7.96: obteniendo la corriente Norton
deberá de orientarse la fuente de corriente Norton en el equivalente Norton. Hallemos la corriente
Norton como la que circula de J a F.
La Figura 7.96 muestra el circuito original en el que se han cortocircuitado los terminales
externos J y F. Además, en dicho circuito se han señalado las corrientes de malla que se usarán
para su resolución. También se ha detacado la corriente Norton In , la cual, obsérvese, coincide
con la corriente de malla I3 . Las ecuaciones de malla que se obtienen del circuito son las
siguientes:
−10 = 2000I1 − 1000I2
20 = 4000I2 − 1000I1 − 1000I3
0 = 2000I3 − 1000I2
(Malla de I1 )
(Malla de I2 )
(Malla de I3 )
De donde se obtiene:
I1 = −2,5 · 10−3 , I2 = 5 · 10−3 , I3 = 2,5 · 10−3
Como I3 coincide con la corriente Norton, entonces:
In = 2,5 · 10−3 A
De este modo se tiene que el equivalente Norton del circuito original es el de la Figura 7.97.
Obsérvese que, al haber calculado In como la corriente que circula de J a F, en el equivalente,
la fuente de corriente Norton debe estar orientada de F a J.
Ejercicio 7.14: Obtener el equivalente Thevènin del circuito de la Figura 7.98, medido desde
los terminales A y B.
181
7.5. TEOREMAS, EJERCICIOS
J
2,5mA
12000/7Ω
F
Figura 7.97: equivalente Norton buscado
1KΩ
A
5V
1KΩ
1KΩ
B
Figura 7.98: Ejemplo 7.14
Solución
Comencemos obteniendo la resistencia Thevènin. La resistencia Thevènin es la resistencia
medida entre los terminales externos, A y B, cuando se han anulado las fuentes internas. Si
anulamos la fuente de tensión, nos queda el conjunto de resistencias de la Figura 7.99.
La resistencia equivalente medida entre A y B en dicho circuito es trivial, y su valor es de
500Ω. Por tanto:
Rt = 500Ω
La tensión Thevènin es la tensión que se mide entre los terminales externos A y B en el circuito
original. La Figura 7.100 muestra el circuito original en el que se han señalado corrientes de
malla para su resolución mediante el método de las mallas.
Las ecuaciones de malla que se obtienen del circuito son:
5 = 1000I1 − 1000I2
0 = I2 (1000 + 1000 + 1000) − 1000I1
(Malla de I1 )
(Malla de I2 )
De donde se obtiene:
I1 = 7,5 · 10−3, I2 = 2,5 · 10−3
Como I2 puede reescribirse en función de la tensión VAB según la Ley de Ohm, podemos obtener
1KΩ
1KΩ
A
1KΩ
B
Figura 7.99: obteniendo la resistencia Thevènin
182
CAPÍTULO 7. TEOREMAS
1KΩ
A
5V
1KΩ
I1
1KΩ
I2
B
Figura 7.100: obteniendo la tensión Thevènin
500Ω
A
2,5V
B
Figura 7.101: equivalente Thevènin buscado
fácilmente el valor de la tensión Thevènin (VAB ):
I2 =
VAB
= 2,5 · 10−3 ⇔
1000
VAB = 2,5V
Por tanto, la tensión Thevènin es:
Vt = VAB = 2,5V
Y el equivalente Thevènin el de la Figura 7.101.
Índice alfabético
Asociaciones
concepto, 31
en paralelo, 45
de bobinas, 48
de condensadores, 51
de corriente, 54
de resistencias, 46
de tensión, 53
en serie, 34
de bobinas, 35
de condensadores, 39
de fuentes de corriente, 44
de fuentes de tensión, 40
pérdida de información, 58
Bobina, 11
Circuito, 21
Condensador, 13
Corriente, 3
continua, 1
Diferencia de potencial, 1
Divisor de tensión, 124
Energı́a, 3
principio de conservación de la, 19
Entrada de un circuito, 119
Equivalencia
fuentes de corriente, 56
fuentes de tensión, 43
Fuente de
corriente, 18
tensión, 15
Linealidad, 127
Método de las mallas, 94
Método de los nudos, 62
Malla, 23
Nodo, 21
Norton
relación con Thevènin, 143
teorema de, 141
Nudo, 21
principal, 21
Operador lineal, 127
Potencia, 3
Principio de superposición, 127
Rama, 22
Resistencia, 9
Salida de un circuito, 119
Superposición
principio de, 127
Tensión, 1
Teorema
de Norton, 141
de Thevènin, 136
Thevènin
relación con Norton, 143
teorema de, 136
Toma de tierra, 2
Kirchhoff
ley de las mallas de, 27
ley de los nudos de, 24
leyes de, 21
Ley de las mallas, 27
Ley de los nudos, 24
Ley de Ohm, 7
Leyes de Kirchhoff, 21
183
184
ÍNDICE ALFABÉTICO
Bibliografı́a
[1] Juan A. López Villanueva, Juan A. Jiménez Tejada, Fundamentos de teorı́a de circuitos
para electrónica, Departamento de Electrónica y Tecnologı́a de Computadores, Universidad
de Granada, Granada, España.
[2] Juan A. López Villanueva, Juan A. Jiménez Tejada, Problemas de electrónica básica,
Departamento de Electrónica y Tecnologı́a de Computadores, Universidad de Granada,
Granada, España.
[3] Emilio Soria Olivas, Teorı́a de circuitos, Serie Schaum.
[4] Luis Prat Viñas, Fundamentos de electrónica - Circuitos y dispositivos electrónicos, Ediciones UPC.
185