CIRCUITOS MULTIFRECUENCIA Cuando aplicamos a un circuito

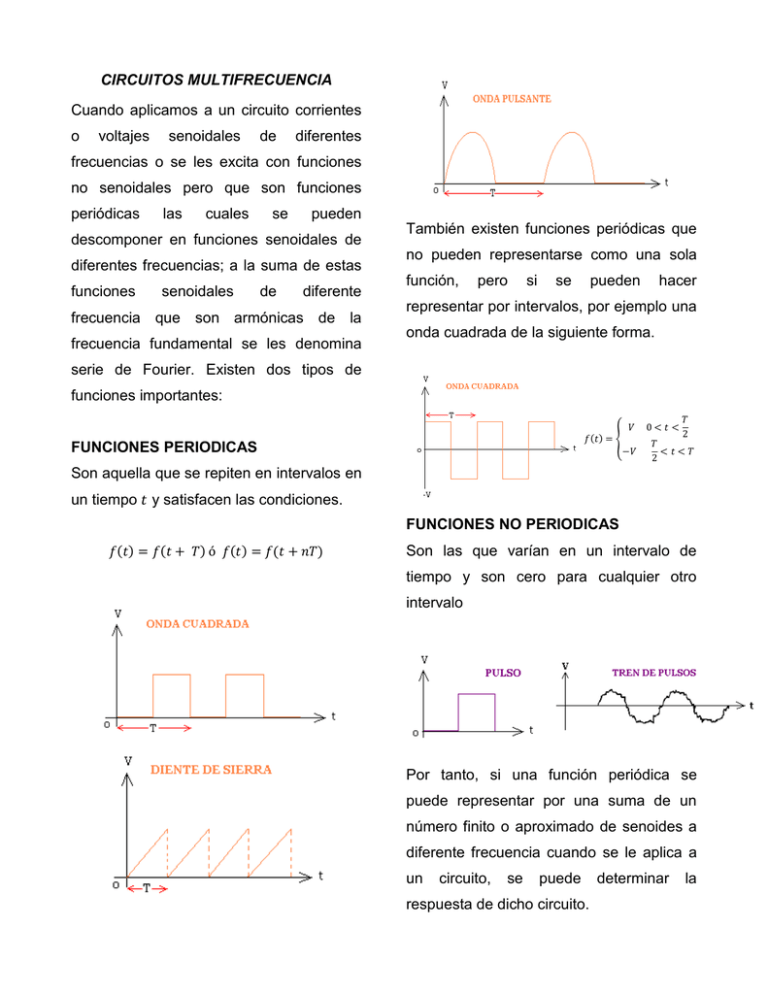
CIRCUITOS MULTIFRECUENCIA
Cuando aplicamos a un circuito corrientes
o
voltajes
senoidales
de
diferentes
frecuencias o se les excita con funciones
no senoidales pero que son funciones
periódicas
las
cuales
se
pueden
descomponer en funciones senoidales de
diferentes frecuencias; a la suma de estas
funciones
senoidales
de
diferente
frecuencia que son armónicas de la
frecuencia fundamental se les denomina
También existen funciones periódicas que
no pueden representarse como una sola
función,
pero
si
se
pueden
hacer
representar por intervalos, por ejemplo una
onda cuadrada de la siguiente forma.
serie de Fourier. Existen dos tipos de
funciones importantes:
FUNCIONES PERIODICAS
Son aquella que se repiten en intervalos en
un tiempo y satisfacen las condiciones.
FUNCIONES NO PERIODICAS
Son las que varían en un intervalo de
tiempo y son cero para cualquier otro
intervalo
Por tanto, si una función periódica se
puede representar por una suma de un
número finito o aproximado de senoides a
diferente frecuencia cuando se le aplica a
un
circuito,
se
puede
respuesta de dicho circuito.
determinar
la
Para
que
dicha
función
se
pueda
representar en la forma propuesta es
necesario que cumpla con las condiciones
de Dirichlet que son:
1. Que la función tenga un valor medio
finito en un período de tiempo
.
2. Que la función tenga un número finito
de máximos positivos y negativos en un
Cuando la función es par
impar
.
y si la función es
período de tiempo t.
3. Que
la
función
en
caso
de
ser
VALOR EFICAZ Y POTENCIA
discontinua tenga un número finito de
discontinuidades en un período de
Para una señal no senoidal pero que es
tiempo .
periódica el valor eficaz de la ecuación 3
será:
La serie de Fourie es la suma de senoides
de deferente frecuencia.
Para una función senoidal:
Cada una de las frecuencias de las
El valor de cada uno de los términos de la
serie de Fourier será:
senoides
frecuencia
fundamental
, se dice que es la
enésima
de
la
frecuencia
. Por tanto una función
periódica será descrita en términos de su
Para un circuito lineal con una tensión
frecuencia fundamental de su segunda
aplicada pueden considerarse
armónica de su tercera y de cada una de
corriente tenga las mismas armónicas que
esas frecuencias
la tensión aplicada pero con amplitud
período.
relacionadas con
el
diferentes si al voltaje aplicado es:
que la
La corriente sería:
1. RED AUXILIAR
DIRECTA
DE
CORRIENTE
En la cual se considera los términos
Los valores eficaces correspondientes:
constantes de las fuentes, sus ecuaciones
son:
De donde se obtienen la respuesta
de cada elemento.
2. RED AUXILIAR
ALTERNA
DE
CORRIENTE
En la cual se consideran las fuentes de
una frecuencia genérica numérica. Sus
ecuaciones son:
En la cual la
La potencia media es igual a:
Ó bien:
En el estado permanente si es excitado por
fuente del tipo:
Para analizarlo se descompone en 2 redes
auxiliares.