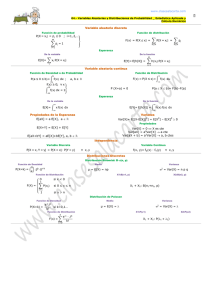
impulso-respuesta

Curso Combinado de Predicción y Simulación
www.uam.es/predysim
Edición 2004
UNIDAD 5: TÉCNICAS AVANZADAS DE PREDICCIÓN
Función de impulso-respuesta y análisis de descomposición de la varianza
La función de impulso-respuesta y el análisis de descomposición de la varianza analizan
las interacciones dinámicas que caracterizan al sistema estimado. Ello permite
identificarlas con la simulación del modelo. Con la simulación pretendemos analizar los
efectos que en las variables endógenas provocan variaciones de las variables exógenas.
Puesto que en los modelos VAR no existen estrictamente hablando variables exógenas, las
alteraciones se incluyen en algunas de las variables explicadas.
La función impulso-respuesta muestra la reacción (respuesta) de las variables explicadas
en el sistema ante cambios en los errores. Un cambio (shock) en una variable en el período
i afectará directamente a la propia variable y se transmitirá al resto de variables explicadas
a través de la estructura dinámica que representa el modelo VAR. Pongamos un ejemplo:
Supongamos que las exportaciones totales de bienes y servicios (EXGS) y las
importaciones totales de bienes y servicios (IMGS) están determinadas conjuntamente
por un modelo VAR de dos ecuaciones sin término independiente y con un retardo de
las variables endógenas. El modelo VAR resultante sería:
EXGS t = α 11 EXGS t −1 + α 12 IMGS t −1 + ε 1,t
IMGS t = β 11 IMGS t −1 + β 12 EXGS t −1 2 + ε 2,t
Un cambio en ε 1,t modificará inmediatamente el valor presente de EXGS, pero también
puede modificar los valores futuros de EXGS e IMGS al incluirse el valor retardado de
EXGS en ambas ecuaciones.
Si, en este ejemplo, las innovaciones ε 1,t y ε 2,t no están correlacionadas, la interpretación es
sencilla, pues ε 1,t sería la innovación para EXGS y ε 2,t la innovación para IMGS. La función
de respuesta de impulso para ε 2,t mide el efecto de una variación en los errores sobre los
valores actuales y futuros de las importaciones y el valor futuro de las exportaciones.
Sin embargo, normalmente los vectores de innovaciones están correlacionados, de forma
que presentan un componente común que no puede ser asociado a ninguna variable
Página 1 de 1
específica. Un procedimiento arbitrario, pero de uso generalizado, para resolver este
problema consiste en atribuir todo el efecto de cualquier componente común a la variable
que se especifica en primer lugar en el modelo VAR. En nuestro ejemplo, el componente
común de ε 1,t y ε 2,t se atribuye totalmente a ε 1,t , porque ε 1,t precede a ε 2,t . De esta forma,
ε 1,t es la innovación de las exportaciones, y ε 2,t , las innovaciones de las importaciones, se
transforman para sustraerles el componente común.
Técnicamente, esto significa que los errores se ortogonalizan por el procedimiento de
descomposición de Cholesky, de forma que la matriz de covarianzas de las innovaciones
resultante es diagonal. Aunque la descomposición de Cholesky es un método de uso
generalizado, no deja de ser bastante arbitrario a la hora de atribuir los efectos comunes.
Además, hay que tener siempre presente que al cambiar el orden de las ecuaciones, los
resultados de las funciones de repuesta de impulso pueden variar drásticamente.
En definitiva, las simulaciones con modelos VAR son atemporales, en el sentido de que
sólo recogen la influencia de acuerdo con el transcurso del tiempo, pero no están
asociadas a un período concreto, como en el caso de las simulaciones con modelos
estructurales. Operativamente la realización de simulaciones con modelos VAR se
realiza mediante los siguientes pasos:
1) Se ordenan las variables de mayor a menor exogeneidad relativa, lo cual conlleva
cierta carga de subjetividad, quizás análoga a la distinción entre variables endógenas y
predeterminadas que realizaos en los modelos estructurales.
2) Se transforma el modelo de acuerdo con una matriz deducida de la ordenación
realizada.
3) Se reestima el modelo transformado en su forma autorregresiva.
4) Se computa la representación de medias móviles del nuevo modelo estimado.
5) Se incorpora un determinado valor a la perturbación aleatoria de una ecuación,
normalmente equivalente a una desviación típica de dicha perturbación.
6) Se calculan los valores restantes de la transformación de dicha perturbación mediante la
matriz de medias móviles estimada en la fase 4.
7) Se representan los valores obtenidos para cada variable incluida en el sistema.
Dada la complejidad del proceso todos los programas que incluyen estimación de modelos
VAR tiene incorporadas rutinas para la obtención de estas funciones impulso-respuesta de
forma automática, tal y como veremos en el ejercicio 1.
Página 2 de 2
Otro método adicional para describir la dinámica del sistema de ecuaciones del modelo
VAR es el análisis de la descomposición de la varianza del error. La descomposición de
la varianza consiste en obtener distintos componentes que permitan aislar el porcentaje de
variabilidad de cada variable que es explicado por la perturbación de cada ecuación,
pudiéndose interpretar como la dependencia relativa que tiene cada variable sobre el resto.
Esta descomposición se obtiene con relativa facilidad en el caso en que los componentes
del vector de perturbaciones sean ortogonales.
Mientras que la función de respuesta de impulsos muestra el efecto de un cambio
(shock) en una de las variables endógenas sobre las demás variables del modelo VAR,
la descomposición de la varianza proporciona información acerca de la importancia
relativa de cada innovación aleatoria de las variables en el modelo VAR.
Además, si una proporción importante de la varianza de una variable viene explicada
por las aportaciones de sus propias perturbaciones, dicha variable será relativamente
más exógena que otras, de forma que este análisis de la varianza puede ayudarnos a
confirmar que el orden de “exogeneidad” que hemos introducido para la
ortogonalización de las perturbaciones aleatorias es correcto.
Página 3 de 3