68. Una línea de longitud l y orientada a lo largo del eje x, como en

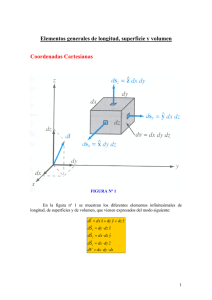
68. Una línea de longitud l y orientada a lo largo del eje x, como en la figura, tiene una
carga por unidad de longitud λ , la cual varia con x como λ=λo (x-d)/d, donde d es la
distancia de la línea del origen (punto P en la figura) y λ o es una constante. Encuentre el
campo eléctrico en el origen.
y
E
P
x
x
x
d
l
Solución:
Teniendo en cuenta que es una unidad infinitesimal de carga la
diferencial del campo eléctrico es igual a:
E = k * q = k * (λo * (x-d)/d) * x
x2
x2
Derivando
l+d
∫ ((x-d)/x2 *d) dx
E = k * λo
d
l+d
l+d
E = k * λo  ∫ (x/x2 *d) dx - ∫ (d/x2 *d) dx 
d
d
l+d
l+d
E = k * λo  1/d (ln x ) + (1/x ) 
d
d
E = k * λo  (1/d *(ln (l+d) - ln d)) + ((1/l+d)-(1/d))
E = k * λo  (1/d *(ln (l+d)/d) + (1/l+d)-(1/d)