Binomio de Newton - Colegio Ntra. Sra. del Pilar
Anuncio

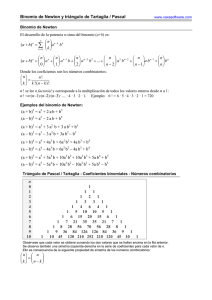
NÚMEROS COMBINATORIOS & EL BINOMIO DE NEWTON El símbolo MAT4-B , donde m y n son números naturales (enteros positivos) con n≤m, se define de la siguiente forma: Estos números combinatorios se llaman también coeficientes del binomio, por el binomio de Newton, que veremos más abajo. Sus propiedades son: ejemplo → Date cuenta que tiene exactamente n factores tanto en el numerador como en el denominador; y que es mejor calcular que porque es más sencillo. BINOMIO DE NEWTON A partir del Triángulo de Pascal o de Tartaglia (tiene los dos nombres) podemos desarrollar: n En el desarrollo de (a+b) pueden observarse las siguientes 5 propiedades: 1. Hay n+1 términos 2. La suma de los exponentes de a y de b en cada término es n 3. Los exponentes de a decrecen 1 unidad en cada término desde n hasta 0; los exponentes de b crecen similarmente de 0 a n 4. El coeficiente de cualquier término es donde k es el exponente de a o de b 5. Los coeficientes de términos equidistantes de los extremos son iguales Dpto. de Matemáticas colegio NUESTRA SRA DEL PILAR - Madrid