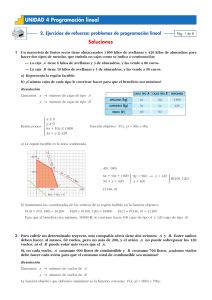
Ejercicio 4: Un comerciante quiere dar salida a 400 kg de avellanas
Anuncio

Ejercicio 4: Un comerciante quiere dar salida a 400 kg de avellanas, 300 kg de nueces y 4oo kg de almendras. Para ello hace dos tipos de lotes: los de tipo A contienen 2 kg de avellanas, 2 kg de nueces y 1 kg de almendras; y los de tipo B contienen 3 kg de avellanas, 1 kg de nueces y 4 kg de almendras. El precio de venta de cada lote es de 20 euros para los del tipo A y de 40 euros para los del tipo B. ¿Cuántos lotes de cada tipo debe vender para obtener el máximo ingreso y a cuánto asciende éste? Planteemos el problema: x=lotes de tipo A y=lotes de tipo B B(x,y)=20x+40y, será la función beneficio. Las restricciones son: x0 y 0 2x3x400 2x y300 x4y400 Punto Coordenada X Coordenada Y 0 Valor F O 0 0 A 0 B 0 300 12000 C 0 100 4000 D 200 0 4000 E 150 0 3000 F 400 0 8000 133.333333333 5333.33333333 G 125 50 4500 H 80 80 4800 I 114.285714286 71.4285714286 5142.85714286 Debe vender 80 lotes de cada tipo y obtendrá un beneficio de 4800 euros.