Teorema de Bayes El teorema de Bayes nos permite pasar de la

Teorema de Bayes
El teorema de Bayes nos permite pasar de la probabilidad a
priori a la probabilidad a posteriori (a la luz de los datos):
p(H | D) =
p(D | H)p(H)
p(D)
Si solo existen dos hipótesis, se ve claro que con los numeradores
nos basta para elegir la más probable:
p(D | H )p(H )
p(H1 | D) =
1
1
p(D)
p(D | H 2 )p(H 2 )
p(H 2 | D) =
p(D)
Como el denominador es un factor de normalización que no
depende de la hipótesis, podemos resumir esta fórmula como:
prob. a posteriori = verosimilitud x prob. a priori
Es decir, la verosimilitud nos permite refinar nuestro grado de
confianza en una hipótesis a la luz de los datos.
Dos formas de tomar decisiones
Lo correcto es quedarnos con la hipótesis que maximiza la
probabilidad a posteriori:
H i = max i p (H i | D)
Sin embargo, en ocasiones escogemos la hipótesis que maximiza
la verosimilitud pues es más sencillo como veremos en el futuro:
H i = max i p (D | H i )
Hemos tenido ocasión de comprobar que existen problemas, como
el del taxi, en los que las decisiones son opuestas siguiendo uno
y otro método.
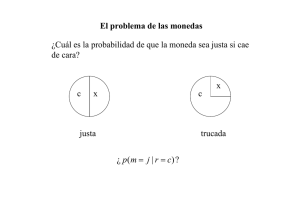
El problema de las monedas
En un saco tenemos monedas justas y trucadas. Las trucadas
caen tres de cada cuatro veces de cara. ¿Cuál es la probabilidad
de que una moneda sacada al azar sea justa si cae de cara?
x
c
x
c
justa
trucada
¿ p (m = j | r = c) ?
El problema de las monedas
p(m = j | r = c) =
p (r = c | m = j ) p (m = j ) 0.5 × 0.5 0.25
=
=
= 0.4
p (r = c)
p (r = c) 0.625
p(m = t | r = c) =
p ( r = c | m = t ) p (m = t ) 0.75 × 0.5 0.375
=
=
= 0.6
p(r = c)
p ( r = c) 0.625
p(r = c) = p(r = c | m = j ) p(m = j ) + p (r = c | m = t ) p(m = t )
p(r = c) = 0.5 × 0.5 + 0.75 × 0.5 = 0.625
Existe un 40% de probabilidad de que la moneda sea justa
si cae de cara.
El problema de las monedas
p(m = j | r = c) =
p (r = c | m = j ) p(m = j ) 0.5 × 0.5 0.25
=
=
= 0.4
p (r = c)
p(r = c) 0.625
p(m = t | r = c) =
p(r = c | m = t ) p (m = t ) 0.75 × 0.5 0.375
=
=
= 0.6
p(r = c)
p(r = c) 0.625
p(m = j | r = x) =
p(r = x | m = j ) p(m = j ) 0.5 × 0.5 0.25
=
=
= 0.67
p(r = x)
p (r = x) 0.375
p(m = t | r = x) =
p(r = x | m = t ) p(m = t ) 0.25 × 0.5 0.125
=
=
= 0.33
p(r = x)
p(r = x) 0.375
Cuatro clasificadores
Existen cuatro clasificadores para el problema de las monedas,
es decir, cuatro funciones del espacio de atributos en el de clases:
r ∈ {c, x} → m ∈{ j , t}
Modelo A
y (c ) = t
Modelo B
y ( x) = j
Modelo C
y (c ) = j
y ( x) = j
y (c ) = j
y ( x) = t
Modelo D
y (c ) = t
y ( x) = t
Probabilidad de equivocarse
Modelo A
y (c ) = t
y ( x) = j
El modelo A responde trucada cuando sale cara y justa cuando
sale cruz. Por lo tanto, la probabilidad de equivocarse es la
probabilidad de que: una moneda justa caiga de cara o una
moneda trucada caiga de cruz:
p(error ) = p(m = j , r = c) + p(m = t , r = x)
p(error ) = p(m = j | r = c) p(r = c) + p(m = t | r = x) p(r = x)
p(error ) = 0.4 × 0.625 + 0.33 × 0.375 = 0.37
Probabilidad de equivocarse
Modelo B
y (c ) = j
y ( x) = t
p(error ) = p(m = t , r = c) + p(m = j , r = x)
p(error ) = p(m = t | r = c) p(r = c) + p(m = j | r = x) p(r = x)
p (error ) = 0.6 × 0.625 + 0.67 × 0.375 = 0.63
Probabilidad de equivocarse
Modelo C
y (c ) = j
y ( x) = j
p (error ) = p (m = t , r = c) + p(m = t , r = x)
p (error ) = p (m = t | r = c) p(r = c) + p(m = t | r = x) p (r = x)
p (error ) = 0.6 × 0.625 + 0.33 × 0.375 = 0.5
Probabilidad de equivocarse
Modelo D
y (c ) = t
y ( x) = t
p (error ) = p (m = j , r = c) + p (m = j , r = x)
p(error ) = p(m = j | r = c) p(r = c) + p(m = j | r = x) p(r = x)
p(error ) = 0.4 × 0.625 + 0.67 × 0.375 = 0.5
Porcentaje de error de cada modelo
A
y (c ) = t
y ( x) = j
B
63 %
13
50 %
10
50 %
10
y (c ) = j
y ( x) = j
D
7
y (c ) = j
y ( x) = t
C
37 %
y (c ) = t
y ( x) = t
El mejor modelo (A)
es el que clasifica
cada ejemplo en la
clase con mayor
probabilidad a
posteriori.