dx P P x L e Determinar el desplazamiento relativo entre las dos

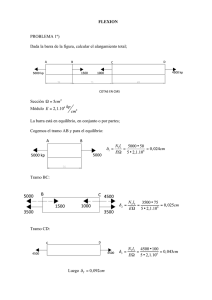
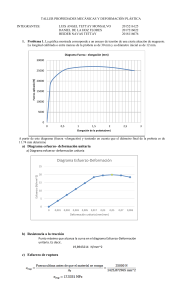
Ejercicio 3.1
Determinar el desplazamiento relativo entre las dos secciones
extremas de la barra de la figura:
e
P
b1
dx
P
b2
x
L
Datos:
e = 1 cm, b1= 5 cm, b2= 10 cm, L = 40 cm
P = 50.000 N, E = 2x107 N/cm2
, a una distancia x de la
Consideremos una rebanada de longitud 1dx
sección b1. El canto será:
−
b
2 b1
= b1 +
x = b1 + ax
L
a=
b2 − b1
L
El área (Ax) de la sección escogida será: (b1+a.x)e
Si esta rebanada experimenta una elongación du, su deformación será:
du
P
=
dx E ⋅ Ax
La elongación total, u, que experimenta la barra será:
∫
∫
P
dx
0
0
( b1 + ax ) e E
L
P L dx
P
=
u=
ln b1 + ax
P
P
b +0
a⋅L
e E 0 b1 + ax u = ∫ aeE
du = ∫
dx =
ln
E⋅A
a ⋅e⋅ E
b
+
P
b1 a L
=
ln
u
a eE
b1
u=
L
P
Ax E
∫
dx =
L
L
L
0
0
1
x
1
Sustituyendo
Substituting
backelforvalor
K,
u=
P
b 2 − b1
(
)eE
L
de a:
b2
ln
b1
En el problema: e = 1 cm, b 1= 5 cm, b2= 10 cm, L = 40 cm,
P = 50.000 N, E = 2 x 107 N/cm 2
u=
50.000
10− 5
7
(
) . 1 . 2. 10
40
ln
10
= 0,01386 cm
5