Ax=b ( )=

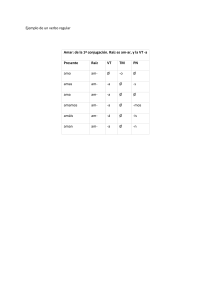
1.2 Representación matricial de un sistema mxn
1.3 Sistemas de resolución sencilla.
(
a11 x1 +a12 x2 +!+a1n xn =b1
Sistema triangular superior: U b*
a21 x1 +a22 x2 +!+a2n xn =b2
"
am1 x1 +am2 x2 +!+amn xn =bm
! a11
# a21
#
# !
#" a
m1
a12
a22
!
am2
… a1n $ ! x1 $ ! b1 $
… a2n & # x2 & # b2 &
&# & =# &
" ! & #! & #! &
… amn &% #" xn &% #" bm &%
(U
b
*
)
" 2
$
= $0
$
$# 0
!1
2
1
0
0
3
1 %
'
2 '
'
!1'&
1
5
x3 = ! !!!!!x2 = 2 !!!!!x1 = !
3
3
Sistema escalonado superior:
Ax=b
(M
b*
)
" 1
$
= $0
$
$# 0
2 !1
0
0
1
1
0 0
1
)
1 %
'
2 '
'
!1'&
(M
b*
)
x4 = !1 (v. pri.); x3 = 3
(v. pri.)
x2 = t (par.); !!x1 = 4 ! 2t (v. pri.)
1
! Resolución general de un sistema escalonado Mx = b*
Matriz ampliada
Ax=b
•
•
•
•
! a11
#a
( A b ) = # !21
#
#" a
m1
a12
a22
!
am2
3
… a1n
… a2n
" !
… amn
b1 $
b2 &
&
! &
bm &%
*
1. Si existe, en ( M b ) una fila ( 0,0,…,0!|!bk* ) con bk* ! 0 , entonces el
S.E.L. es incompatible, en caso contrario, el S.E.L. será compatible.
2. Si el sistema es compatible, entonces el conjunto solución se obtiene:
•
Solución
Se despejan las variables principales respecto al resto de
variables (llamadas no principales o parámetros);
Conjunto solución
•
Sistemas compatibles e incompatibles
Se asignan valores arbitrarios (s,t,.…) a las variables no
principales (parámetros) obteniéndose el conjunto solución.
Sistemas equivalentes:
dos sistemas son equivalentes si tienen el mismo conjunto solución
2
4
Sistemas lineales nxn
2. Método de Gauss y sus variantes.
• ¿cómo se puede conseguir un sistema equivalente al inicial
1." Eliminación o reducción de la matriz (A | b) a la forma (U | b* )
que esté en forma triangular superior? mediante las operaciones sobre las filas de ( A
b) :
mediante operaciones elementales sobre sus filas:
• Multiplicación por factores no nulos;
a) Multiplicación por factores no nulos (#Fi !Fi);
• Intercambio de filas;
b) Intercambio de filas (notación: Fi " Fj);
c) Sumar a una fila dada un múltiplo de otra (Fj+#Fi !Fj).
• Sumar a una fila dada un múltiplo de otra.
• ¿cuándo tiene solución? rango ( A b ) = rango ( A )
*
2." Resolución del sistema triangular, Ux = b , equivalente al inicial.
• ¿cuándo tiene solución única?
rango ( A ) = n
det ( A ) ! 0
!!A -1
5
7
Partimos de la matriz ampliada:
Si admite solución única, ¿cómo calcularla?
• métodos directos (solución exacta): Cramer, Gauss,
descomposición LU, etc..
(A
Obtienen la solución exacta tras un número finito de
operaciones
• métodos iterativos (aproximación a la solución exacta):
Jacobi, Gauss-Seidel, etc..
obtienen aproximaciones sucesivas con el objetivo de que
converjan a la solución exacta.
(k )
b (k )
)
! a(1)
11
#
# 0
#
"
=#
# 0
#
# "
#
" 0
(1)
(1)
(1)
a12 ! a1k ! a1n
( 2)
( 2)
( 2)
a22 ! a2k ! a2n
"
0
#
"
#
"
(k)
(k)
! akk ! akn
#
0
(
"
#
"
(k)
(
! ank ! annk)
b1(1) $
&
b2(2) &
&
" &
bk(k ) &
&
" &
&
bn(k ) %
)
que inicialmene sería: A(1) b(1) = ( A b )
6
8
(
) (
1. Para k=1,2,…,n-1, "" A (k ) b(k ) ! A (k +1) b(k +1)
a) Si
(k )
akk
)
•
como sigue:
! 0 (pivote), entonces:
posible sin intercambio de filas?
•
i. Formamos la matriz de transformación:
"1
$"
$
$0
Lk = $
0
$
$"
$# 0
!
#
0
"
!
1
! !lk+1,k
#
!
"
!lnk
(
(
Teorema 3.1
Sea el sistema nxn, Ax=b, con det(A)!0; entonces el
método de Gauss puede completarse sin intercambio de
las filas si, y sólo si,
! a11 … a1k $
det # ! " ! & ' 0
#
&
" ak1 # akk %
)
(k +1)
b (k +1) = Lk A (k!) b (k ) donde A (k+1) tiene
ii. Entonces: A
ceros bajo la diagonal en las columnas 1,2,…, k."""""
9
(k )
b) Si akk
= 0 , entonces:
(k )
• Buscamos el primer elemento no nulo a jk (j > k)
• Intercambiamos las filas j y k-ésima en
(las notamos igual)
(A
(k )
b (k )
)
• Procedemos como en el caso anterior.
2. Resolvemos el sistema triangular resultante: Ux = b *
si en el caso b) todos los posibles pivotes son nulos
¿qué ocurre?
0 ! 0%
" # "'
'
)
a(k
0 ! 0'
jk
!!!con!!l
=
,!!! j > k
jk
(k )
1 ! 0'
akk
'
" # "'
0 ! 1 '&
)
¿cuándo podemos saber si el método de Gauss es
donde
U = A (n) ,!!!b* = b (n)
10
k = 1, 2,…, n
11