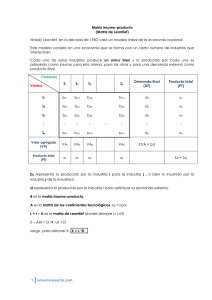
UN MODELO INSUMO PRODUCTO (MIP) COMO INSTRUMENTO

Banco Central de Venezuela
Colección Economía y Finanzas
Serie Documentos de Trabajo
UN MODELO
INSUMO
PRODUCTO (MIP)
COMO
INSTRUMENTO
DE ANÁLISIS
ECONÓMICO
ELVIS HERNÁNDEZ*
[Nº 69]
Mayo, 2005
© Banco Central de Venezuela, Caracas, 2005
Gerencia de Investigaciones Económicas
Producción editorial
Gerencia de Comunicaciones Institucionales
Departamento de Publicaciones
Torre Financiera, piso 14, ala sur.
Avenida Urdaneta, esquina de Las Carmelitas
Caracas 1010
Teléfonos: 801.8075 / 801.8063
Fax: 536.93.57
[email protected]
http: //www.bcv.org.ve
RIF: G-20000110-0
Las opiniones y análisis que aparecen
en la Serie Documentos de Trabajo
son responsabilidad de los autores
y no necesariamente coinciden
con las del Banco Central de Venezuela.
Se permite la reproducción parcial o total
siempre que se mencione la fuente
y no se modifique la información.
ÍNDICE
RESUMEN ................................................................................................. 10
INTRODUCCIÓN ...................................................................................... 11
I. LINEAMIENTOS GENERALES
DEL MODELO INSUMO-PRODUCTO (MIP) ..................................... 16
I.1 Antecedentes ............................................................................. 16
I.2 El Sistema de Cuentas Nacionales (SCN)
y el Modelo Insumo-Producto (MIP) ............................................. 18
I.3 Programa de Actualización de las
Estimaciones Macroeconómicas (Pracem). .................................... 21
I.4 Unidades estadísticas y los sistemas
de clasificación para la reunión de datos
necesarios para la COU y la Matriz Insumo-Producto. .................. 22
I.5 Conceptos básicos empleados en los COU ............................... 27
I.6 Cuadros de Oferta y Utilización (COU)
y el Modelo Insumo-Producto (MIP) ............................................. 30
I.6.1 Estructura del Cuadro de Oferta
y Utilización de la economía venezolana. ................................. 31
II. El MODELO INSUMO-PRODUCTO (MIP) COMO
INSTRUMENTO DE ANÁLISIS ECONÓMICO ................................ 37
II.1 Visión general del MIP............................................................. 37
II.2 Usos y limitaciones del Modelo Insumo-Producto .................. 40
II.3 Aspectos relevantes de experiencias en insumo
producto. ........................................................................................ 47
II.3.1 La Matriz Insumo-Producto para
Venezuela (1981 y 1984).......................................................... 35
II.3.2 La Matriz Insumo-Producto del Caribe
colombiano. .............................................................................. 56
II.3.3 Un análisis Input-Output de la economía
balear. ....................................................................................... 58
II.4. Bases para otros estudios........................................................ 60
II.4.1 Análisis estructural a partir de la
Teoría de las Redes Sociales .................................................... 61
II.4.2 Construcción de Modelos de Equilibrio
General Computable. ............................................................... 62
II.4.3 Construcción de Matrices de
Contabilidad Social (MCS, SAM). .......................................... 64
II.4.4 Construcción de Modelos Dinámicos
de Insumo-Producto. ............................................................... 66
II.4.5 Estudios econométricos. ................................................ 67
II.4.6 Análisis y construcción de
multiplicadores multisectoriales. .............................................. 68
III. LA PRODUCCIÓN SECUNDARIA Y EL MODELO INSUMOPRODUCTO (MIP) .............................................................................. 70
III.1 Visión general. ........................................................................ 70
III.2 Clases de productos secundarios. ........................................... 72
III.3 Separación de las empresas en unidades
homogéneas. ................................................................................... 74
III.3.2 Normas generales del SCN para
crear un establecimiento separado. ........................................... 75
III.3.2 Separación de la construcción por
cuenta propia y las actividades integradas
verticalmente. ........................................................................... 77
III.3.3 Distribución de los costos de
actividades auxiliares a los
establecimientos. ....................................................................... 77
III.3.4 Actividades auxiliares con ventas. ................................. 78
III.3.5 El método de la redefinición. ......................................... 79
III.4 Tratamiento de los productos secundarios que se originan
en la tecnología de producto........................................................... 79
III.4.1 Métodos manuales o mecánicos. ................................... 80
III.4.2 Métodos matemáticos. .................................................. 82
IV. ANÁLISIS TEÓRICO DEL MODELO INSUMO-PRODUCTO
(MIP) DE LEONTIEF. .......................................................................... 95
IV.1 Funciones de producción. ....................................................... 95
IV.2 Rendimientos de escala. .......................................................... 96
IV.3 Función de Producción de Leontief. ....................................... 97
IV.4 Modelo Matricial Insumo-Producto. ...................................... 99
IV.4.1 Deducción analítica del MIP. ....................................... 101
IV.4.2 Cálculo de la Matriz Insumo-Producto Inversa. .......... 107
IV.4.3 Determinación del empleo. .......................................... 112
IV.4.4 Determinación de precios. ........................................... 116
IV.4.5 Determinación de los sectores claves. ......................... 119
V. BASES METODOLÓGICAS .............................................................. 124
V.1 Módulo 1: Método de agregación de
productos, actividades y variables del COU. ................................ 125
V.2 Módulo 2: Método de corrección de
los productos secundarios y cálculo
de la inversa. ................................................................................. 130
V.3 Módulo 3: Determinación de los
requerimientos primarios de personal
ocupado y formación bruta de capital. .......................................... 134
V.4 Módulo 4: Determinación de los sectores
claves de la economía a partir del MIP. ........................................ 136
V.5 Módulo 5: Determinación del Producto
Interno Bruto por la vía del ingreso, el
gasto y la producción. ................................................................... 136
VI. RESULTADOS. .................................................................................. 143
VI.1 La Matriz de Coeficientes Técnicos
producto por producto. ................................................................ 144
VI.2 La Matriz de Requerimientos Directos
e Indirectos (Matriz inversa de Leontief). .................................... 147
VI.3 El Producto Interno Bruto. .................................................. 150
VI.4 Simulación de impactos observados
en la demanda final. ...................................................................... 154
VI.5 El Producto Interno Bruto (Vía del Gasto,
Producción e Ingreso). ................................................................. 157
VI.6 Determinación de los sectores claves
de la economía a partir del MIP. ................................................... 159
CONCLUSIÓN ........................................................................................ 162
APÉNDICE .............................................................................................. 165
BIBLIOGRAFÍA ...................................................................................... 184
Resumen
La economía es un sistema complejo de interrelaciones
entre individuos, empresas y otras organizaciones como
el gobierno y las instituciones sin fines de lucro. Desde
el punto de vista de la producción de bienes y servicios
de la economía, existen sectores relacionados entre sí
a través de una extensa red de transacciones, entre
ellos se encuentran los que tienen como función u
objetivo, producir para suministrar bienes y servicios a
otros sectores en calidad de insumos, y otros que
producen directamente para satisfacer el consumo final.
El Modelo de Insumo Producto (MIP), es una
herramienta que permite evaluar las interrelaciones e
interdependencias existentes entre los diferentes
sectores productivos de una economía, cuyos datos son
fáciles de encajar en los modelos macroeconómicos,
destinados a analizar las relaciones entre la demanda
final y los niveles de producción por actividades
económicas. Es por ello, que la integración del MIP con
los nuevos enfoques metodológicos y analíticos
proporcionados por el Sistema de Cuentas Nacionales
de 1993 (SCN), constituye una fuente importante de
consistencia y aplicación, en función de ampliar la
disponibilidad de información estadística-económica,
particularmente para los organismos públicos y privados
dedicados a la planificación y elaboración de políticas
económicas para el desarrollo.
Adicionalmente, el análisis insumo-producto, busca
ampliar la interpretación de las estadísticas económicas
resultantes de la implementación del nuevo (SCN) y del
nuevo año base 1997, en virtud de profundizar el uso
de los resultados hacia un análisis mayor de las
estructuras productivas sectoriales, y cómo éstas se
encuentran influenciadas por cambios en la demanda
final (supuestos exógenos). En este sentido, se intenta
identificar los sectores claves que dinamizan el proceso
productivo en la economía venezolana, para así
determinar aquellas actividades hacia donde tienen que
dirigirse las políticas sectoriales e industriales.
Palabras clave: insumo-producto/interrelaciones
intersectoriales/estructuras productivas.
Abstract
The economy is a complex system of interrelations
among individuals, companies and other organizations
like the government and nonprofit institutions. Regarding
the production of goods and services in the economy,
there are sectors related to each other through an
extensive net of transactions. Among them we can find
those who have the objective of producing in order to
supply goods and services to other sectors as inputs,
and others who produce directly to satisfy final
consumption.
The Input- Output Model (IOM) is a tool which allows
evaluating the interrelations and interdependences
among the different productive sectors of an economy,
whose data are easy to fit into the macroeconomic
models, destined to analyze the relationships between
the final demand and the levels of production by
economic activities. That is why the integration of the
IOM with the new methodological and analytical view,
provided by the System of National Accounts 1993
(SNA), represents an important source of consistency
and application, aiming to extend the availability of
statistic-economic information, particularly to public and
private entities in charge of planning and working out
economic policies to encourage development.
Additionally, the input-output analysis, seeks to extend
the interpretation of the economic statistics arising from
the implementation of the new (SNA) and of the new
base period 1997, by virtue of deepening the use of the
results towards a greater analysis of the sectorial
productive structures, and how these are influenced by
changes in the final (exogenous suppositions) demand.
In that respect, we have been trying to identify the key
sectors in charge of boosting the productive process in
the Venezuelan economy in order to determine the
activities towards which the sectorial and industrial
policies should be guided.
Key words: input-output/ intersectorial interrelations /
productive structures.
INTRODUCCIÓN
La economía es un sistema complejo donde interactúan los individuos,
las empresas y otras organizaciones en un sistema global, y sus acciones (individuales o colectivas) están entrelazadas como el resultado de
su comportamiento; en este sentido, se hace necesario la construcción
de modelos económicos para caracterizar y analizar estos fenómenos;
el poder de éstos en la interpretación económica se deriva en la supresión de detalles que delimite rasgos esenciales e importantes sobre la
realidad que se intenta comprender. En este complejo sistema, existen
actores económicos interactuando entre sí en una extensa red de transacciones, unos que tienen como función u objetivo producir para suministrar los bienes y servicios a otros sectores en calidad de insumos
y otros destinan su producción hacia el consumidor final.
En 1936, Leontief propuso un modelo sectorial de Insumo-Producto
con vínculos en precios y cantidades, donde los bienes y servicios de
cada sector son homogéneos, cada uno de ellos mantiene inalterada su
estructura y precios relativos de los insumos; en este sentido, se comprende que variaciones en los coeficientes técnicos están asociados a
modificaciones derivadas del progreso tecnológico. En principio, el
Modelo de Insumo-Producto (MIP) tenía como propósito analizar las
relaciones e interdependencias existentes entre los diversos sectores
de una economía; por otro lado, el sistema en cuestión es un conjunto
de ecuaciones lineales cuyos coeficientes numéricos (coeficientes técnicos) representan los parámetros del sistema y las características estructurales de una economía.
Para Venezuela existe cierta experiencia en la elaboración de matrices
Insumo-Producto, aunque su aplicación ha sido bastante reducida debido a la falta de continuidad y la poca experticia para adoptar los
nuevos cambios del Sistema Integrado de Compatibilización Estadística. Las mismas fueron elaboradas por el Instituto de Urbanismo de la
Universidad Central de Venezuela (Iuucv), el Instituto Venezolano de
11
Planificación (Iveplan), la Dirección de Mediano y Largo Plazo de
Cordiplan e Iveplan; y en este sentido, también destaca la obtención
de las matrices de Insumo-Producto por parte de Lino Clemente y Alejandro Puente en el BCV, como un importante aporte en la evaluación
de las estructuras productivas de la economía venezolana.
La integración del Modelo de Insumo-Producto con los nuevos enfoques metodológicos y analíticos proporcionados por el Sistema de
Cuentas Nacionales de 1993 (SCN) en Venezuela, es un importante
avance para ampliar la disponibilidad de información estadística-económica, particularmente para los organismos públicos y privados
dedicados a la planificación y el desarrollo. Por otro lado, facilita la
interpretación de las estadísticas económicas resultantes de la implementación del nuevo SCN 1993 y el Año Base 1997, profundizando el
uso de los resultados macroeconómicos y sirviendo de marco coordinador de las estadísticas económicas, en la medida que da coherencia
a las clasificaciones y definiciones utilizadas dentro de este marco contable.
De igual manera, la necesidad de observar la interrelación intersectorial
y el comportamiento de la economía real para el caso venezolano, bajo
el supuesto de la no-existencia de choques tecnológicos y conjuntamente en presencia de un equilibrio contable, en el que la oferta total
es igual a la demanda total se intenta responder: ¿Es posible anticipar
la dirección de los impactos que tienen las variaciones de la demanda
final sobre la producción sectorial, mediante una relación Insumo-Producto?
Esta investigación tiene como objetivo general, mostrar la importancia
para el análisis económico del desarrollo de un Modelo Insumo-Producto (MIP) que caracterice la economía venezolana, como un instrumento adicional de interpretación estadístico-económico; para ello, se
busca sintetizar los rasgos metodológicos básicos del modelo, basándose en las especificaciones generales del SCN 1993 y en la estructura
de Cuadros de Oferta y Utilización para Venezuela. En el mismo orden
12
de ideas, es necesaria la exposición del marco analítico del MIP como
un modelo de programación lineal, que facilite la observación de las
interrelaciones intersectoriales, la determinación del Producto Interno
Bruto por el enfoque del ingreso, el gasto y la producción a partir de
variaciones exógenas de la demanda final; y en efecto, enunciar los
usos, limitaciones y bases para otros estudios del MIP como instrumento de análisis económico y planificación sectorial.
La hipótesis básica de este trabajo, es que el Modelo Insumo-Producto
con precios dados permite anticipar la dirección del cambio en el PIB
sectorial y el PIB total, a partir de variaciones exógenas en los componentes de demanda final.
El MIP a desarrollar y analizar, está enmarcado dentro de la información del flujo de bienes y servicios que se genera en la economía venezolana; cuyos datos recopilados provienen de los resultados de la
culminación del Programa de Actualización de las Estimaciones
Macroeconómicas (Pracem) e implementación del nuevo Año Base
1997, por parte de la Gerencia de Estadísticas Económicas del Banco
Central de Venezuela; y en este sentido es preciso mencionar que estos
datos son preliminares y están sujetos a revisión.
El trabajo se estructurará de la siguiente manera:
• En la primera parte se hará referencia a los antecedentes históricos
del modelo, sus primeras aplicaciones y algunas premisas básicas
de estudios recientes, por otro lado, se desarrollará el papel del Programa de Actualización de las Estimaciones Macroeconómicas
(Pracem) y la implementación del nuevo Sistema de Cuentas Nacionales de 1993 (SCN) como un sistema de contabilidad nacional y de
medición macroeconómica; de igual manera, se hará alusión a la
construcción del Cuadro de Oferta y Utilización (COU) de la economía venezolana y su relación en el desarrollo del Modelo InsumoProducto (MIP).
13
• El segundo apartado, hace referencia a una visión general del MIP y
se expone algunos casos relevantes y necesarios de mencionar sobre experiencias del uso de estos modelos para el análisis e interpretación económica. También se expondrá, algunos usos y limitaciones del Modelo Insumo-Producto, y se hará mención de algunas
bases para otros estudios e investigaciones que se pueden derivar
del desarrollo y elaboración de matrices Insumo-Producto.
• La tercera parte, hace referencia a un análisis extenso sobre el tratamiento de los productos secundarios dentro del Modelo InsumoProducto, ya que lo ideal en la construcción de los cuadros simétricos Insumo-Producto es contar con aquellas actividades que producen un único bien y así conservar la homogeneidad en la función de
producción; con ello se expone los diferentes métodos que utilizan
los compiladores de matrices Insumo-Producto para corregir la presencia de productos secundarios.
• En el cuarto apartado, se muestra un desarrollo analítico para llegar
desde la función de producción microeconómica de Leontief a la
función macroeconómica de Insumo-Producto, por otro lado se
muestra el papel de la producción secundaria, la inversa de Leontief,
determinación de los requerimientos primarios de Personal Ocupado (PO), Formación Bruta de Capital (FBK) y obtención de los Sectores Claves de la economía con la ayuda de los índices de
eslabonamientos.
• El capítulo cinco, proporciona el marco metodológico para desarrollar y analizar el MIP como un instrumento de análisis económico;
enmarcándose en primer lugar en el método de agregación de productos, actividades y variables del Cuadro de Oferta y Utilización
(COU), que permite trabajar la matriz Insumo-Producto de una forma más reducida y así facilitar el manejo de los datos. En segundo
lugar, se expone el método de corrección de los productos secundarios
y
14
cálculo de la inversa; en tercer lugar la determinación de los requerimientos primarios de personal ocupado y formación bruta de capital; y en cuarto lugar, se incorpora la metodología usada en la determinación de los sectores claves de la economía.
• Para finalizar, en la sexta parte se presentará los principales resultados para la economía venezolana del uso del Modelo Insumo-Producto como instrumento de análisis económicos y en la séptima parte se expondrá las conclusiones y recomendaciones del trabajo de
investigación.
15
I.
LINEAMIENTOS GENERALES
DEL MODELO INSUMO-PRODUCTO (MIP)
El presente capítulo busca proporcionar una visión general de los antecedentes más relevantes del MIP y la adopción del nuevo Manual del
Sistema de Cuentas Nacionales (SCN) de 1993, como un marco contable aceptado internacionalmente para mejorar la calidad y homogeneidad de las estadísticas económicas presentadas en los países, en
este sentido, desempeña una función importante en la elaboración y
presentación de los datos económicos en un formato destinado a su
análisis, a la toma de decisiones y la formulación de la política económica.
Por otro lado, se hace mención al papel del Banco Central de Venezuela (BCV) y la Gerencia de Estadísticas Económicas de esta misma
institución, en la culminación del Programa de Actualización de las
Estimaciones Macroeconómicas (Pracem) e implementación del nuevo Año Base, 1997. También, se desarrolla un análisis sobre las unidades estadísticas y los sistemas de clasificación para la reunión de datos
necesarios para el Cuadro de Oferta y Utilización (COU) y la Matriz
Insumo-Producto, se expone los conceptos básicos empleados el (COU)
y por último, se expone el Cuadro de Oferta y Utilización (COU) de la
economía venezolana, describiendo su estructura y sus principales variables, que sirven de insumo en la construcción del Modelo de InsumoProducto.
I.1 Antecedentes
Existe una gran evidencia, que François Quesnay (1736) con su
“Tableau Économique” fue el primero en ocuparse del estudio de las
interrelaciones que se dan entre los distintos sectores productivos, por
lo cual es considerado el primer antecedente en los estudios InsumoProducto; además, la inspiración de los trabajos modernos en este campo se inician con León Walras (1926), seguido por W. Leontief en
16
1936 y 1941, quien realmente sintetiza estos enfoques, para elaborar
un modelo que permitiera realizar trabajos empíricos, denominado
Modelo Insumo-Producto (MIP) (Clemente y Puente, 1989).
Por otro lado, Quan Kiu (1996, p.145) señala que la primera aplicación del análisis Insumo-Producto tiene su origen en los ensayos
François Quesnay hacia 1750, estos fueron realizados en Francia con
el fin de medir los flujos e interrelaciones de la actividad económica,
pero es recientemente, en las décadas de 1940-1950, cuando Wasilly
Leontief, con Richard Stone y el grupo de Oslo, diseña y perfecciona
un sistema de cuentas globales para medir la actividad económica de
una nación; estos modelos fueron aceptados y adoptados por la Organización de las Naciones Unidas (ONU) y se han venido perfeccionando a través de reuniones y acuerdos internacionales.
El modelo de Leontief simplifica el sistema de Walras para poder obtener, una observación separada de las transacciones interindustriales en
la economía y del conjunto de parámetros que conforman el modelo.
Asimismo, Leontief utilizó el supuesto walrasiano de “coeficientes de
producción fijos”, en lugar de tener en cuenta el efecto sustitución
entre los insumos (Clemente y Puente, 1989). Sin embargo, a partir de
los trabajos de Armington (1969) se han logrado incorporar coeficientes técnicos que son función de los precios, de los bienes domésticos y
de los bienes importados.
En lo esencial, el aporte principal del MIP según las Naciones Unidas
(2000, p. 3) y Kohli (2001), es mostrar las relaciones de compras y
ventas entre distintos consumidores de una economía en un marco analítico que facilita las proyecciones y los análisis económicos. Bajo esta
perspectiva, el modelo supone que los insumos necesarios para la elaboración de un bien o producto está relacionado por una función de
producción de coeficientes lineal y fijo (al menos en el corto plazo).
17
Por último, es conveniente anotar que la técnica de Insumo-Producto
de Leontief, fue construida inicialmente para el análisis nacional de las
modificaciones estructurales de la economía norteamericana. No obstante a pesar de sus restricciones, esta técnica ha sido ampliamente
utilizada por varias razones, entre ellas, destaca la posibilidad de
hacer una representación holística del sistema económico, es un instrumento operativo de la teoría del equilibrio general que enlaza el
análisis microeconómico de corte neoclásico y la teoría macroeconómica
de visión keynesiana (Laguna, 2003). Gracias a este aporte, las Naciones Unidas (2000, p. 3) menciona que Leontief recibió el premio Nobel
de Economía en 1973 por la creación de los métodos Insumo-Producto
y luego se integró el marco Insumo-Producto en el sistema de cuentas
nacionales, integración que fue publicada en 1968 por las Naciones
Unidas como “A System of National Account, Studies in Methods”.
I.2 El Sistema de Cuentas Nacionales (SCN)
y el Modelo Insumo-Producto (MIP)
En la historia del SCN se combinan dos trayectorias: el desarrollo de
la contabilidad nacional y la internacionalización de las preocupaciones estadísticas, para lograr una comparabilidad de las estadísticas
económicas y el desarrollo de normas y directrices internacionales que
se remonta al menos a 1928, en este sentido, urgía a los países a considerar la ampliación de las estadísticas oficiales con el fin de facilitar
la elaboración de las estimaciones del ingreso nacional a intervalos
regulares. Es así como, se ha expandido y desarrollado su estudio para
alcanzar esa comparabilidad y esa aplicación en todas las economías
del mundo (FMI, OCDE, Naciones Unidas, 1993).
La adopción del SCN, 1993 fue recomendada unánimemente al Consejo Social de las Naciones Unidas, por su Comisión de Estadística en
su vigésimo-séptima sesión, celebrada en Nueva York, del 22 de febrero al 3 de marzo de 1993. El desarrollo de nuevas técnicas para
poder analizar y determinar de una manera muy acertada el comportamiento de la economía es uno de los retos de los hacedores de política
económica. Entre estas nuevas técnicas esta la elaboración de las esta-
18
dísticas económicas y otras estadísticas conexas, donde, El Sistema de
Cuentas Nacionales (SCN) de 1993, representa un gran avance de la
contabilidad nacional. Por eso, el Consejo recomienda a los Estados
miembros el uso del SCN, 1993, como la norma internacional para la
elaboración de las estadísticas económicas y otras estadísticas conexas,
como una herramienta analítica y como una forma internacional de
datos de contabilidad nacional comparables (FMI, OCDE, Naciones
Unidas, 1993).
“El Sistema de Cuentas Nacionales (SCN) consta de un conjunto coherente, sistemático e integrado de cuentas macroeconómicas, balances y cuadros basados en un conjunto de conceptos, definiciones y
clasificaciones y reglas contables aceptadas internacionalmente”1 además, ofrece un amplio marco contable dentro del cual pueden elaborarse y presentarse datos económicos en un formato destinado a su
análisis, a la toma de decisiones y la formulación de la política económica, conjuntamente con una visión general del comportamiento económico de los sujetos o agentes como resultado de la actividad
económica con sus diferentes interrelaciones. Por otro lado, incluye un
conjunto integrado de cuadros o matrices de oferta y utilización que se
analizará más adelante, así como cuadros o matrices simétricos de
Insumo-Producto. Ellos proporcionan un análisis detallado del proceso de producción y utilización de bienes y servicios (productos) y del
ingreso generado en dicha producción.
La integración del Insumo-Producto en el sistema global de cuentas
nacionales y su relación está enfocada con las cuentas de bienes y
servicios y con la secuencia abreviada de cuentas de industrias. Los
cuadros de oferta y utilización y por consiguiente, los cuadros simétricos2 Insumo-Producto, sirven para proporcionar una base más detallada para el análisis de las industrias, de las actividades económicas y de
1
FMI, OCDE, Naciones Unidas (1993), Sistema de Cuentas Nacionales de 1993, pág. 1.
2
Simétrico, significa que las mismas clasificaciones o unidades (es decir, la apertura de los
grupos de clasificación corresponde al mismo número de filas y columnas), en cambio los
cuadros de oferta y utilización tienden a ser no simétricos (es decir, el número de filas no
es igual al número de columnas).
19
los productos en el sistema mediante la desagregación de las cuentas
de producción y generación del ingreso, junto con el traslado de las
cuentas de bienes y servicios al cuadro simétrico Insumo-Producto.
Estos cuadros proporcionan un marco que permite comprobar la consistencia de las estimaciones de los flujos de bienes y servicios obtenidas de fuentes estadísticas muy diferentes: encuestas industriales,
encuesta del gasto de los hogares, encuestas de inversión, estadísticas
del comercio exterior, etc.; particularmente los cuadros Insumo-Producto, sirven de marco coordinador para dar coherencia de las definiciones y clasificaciones utilizadas, asegurando la coherencia numérica
de los datos obtenidos de diversas fuentes y la integración a los modelos macroeconómicos destinados a analizar las relaciones entre la demanda final y los niveles de producción de las industrias (FMI, OCDE,
Naciones Unidas, 1993: pág. xiii).
Desde la perspectiva más general, el SCN es un sistema de propósitos
múltiples como ya se ha indicado, destinado al análisis económico, a
la toma de decisiones y a la formulación de la política económica,
cualquiera que sea la estructura económica o el grado de desarrollo
económico alcanzado por un país. Los conceptos y definiciones básicos del sistema dependen de un razonamiento y de unos principios
estadísticos-económicos que tienen que ser universalmente válidos e
invariantes con respecto a las circunstancias económicas particulares
en que se apliquen (FMI, OCDE, Naciones Unidas, 1993: párr. 1.29).
El sistema pretende, primordialmente, ofrecer datos a niveles de agregación diferentes que satisfagan las necesidades de los analistas y de
los diseñadores de las políticas interesados en el comportamiento de la
economía; por ejemplo, los factores responsables de los grandes
desequilibrios del mercado, como la inflación y el desempleo. Dentro
de este marco, el sistema es un acuerdo encaminado a proporcionar los
máximos beneficios a diferentes clases de usuarios y puede, por lo
tanto, que no sea el óptimo para cualquier otra finalidad tomada aisladamente (FMI, OCDE, Naciones Unidas, 1993: párr. 1.82).
20
I.3 Programa de Actualización de las Estimaciones
Macroeconómicas (PRACEM)
El Directorio del Banco Central de Venezuela (BCV) aprobó el
26-07-1995 la ejecución del Pracem como programa extraordinario de
alcance plurianual, para lograr una revisión exhaustiva y una mejora
considerable en la medición de las estadísticas económicas que produce este Instituto, tanto para usuarios nacionales como internacionales.
La justificación de llevar a cabo este programa, era incorporar los nuevos enfoques de los manuales internacionales del Sistema de Cuentas
Nacionales (SCN) y Balanza de Pagos (BP) de 1993, por otro lado,
tenemos la obsolescencia del año base 1984 como año de referencia
para las estimaciones macroeconómicas que obligaba a adoptar otro año
base que fuera más representativo y la necesidad de mejorar y actualizar los indicadores estadísticos en función de hacer un mejor seguimiento y análisis al comportamiento de la economía venezolana.
A finales de 1996 se inició el Pracem, cuyos objetivos fue adoptar los
manuales del SCN de 1993, BP de 1993 y la CIIU de 1990, cambiar el
año base del SCN y del IPC, mejorar las estadísticas existentes y obtener nuevos indicadores económicos, en donde se eligió el año 1997
como año base, debido a las condiciones económicas e información
estadística disponible, sumado a un año en la cual no se manifestó
movimientos bruscos y choques erráticos sobre la actividades económicas. Por otro lado, el levantamiento masivo de información para el
año base e inmediatos posteriores se realizó mediante: trabajos directos BCV, convenios con organismos públicos y contratos con empresas privadas especializadas y de gran relevancia económica. Una primera fase de culminación se refleja en la consolidación y evaluación
de estimaciones del SCN y BP (serie 1997-2001) para diciembre de
2003, logrando con ello mostrar el gran cúmulo de información económica compatibilizada y armonizada de acuerdo a los nuevos enfoques
analíticos y metodológicos de relevancia y concordancia internacional.
21
Las mejoras metodológicas y analíticas van desde el levantamiento
de la información sectorial, luego un complejo y estricto proceso de
validación e integración de datos provenientes de diferentes fuentes,
realización de matrices intra e inter sectoriales que parten de las transacciones corrientes hasta las financieras de la economía venezolana.
Este proceso dirigido al mejoramiento de las estimaciones
macroeconómicas generó un relevante nivel de las actividades económicas, apertura de sectores, tipos de bienes y servicios e instrumentos
financieros que enriquecen tanto el análisis como la evaluación de los
resultados.
I.4 Unidades Estadísticas y los Sistemas de Clasificación para la reunión
de datos necesarios para la COU y la Matriz Insumo-Producto
Uno de los primeros y principales aspectos a desarrollar por parte del
Pracem fue precisamente la definición de todos los clasificadores necesarios para la elaboración de las estadísticas, pudiendo clasificar a
las industrias, a los productos, a las instituciones y a las cuentas. Es así
como se utilizaron como base para la definición de estos clasificadores
los ya dispuestos por los organismos multilaterales, con la finalidad
que las estadisticas mantengan los estandares que le permitan la
comparabilidad internacional. Sin embargo, se requirió de una
desagregación más amplia y detallada con adaptaciones particulares
para el caso de Venezuela, elaborando clasificadores propios que permitieran satisfacer las demandas de las estadísticas nacionales.
22
Clasificación
Industrial (CIIU)
Clasificación Central
de productos (CCP)
Actividades Económicas
Consumo Intermedio
Industrias
Demanda Final
Producción Industrial
Gasto de consumo final
Valor Agregado
Formación bruta de capital
Clasificación
Institucional
Empresas (la menor
unidad jurídica)
Unidades de gobierno
ISLSH
Hogares
Exportaciones
Importaciones
Estos clasificadores permiten establecer todo el marco operativo y de
funcionamiento de las cuentas determinando de una manera ordenada
los criterios de agregación y desagregación de las mismas, así como el
cruce entre cuentas, variables y sectores.
Clasificación Industrial Internacional Uniforme (CIIU)
La unidad estadística para las actividades o industrias que recomienda
el SCN es el establecimiento, que puede realizar una o más actividades secundarias, pero a una escala menor comparada con la actividad
principal. Si una empresa tiene más de un establecimiento, cada uno
de ellos será tratado en forma separada.
Las categorías en que se pueden clasificar los datos sobre las actividades o las industrias se encuentran en la publicación de las Naciones
Unidas titulada Clasificación Industrial Internacional Uniforme de
todas las actividades económicas. En la actualidad tiene 17 categorías
23
principales (codificadas con letras), 60 divisiones (con códigos de dos
dígitos), 169 grupos (con códigos de tres dígitos) y 291 clases (con
códigos de cuatro dígitos) y en consecuencia, es posible clasificar todas las actividades económicas de un país. El propósito fundamental
de todo esto, es permitir establecer un conjunto jerárquico de categorías que permitan analizar y agregar estadísticas de producción de acuerdo a sus actividades y de igual manera vincular la manera como está
organizado el proceso económico3.
Sistema de Clasificación de Productos
En este tipo de clasificación se recomienda la Clasificación Central de
Productos (CCP), para clasificar productos que son el resultado de las
actividades de producción nacionales e importaciones procedentes de
fuentes no residentes. La dimensión del marco Insumo-Producto del
SCN puede basarse en la CCP que abarca tanto bienes como servicios
que son resultado de la actividad económica. La clasificación detallada consta de 10 secciones (código de un dígito), 69 divisiones (código
de dos dígitos), 291 grupos (código de tres dígitos), 1.036 clases (código de cuatro dígitos) y 1.787 subclases (código de cinco dígitos).
Esta clasificación está perfectamente cruzada con la CIIU lo que permite a su vez clasificar los productos al nivel de actividades, elemento
indispensable para mantener la propiedad de agregación y
desagregación de cuentas y variables. Por ejemplo, para obtener el
cuadro simétrico de Insumo-Producto de los cuadros productos por
producto o industria por industria a partir de los cuadros de oferta y
utilización, la clasificación de las actividades económicas debe ser la
misma que la clasificación de productos.
Es así como este clasificador, CCP, fue el utilizado como base para
definir el Clasificador de Productos de Venezuela (CPV), realizándole
3
En los cuadros de oferta y utilización; “industria”, se refiere al tipo de actividad en el que
se agregan todas las unidades que realizan actividades productivas en específico.
24
algunas adaptaciones propias de los productos más representativos de
este país, con la finalidad de clasificarlos de acuerdo a las características físicas e intrínsecas de los productos y que en la medida de lo
posible los bienes y servicios individuales contengan aquellos que son
producidos por una única industria, aspecto fundamental en la construcción del Insumo-Producto.
Clasificación de sectores institucionales
Una unidad institucional según Naciones Unidas (2000): “puede ser
un hogar o entidad jurídica o social”. Por otra parte, una unidad institucional se le define como “una entidad económica que tiene capacidad, por derecho propio, de poseer activos, contraer pasivos y realizar
actividades económicas y transacciones con otras entidades” (FMI,
OCDE, Naciones Unidas, 1993). El SCN establece cinco categorías
amplias de sectores institucionales internos; el sector de las sociedades no financieras, el sector de las sociedades financieras, el sector
gobierno general, el sector hogares y el sector de las instituciones sin
fines de lucro que sirven a los hogares.
Sirviendo de base estas cinco categorías, se clasificaron todo el conjunto de instituciones existentes dentro de la economía venezolana
llegando a disponer de un total de 91 sectores institucionales, dentro
de los cuales 74 se les procesa información; cumpliendo de igual
forma con todas las características para lograr la agregación y
desagregación de las mismas. Es importante destacar que adicionalmente el SCN diferencia entre los conceptos de sociedades constituidas en sociedades de aquellas no constituidas en sociedades,
formando el sector formal e informal respectivamente de la economía.
25
Cuentas de Producción
127 actividades económicas
(sectores público y privado)
(sociedades y no sociedades)
Valor bruto de producción
Consumo intermedio
Valor agregado bruto
Armonización de oferta y
demanda para 300 productos, a
precios corrientes, constantes;
precios implícitos
Cuentas de Bienes y Servicios
Economía interna
Transacciones
Sector público
Sector privado
Resto del
mundo
Mundo
Cuentas corrientes
Intereses
Dividendos
Retiros de las cuasisociedades
Utilidades reinvertidas de la inversión
directa extranjera
Renta de la propiedad atrib. A los
titulares de pólizas de seguro
Renta de la tierra
Contribuciones sociales efectivas de los
empleados
Contribuciones sociales de los
asalariados
Contribuciones soc. Imputadas
Primas netas de seg. No de vida
Indemn. De seguros no de vida
Transferencias corrientes div.
74 sectores institucionales
(versus 37 en PCAB)
13 matrices de transacciones
(versus 9 en PCAB)
Transferencias de capital recibidas
Economía interna
Transacciones
Sector público
Sector privado
Resto del
mundo
Mundo
Cuenta financiera
Oro monetario y deg
Dinero legal y depósitos
74 sectores institucionales
Valores distintos de acciones
(versus 37 en PCAB)
Préstamos
68 matrices de instrumentos
Acciones y otras
participaciones de capital
(versus 19 en PCAB)
Reservas técnicas de
seguros
Otras cuentas por
Cobrar/pagar
cobrar/pagar
Nota: Obtenido de las presentaciones de la exposición de resultados del Departamento de Cuentas Macroeconómicas del
BCV, 2004.
26
Clasificación de cuentas
Por último, la estructura de cuentas y variables del SCN disponen de
su propia forma de clasificación, la cual fue base fundamental para la
estructuración de las cuentas integradas en el caso de Venezuela. Sin
embargo, estas fueron sujetas de adaptación a las realidades propias
del país, y en consecuencia, los instrumentos que según el manual están dentro de cada clasificación y que son instrumentos propios de esta
economía, para las cuales se observa aproximadamente 537 conceptos
diferentes.
I.5 Conceptos básicos empleados en los COU4
Considerando el marco referido por los clasificadores, el cual nos permite
poder ir desde la unidad primaria estadística, denominada establecimiento, hasta llegar a la agregación y consolidación de resultados, como
lo refleja el COU. Es en efecto, el insumo principal del MIP, para ello
es importante considerar algunos conceptos básicos manejados en este
Cuadro.
Industria: Como se dijo anteriormente, una industria consiste en un
conjunto de establecimientos que se dedican a una sola actividad. Desde
el punto de vista de SCN, una industria está constituida por un conjunto de establecimientos que pertenecen a una sola clase Clasificación
Industrial Internacional Uniforme (CIIU). Además, el establecimiento
se define como una empresa o parte de una empresa situada en un
único emplazamiento y en el que sólo realiza una actividad productiva
(no auxiliar) o en que la actividad productiva principal genera la mayor
parte de valor agregado.
4
Tomado de Naciones Unidas (2000). Manual sobre la compilación y el análisis de los
cuadros Insumo-Producto.
27
Producto: Las expresiones “productos” y “bienes y servicios” se usan
indistintamente y se clasifican conforme a la Clasificación Central de
Productos (CCP) de las Naciones Unidas al igual que en la Clasificación de Productos de Venezuela (CPV) y perfectamente vinculadas
entre sí y la CIIU.
Producción Principal: Todos aquellos bienes y servicios que son producidos dentro de un establecimiento, que están disponibles para el
empleo fuera de este mismo establecimiento, la cual le reporta la mayor parte de valor agregado y define la actividad principal del establecimiento.
Producción Secundaria: Todos aquellos bienes y servicios que son producidos en menor proporción que el producto principal o aquellos productos que se producen separados o vinculados a los productos principales dentro de una misma actividad productiva.
Producción Industrial: Es el valor total de todos los productos producidos por una industria, incluidos los primarios y secundarios.
Producción de un producto: Es el valor total de un producto producidos por todas las industrias, es decir, todos los productos residentes de
un país, producidos tanto en forma principal como secundaria.
Productor de mercado, por cuenta propia (uso final propio) y otros
productores de no mercado: En el SCN, las industrias están agrupados en estas tres grandes categorías que se describen de la siguiente
manera: un productor de mercado es un establecimiento o una empresa cuya producción se comercializa en su totalidad5. Los productores
por cuenta propia son los establecimientos cuya producción se desti-
5
Es perfectamente posible para los productores de mercado, obtener alguna producción de
no mercado destinada a su propio consumo final o a su propia formación bruta de capital.
28
na a la formación bruta de capital fijo de las empresas a las que pertenecen o bien, son aquellas empresas constituidas en sociedades de
propiedad de los hogares cuya producción se destina en su mayor parte o totalidad a consumo final o formación bruta de capital de estos
hogares ejemplo agricultores que producen para y subsistencia. Los
otros productores de no mercado son los establecimientos de propiedad de unidades del gobierno o de las Instituciones Sin Fines de Lucro
que Sirven a los Hogares (ISFLSH) que suministran bienes a precios
económicamente no significativos a los hogares o a la comunidad para
su conjunto.
Precios Básicos: Es el monto a cobrar por el productor al comprador
por unidad de un bien o un servicio producido como producto, menos
cualquier impuesto a pagar y más subvención por cobrar por esa unidad de producto como consecuencia de su producción o venta. Este
precio no incluye gastos de transporte facturados por separado por el
productor.
Precios Productor: Es el monto a cobrar por el productor del comprador por una unidad de un bien servicio producido como producto, menos el IVA (Impuesto al valor agregado) u otro impuesto deducible
análogo facturado al comprador. Este precio no incluye gastos de transporte facturados por separado por el productor.
Precios Comprador: Es la cantidad pagada por el productor del comprador, excluido cualquier IVA u otro impuesto deducible análogo, con
el fin de hacerse cargo del mismo en el momento y lugar requerido. El
precio de comprador incluye los gastos de transporte pagados por separados por el comprador.
Valoración de la Producción: Este concepto es clave en la evaluación de la consistencia de la matriz Insumo-Producto, aquí se muestra
“los bienes y servicios producidos para su venta en el mercado a precios económicamente significativos pueden valorarse a precios bási-
29
cos o a precios de productor. El método de valoración preferido es a
precios básicos, especialmente cuando funciona un sistema de IVA o
de otro impuesto deducible”6 (Naciones Unidas, 2000).
I.6 Cuadros de Oferta y Utilización (COU) y el Modelo Insumo-Producto (MIP)
Los cuadros Insumo-Producto se construyen siempre sobre la base de
ciertos supuestos analíticos, tomados normalmente de los Cuadros de
Oferta y Utilización (COU) existentes. El SCN de 1993 recomienda la
utilización de los cuadros estadísticos de oferta y utilización, que se
denominan algunas veces como cuadros Insumo-Productos rectangulares, cuadros de producción y usos, cuadros de oferta y disposición
de mercancías, etc7. (FMI, OCDE, Naciones Unidas, 1993: p. 378).
Con relación a las unidades estadísticas para el Modelo Insumo-Producto, el FMI, OCDE, Naciones Unidas (1993, p. 378), menciona que
las unidades institucionales pueden simultáneamente realizar diferentes clases de actividades productivas y recomienda que dichas unidades se repartan en establecimientos separados, cada uno dedicado a
una sola actividad productiva. “Las industrias se definen como grupos
de establecimientos dedicados a la misma actividad productiva...”, es
decir, que fuesen unidades de producción homogénea (unidad de producción que realiza una sola actividad productiva-no auxiliar), que son
la base para la elaboración de los cuadros simétricos Insumo-Producto.
Cuando un establecimiento realiza más de una actividad productiva en
relación a la clasificación dada de actividades, se tiene que distinguir
entre actividades principales y secundarias y por otro lado las actividades auxiliares. La actividad principal de un establecimiento es aquella cuyo valor agregado bruto supera a cualquier otra actividad dentro
6
Los precios de productor se pueden utilizar cuando la valoración a precios básicos sea
viable.
7
Los cuadros simétricos Insumo-Producto también reciben con frecuencia el nombre de
cuadros o matrices (Insumo-Producto) cuadrados o cuadros (matrices) Insumo-Producto
de Leontief, etc. Por otra parte, los cuadros de oferta y utilización y los cuadros InsumoProducto adoptan reglas contables del SCN, es decir, las reglas generales de tratamiento
de las transacciones.
30
de la misma unidad; la actividad secundaria es la realizada dentro de
un establecimiento además de la principal y una actividad auxiliar es la
actividad de apoyo para crear condiciones para que se puedan desarrollar las actividades de una empresa. Un establecimiento puede incluir varias actividades productivas aunque deban separarse para la
construcción de los cuadros Insumo-Producto. Las actividades auxiliares producen típicamente servicios que son usados como insumos
en casi todas las clases de actividades productivas, y el valor tiende a
ser bastante pequeño con relación a las actividades principales y secundarias a las que se halla asociada8 (FMI, OCDE, Naciones Unidas,
1993).
Por otro lado, la producción de una industria puede incluir dos o más
productos cuando éstos se obtienen simultáneamente en una sola actividad productiva bajo la forma de productos conjuntos. Los productos
conjuntos pueden distinguirse como productos principales si alcanza
la mayor proporción y por otro lado se distingue los subproductos que
se trata como productos secundarios en el marco del Insumo-Producto.
Estos aspectos son relevantes en la elaboración de las cuentas de producción al nivel primario de la información, como lo es el establecimiento, debido a que esta información se utiliza para la agregación al
nivel de las diferentes actividades y que conforman el principal insumo
al momento de consolidarlas en el COU.
I.6.1 Estructura del Cuadro de Oferta y Utilización de la economía venezolana
El cuadro de oferta y utilización que se ubica al final del Capítulo I, es
una gran matriz subdividida en 7 submatrices de información dispuestas
de la siguiente manera: las matrices A, B y C se refieren a la información de la oferta; las matrices D, E y F hacen alusión a la información
8
Las actividades auxiliares no se registran explícitamente, los insumos y el valor agregado
de estas actividades son tratados como insumos y valores agregados de las actividades
principales y secundarias, respectivamente.
31
de demanda; y las matrices G y H contienen información adicional de
interés, que incorpora nuevos elementos analíticos.
Por el lado de las filas, se dispone de la misma información que está
contenida en cada cuenta de producción que se realiza desde el nivel
estadístico primario, el establecimiento, hasta llegar a un nivel de agregación por actividades económicas consolidado en el presente cuadro.
Esta estructura contiene principalmente la desagregación tanto de la
producción como del consumo intermedio al nivel de 300 productos.
Así mismo, se dispone del valor agregado y de sus componentes. Adicionalmente, se dispone de información de la formación bruta de capital fijo, la variación de existencias, el personal ocupado y algunas
líneas de totalizaciones y ajustes.
Por el lado de las columnas, se disponen los diferentes componentes
de la oferta y de la demanda. El primero dispone de la producción
nacional abierta por actividades y clasificadas entre actividades de
mercado, no mercado y uso final propio. Adicionalmente, se dispone
de las importaciones y del resto de componentes de oferta para llevar
la misma desde los precios básicos a precios de comprador. Por el lado
de la demanda, la misma está compuesta por el consumo intermedio,
consumo final de los hogares, consumo privado no lucrativo, consumo
del gobierno, abierto en consumo colectivo e individual, formación
bruta de capital fijo, variación de existencias y adquisición menos disposiciones de objetos valiosos, para así llegar al total de la demanda la
cual se iguala a la oferta a precios de comprador.
El cuadro de oferta
Las tres primeras submatrices conforman la oferta total de la economía, donde la submatriz B dispone de la información de producción de
cada actividad, clasificadas estas en actividades de mercado, no mercado y uso final propio, abiertas por productos y representando toda la
desagregación de la producción nacional, valorada a precios básicos.
32
Es así como cada actividad dispone de los productos que produce en
forma principal o secundaria, como también si la producción de los
mismos es de mercado, no mercado o uso final propio. Adicionalmente, la submatriz C dispone de las importaciones abiertas por productos, valoradas CIF. Luego la matriz A dispone del resto de información
para llevar la valoración de precios básicos a precios de comprador
agregándole a las dos submatrices previas a la información de los derechos de importación, los impuestos y subvenciones a los productos,
IVA y los márgenes de distribución.
El cuadro de utilización
Las submatrices D, E y F componen la desagregación de todos los
componentes de la demanda, disponiendo en la primera del consumo
intermedio utilizado por cada actividad en su proceso productivo,
desagregándolo igualmente en las actividades de mercado, no mercado
y uso final propio, así como su respectiva apertura en los 300 productos medidos a precios de comprador, que es el precio que el demandante tiene que pagar por la unidad de producción. Esta matriz viene a
ser el principal insumo del MIP. Adicionalmente se dispone de la
submatriz E, la cual desagrega las exportaciones, valoradas FOB. Por
último, la submatriz F dispone del resto de los componentes de demanda, valorados a precios de comprador, los cuales corresponderían a ser
las variables exógenas dentro de MIP desarrollado en este trabajo.
Información adicional por actividad
El COU permite disponer adicionalmente de la información de oferta y
demanda, información desagregada por actividades económicas tanto
del valor agregado de cada una de ellas como de los diferentes componentes del mismo como son: las remuneraciones, otros impuestos y
subvenciones a la producción, excedente de explotación e ingreso mixto,
dispuestos en la submatriz G. Por último, la submatriz H incorpora
información adicional propia de cada actividad que permite realizar
33
otra serie de análisis de interés sobre la misma, como es la información
de la formación bruta de capital fijo demandada por la actividad, la
variación de existencias y el personal ocupado que es requerido por
cada actividad económica en su proceso productivo.
Algunos ajustes de interés9
Son varios los ajustes necesarios a realizar en el COU, sin embargo,
sólo se mencionan cuatro que se consideran de importancia explicarlos. El primero está referido al ajuste CIF-FOB, el cual consiste en
incorporar a las importaciones al nivel de los productos, las cuales
están valoradas CIF, la información referida a los servicios de transporte prestados por transportistas y los seguros prestados por aseguradores residentes y no residentes. Esto con el objeto de disponer el
nivel total de las importaciones valoradas FOB y poder ser consistentes y estar armonizados con el nivel de importaciones del sistema de
Balanza de Pagos.
El segundo ajuste está referido al ajuste de los márgenes comerciales y
de transporte, en donde los servicios comerciales que se incluyen en el
grupo de servicios de mercado y que se consumen por los productores
y usuarios finales, no comprende los márgenes comerciales de transporte, que sí poseen el valor de los bienes a precios de comprador. En
consecuencia, por el lado de la oferta debe deducirse de la oferta total
de servicios.
El tercer ajuste corresponde al ajuste a las compras de los residentes
en el extranjero las cuales según el manual del SCN 1993, se tratan
como importaciones y como gasto final de los hogares, suponiendo
que sólo la realizan los residentes de los hogares. Por consiguiente,
debe incorporarse el ajuste de los gastos de viajeros de negocios que
se tratan como consumo intermedio y el gasto de hogares que se trata
9
Tomado de Naciones Unidas (2000). Manual sobre la compilación y el análisis de los
cuadros Insumo-Producto.
34
como consumo final de hogares en las importaciones del cuadro de
oferta y en el gasto final de hogares del cuadro de utilización, respectivamente.
Por último, el ajuste a las compras de no residentes en el país según el
cual deben tratarse como exportaciones, por consiguiente, debe en el
gasto final de hogares del cuadro de utilización, respectivamente. Al
igual que las compras en el extranjero por parte de los residentes, se
recomienda la clasificación de las compras realizadas por no residentes se puedan obtener por producto y que se hagan directamente en el
vector de gasto final de hogares.
En atención a lo expuesto en este capítulo, la integración del Modelo
Insumo-Producto con los nuevos enfoques del Sistema Cuentas Nacionales de 1993, constituye una de las bases principales para la observación de la estructura de la economía venezolana, por otro lado,
permite ampliar la información para el análisis estadístico-económico,
apoyo al mejoramiento en las mediciones de los agregados macroeconómicos. En sentido, no hay que negar que el Programa de Actualización
de las Estimaciones Macroeconómicas (Pracem) constituye de una
manera armónica y articulada un gran paso a la actualización y modernización de las estadísticas económicas, cuyo dominio está definido
en comprender el movimiento de los sistemas estadísticos integrado
desde la información de la unidad económica primaria (establecimiento)
hasta el proceso de interconexión, compatibilización y armonización de
los resultados en forma agregada.
35
El cuadro de oferta y utilización10
10
Tomado del Sistema de Cuentas Nacionales y elaboración propia.
36
II.
EL MODELO INSUMO-PRODUCTO (MIP)
COMO INSTRUMENTO DE ANÁLISIS ECONÓMICO
Este capítulo busca mostrar una visión general del Modelo InsumoProducto como instrumento de análisis económico, haciendo énfasis
en su utilidad y en la importancia de la confiabilidad de los coeficientes utilizados, la cual justifica que se proyecte el interés de estudiarlo.
En este mismo orden de ideas, se hace mención a los usos y limitaciones, derivados del modelo, en función de proporcionar un acercamiento
cualitativo de los márgenes de error incorporados al evaluar los resultados provenientes del análisis Insumo-Producto.
Por otro lado, se expondrán algunos aspectos relevantes sobre experiencias en la construcción y análisis del Modelo Insumo-Producto, las
cuales se consideraron importantes dilucidar, debido a sus aportes e
incidencias en el planteamiento de nuevos problemas y en la explicación de nuevos fenómenos vinculados con las relaciones intersectoriales.
De igual manera, se mostrarán algunas consideraciones del MIP, como
base analítica y teórica en el inicio de otras investigaciones, con la
finalidad de abrir espacios en la discusión sobre la importancia de estos modelos multisectoriales en el análisis económico.
II.1 Visión general del MIP
La Matriz Insumo-Producto, es un registro ordenado de las transacciones entre los sectores productivos orientadas a la satisfacción de bienes
para la demanda final, así como la compra y venta de bienes intermedios; en este sentido, es importante tener presente que es indispensable
en el análisis de las relaciones interindustriales, para el estudio de una
serie de problemas empíricos a partir de las relaciones Insumo-Producto,
en la cual resultan inadecuadas otras técnicas o instrumentos de carácter más agregado.
37
Según el Banco Central de Chile (1996, p. 12) las matrices InsumoProducto son:
Una representación simplificada de la economía que muestra la estructura de la generación y uso de la oferta de bienes
y servicios, para un período seleccionado que se define como
año base. Ello se expresa mediante un conjunto de tablas de
doble entrada, donde la producción obtenida por las distintas actividades económicas se registra en las filas de las tablas y su respectivo uso intermedio o final, en las columnas.
Por uso final de la producción se entiende el consumo, la
inversión y las exportaciones.
El modelo de Insumo-Producto es un método eminentemente cuantitativo, que permite el análisis objetivo de un sistema económico; por
otro lado, enlaza el análisis microeconómico de corte neoclásico como
instrumento operativo de la teoría del equilibrio general con la teoría
macroeconómica keynesiana, y su estructura implica la existencia de
unidades intermedias de análisis, entre las empresas individuales y los
agregados macroeconómicos, suficientemente agregados para permitir la comparación internacional y suficientemente desagregado que
permita inferir acerca de comportamiento más probable de agentes individuales. El estudio de estas unidades de análisis se ha dado en llamar mesoeconomía y su herramienta más poderosa es el modelo de
Insumo-Producto (Laguna, 2003).
La técnica de Insumo-Producto se debe a Wassily Leontief en 1941, y
fue construida inicialmente para el análisis nacional de las modificaciones estructurales de la economía norteamericana, debido a sus múltiples posibilidades de uso práctico en el análisis económico, en la
formulación de políticas y en la realización de pronósticos. Por consiguiente, el análisis interindustrial se orienta al examen cuantitativo de
las interacciones entre los agentes productivos, dado su carácter de
consumidores y proveedores de recursos.
38
La interpretación de la estructura económica constituye uno de los principales usos del modelo, lo cual permite determinar la consistencia
interna de los planes de desarrollo y detectar las fallas en el sistema.
De igual manera, el modelo tiene aplicaciones para la investigación y
el análisis de los cambios estructurales de una economía; permitiendo
medir cambios en la productividad, estudiar las repercusiones de una
sustitución de recursos y determinar el impacto de las variaciones en el
valor de los insumos sobre la estructura de costos, lo que en conjunto
permite tener nociones de los avances tecnológicos operados en la
economía, (Laguna, 2003).
En este mismo orden de ideas, el Banco Central de Chile (1996,
p. 12) manifiesta que es necesario elaborar matrices de Insumo-Producto para actualizar en un esquema coherente e integrado, las distintas
variables macroeconómicas del sector real. Además, este instrumento
permite determinar principalmente los distintos flujos que constituyen
la oferta y demanda de bienes y servicios, actualizar las funciones de
producción, posibilitando el mejoramiento de las mediciones del PIB
por actividad económica y de las variables que componen el gasto,
ahorro e inversión.
Por otra parte, cabe destacar que la construcción de una MIP permite
determinar los impactos de los choques tecnológicos que afectan a la
producción, variaciones en las formas de consumo, aparición y desaparición de productos, cambios en la forma de organización de los
mercados y la ejecución de determinados regímenes de política económica. Estos fenómenos repercuten en el nivel y relación de precios en
la economía nacional, alterando el patrón de medida de la actividad
económica derivado del año base seleccionado. Mientras más se aleja
la medición de cuentas nacionales de dicho año base, la validez del
cálculo a precios constantes se deteriora progresivamente. Visto de
esta forma, genera la posibilidad de dar continuidad a nuevas matrices
Insumo-Producto que permita hacer valoraciones del comportamiento
del producto, gasto e ingreso de la economía con precios más cercanos
a los vigentes durante los períodos de medición de estas variables (Banco
Central de Chile, 1996).
39
Para Laguna (2003), la utilidad del modelo de Insumo-Producto depende de la confiabilidad de los coeficientes utilizados, los cuales se
deducen de las transacciones totales y se proyectan para el año de
interés; lo que implica una serie de dificultades derivadas de los
supuestos bajo los que opera el modelo. En primer lugar, la consideración de un cambio tecnológico nulo no es del todo correcta para ciertos
sectores, además, es evidente que el supuesto de que sólo existe un
único proceso de producción para cada sector no se cumple del todo.
Otra dificultad radica en el nivel de agregación que se use en el análisis, ya que una adecuada planificación normalmente requiere un nivel
de desagregación que resulta difícil de operar para los tomadores de
decisiones.
Por su parte, en el modelo dinámico la limitación radica en la dificultad para realizar estimaciones fiables de la matriz de coeficientes de
capital, así como la dificultad para asegurar la viabilidad, derivada de
la posibilidad de niveles de inversión negativos.
II.2 Usos y limitaciones del Modelo Insumo-Producto
Exponer de manera general los usos y limitaciones de este modelo,
permite dar una idea cualitativa de los márgenes de error, incorporados
al analizar los resultados, exponer conclusiones y proponer recomendaciones, con relación a las posibles interpretaciones de los movimientos
e interrelaciones de los sectores productivos, que se orientan a la producción de bienes y servicios, y a la satisfacción de una demanda final
que se supone exógena.
II.2.1 Usos
Así como el MIP permite medir los impactos directos e indirectos en la
producción como consecuencias de la demanda final, es importante
evaluar, que las decisiones concernientes a variaciones del empleo en
una actividad, repercutirá en sí misma, así como en todos los sectores
vinculados a ella, de aquí que el efecto completo en los requerimientos
40
de empleo directos e indirectos se puede cuantificar sólo en una matriz
con las características que describe el modelo Insumo-Producto.
En este sentido, el Instituto Nacional de Estadísticas y Censos de Argentina (1997, p.1), señala que:
Para el empresario, que conoce bien el sector de la actividad
en donde están ubicados los compradores de los bienes y
servicios que produce, pero que conoce menos sobre la rama
de actividad de los clientes de sus compradores, el MIP ofrece
un detallado análisis de la ruta que siguen los bienes y servicios hasta llegar a la demanda final; y le brinda la participación relativa a la empresa en el total de una determinada
rama de actividad con sus consecuentes posibilidades de expansión en el mercado.
Por otro lado, Antonelli y Lorente (1997) mencionan que el uso de las
matrices Insumo-Producto pueden extrapolarse en el análisis de las
importaciones y exportaciones, con la ayuda de alguna información
complementaria para el cálculo de la balanza comercial como consecuencia del enfoque intersectorial seguido por el MIP. Para el Banco
Central de Chile (1996), Naciones Unidas (2000) y el Instituto Nacional
de Estadística y Censos de Argentina (2001) coinciden, que el desarrollo y mantenimiento de los Modelo Insumo-Producto, permite la
actualización de las funciones de producción tanto sectorial como
agregada de una economía, posibilitando el mejoramiento de las mediciones del PIB y de las interrelaciones entre los sectores productivos.
De igual manera, si se dispone de información corriente, constante y
de precios, se puede determinar como los impactos de los choques
tecnológicos que afectan a la producción, aparición y desaparición de
productos, la evaluación de determinados regímenes de política económica y de igual manera determinar el patrón de medida para determinar e implantar un nuevo año base.
41
En muchas investigaciones, se ha tenido que desempolvar el instrumento estadístico desarrollado por Wassily Leontief en la década del
30: la matriz Insumo-Producto, para intentar comprender lo que está
pasando en el presente y su devenir futuro, ejemplo de ello es Ascúa
(2001), que observa cuáles son las repercusiones que trae el abandono
de los sistemas de convertibilidad de la moneda que conduce
automáticamente a pensar en ganancias automáticas de competitividad internacional en aquellos sectores menos expuestos al efecto de
insumos y materias primas originados en importaciones.
El Banco Central de la República Argentina (BCRA) (1997), expone,
que así como el MIP permite medir los impactos directos e indirectos
en la producción como consecuencia de cambios en la demanda final,
lo mismo puede decirse con respecto a las decisiones tendientes a
reducir el desempleo, las cuales pueden llegar a tener una base estadística más sólida: por ejemplo, la expansión de la actividad de la construcción, repercutirá en la actividad en sí misma, así como en todos los
sectores vinculados a ella, de aquí que el efecto completo en los requerimientos de empleo directos e indirectos se pueda cuantificar a partir
de un modelo Insumo-Producto. Por consiguiente, García y Amo Saus
(2000), señalan, que para modelizar los flujos de bienes y servicios
recogidos en una matriz Insumo-Producto y dar una interpretación más
completa acerca del grado de integración de una rama en toda la estructura de producción, introducimos una relación llamada relación de
influencia, es decir, que al variar la producción en la rama productiva
i influye en la producción de la rama productiva j.
Esta definición puede centrarse en términos relativos, puesto que las
variaciones relativas suelen ser a menudo más útiles que las absolutas,
esto permite observar la interrelación intersectorial del modelo InsumoProducto. Por tanto, la influencia directa relativa de la rama i sobre la
rama j, denotada por i es el incremento relativo en la producción de
la rama j cuando se produce un aumento relativo de la producción de la
rama i, es decir,
i JD ⇒ j =
ΔXj / Xj
ΔXi / Xi
42
Si van en la misma dirección es positiva, si van en direcciones contrarias es negativa y si no ejerce influencia es nula.
En este mismo orden de ideas, Long y Plosser (1983), argumentan que
una importante característica observada en los ciclos económicos, es
la tendencia que tienen de los productos a moverse juntos en diferentes sectores. Este análisis de los comovimientos entre varios sectores
es necesario, para investigar las propiedades del sistema como un todo;
en la cual, la matriz de costos de Modelo Insumo-Producto, permite
bajo la observación de sus propiedades estocásticas y la obtención
matriz de una de autocovarianza, simular la conducta, la interdependencia o dependencias intersectorial ante shocks internos sobre coeficiente
técnico {aij} como costo del insumo j en la producción del producto i.
Por otro lado, Ambler, Cardia y Zimmermann (2000), analizan la transmisión internacional de los ciclos económicos en modelos multisectoriales y los efectos relativos sobre múltiples sectores.
El análisis Insumo-Producto nos permite estudiar los cambios estructurales en la economía (Planning, 2000), proporcionando, una herramienta necesaria para evaluar las industrias, extendiendo el análisis
para el estudio de sectores, actividades y productos, incluyendo sus
relaciones sobre el resto de la economía y el efecto sobre las relaciones internacionales de dichas relaciones. Según Baumol (2000), este
ha sido una de las mayores contribuciones a la economía en el siglo
XX11. Es así, como el MIP constituye una herramienta central en el
análisis económico, ya que permite indagar las repercusiones sectoriales frente a variaciones que son consecuencia de las decisiones de los
particulares o de los responsables de la definición de la política económica y de igual manera, Císcar (1998), menciona que los MIP son
usados para reportar y cuantificar los efectos socioeconómicos de los
proyectos de energía renovable, para el caso de los países del Mediterráneo y las tabla Insumo-Producto usadas son de Turquía, Tunisia y
Marruecos.
11
The mutual support that theory, data and application have come to provide to one another.
43
Es importante mencionar, que todo cambio en el producto obedece
principalmente a patrones de demanda y cambios tecnológicos y de
igual manera estos cambios en la producción afectan los salarios y el
empleo; es por ello que Rozenov (1998), hace uso de las tablas InsumoProducto y su interconexión con la actividad económica, para analizar
las características estructurales12 de la economía de Bulgaria, altamente vinculada con alta inflación y volatilidad en las tasas de interés.
Finalmente, resulta claro que uno de los aspectos fundamentales e importantes que posibilita el conocimiento con profundidad de una economía es la realización de un análisis de su estructura productiva.
Dicho análisis supone una importante ayuda no sólo en la evaluación y
en la toma de decisiones de política económica, sino también constituye un requisito indispensable en las decisiones de crecimiento empresarial. En este sentido, el estudio de una economía puede abordarse
desde muy diversas ópticas, una de las cuales es el enfoque InsumoProducto, el cual permite analizar conjuntamente las relaciones
intersectoriales de una economía y su demanda agregada, con lo cual
se dispone de un conocimiento integrado de la actividad económica.
II.2.2 Limitaciones
Las limitaciones del Modelo Insumo-Producto, están relacionadas principalmente con la rigidez de los supuestos sobre el cual se basa el
modelo, de allí pues, que el abordaje de los resultados sobre el estudio
del circuito económico se realicen desde muy diversas perspectivas,
de esta forma, las restricciones impiden analizar instantáneamente las
relaciones intersectoriales, y en algunos casos es necesario flexibilizar
muchos de los supuestos para disponer de una visión integral del comportamiento de una o varias actividades económicas en la generación
de bienes y servicios.
12
Guo y Planning (2000), también usan los análisis Insumo-Producto para observar los
cambios estructurales de una economía.
44
Uno de los aspectos determinantes que impide el análisis instantáneo
de las relaciones Insumo-Producto, es la presencia de producción secundaria en las actividades productoras de bienes y servicios, caso
normal en cualquier economía; pero en este sentido, al trabajarse en el
modelo directamente y sin establecer técnicas para resolverlos los productos secundarios, los coeficientes deducidos y descritos en la matriz
inversa serán espurios o distorsionados. Venegas citado por (Banco
Central de Chile, 1996).
Por otro lado, Banco Central de Chile (1996) y Chiang (1997), destacan que el Modelo Insumo-Producto (Leontief) busca responder, cual
es el nivel de producción que debe alcanzar las n-industrias de una
economía para satisfacer una demanda final, dados unos supuestos
básicos, visto de esta forma, el MIP se transforma en una herramienta
de gran utilidad en la planificación de la producción; pero sí se simplifica el análisis, los supuestos teóricos que pueden limitar el desarrollo
del Insumo-Producto son:
1
La Homogeneidad: esta exige que todos los productos de un sector se produzcan en proporciones fijas y sin sustitución automática
de productos, en la cual, cada industria produce un bien homogéneo (no admite productos secundarios).
2
Cada industria usa una relación fija de insumos o combinación de
factores para alcanzar su producto, está asociado al supuesto de
la Proporcionalidad, es decir, los insumos de un sector varían en
proporción directa a las variaciones de su producción total (Rendimientos Constantes a Escala). Por otro lado, se asume inicialmente que los precios de los factores y los productos están dados.
3
La Aditividad: El efecto total de la producción en varios sectores
es igual a la sumatoria de diferentes efectos.
45
4
Limitaciones del Análisis Estático, como punto fundamental el
MIP ignora el proceso real de ajuste y reajustes de las variables
que finalmente conducen al estado de equilibrio. El tipo de análisis estático falla a tener en cuenta a dos importantes problemas:
1) El ajuste puede requerir bastante tiempo hasta completarse,
entonces, puede tener relevancia incluso antes de alcanzarse, si
mientras tanto las fuerzas exógenas al modelo experimentan ciertos cambios (problemas de cambio en el estado de equilibrio). 2)
Aun cuando el proceso de ajuste contiene su curso sin ser perturbado, no se puede alcanzar en su conjunto el estado de equilibrio
concebido en un análisis estático (problema de equilibrio inestable), en donde, el proceso de ajuste se alejaría de las variables de
su estado de equilibrio, en lugar de acercarlas progresivamente.
Los cambios en el estado de equilibrio (como respuesta a cambios exógenos) pertenecen a un análisis de estática comparativa
la cuestión de accesibilidad y la estabilidad del equilibrio cae
dentro del análisis dinámico.
En este mismo orden de ideas, Quan Kiu (2001, p.151), recalca que es
sumamente importante no olvidar las limitaciones que presenta el modelo, las cuales se deben de tomar en cuenta para corregir estimaciones y desviaciones en la medida de lo posible. Bajo esta premisa, las
dos principales limitaciones que se presentan son: a) la linealidad, que
es la que considera que los coeficientes son idénticos a cualquier nivel
de producción sin tomar en cuenta las economías de escala, y b) la
estática tecnológica que no toma en cuenta la velocidad con que en la
actualidad cambia la tecnología, es decir, el MIP asume la no existencia de choques tecnológicos persistentes que modifiquen los coeficientes
técnicos asumidos fijos.
Finalmente, el Instituto Nacional de Estadística e Informática del Perú
(2001), coincide con que los superávit o excesos en la producción, que
no son absorbidos en el mismo proceso productivo son adquiridos en
el Modelo Insumo-Producto como demanda final, por lo tanto, restringe los análisis y resultados, desde la perspectiva en la cual el estado de
equilibrio concebido en un análisis estático, es un equilibrio contable
46
de oferta total igual a la demanda total y este sentido no se consideran
las variaciones de los precios como mecanismo de vaciado de los marcados.
II.3 Aspectos relevantes de experiencias en Insumo-Producto
En esta parte, se mencionarán casos generales y relevantes de los procesos de aplicación y presentación del Modelo Insumo-Producto, las
cuales se consideran necesarias para el abordaje y estudio del circuito
económico en el cual fluyen las relaciones intersectoriales, en el sentido de disponer de un conocimiento integrado de la actividad económica. Entre los aspectos relevantes a mencionar se tiene: la matriz InsumoProducto para Venezuela desarrollada por Clemente y Puente (1989),
la Matriz Insumo-Producto del Caribe colombiano y un análisis InsumoProducto de la economía balear.
II.3.1 La Matriz Insumo-Producto para Venezuela (1981 y 1984)
La matriz Insumo-Producto del año 1981 y 1984 desarrollada por Clemente y Puente (1989), es un aporte importante en la evaluación de las
estructuras productivas y en el análisis intersectorial de la economía
venezolana; por consiguiente, muestra una serie de consideraciones
generales acerca de la potencialidad del Modelo Insumo-Producto en
la determinación de los sectores encadenantes o dinamizadores del
proceso producido, que abarca la producción y generación de bienes y
servicios.
En este sentido, Clemente y Puente (1989, p. 78) plantearon la necesidad de evaluar la evolución de la estructura sectorial de la economía
venezolana entre 1981 y 1984 con base en las matrices Insumo-Producto, a través de un conjunto de multiplicadores que permiten considerar la jerarquía sectorial. Sin embargo, la confiabilidad del análisis
Insumo-Producto está relacionada con el volumen de información directa que es posible obtener respecto a cada uno de los cuadrantes que
configuran la matriz, particularmente los insumos intermedios o tran-
47
sacciones intersectoriales; por otro lado, la potencialidad de este instrumento en el análisis multisectorial es una gran base para la planificación a nivel sectorial y macroeconómica, al permitir presentar una
estructura coherente y amplia de las relaciones técnicas entre los sectores o actividades productivas y por consiguiente, se puede comprobar la validez de los agregados macroeconómicos.
Según Clemente y Puente (1989, p. 100) “los análisis intersectoriales
han sido una constante para identificar una jerarquía de sectores según
la capacidad de los mismos para inducir efectos multiplicadores sobre
el sistema económico”. En estos análisis juegan un papel importante
las características de los enlaces o encadenamientos intersectoriales.
Para ello, es necesario estudiar adecuadamente los enlaces
intersectoriales y sus efectos sobre la economía en su conjunto, analizando los sectores desde una doble jerarquía:
1
La jerarquía de “oferta”, se fundamenta en las desigualdades de
la capacidad de transmisión que tienen los distintos sectores de la
economía según su estructura productiva, entendiendo por ello el
efecto que ejerce la variación de la demanda de un sector en el
resto de los sectores y depende de la estructura de costos sectoriales, las importaciones y la elasticidad de la inversión sectorial
respecto a los incrementos de la demanda.
2
La jerarquía de “demanda”, está fundamentada en la parte del
ingreso que es destinado a la compra de los distintos bienes finales. Este efecto sobre la producción, es inducido por el ingreso y
denominado por algunos autores como capacidad de absorción.
Por otro lado, se introduce la dimensión del mercado en el análisis que depende de la relación existente entre el ingreso y la demanda.
En resumidas cuentas, el MIP debe estar orientado a resaltar el carácter encadenador de un sector (o de un conjunto de sectores) la cual
48
depende de su evaluación, su transmisión y efecto combinado de la
capacidad de absorción.
II.3.1.1 Análisis de la capacidad de encadenamiento
Al realizar estudios sobre la estructura económica desde la doble perspectiva de la capacidad de transmisión y de absorción, se puede determinar que los sectores encadenantes son aquellos que ocupan los lugares
tanto en la jerarquía de transmisión como en la jerarquía de absorción.
El efecto de absorción es conveniente tener presente que este concepto
sólo es estrictamente aplicable a aquellos sectores que producen bienes de consumo final. En los sectores que producen bienes intermedios, la capacidad de absorción es indirecta, en el sentido de que el
tamaño de su mercado o su efecto depende de los sectores que ellos
abastecen. Por consiguiente; Clemente y Puente (1999, p. 102) consideran “el encadenamiento intersectorial, fundamentalmente desde el
punto de vista de la oferta o de la capacidad de transmisión”. Por lo
general, no se considera el efecto absorción, ya que la demanda de
bienes y servicios finales se presenta como un elemento exógeno o
cuando se endogeniza parte de ella tiende a considerársele en forma
similar a los flujos intermedios de bienes; para lo cual, en cierta forma
viola las características de comportamiento tanto de los ingresos como
de la demanda.
En este sentido, si se define para cada sector un vector de coeficientes
técnicos (aij) que describe la estructura productiva de compras intermedias y se supone que tiene un cierto grado de estabilidad a medida
que no existan choques tecnológicos que cambien la relación InsumoProducto.
a1j = x1j/xj
donde 0 < aij < 1 (i, j = 1, 2,…,n)
a2j = x2j/xj
anj = xnj/xj
49
El coeficiente técnico aij es el valor del bien i consumido por unidad de
producto del bien j, y su análisis privilegian medir la fuerza de los
enlaces o dar importancia al número de enlaces, por lo tanto, en ambos
enfoques la capacidad de transmisión sectorial se evalúa por los enlaces directos de los sectores.
Para medir la fuerza de los enlaces, H. Chenery y T. Watanabe citado
por Clemente y Puente (1999, p. 102) utilizan dos índices, Uj y Wi, el
primero en el sentido de las compras de insumos y el segundo, en el
sentido de las ventas. En términos más concretos:
(a) uj: Es un índice por sector donde se indica la proporción de
insumos intermedios nacionales sobre la producción sectorial, esto es,
el monto que dedica cada sector a la compra de bienes intermedios por
unidad de producción: la suma de la columna de los coeficientes técnicos de cada sector;
u j = ∑ i aij = ∑ i xij / x j Absorción (compras)
(b) wi: Este segundo índice sectorial indica la proporción de ventas intermedias respecto a la producción total del sector: la suma de la
fila de los coeficientes técnicos de cada sector:
(c)
wi = ∑i aij = ∑j .xij / x j Ventas
Para medir la fuerza de los enlaces directos se utilizan los índices
uj y wi (i=j) clasificando los sectores por orden uj decreciente y
uj creciente.
El segundo tipo de enfoque según Clemente y Puente (1999), se orienta a ordenar la capacidad de transmisión por el número de enlaces
intersectoriales, para aprovechar las características empíricas de las
50
relaciones tecnológicas intersectoriales, donde un número alto de estudios sugiere que las matrices de coeficientes técnicos tienen un número importante de enlaces nulos y por tanto pueden ser transformados
por permutación de filas y columnas en matrices triangulares. Dentro
de este marco, una matriz de coeficientes técnicos triangulares o triangular inferior es aquella donde los valores de los coeficientes son cero
por encima de la diagonal. En estas circunstancias, el sector i vende
insumos intermedios al sector j, siendo i=j; y el sector j no vende al
sector i13.
Uno de los problemas importantes de la triangulación de la matriz de
coeficientes técnicos, es la subestimación implícita que realiza este
método de la fuerza de los enlaces intersectoriales. A primera vista,
podría pensarse en que quizás sería adecuado utilizar un índice que
mida la fuerza de los enlaces, como el Uj y así evaluar la capacidad de
transmisión. Sin embargo el problema de este tipo de índice es que
privilegia los enlaces directos y en consecuencia no toma en cuenta los
efectos intersectoriales indirectos para evaluar la capacidad de transmisión.
Si por ejemplo un sector j tiene un índice Uj muy elevado, pero el
número de sus enlaces es bajo, es posible que los índices Uk, Uj, Um, de
los sectores que proveen de insumos al sector j sean bajos y por tanto
la capacidad de transmisión global del sector sea baja. Es decir, que
resulta indispensable tomar en cuenta los efectos tanto directos como
indirectos para estar en condiciones de poder evaluar satisfactoriamente la capacidad de transmisión.
Leontief (1966), menciona que el problema de las relaciones directas e
indirectas que tienen los distintos sectores es resuelto por el llamado
multiplicador matricial de Leontief, el cual en numerosos estudios se
13
Para un análisis más detallado de las implicaciones que las matrices triangulares tiene
sobre este tipo de análisis se sugiere, Palacios, L. C. (1985).
51
ha considerado como el instrumento privilegiado para evaluar el encadenamiento de la economía.
Por lo general, el multiplicador matricial se emplea suponiendo un
impulso exógeno de la Demanda Final (D), a un determinado sector, y
sobre la base del modelo estático de Insumo-Producto se determina el
aumento de la producción nacional global ΔXi.
ΔX = [I - A] -1 .ΔD
En términos más específicos la suma de cada columna j del multiplicador
matricial se puede interpretar como el crecimiento global de la producción inducida por el crecimiento unitario de la Demanda Final de ese
sector.
Leontief (1966) manifiesta que el multiplicador tecnológico de Leontief
representa un fenómeno de multiplicación amortiguada que es condicionada por la propiedad de ∑i, .aij <1 ya que sólo se toma en cuenta
las relaciones tecnológicas del capital circulante, el fenómeno de la
convergencia no depende de los rendimientos constantes (coeficientes
aij constantes), sino del hecho que se mantiene el carácter productivo
de la matriz de consumo intermedio (∑i, .aij <1, j). Si aparecen rendimientos decrecientes (o crecientes) el efecto será retardar o acelerar el
fenómeno de convergencia.
Índice de integración vertical o encadenamiento hacia atrás
Tomando como base de análisis el multiplicador tecnológico de Leontief,
Lantner y Rasmussen citado por Clemente y Puente (1989, p. 107)
sugieren dos índices para evaluar la capacidad de transmisión. Considerando a Zoj como la suma de la columna j de la matriz inversa de
Leontief [I-A]-1, es decir:
52
Si [I-A]-1 = B, entonces:
Zoj = ∑n bij,
i=1
Por otro lado, se define el índice Uoj de la manera siguiente:
U oj =
Z oj
1 / n ∑ j Z oj
El índice Uoj pretende cuantificar la fuerza de transmisión del sector j
al variar su demanda final sobre el resto de los sectores, al dividir el
valor de la suma de la columna j del multiplicador de Leontief entre
el promedio de todos los sectores. Si el índice Uoj es mayor que la
unidad (>1), quiere decir que este sector tiene mayor capacidad de
encadenamiento y viceversa si Uoj es menor que la unidad (<1).
Sin embargo, aun cuando Uoj (>1) resulte mayor que la unidad, el sector j puede encadenar pocos sectores, por lo tanto, se requiere de un
índice que permita conocer la dispersión de la distribución del encadenamiento. El índice que permite analizar esta situación se denomina Voj.
Voj se define así:
1
1
n
∑ (bij − ∑ bij ) 2
n − 1 i =1
n i =1
Vij =
1
∑ bij
n i =1
1/ 2
Mientras más bajo sea este índice mejor encadenado o integrado estará el sector j, ya que la dispersión de cada coeficiente con respecto a la
media será menor. En definitiva, combinando estos tres índices
(Zoj, Uoj y Voj) es posible afirmar que un sector j estará más integrado
verticalmente si Zoj y Uoj tienen valores mayores que la unidad, es decir, si el sector j ejerce una influencia cuantitativa relevante sobre la
53
estructura económica; y además, si el índice Voj es bajo, es decir, que la
influencia ejercida por el sector j está distribuida hacia un amplio número de sectores en la economía.
Índice de integración horizontal o encadenamiento hacia delante
Este índice intenta evaluar el efecto que sobre la producción sectorial
tiene el aumento en la demanda final de una unidad en todos los sectores, es decir, del total de la producción generada por este aumento en
la demanda, nos indica en cuanto participó directamente el sector considerado.
En el sistema de Insumo-Producto, la integración horizontal queda definida por la suma por fila de los coeficientes de la matriz de requisitos
directos e indirectos, es decir, la matriz [I - A]-1.
Zio = ∑n bij,
i=1
Por otro lado, se define el índice Uio de la manera siguiente:
U io =
Z io
1 / n ∑ i Z io
El índice Uio pretende cuantificar el efecto que sobre la producción
sectorial que tiene el aumento de demanda final de una unidad en todos los sectores; el efecto sobre el sector i se obtiene al dividir el valor
de la suma de la fila i del multiplicador de Leontief entre el promedio
de todos los sectores. Si el índice Uio es mayor que la unidad (>1),
quiere decir que este sector tiene mayor capacidad de encadenamiento
hacia adelante y viceversa si Uio es menor que la unidad (<1).
Por otro lado, aun cuando Uio (>1) resulte mayor que la unidad, el
sector i puede encadenar pocos sectores, por lo tanto, se requiere de
54
un índice que permita conocer la dispersión de la distribución del encadenamiento hacia adelante. El índice que permite analizar esta situación se denomina Vio
Voj se define así:
1
1
n
∑ (bij − ∑ bij ) 2
n − 1 j =1
n j =1
Vio =
1
∑ bij
n j =1
1/ 2
Mientras más bajo sea este índice mejor encadenado o integrado estará el sector j, ya que la dispersión de cada coeficiente con respecto a la
media será menor. En definitiva, combinando estos tres índices (Zio,
Uio y Vio) es posible afirmar que un sector j estará más integrado horizontalmente, si Zio y Uio tienen valores mayores que la unidad, es decir,
el aumento en una unidad en la demanda final del resto de los sectores
ejerce una gran influencia sobre la producción sectorial el sector i; y
además, si el índice Vio es bajo, es decir, que la influencia ejercida a la
producción del sector j está concentrada en un amplio número de sectores en la economía.
Una metodología similar ha sido propuesta por Mougeot, Duru y Aury
citado por Clemente y Puente (1999, p. 109), pero desde la perspectiva de las ventas que realiza cada sector, en la cual, a pesar de las
diferencias existentes entre el multiplicador tecnológico de Leontief y
el de Mougeot, Duru y Aury, el primero define una estructura en función de las compras y el segundo en función de las ventas, en términos
generales ambos enfoques establecen los sectores claves o integrados
dentro de la estructura productiva existente.
También García y Ramos (2003), concuerdan que a pesar de las limitaciones del uso de estos índices, mencionan que existe un consenso
generalizado sobre el adecuado comportamiento de los coeficientes
55
clásicos de Chenery y Watanabe, Rasmussen o Streit, utilizados para
el análisis y estudio de las transacciones intersectoriales y su interdependencia dentro de las actividades productivas de una economía.
En resumen, estos índices reflejan y amplían la visión del sistema
Insumo-Producto y sus características estructurales, partiendo de la
generación y distribución de los bienes y servicios en economías regionales o nacionales; ya que informan sobre las relaciones directas e
indirectas entre las ramas de actividad o industrias y la influencia que
ejerce sobre estos los impactos de demanda final, perfilando los sectores claves en el funcionamiento del entramado económico.
II.3.2 La Matriz Insumo-Producto del Caribe colombiano
En esta sección, se hace mención al desarrollo de la Matriz InsumoProducto del Caribe colombiano, en la cual se proporciona un análisis
de los tres multiplicadores principales (producción, ingreso y empleo);
de igual manera, se destaca la posibilidad de hacer extensiones de los
Modelos Insumo-Producto de un país hacia economías regionales, incorporando el escenario del largo plazo a través de proyecciones y
pronósticos.
De allí pues, que Bonet (2000) hace referencia a los ejercicios realizados en Colombia empleando la metodología insumo producto, cuyos
enfoques se han concentrado a nivel nacional. Entre ellos, se cuenta
con un modelo keynesiano simple desarrollado por el Departamento
Nacional de Planificación DNP, el modelo SAM (Schematic Social
Accounting Matrix) de Fedesarrollo, la matriz Insumo-Producto de las
Cuentas Nacionales del DANE y la matriz de contabilidad social 1996
para Colombia del CEGA”. Por otra parte el documento presentado,
muestra el Modelo Insumo-Producto de la región Caribe colombiana,
en la cual, realiza una revisión de los elementos básicos de la metodología Insumo-Producto, características generales del modelo regional
y también se analizan los multiplicadores de producción, empleo e
ingreso regional que estima el sistema.
56
Uno de los supuestos básicos del modelo Insumo-Producto es “que el
consumo que haga una industria i del bien j dependerá exclusivamente
de la producción de la industria i”. De esta manera, se establecen coeficientes técnicos entre las industrias que señalan la participación del
consumo del bien j en la industria i sobre el total de la producción de i;
además esos coeficientes son fijos, lo que implica que hay rendimientos constantes a escala y se ignoran las economías de escala en la
producción (Bonet, 2000: p.7).
La función de producción en que se basa el MIP es similar a la aproximación microeconómica neoclásica general, en donde la producción
de una industria es función de los insumos consumidos de las diferentes industrias, de los factores de producción y de los insumos importados. Una de las primeras aproximaciones al análisis Insumo-Producto
a partir del pronóstico de demanda final de un determinado bien, es
conocer cuánto deben producir los otros sectores que sirven como insumos para satisfacer esa demanda final. Otro uso mostrado por Bonet
(2000), es la participación del modelo en el análisis del empleo, en la
medida que exista un conocimiento de las necesidades de empleo de
los sectores y de los requerimientos de producción bruta, es posible
conocer la cantidad de empleo de cada sector necesario para satisfacer
la demanda final exógena. En todo caso, se podría producir una matriz
de ocupación por industria donde se determine los diferentes tipos de
empleos demandados por cada industria, donde la suma de la columna
indica el total de empleo usado por el sector representado por esa columna y la suma de la fila señala la cantidad empleada de una particular categoría de empleo en todos los sectores.
De igual manera, uno de los aportes del trabajo de Bonet (2000), es
plantear la posibilidad de hacer extensiones de Modelos Insumo-Producto de un país hacia economías regionales y por otra parte la incorporación del escenario del largo plazo, a través de proyecciones y
pronósticos. En este sentido, a partir de una proyección de la demanda final de una región o un país y el empleo de la matriz inversa de
Leontief, se podría pronosticar la producción de todos los sectores
que es necesaria para satisfacer esa demanda final. La bondad de
57
este tipo de herramienta está determinada por la confiabilidad de las
proyecciones de la demanda final y la dinámica de los coeficientes
técnicos.
Por último, es importante destacar el análisis de los tres multiplicadores
principales: el primero, es el multiplicador de producción para un determinado sector, definido como el valor total de producción en todos
los sectores de la economía necesario para satisfacer un peso adicional
en la demanda final de la producción de ese sector. Existe el
multiplicador simple que mira el efecto sobre un sector en particular y
el multiplicador compuesto que resulta de la sumatoria de todos los
multiplicadores simples. El segundo, un multiplicador del ingreso, refleja el impacto de un cambio en la demanda final sobre el ingreso
recibido por los hogares. Finalmente, el multiplicador del empleo que
estima la relación entre el valor de producción de un sector y en el
empleo necesario en ese sector.
II.3.3 Un Análisis Input-Output de la economía balear
Este trabajo busca analizar algunos aspectos de la economía de la
Comunidad Autónoma de las Islas Baleares (CAIB), empleando la
correspondiente tabla de Insumo-Producto del año 1997 (TIOIB-97),
elaborada por la Conselleria d’Economia i Hisenda14. Por otro lado,
este es un trabajo hace énfasis en la aplicación de algunas herramientas del análisis Input-Output a la TIOIB-97 para caracterizar las
interdependencias sectoriales de la economía balear, valorar el impacto
de variaciones en la demanda turística sobre la producción y estimar el
efecto de variaciones en los salarios y en los precios de las importaciones del resto de España en la evolución de los precios locales.
14
Las tablas fueron elaboradas por un equipo de profesores del Departamento de Economía
y Empresa de la Universidad de las Illes Balears dirigido por Eugeni Aguiló e integrado
por Natividad Juaneda, Margalida Payeras, Francisco Sastre, Antoni Sastre y Elisabeth
Valle.
58
Polo y Valle (2002, p. 234) exponen que una tabla Input-Output proporciona información detallada sobre las actividades productivas realizadas dentro de un territorio económico, tanto desde el punto de vista
de la oferta como desde el punto de vista de la demanda o destino final
de la producción.
Esto ejerce significación para cualquier trabajo sobre Insumo-Producto, debido a que se muestra como deben estar estructuradas las matrices de los flujos intrasectoriales e intersectoriales. En el caso de la
TIOIB-97, la economía está desagregada en 54 ramas15, los flujos intermedios y finales aparecen desglosados por su origen en tres valores
correspondientes a producción, importaciones del resto de España (RE)
e importaciones del resto de países (RP). El valor añadido se desagrega
en los conceptos habituales de Remuneración de asalariados, Impuestos ligados a la producción, Subvenciones de explotación y un residuo
o Excedente bruto de explotación. En adición a los recursos locales
disponibles, la demanda de cada rama se satisface con las importaciones del resto de España y del resto de países. En la sección segunda se
describe las características de la TIOIB-97 y se destacan algunos rasgos sobresalientes de la economía balear empleando la información de
la tabla.
El análisis Insumo-Producto abarca numerosas aplicaciones, el supuesto
en el cual se basa “es que la estructura productiva de cada sector se
puede representar por una tecnología de coeficientes técnicos (fijos) y
rendimientos constantes de escala, conocida también como función de
producción Leontief” (Polo y Valle, 2002: p. 395). Los autores coinciden en que esta hipótesis y la noción de que los productores minimizan
el costo de producción, permite especificar los coeficientes fijos de
cada sector utilizando la información sobre flujos entre ramas y pagos
15
En realidad hay 55 ramas contando la rama ficticia correspondiente a la producción imputada
de servicios bancarios.
59
a los factores primarios que proporciona una tabla Input-Output. Por
otro lado, los coeficientes técnicos estimados pueden emplearse para
analizar las interdependencias sectoriales, estimar el efecto de variaciones en el vector de demandas netas de bienes y servicios sobre los
niveles de producción sectorial y calcular el impacto de alteraciones
en los precios de los factores o los precios de las importaciones sobre
los precios de los bienes y servicios producidos.
En resumen, Polo y Valle (2002; p. 414) mencionan que la TIOIB-97
proporciona información cuantitativa valiosa sobre la estructura de la
economía balear desagregada en las diferentes ramas características
de esta economía y una mirada a la tabla revela inmediatamente el
papel que desempeña la notable dependencia de las actividades productoras de servicios turísticos con el resto de la economía. Por otro
lado, también destaca el elevado peso de los sectores productores de
servicios y, dentro de ellos, los sectores turísticos especializados en
satisfacer la demanda de los consumidores no residentes. Como se ha
visto al analizar las interdependencias sectoriales, se trata de sectores
con una baja capacidad impulsora y estratégica. Esta circunstancia,
unida a la pequeña dimensión de la economía balear y su carácter insular, explican el escaso desarrollo alcanzado por los sectores industriales y su fuerte dependencia de las importaciones intermedias. Observado todo ello, parece inevitable concluir que para mantener una senda de bienestar creciente es absolutamente vital mantener o incluso
mejorar los atractivos turísticos de las islas.
II.4. Bases para otros estudios
El Modelo Insumo-Producto permite crear bases para otros análisis e
investigaciones, a pesar de sus restricciones, considerando principalmente lo vinculado con la evaluación de las redes sociales, construcción
de modelos de equilibrio general computable, elaboración de matrices
de contabilidad social, elaboración de modelos dinámicos de InsumoProducto, estudios econométricos, y por otro lado, análisis y construcción de multiplicadores multisectoriales; todo esto con la finalidad de
disponer de un conocimiento integrado sobre la importancia de contar
60
con las matrices Insumo-Producto para la evaluación de las características estructurales y de las relaciones intersectoriales de una economía.
II.4.1 Análisis Estructural a partir de la Teoría de las Redes Sociales
Tomando en consideración los trabajos de García y Ramos* (2002) y
**(2003), se observa la importancia de la aplicación de los Modelos
Insumo-Producto (MIP) en los estudios de las redes sociales, para interpretar los movimientos y características estructurales de una economía,
esta herramienta sirve de orientación para el desarrollo de proceso de
circulación e influencia económica dentro de la estructura considerada.
En la cual hace, una notable simplificación del esquema de relaciones
intersectoriales, ventajas que apenas han sido aprovechadas.
García y Ramos (2003, p. 3), basa su trabajo en el de Morillas (1983),
que analiza las relaciones intersectoriales a partir de la teoría de grafos,
como el antecedente de la aplicación de la disciplina de las redes sociales y en donde se coincide que uno de los aspectos fundamentales e
importantes que posibilita el conocimiento con profundidad de una
economía es la realización de un análisis de su estructura productiva.
Dicho análisis supone una importante ayuda no sólo en la toma de
decisiones de política económica, sino también constituye un requisito
indispensable y previo a las tareas de predicción necesarias en un contexto empresarial.
Por otro lado, es bueno mencionar que “las relaciones entre las redes y
cadenas apoyan la configuración de la política sectorial en los territorios económicos, de acuerdo con las nuevas perspectivas de la división
internacional de la producción y del trabajo” (Cardona, 2001: p. 261).
En este sentido, todo está basado en un concepto de red social que
“consiste en un conjunto de actores entre los que se establece una
serie de vínculos. Pueden estar constituidas por un número más o menos amplio de actores y una o más clases de relaciones entre pares de
elementos” (García y Ramos, 2003: p. 3).
61
II.4.2 Construcción de Modelos de Equilibrio General Computable
El análisis del comportamiento de los precios es esencial para observar el mecanismo de vaciado del mercado, que hacen que la oferta y
demanda se equilibren. En atención a lo planteado, Boyd e Ibarrarán
(1996) y Chiappori, Ekeland, Kübler y Polemarchakis (2002) mencionan que el objetivo de construir un modelo de equilibrio general computable es poder cuantificar el efecto de distintas políticas sobre el
crecimiento16 de los distintos sectores, sobre el consumo, los precios y
el nivel de bienestar agregado. Estos modelos de equilibrio general
presentan una versión simplificada de los sectores relevantes de la economía y las interrelaciones entre los mismos (Busetto, 2001). Además,
al introducirse una política en un sector, su efecto genera cambios en
todos los demás sectores, en el mercado de factores de producción y
en los mercados de bienes y servicios. “El impacto de cada política se
puede rastrear de un sector a otro hasta que la economía vuelve a estar
en equilibrio”, (Boyd e Ibarrarán, 1996: p. 14).
Por otro lado, Quan Kiu (2001, p. 148) refleja otro aporte de la matriz
de Insumo-Producto relacionado con el análisis de los “cocoes”, proceso que sintetiza el uso de los coeficientes de correlación en evaluación de proyectos de inversión, considerando que apenas comienzan a
implementarse las nuevas formas de utilidad de los datos de la matriz
en el ámbito microeconómico; y bajo este mismo razonamiento se puede
aplicar el cálculo para las compras intermedias, la inversión, el consumo, las exportaciones, el consumo de capital fijo, etc. Visto desde esta
perspectiva, Shoven y Whalley (1992) mencionan que el modelo InputOutput, pese a sus limitaciones, es un modelo de equilibrio general y
un ingrediente básico de los modelos de equilibrio general aplicado,
desarrollados a partir de los años 70. En este sentido, Villar (1999, p.
220) hace una caracterización de estas economías tipo Leontief, elaborando un modelo sencillo de equilibrio general, con grandes ventajas, tanto conceptuales como operativas y en particular “garantiza la
16
Véase: Takahashi (2003), Optimal balanced growth in a general multi-sector endogenous
growth model with constant returns.
62
existencia de un único vector de precios de equilibrio17 que depende
exclusivamente de la tecnología”, sin establecer supuestos sobre los
consumidores.
Los Modelos de Equilibrio General (MEG) conforman la estructura
básica, para entender los modelos multisectoriales de crecimiento
(MSG) (Jensen y Larsen, 2004), permiten ampliar los estudios de las
Matrices de Contabilidad Social (Lofgren, Lee y Robinson; 2002); y
de igual manera, se pueden estimar a partir de los MGE los niveles de
producto potencial que satisfacen los excesos de la demanda en la
economía y observar los impactos que tienen sobre el intercambio, de
choques en los niveles de precio de las exportaciones o cambios en el
gasto gubernamental (Leong, 2002).
En este mismo orden de ideas, los MEG permiten investigar cuáles
son los impactos de choques externos sobre los diferentes sectores
económicos, por ejemplo, variaciones de precios, efectos de los impuestos18, cambios en los patrones de demanda y decisiones de producción (Johnson e Islam; 2003) y (Lavoie, Mérette1 y Souissi; 2001);
también incorpora análisis de impactos de los mecanismos de estabilización macroeconómica (Clemente, Faris y Puente, 2002), en aquellas
áreas donde la variable política económica19 ejerce mayor influencia
(Hedi , Decreux, Guérin y Jean; 2002) y donde las economías de transición son más vulnerables (Zalai, 1998).
17
Véase: Brainard y Scarf (2000), How to compute equilibrium prices in 1891 y Berliant y
Dakhlia (1997). Sensitivity analysis for applied general equilibrium models in the presence
of multiple equilibrium.
18
Véase: Cardenete y Sancho (*) (2002), An applied general equilibrium model to assess the
impact of national tax changes on a regional economy.
19
Véase: Allen, R (1997), Multi-sector simulation model of soviet economics development.
63
II.4.3 Construcción de Matrices de Contabilidad Social (MCS, SAM)
Las MCS son otras representaciones del SCN en las cuales las Matrices Insumo-Producto sirven de apoyo, debido a que se incorpora los
análisis de los aspectos distributivos de la economía y además es la
base de datos para los modelos multisectoriales (de multiplicadores o de
equilibrio general). Por lo tanto, FMI, OCDE, Naciones Unidas (1993)
y Naciones Unidas (2000), conciben a las Matrices de Contabilidad
Social como herramientas muy útiles para observar la estructura económica de una entidad determinada independientemente del tamaño que
sea, y por otro lado es una fotografía que representa contablemente los
flujos de un sistema económico en un período determinado.
Las Naciones Unidas (2000) muestran la MCS como una extensión de
los MIP de Leontief y además de presentar la estructura de la producción, distribución del ingreso y la demanda, agrega información
detallada acerca de los diferente grupos sociales que ella contiene,
particularmente los hogares y su fuerza de trabajo, por ello es que la
MCS es una integración y ampliación de todo el Sistema de Cuentas
Nacionales (SCN). En este sentido, FMI, OCDE, Naciones Unidas
(1993; párrafo 19.5) destaca que “una MCS no es una alternativa al
SCN. Una MCS es el SCN, expresado en términos matriciales e incorporando cualquier grado de detalle que tenga un interés especial”; por
otro lado, en el (párrafo 20.4) se define la MCS, como:
La presentación de las cuentas del SCN mediante una matriz que establece las relaciones entre un cuadro de oferta y
utilización y las cuentas de los sectores institucionales. En
muchos casos se han aplicado MCS al análisis de las
interrelaciones entre los aspectos estructurales de una economía y a la distribución del ingreso y el gasto entre grupos
de hogares. Evidentemente, las MCS están estrechamente
relacionadas con las cuentas nacionales, con lo cual su típico
enfoque con respecto al papel de las personas en la economía puede reflejarse mediante, entre otras cosas, en aperturas
adicionales del sector de los hogares y una representación
64
desagregada de los mercados de trabajo (es decir, mediante
la distinción de varias categorías de personas ocupadas). Por
otra parte, las MCS normalmente contienen un cuadro de
oferta y utilización o un cuadro Insumo-Producto algo menos detallado.
De esta manera, el ampliar un cuadro de oferta y utilización o un cuadro de Insumo-Producto para presentar todo el flujo circular del ingreso a nivel mesoeconómico, se capta un aspecto esencial de la Matriz
de Contabilidad Social (MCS). Por ello, Kehoe (1996) ilustra el uso
de MCS en aplicaciones de calibración de los Modelos de Equilibrio
General, en la cual esta calibración puede hacerse por estimación estadística de los parámetros.
La Matriz de Contabilidad Social puede ser mostrada para un sector,
ejemplo de ello, es la aplicación que hace la Secretaría de Agricultura,
Ganadería, Pesca y Alimentos de Argentina (2002), a partir de la construcción de la MCS para el sector agroalimentario; constituyendo un
adelanto de la futura y definitiva MCS; la misma contará con una mayor apertura, enfocándose particularmente en el sector agroalimentario.
Esta herramienta tiene una gran utilidad tanto a nivel académico y en
la realización de políticas, como de interés para el empresariado argentino que trabaja en el sector agroalimentario.
Finalmente, Cardenete y Sancho (**) (2004; p.5) señalan que las Matrices de Contabilidad Social “...permiten incorporar todas las transacciones económicas y, de forma más concreta, muestra las interrelaciones
mutuas entre la estructura de producción, la distribución del ingreso y
los patrones de consumo”. Por lo tanto, facilita expandir analíticamente la información de las tablas Insumo-Producto y permite ahondar,
gracias al cierre del flujo circular de la renta, en las propiedades subyacentes en el engranaje de interrelaciones entre los tres grandes bloques de una economía (producción, demanda final y rentas).
65
II.4.4 Construcción de Modelos Dinámicos de Insumo-Producto
La construcción de modelos dinámicos de Insumo-Producto, buscan
incorporar consideraciones adicionales no tomados en cuenta por los
modelos estáticos y en la cual se llegaba a un nivel de equilibrio en el
producto de todas las industrias, en este sentido, Chiang (1987),
Takayama (1994) y Hammond (1995), coinciden que en los modelos
estáticos las incógnitas (nivel de producción necesario para satisfacer
la demanda final), se resolvían con un sistema de ecuaciones lineales
simultáneas; ahora bien, cuando se introduce al modelo ciertas consideraciones económicas adicionales, el sistema Input-Output puede tomar un carácter dinámico, y por consiguiente, el sistema se resuelve
usando ecuaciones en diferencias o diferenciales a partir de aspectos
como desfases temporales y mecanismos de ajuste.
Bajo el enfoque dinámico de Insumo-Producto Kurz y Salvadori (1998)
establecen, que sus análisis se derivan tomando en consideración las
tasas de cambio en el tiempo de las relaciones de interdependencia
intersectorial, por lo tanto, hay que enfocarse sobre las relaciones de
los stocks de instrumentos durables de producción y el flujo de insumos y productos. En realidad, muchos autores conciben al modelo de
Leontief como un modelo dinámico de crecimiento20 endógeno y de
igual manera Okuyama, Sonis y Hewings (2002) asocian el estudio
temporal de la inversa de Leontief como una formulación dinámica,
que tiene la habilidad para implementar e investigar el rol de los cambios estructurales a partir de series temporales de tablas Input-Output.
Dentro del espacio analizado del Modelo Dinámico de Insumo-Producto, Guzmán (1999), analiza un sistema dinámico de tiempo discreto que modeló una economía sectorial de Insumo-Producto no lineal
precios y cantidades, para observar comportamientos complejos caracterizados por la llamada sensibilidad de las condiciones iniciales,
por lo tanto, para algunos valores de los parámetros el modelo es
predictible y para otros el modelo es caótico. En cambio, Liew (2001),
20
Véase: Farmer y Wendner (2001), Dynamic multi-sector CGE modeling and the specification
of capital.
66
analiza y estudia este modelo dinámico incorporando dimensiones temporales, en la cual, el gasto de inversión está altamente vinculado con
la conducta maximizadora de las firmas y los coeficientes tecnológicos y el stock de capital requerido incluye los precios variables que en
el modelo estático se consideraban fijos.
II.4.5 Estudios econométricos
Los modelos intersectoriales como el Insumo-Producto, buscan de
desarrollar estudios cuantitativos adicionales a partir de la confiabilidad
de los datos recopilados, para generar un análisis estadístico-económico mayor al que se obtiene en los modelos multisectoriales.
En las últimas décadas, han surgido trabajos empíricos relacionados
con los cambios estructurales que acompañan al crecimiento de los
países, además, se intentó describir uniformidades en el comportamiento
económico por medio de comparaciones de las economías a distintos
niveles de ingreso; ejemplo de ello es Elías y Fernández (2000) que
hacen un análisis empírico para América Latina sobre la composición
sectorial de la producción, cuyo objeto es realizar un análisis
exploratorio del grado de variación de la estructura de la producción
dentro del proceso de asignación de recursos a medida que cambia el
nivel de ingreso en una versión simplificada del modelo planteado por
Chenery (1979).
Es así como, Bonet (2000, p. 3) explica los fundamentos básicos del
análisis Insumo-Producto y sus principales características dentro de
un modelo econométrico regional, con estimaciones de los
multiplicadores parciales y totales de producción, empleo e ingreso;
éstos le permitieron concluir “que los mayores efectos de
multiplicadores en producción se encuentran en el sector agropecuario, que los más importantes efectos multiplicadores de empleo se generan en la industria manufacturera y que los efectos multiplicadores
de ingresos mayores se dan en los sectores de servicios”.
67
También es importante mencionar, que Word y O’Neill (2001) consideran importante el análisis econométrico para observar los efectos
finales de una perturbación sobre los coeficientes técnicos de la matriz
Insumo-Producto, partiendo del análisis estático de Leontief y determinando cuanto puede producir una industria de un producto para la
demanda final de ese producto. En este sentido, Guo y Planning (2000),
usan el análisis Insumo-Producto para observar cambios estructurales
de la economía de los Estados Unidos desde 1972 a 1996, proporcionando herramientas necesarias para evaluar industrias, su relación con
el resto de la economía y los efectos del intercambio internacional de
esas interrelaciones.
Finalmente, Martínez, Morales y Valdez (2001), hacen un análisis
empírico sobre los cambios estructurales en la demanda por trabajo en
Chile, a partir de los análisis de elasticidad empleo-producto, en cambio, West y Brown (2003) analizan los cambios estructurales en la
economía taiwanense para el período 1976-1994, usando series de tablas Input-Output21. En consonancia con la anterior, es evidente que
resulta importante contar con un mantenimiento continuo del Modelo
Insumo-Producto para contrastar las características estructurales de
una economía con la ayuda de los modelos econométricos.
II.4.6 Análisis y construcción de multiplicadores multisectoriales
Los modelos intersectoriales como el Modelo Insumo-Producto, permiten calcular y analizar las estructuras productivas específicas de un
país, en atención a lo planteado, el objetivo central del Instituto Nacional de Estadística e Informática de Perú (2001), consistió en elaborar
un conjunto de multiplicadores de la economía peruana, para analizar
y evaluar la importancia relativa de los sectores económicos. La metodología y resultados que se presentan en este documento están referidos
a los multiplicadores del PIB, empleo y divisas. De igual manera, el
derivar este conjunto de multiplicadores permiten un mejor conoci21
Véase también: Zakarias, Fritz, Pointner y Steiner (2001). An Input-Output analysis of
regional clusters.
68
miento de la importancia relativa de los sectores económicos considerados en la matriz Insumo-Producto, aunado a que se sintetizan las
características de la estructura productiva del país que son difíciles de
visualizar en forma agregada.
Por otro lado, Ball y De Sastre (2002), destacan la importancia de
construir y analizar los multiplicadores keynesianos aplicados al gasto
turístico en países o regiones, es decir, el multiplicador turístico, con la
finalidad de que logren contener el conjunto de impactos que producen
en la economía los diferentes cambios originado por el flujo de visitantes extranjeros a cada país; ya sea en forma directa, indirecta o inducida, en términos de creación de valor, empleos y generación de divisas.
Adicionalmente, los análisis de los multiplicadores son claves para
comprender las estructura económica de un país o de una unidad productiva (Cañada, 1997), es por ello que fue el tema central en los Cluster y encadenamientos productivos de la II región 200, en el Seminario
de la 53a Convención Anual del Instituto de Ingenieros de Minas de
Chile, en el que se concluyó que los multiplicadores sectoriales permiten medir el impacto para toda la economía y no sólo para un sector en
específico.
69
III. LA PRODUCCIÓN SECUNDARIA
Y EL MODELO INSUMO-PRODUCTO (MIP)
Este capítulo intenta mostrar un análisis extenso sobre el tratamiento
de los productos secundarios en el Modelo Insumo-Producto, ya que
lo ideal en la construcción de la matriz de Leontief es contar con aquellas actividades que producen un único bien y así conservar la homogeneidad en la función de producción (supuesto básico del modelo).
Por consiguiente, la presencia de productos secundarios es común y
normal en todas las economías, así que es necesario su estudio y evaluación, con la finalidad de obtener una función de producción de
Leontief asociada a un único producto.
El desarrollo de este capítulo, se basa en lo considerado por el Manual
sobre la compilación y el análisis de los cuadros Insumo-Producto de
las Naciones Unidas (2000), en la cual se describe cuáles son los métodos para el tratamiento de la producción secundaria, sin embargo, se
destaca que hasta la fecha no hay soluciones satisfactorias para la separación de los productos secundarios en los cuadros de Insumo-Producto, por lo tanto, las soluciones ofrecidas no llegan a ser óptimas,
pero resuelven las inconsistencias provocadas por la no homogeneidad de la función de la producción.
III.1 Visión general
Uno de los detalles fundamentales para la construcción de los cuadros
Insumo-Producto es contar con información más detallada sobre todos
los procesos de producción que intervienen en una economía. Si se
tiene información adicional sobre el producto bruto, el valor agregado
y la demanda final, es posible recrear un cuadro de flujos usando la
matriz de coeficientes técnicos de Insumo-Producto y los precios de
los productos, verificando de este modo la exactitud y la compatibilidad de la información técnica con los datos sobre el valor agregado y
la demanda final cuando se equilibra por último el cuadro. “La cons-
70
trucción de los cuadros Insumo-Producto en términos físicos no es
sencilla, porque las empresas quizás no estén dispuestas a revelar ciertos detalles técnicos de sus procesos de producción” (Naciones Unidas, 2000: párr. 4.2).
La compilación de los cuadros Insumo-Producto ha dependido principalmente de los datos proporcionados por los censos de los establecimientos y de las encuestas especiales; en este sentido, obtenerse todos
los datos técnicos por encuestas especiales, independientes de los censos, es algo que puede resultar muy costoso. Por otro lado, las Naciones Unidas (2000, párr. 4.1 y 4.2) consideran que “lo ideal para la
construcción de un cuadro simétrico de Insumo-Producto es contar
con datos que describan la estructura de insumos de cada tipo de actividad que produce un único bien o servicio en la economía”. La finalidad de conservar la homogeneidad de la función de producción, es no
permitir que exista distorsión en el análisis Insumo-Producto, sobre
todo cuando los efectos totales o agregados se calculan usando la inversa de Leontief; y por consiguiente, cada industria de un cuadro de
Insumo-Producto debe ser lo más homogénea posible cuando se lo usa
como instrumento para el análisis.
A diferencia de esta situación ideal, los Cuadros de Oferta y Utilización (COU) del SCN son marco integrado para las estadísticas de producción, diseñados para que sirvan como la mejor herramienta
estadística para la compilación de los agregados de las cuentas nacionales y para que proporcionen información necesaria para la compilación del cuadro simétrico de Insumo-Producto. Por consiguiente, para
no tener que utilizar encuestas complementarias o vivir con los problemas
de los productos secundarios y resolverlos con métodos mecánicos,
los estadísticos que se dedican al Insumo-Producto deberían planificar
los datos que tratarán de reunir los censos. La estrategia es, en lo posible, definir en forma operativa un establecimiento, si se hace esto, se
eliminará de los COU la mayoría de los productos secundarios y como
último recurso se usarán los métodos matemáticos que son básicamente mecánicos (Naciones Unidas, 2000).
71
Si se observa la matriz cuadrada de oferta del COU, es una matriz que
en su diagonal principal encontramos aquellos productos que son principales en la actividad que los genera y los elementos no diagonales
son sus producciones secundarias, por lo tanto, en orden de trabajar
con una función de producción homogénea es necesario concentrarse
en usar métodos estadísticos o matemáticos dependiendo del tipo de
producción secundaria generada. En esta perspectiva, Cañada (1997,
p. 35) menciona, que para analizar de forma más detallada el proceso
de producción es necesario definir un tipo de unidad analítica que por
lo general no es observable directamente en el mundo real: “la unidad
de producción homogénea”, ésta se caracteriza por desarrollar una sola
actividad, sin la existencia de actividades secundarias (aunque obviamente sí podemos encontrar actividades auxiliares).
III.2 Clases de productos secundarios
1. Productos secundarios originados en prácticas estadísticas
Los productos secundarios pueden ser el resultado de prácticas estadísticas menos refinadas que no siguen la definición de establecimiento que se hace en el (FMI, OCDE, Naciones Unidas, 1993: párrafo
2.55), estas prácticas pueden tener su origen en la forma de representar los datos de la producción de la forma más realista posible y adopta
a la empresa como una unidad estadística.
Cabe considerar, que si se usa a la empresa como unidad estadística y
se encuentra un establecimiento múltiple que produce más de un producto, surge el problema de productos secundarios, es decir, en el cuadro de oferta se registrará más de un producto para la misma industria.
También ocurrirá presencia de productos secundarios, en el caso de
empresas o establecimientos integrados verticalmente que no se separaran en establecimientos como lo recomienda el SCN y en el caso de
una empresa integrada horizontalmente que opera en un emplazamiento produciendo distintos productos para su venta en el mercado. Pero
aunque sea evidente, que cada producto se produce por medio de una
tecnología distinta, los datos sobre la producción se reúnen en forma
agregada y se trata a la empresa como si fuera un único establecimiento.
72
Es por ello, que el Instituto Nacional de Estadísticas (INE) (1995,
p. 1) de España en la nota metodológica sobre la tabla simétrica de
Input-Output de la Economía Española establece en concreto, que debe
acercarse la construcción de los Modelos de Insumo-Producto a los
principios de Leontief, es decir, que las tablas matriciales deben responder a un esquema de “Producción simple”: es decir, que las columnas
de las matrices de consumos intermedios e insumos primarios reflejen
las funciones de “producción” de un tipo de producto concreto. Para
ello se definen unas ramas de actividad que son “conceptuales” en el
sentido de que son creadas por los contables nacionales y que se denominan “ramas de actividad homogénea”. Cada rama de actividad homogénea representa las estructuras de producción (costos) de un
tipo exclusivo de producto en el sistema económico (de acuerdo obviamente con el nivel de desagregación elegido).
Por otro lado, las Naciones Unidas (2000, párr. 4.10), manifiesta que
aunque se adopten completamente las recomendaciones del SCN, “seguirán apareciendo productos secundarios en tanto las actividades que
los producen no se identifiquen como establecimientos separados, pero
en este caso habrá menos productos secundarios y por lo general el
problema se resolverá después mecánicamente”.
2. Productos secundarios atribuibles a la tecnología
de producción
En el caso de tecnologías que producen más de un producto simultáneamente y también pueden producirse productos similares en otros
lugares mediante otras técnicas muy distintas de producción, las Naciones Unidas (2000, párr. 4.11), distingue tres clases:
a)
Los subproductos exclusivos son aquellos que no se producen
por separado en ningún otro lugar (melaza vinculara a la producción de azúcar, chatarras en las industrias metalúrgicas).
b)
Los productos ordinarios son aquellos vinculados tecnológicamente a la producción de otros productos, pero, que se producen
73
como productos principales (hidrógeno subproducto de las refinerías de petróleo que también es producido por separado por
otros establecimientos de la industria química).
c)
Los productos conexos son aquellos que tiene vinculación tecnológica menos estrecha que los subproductos ordinarios; los
costos que comparten estos subproductos tiene un valor más significativo que los subproductos ordinarios, (ejemplo: la leche y
carne en la industria ganadera) que pueden producirse en una escala que depende de la demanda de cada producto y la relación
entre ambos puede variar frente a la modificación de la demanda.
Uno de los productos conexos puede ser producido por separado
en otro lado. No es fácil distinguir entre productos conexos y
subproductos.
III.3 Separación de las empresas en unidades homogéneas
Desde el levantamiento de la información de la unidad empresa puede
proporcionar estadísticas sobre las actividades productivas, sobre el
estado de ganancias y pérdidas (ingresos y gastos), y balance general
(los activos, pasivos y patrimonio). Esta empresa puede llevar a cabo
más de una actividad, al manifestarse esto, no debe ser utilizada como
unidad estadística para las cuentas de producción de las cuales se parte
para los cuadros Insumo-Producto, porque la tecnología de producción de la empresa no es homogénea, es decir, a cada actividad económica tiene que tener asociada una tecnología de producción. En este
caso, Naciones Unidas (2000, párr. 4.12), recomienda que la empresa
se divida en establecimientos separados, cada uno de los cuales realiza sólo una actividad productiva, y en este sentido en el cuadro de
Insumo-Producto, una industria se definirá como un grupo de establecimientos que se dedica al mismo tipo de actividad productiva”.
Cortés y Pinzón (2001, p. 173), coinciden que la unidad de producción
homogénea se utiliza para la elaboración de las matrices de InsumoProducto y para este análisis se requieren unidades que se dediquen
74
únicamente a una actividad productiva. Por otro lado manifiesta, que
si un establecimiento tiene una producción principal y una o varias
secundarias, de dividirse en el mismo número de unidades de producción homogéneas. Esto en la práctica no siempre es posible y para
llegar a un acercamiento significativo debe usar supuestos e hipótesis
de trabajo.
La mejor forma de obtener las aperturas de insumos y productos como
unidades de producción homogénea de una empresa, es que los encargados de reunir los datos pidan que se los hagan y den instrucciones
precisas, para que no se tenga que recurrir a métodos mecánicos para
separarlos en una etapa posterior. Para ello, a continuación se enuncian algunas normas que recomienda el SCN para dividir las empresas
en unidades de producción homogénea.
III.3.2 Normas generales del SCN para crear un establecimiento separado
Un establecimiento, según el FMI, OCDE, Naciones Unidas (1993:
párrafo 5.21), es “una empresa o parte de una empresa situada en un
único emplazamiento y en el que sólo se realiza una actividad productiva (no auxiliar) o en el que la actividad productiva principal representa la mayor parte del valor agregado”. Para ser un establecimiento,
la unidad debe tener la capacidad de proporcionar los productos que
produce y los insumos que utiliza, la cantidad de personas que emplea,
los activos fijos y las variaciones de existencias usadas, consumidas y
colocadas durante el período contable.
Según las Naciones Unidas (2000, párr. 4.15), la definición del SCN
(1993) de establecimiento, permite que haya actividades secundarias
que dan por resultado productos secundarios. Por consiguiente, la definición operativa es inexacta y en consecuencia los compiladores del
cuadro simétrico de Insumo-Producto, deben separar de alguna forma
los productos secundarios y los insumos asociados.
75
El cuadro de Insumo-Producto sería más confiable si la separación la
hicieran los contadores de la empresa en la fuente original de los datos,
siempre que sea posible, asignar costos a cada producto que produce
el establecimiento, cosa que hacen comúnmente para determinar los
precios de los productos.
La mayoría de los insumos que utiliza cada establecimiento y los productos que producen pueden ser presentados en detalle por los contadores. Pero hay otros costos que comparten todos los establecimientos
dentro de la empresa, costos que en general son generados por actividades auxiliares, como el procesamiento y la comunicación de información, el transporte, el almacenamiento, las compras, la promoción
de las ventas, el mantenimiento y la seguridad que se necesitan para
apoyar las principales actividades productivas de la empresa. Estas
actividades no pueden tomarse por separado; lo que deberían es integrarse con las actividades principales y asignar sus costos a cada actividad principal. No deben separarse como si fueran establecimientos
sino que los insumos que utilizan deben asignarse a los establecimientos a los que prestan servicios.
No obstante, existen especificaciones y caso particulares, para algunas actividades que no deben tratarse como auxiliares sino como actividades productivas y separarse como un establecimiento. Entre ellas,
cabe mencionar: la producción de bienes para su ulterior procesamiento en la misma empresa integrada verticalmente, por ejemplo, la extracción de petróleo crudo para luego obtener productos refinados, la
construcción por cuenta propia de parte de los hogares, el gobierno o
las empresas y la exploración minera para descubrir nuevos depósitos
cuando es iniciada por cuenta propia por las empresas, entre otras (Naciones Unidas, 2000: párr. 4.16 y 4.17).
76
III.3.2 Separación de la construcción por cuenta propia
y las actividades integradas verticalmente
Según las Naciones Unidas (2000, párr. 4.18), “la separación de las
actividades secundarias de las principales, por ejemplo, la separación
de la construcción por cuenta propia de otras actividades o de las que
se integran verticalmente, como ocurre en una industria petrolera integrada que combina la extracción de crudo y la refinación, normalmente se hace valorando los productos al costo”. Para ponerlo en práctica
esta separación en un cuadro de Insumo-Producto, hay que separar
todos los costos correspondientes a la actividad, el excedente de explotación de la empresa en un conjunto tiene que distribuirse proporcionalmente a cada actividad sobre la base del valor agregado menos
el excedente de explotación y distinguirse al menos un establecimiento
en cada actividad.
III.3.3 Distribución de los costos de actividades auxiliares
a los establecimientos
Para distribuir los costos de actividades auxiliares a los establecimientos, el SCN (1993), recomienda que el costo de estas actividades se
distribuya en todos los establecimientos a los que presta servicios, en
cambio las Naciones Unidas (2000, párr. 4.19), establece que cuando
el establecimiento se usa como una unidad estadística para las cuentas
de producción, hay que abordar el problema de la distribución de los
costos de las actividades auxiliares en empresas con múltiples establecimientos. En este caso, si hay registros contables que revelan cuánto
es el costo central atribuible a cada uno de los establecimientos separados, se los debe distribuir sobre esta base. Si no se dispone de la
información necesaria, el costo de cada insumo consumido por la unidad central debería distribuirse entre los establecimientos a los que
sirve, en proporción al valor de la producción de cada establecimiento
menos el valor de los costos intermedios, excluidos los costos de las
actividades auxiliares mismas. Si también este método resulta demasiado difícil de aplicar, el costo de cada insumo central puede distribuirse
77
simplemente en proporción al valor de los productos de los establecimientos a los que sirve.
III.3.4 Actividades auxiliares con ventas
Cuando hay empresas que venden parte de los servicios auxiliares a
otras empresas, por ejemplo, una base de datos en una computadora,
un sistema contable o un depósito para almacenamiento pueden desarrollarse primero para usos internos, para atraer a otros clientes más
adelante; las Naciones Unidas (2000, párr. 4.20), menciona que el SCN
1993 recomienda que en estas unidades auxiliares, con ventas de la
mitad o más de su producción se les deben tratar como establecimientos separados. La producción utilizada internamente se tratará como
servicios consumidos con valores imputados al establecimiento de reciente creación. Cuando una unidad auxiliar no se clasifica como un
establecimiento separado, aunque parte de su producción se venda en
el mercado, además de la producción de la actividad principal, la producción secundaria aparecerá en el cuadro de oferta. Esta producción
secundaria denota la producción de la unidad auxiliar que se vende.
Por supuesto, si las empresas se usan como unidades estadísticas para
las cuentas de producción, aparecerán más productos secundarios en
el cuadro de oferta del marco Insumo-Producto.
Al recomendar el establecimiento como unidad estadística, el SCN
trata de reducir el problema del producto secundario en el momento
que se quiera obtener cuadros simétricos de Insumo-Producto; la práctica común es ocultarlos mediante la agregación o recurrir a los métodos
matemáticos sobre algunos supuestos para reclasificar a los productos
secundarios y los insumos relacionados. Pero lo único que hace esta
reclasificación es crear un establecimiento separado de la producción
de mercado de las unidades auxiliares.
Aunque el SCN no recomienda esto, es mejor eliminar los productos
secundarios por métodos estadísticos que usando los matemáticos cuando se trata de obtener el cuadro simétrico de Insumo-Producto. La
78
asignación de los costos se hace en forma similar al procedimiento
descrito. En este caso, la producción de la misma unidad auxiliar se
tratará como si fueran productos diferentes, ya que se venden a precios
distintos.
III.3.5 El método de la redefinición
Se trata de un método muy parecido al matemático, éste se basa en el
supuesto de tecnología de producto, con la excepción de que los
compiladores pueden intervenir directamente en la decisión de cuáles
son los insumos independientes que se asignarán a los productos secundarios. Como en efecto, los datos se reúnen tomando el establecimiento como base y éstos constan de productos secundarios que no
son subproductos o productos conexos resultantes del proceso de producción, sigue siendo conveniente reunir los datos de los insumos independientemente para los productos secundarios de la misma clase y
usar esta información para estimar los insumos asociados con los productos secundarios y sacarlos por transferencia. Si se hace esto, los
compiladores de Insumo-Producto tal vez puedan juzgar la calidad de
información; ésta es la esencia del método de la redefinición, aunque
requiere información adicional, (Naciones Unidas, 2000).
III.4 Tratamiento de los productos secundarios que se originan
en la tecnología de producto22
Para el tratamiento de los productos secundarios, las Naciones Unidas
(2000, párr. 4.25), recalcan que hasta la fecha no hay soluciones satisfactorias para la separación de los subproductos y productos conexos
(productos secundarios) en los cuadros de Insumo-Producto, y sólo se
ofrecen soluciones que no llegan a ser óptimas. Algunas de ellas tal
vez sean muy aceptables si los cuadros están bastante desagregados y
detallados, pero rara vez ocurre así. Por la otra parte, el problema qui22
Esto se basa en parte en “Practices in Input-Output table compilation” por Vu Luang Viet
en Regional science and urban economics, Países Bajos, Vol. 24, No. 1, 1994. Citado por
Naciones Unidas, (2000).
79
zás se haya exagerado un poco, porque los subproductos y los productos
conexos no son tan comunes en una economía y en general los valores
son bajos frente a los productos principales, por la cual quizás sean
aceptables soluciones subóptimas.
III.4.1 Métodos manuales o mecánicos
Se usan tres métodos para separar productos e insumos de subproductos
y productos conexos, conocidos como métodos manuales o mecánicos; uno de ellos es el método de transferencia negativa de desarrollo
por Richard Stone citado por Naciones Unidas (2000), en el cual sólo
se transfiere la producción; el método de transferencia positiva o agregación, en el cual la producción y los insumos de los subproductos
quedan incluidos en el producto principal de la industria en el que se
producen, y un tercer método en el que tanto la producción como los
insumos son transferidos a los subproductos y productos conexos a los
que pertenece característicamente, denominado método de transferencia de insumos y productos.
III.4.1.1 El método de la transferencia negativa
El método de transferencia negativa fue desarrollado por Stone, en
general se usa para subproductos exclusivos en el cual se transfiere
esta producción al consumo intermedio de la industria o actividad con
signo negativo. Este método tiene repercusiones para los análisis de
Insumo-Producto, como el mostrar cantidades de insumos negativos a
causa de la transferencia.
Este método se usa para los subproductos ordinarios que se producen
también en otra parte, por otro lado, deben agregarse a la columna de
insumos del subproducto de los insumos de productos idénticos que
son producidos en otra parte como principales. El método de la transferencia negativa que se aplica en este caso, dará lugar a distorsiones
en análisis posteriores, ya que pueden haber variaciones de la proporción del subproducto en el mercado, al producto idéntico al que fue
80
producido en otro lado, en los pesos relativos correspondientes a la
producción de la industria que produce el subproducto y en la producción de las industrias que usan como el subproducto como insumo
(Naciones Unidas, 2000).
En resumen, cuando se usa el método de transferencia negativa se debe
tener mucha cautela al interpretar los datos finales después de la aplicación de la inversa de Leontief. Por consiguiente, este método sólo
será viable como base para el análisis, en tanto la industria de los
subproductos no se agregue con otras industrias, ya que al identificar
los subproductos y la industria correspondiente por separado, será
posible analizar en forma más explicita las modificaciones de las participaciones en el mercado.
III.4.1.2 El método de agregación o transferencia positiva
El método de transferencia positiva lo utilizan en el caso de
subproductos exclusivos; cuando se sigue este método, los subproductos
exclusivos se tratan como si fueran productos primarios de la industria
en la que se producen, por lo tanto, es un método de agregación en la
cual la producción y los insumos de los subproductos quedan incluidos
dentro de la producción principal de la industria en el que se producen.
Si se usa este método, no será posible detectar cambios estructurales
en la utilización del subproducto como ocurría en el método de transferencia negativa, ya que el subproducto no se identifica por separado.
Este método tiene un defecto importante, que la estructura de insumos
de la industria que produce estos productos como primarios, se
distorsiona al incluir compra ficticia. En consecuencia, cuando la demanda del producto aumenta, también lo hace la producción de la industria que produce este producto como subproducto, algo que por
cierto no es verdad. Es por ello, que el método de transferencia negativa es preferible para tratar subproductos exclusivos (Naciones Unidas, 2000: párr. 4.36).
81
III.4.1.3 Transferencia de productos e insumos
Para el caso de subproductos ordinarios y productos conexos, se puede recurrir al método de la redefinición para transferir tanto productos
como insumos, si se tiene información separada sobre los insumos y
acerca de los productos similares que son producidos en otra parte.
Quizás este método sea arbitrario, puesto que el supuesto de similitud
es erróneo, pero hasta la fecha no parece haber otro método para tratar
en forma apropiada los subproductos ordinarios.
En resumidas cuentas, en este método tanto la producción como los
insumos son transferidos a los subproductos y productos conexos, a
los cuales pertenecen característicamente. En este sentido, para el caso
de los subproductos ordinarios hay una ventaja en la aplicación de este
procedimiento, sobre todo cuando el producto en cuestión se produce
principalmente por separado. El empleo de este procedimiento podría
criticarse con razón sobre la base de que no se debe separar los
subproductos del producto principal, ya que no se necesitan insumos
adicionales, como ocurría en los ejemplos presentados en los métodos
anteriores. Un ejemplo que puede observarse claramente, es el hidrógeno como un subproducto de la redefinición del petróleo, tiene como
mínimo que embotellarse antes de llegar al mercado. Cuanto más específico sean los costos que se necesitan para elaborar un subproducto,
más razonable será el argumento para asignar los costos al subproducto. Además, cuando los productores de la producción principal y del
subproducto toman decisiones acerca de la producción compararán
siempre los ingresos que devengan el subproducto de los costos correspondientes (Naciones Unidas, 2000: párr. 4.38).
III.4.2 Métodos matemáticos
Desde una perspectiva más general, es importante mencionar que
hasta la fecha no existen métodos matemáticos, que puedan derivar
satisfactoriamente el cuadro simétrico de los coeficientes de InsumoProducto, la cual, es el elemento central de la economía de Insumo-Producto, tanto desde el punto de vista conceptual como del práctico.
82
Sin embargo, estos métodos seguirán siendo necesarios como último
recurso dado que se ha utilizado cabalmente toda la información posible.
Por otro lado, se sabe que los COU no tienen que ser cuadrados, de
hecho, puede haber un número mayor de productos que de industrias
(productores) y a la inversa. En estos casos, tanto el cuadro de utilización como el de producción son rectangulares, por lo tanto, es necesario hacer un procedimiento para obtener una matriz Insumo-Producto
cuadrada o simétrica, es decir, sólo una matriz cuadrada puede invertirse
para obtener la inversa de Leontief.
Debe señalarse, que existen básicamente dos métodos de combinar
matemáticamente las matrices de producción y utilización23, para generar la matriz simétrica de Insumo-Producto tradicional; estos métodos se basan en el supuesto de la tecnología industrial o en el supuesto
de la tecnología de producción. El primero, estima que los insumos
son consumidos en las mismas proporciones por cada producto conocido de una industria dada, lo que significa que el producto principal y
los secundarios se producen todos empleando la misma tecnología, es
decir, la misma estructura de insumos; por consiguiente, este método
se le utiliza por dos razones principalmente: 1) el método siempre genera cuadros simétricos de Insumo-Producto, 2) se aplica al caso de
los cuadros rectangulares de Insumo-Producto. Pero la desventaja, es
que el método infringe la regla económica fundamental de que los productos tienen precios distintos en un momento dado, y por lo tanto,
deben reflejar costos diferentes (Naciones Unidas, 2000: párr. 4.42).
El segundo método, parte del supuesto que la estructura de insumo de
la tecnología que produce un determinado producto es la misma, independientemente del lugar donde se le produce; es más razonable desde
el punto de vista económico que el de la tecnología de la industria,
pero no se lo usa en forma generalizada, porque tiende a generar cua23
La matriz de producción se refiere a la parte del cuadro de oferta que describe la producción
interna, la matriz de utilización es la parte del cuadro de utilización que describe el consumo
intermedio.
83
dros simétricos Insumo-Producto con coeficientes técnicos negativos
y por otro lado, requiere que las matrices de producción e intermedias
de cuadros de oferta y utilización sean cuadradas, (Naciones Unidas,
2000: párr. 4.42).
Para eliminar los coeficientes negativos del segundo método que en su
mayoría son pequeños y producir cuadros simétricos positivos, las
Naciones Unidas (2000, párr. 4.44), establece que se puede: i) llevar a
cero todos los valores negativos y usar la técnica RAS para equilibrar
el cuadro y ii) optimizar, como la minimización de la varianza con
restricciones permite generar valores positivos. Sin embargo, este último también se cuestiona por otras razones, como la justificación económica de una forma específica de la función objetivo. Con una óptica
económica, el supuesto de la tecnología de producción tiene más sentido que el de la tecnología de la industria.
Para exponer los dos métodos matemáticos en las siguientes secciones, sobre la base de las siguientes notaciones y definiciones en concordancia con (Naciones Unidas, 2000: párr. 4.45).
m
n
Umxn
Bmxn
Mmxn
Dnxm
gn
qm
qˆ
Número de productos
Número de industrias
La matriz intermedia del cuadro de utilización
(producto por industria)
La matriz de coeficientes de utilización
(producto por industria)
La matriz de producción (producto por industria),
parte de la matriz de oferta que describe la
producción interna.
La matriz de participación en el mercado
(industria por producto)
El vector de producción industrial
El vector de producción de productos
La matriz diagonal del producto industrial
La matriz diagonal de producción de productos
84
Aquella matriz en el que se le observe “ˆ” es la versión diagonal del
vector que tiene la misma notación; todos los elementos fuera de la
diagonal son ceros. Por ejemplo,
⎡ g1
g = ⎢⎢ 0
⎢⎣ 0
0
g2
0⎤
0 ⎥⎥
g 3 ⎥⎦
Definiciones básicas:
B = Ug^ -1
(1)
D = M/q^ -1
(2)
III.4.2.1 Supuesto de la tecnología de la industria
Según Naciones Unidas (2000, párr. 4.48), menciona que bajo este
supuesto, un producto j puede ser producido por varias industrias k;
cada industria k necesita bik del insumo i por cada unidad de producción industrial j, donde bik con (i = 1...n) representa la tecnología industrial de la industria k, y cada industria k tiene sólo una parte del
mercado del producto j. Esta parte del mercado industrial de la industria k en la producción del producto j tiene la notación bkj. De modo
que todos los insumos i que necesitan los diferentes productores para
producir una unidad del producto j pueden escribirse en la forma
siguiente:
n
aI,ij = ∑ bik dkj
(3)
k=1
(3) muestra que el insumo i requerido para una unidad del producto j
es un promedio ponderado de las estructuras de insumos de los productores que producen el producto j y las ponderaciones son las participaciones del mercado de cada producto en la producción del producto j.
85
(3) en forma matricial, se escribe:
AI,cc = BD
(4)
AI,cc es la matriz de coeficientes de Insumo-Producto que describe los
productos que se necesitan directamente para producir otros productos, en la cual, I es igual a la tecnología de la industria y cc al orden de
la matriz
g^ A que es producto por producto. Esto se observa, que como B
es una matriz de producción producto por industria, D es industria por
producto; por lo tanto la matriz AI,cc es una matriz producto por producto.
Si se plantea la ecuación básica (5) que se derivará más adelante, se
puede usarse para mostrar y calcular distintos tipos de modelos simétricos de Insumo-Producto.
q = Bg + YC
(5)
a) Modelo Insumo-Producto, producto por producto: calcula el efecto
de una demanda final de productos en su producción.
b) Modelo Insumo-Producto, industria por industria; calcula el efecto
de una demanda final de productos industriales en la producción de las
industrias.
c) Modelo Insumo-Producto, industria por producto; calcula el efecto
de una demanda final de productos en la producción de las industrias.
Estos modelos que pueden derivarse del supuesto de la tecnología de
la industria, pero es necesario describir primero las relaciones básicas
de los cuadros de oferta y utilización a precios básicos.
La relación básica en el cuadro de utilización es
q = Bg + YC
(5)
86
YC es el vector de demanda final de productos y YI la demanda de
productos industriales.
g = Dq
(6)
YI = DYC
(7)
a) Modelo Insumo-Producto, producto por producto
Se sustituye g por la ecuación (6) en (5).
q = BDq + YC
Entonces
(I - BD)q = YC
(8)
(9)
La ecuación (9) puede usarse tanto para calcular el impacto del vector
de demanda final YC en q. Por otro lado, si se usa la matriz producto
por producto AI,cc = BD que se muestra en las ecuaciones (9) y (4), es
posible calcular el flujo de producto, impuestos y valor agregado que
se necesitan para el cuadro de Insumo-Producto (producto
por producto).
b) Modelo Insumo-Producto, industria por industria
Si se multiplica ambos miembros de la ecuación (5) por D y luego se
reemplaza DYC y Dq por las relaciones de las ecuaciones (6) y (7), se
obtiene
Dq = DBg +DYC
(10)
g = DBg +YI
(11)
(I - BD)g = YI
(12)
Este modelo se puede usar para calcular el impacto de una demanda
final de productos industriales (YI) en la producción industrial y así
reordenar el cuadro de utilización. Sin embargo, este modelo casi no
tiene interés alguno para los analistas puesto que la demanda final rara
vez está en función de la producción industrial.
87
c) Modelo Insumo-Producto, industria por producto
Sustituyendo YI por DYC en la ecuación (12) se tiene
(I - BD)g = DYC
o
g = (I - BD)-1 DYC
(13)
(14)
Este modelo puede utilizarse para calcular el impacto de una demanda
final de productos, YC, en la producción industrial. Pero no puede usarse
para ordenar el cuadro Insumo-Producto en forma significativa porque
ahora la demanda final se clasifica por productos y la producción se
clasifica por industrias (Naciones Unidas, 2000: párr. 4.62).
III.4.2.2 Supuesto de la tecnología de producción
Este supuesto se basa en la premisa básica, que la producción de un
determinado producto o mercancía, usa la misma estructura de insumos, cualquiera sea la industria en la que se lo produce (Naciones
Unidas, 2000).
Esto puede escribirse
n
uij = ∑ aik mjk
(15)
k=1
Donde uij es el insumo i requerido por la industria j, mjk es el producto
k producido por la industria j y aik es el insumo i que necesita para
producir una unida del producto k. Puesto que la industria produce
varios tipos de productos y cada uno de ellos necesita un conjunto
distinto de insumos, la cantidad de insumos que requiere la industria j
será la suma de los insumos i requeridos para cada uno de sus productos mjk, La ecuación 4.5 puede escribirse en la siguiente forma matricial:
U = AC,cc M
(16)
entonces,
UM-1 = AC,cc
(17)
88
C se refiere al supuesto de la tecnología de producción, cc al orden de
la matriz A que es producto por producto. Como U es una matriz producto por industria y M un producto por industria, entonces A debe ser
una matriz producto por producto. La ecuación de (17) implica una
fuerte restricción del supuesto de la tecnología de producción, es decir, M puede invertirse sólo si es cuadrada o la cantidad de industrias
es igual a la cantidad de productos. Esta exigencia matemática no es
realista puesto que la cantidad de industrias no necesita ser igual a la
cantidad de productos a menos que los estadísticos lo hagan mediante
la agregación.
Para probar que AC,cc es lo mismo que BC-1
C = Mg^ -1
(18)
^ -1 ^g) que es una matriz de
La prueba es la siguiente: si se inserta (g
identidad, en el medio del miembro derecho de la ecuación (17), entonces:
^ M-1 = (Ug^-1 )( g
^ M-1)= BC-1
AC,cc = U(g^-1 g)
(19)
donde C-1=( g^ M-1)
La ecuación (17) puede usarse para vincular directamente producciones de productos para una demanda final de productos; y para relacionar producciones industriales con una demanda final de productos, es
necesario reemplazar q en la ecuación (5) por Cg (esta relación se basa
en el supuesto de la tecnología de producción)24.
g = C-1 Bg + C-1 YC
ó
g = (I-C-1 B)-1C-1 YC
(20)
(21)
La ecuación (21) es una alternativa para la ecuación (14).
24
q = Cg puede obtenerse de la forma siguiente g = gi^ = (C-1 M)i = C-1 (Mi) = C-1 q.
89
Si se observa la ecuación (17), la inversión de la matriz M requiere que
la cantidad de productos sea igual a la cantidad de industrias. Por lo
tanto, una matriz rectangular no resulta aplicable cuando se usa el
supuesto de tecnología de producción. Este requisito, que no es tan
restrictivo como parece, significa meramente que para sacar por transferencia cualquier producto secundario, debe haber un productor que
lo produce en otra parte, de modo que sus insumos pueden usarse para
eliminar los insumos del producto secundario. Otros productos que se
obtienen sólo como subproductos tienen que tratarse por agregación
como si fueran parte de los productos primarios (Naciones Unidas,
2000: párr. 4.67).
Si observamos los resultados de la ecuación (17) en el caso de una
economía de dos industrias, donde la primera de ellas produce un producto secundario:
Donde U =
AC,cc
⎡u
11
⎣ u 21
u12 ⎤
⎡ m11
y M= ⎢
⎥
u 22 ⎦
⎣m21
⎡⎛
⎞
u12
m21 ⎟⎟
⎢ ⎜⎜ u11 .
m22
⎠ u12
⎢⎝
⎢
m11
m22
= ⎢
⎢ ⎛⎜ u . u 22 m ⎞⎟
21 ⎟
⎢ ⎜ 21 m
22
⎝
⎠ u 22
⎢
m11
m22
⎣⎢
0 ⎤
m22 ⎥⎦
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦⎥
(22)
En el caso de la industria 2, los coeficientes son los habituales
a12 = u12/m22 y a22 = u22/m22, pero en el de la industria 1, son distintos,
a saber:
a11 = (u12 -a12/m21)/ m11
(23)
y
a21 = (u21 -a22/m21)/ m11
(24)
90
Los coeficientes técnicos derivados en (23) y (24) son insumo neto
sobre producción neta de una industria, donde la producción neta es el
total de la producción industrial menos los productos secundarios, y
el insumo neto de una industria es igual al total de insumos menos el
insumo que requieren los productos secundarios producidos por esa
industria. Más importante aún, es que a partir de estas ecuaciones se
puede ver cuando los insumos requeridos para los productos secundarios se eliminan del total de insumos. Bajo esta perspectiva, el coeficiente técnico derivado puede ser negativo sí ocurre una de estas cosas:
1) Si hay exceso de especificación de los productos secundarios, es decir, la producción de productos secundarios en la
matriz de producción (el cuadro de oferta); en nuestro ejemplo, el producto 2 producido por la industria 1 está clasificado erróneamente;
2) El producto secundario no es exactamente el mismo que el
producto producido como primario en otras partes; necesita
menos insumo de lo que se supone.
3) Hay errores en los datos.
Haciendo uso de la tecnología de producción se puede generar coeficientes negativos pero, en lo económico, es posible explicarlos con
una de las razones mencionadas anteriormente. Es frecuente que un
insumo dado no sea necesario para una industria, pero si los productos
secundarios requieren este insumo, la eliminación de la producción
secundaria e insumos asociados por cierto generará un valor negativo
para el coeficiente técnico aij. La solución para el problema de los
coeficientes negativos es volver a verificar los datos. Los productos
secundarios significativos y sus insumos asociados deben transferirse
usando el método de la redefinición sobre la base de la información
proporcionada por los establecimientos que producen solamente este
tipo de productos secundarios o la reunida mediante encuestas especiales. Es necesario recalcar una vez más lo sugerido originalmente,
que en la medida de lo posible, los datos deben procesarse aplicando
91
reglas de separación y asignación de los costos en las fuentes, Naciones Unidas (2000, párr. 4.70).
Para los casos en que los coeficientes negativos sean muy pequeños en
comparación con los otros coeficientes de la misma columna, los especialistas los pueden equiparar a cero y equilibrar los cuadros aplicando
el Método RAS (véase el capítulo IX de las Naciones Unidas, 2000) y
Mun-Heng TOH (1995).
III.4.2.3 Evaluación de los dos supuestos
Existen firmes razones para apoyar el supuesto de tecnología de producción, la primera es que resulta plausible económicamente y la
segunda es que el supuesto satisface todos los criterios que se mencionan a continuación25:
a) Balance material: la producción total es igual al consumo
intermedio total más la demanda final;
b) Balance financiero: La ecuación de precios es válida para
cada industria cuando se aplica a los ingresos y los costos de
los productores;
c) Invarianza de escala: la matriz simétrica de coeficientes
derivada también es invariante ante un factor de escala, es
decir, si los insumos y la producción de una industria en las
matrices originales de utilización y producción se incrementan
en la misma proporción, es posible derivar la matriz de coeficientes.
d) Invarianza de precios: Si se aplica un nuevo precio base a
los datos, se obtiene la misma matriz simétrica de coeficientes de Insumo-Producto A.
25
Estos criterios han sido formulados en un documento de Pieter K. Cansen y Thies ten Raa,
“The choice of model in the construction of Input-Ouput coefficients matrixes”, International
Economic Review, Vol. 31, No 1, febrero de 1990. El documento original en el que se
señalarón por primera vez los problemas del supuesto de la tecnología es “An alternative
approach of negatives in Input-Output analisis”, Review of Economics and Stadistics, No
66 (1984) de Ties ten Raa, D. Charkraborty y J.A. citado por Naciones Unidas (2000).
92
Por otro lado, el supuesto de tecnología de la industria tiene dos claras
ventajas:
a) La matriz AI,cc siempre es positiva porque la matrices B y D siempre
son positivas y b) B y D pueden ser rectangulares y la matriz de producción A1 siempre es cuadrada. Sin embargo, este supuesto plantea
algunos problemas que harán rechazarlo; bajo esta perspectiva, se refleja en el hecho que distintos productos son producidos con las mismas estructuras de insumos de la industria en el que se producen, ello
carece de sentido desde el punto de vista económico. La razón radica
en que si dos productos cualesquiera que tienen los mismos costos
porque se los produce con la misma tecnología, estamos en presencia
de un mercado en que los precios se fijan siempre iguales a los costos
(esto es lo que se supone una economía de Insumo-Producto en un
mercado competitivo perfecto), por lo tanto, no es posible que tengan
precios diferentes y sólo se podrá cumplir por coincidencia.
Además de esto, el supuesto de la tecnología de industria exige que las
participaciones en el mercado sean constantes en el tiempo, algo que
no es realista. Por otro lado, la interacción entre este supuesto y las
participaciones en el mercado hacen que se violen tres importantes
criterios enunciados anteriormente, a excepción hecha del criterio del
balance material.
En este mismo orden de ideas, es conveniente anotar que las Naciones
Unidas (2000, párr. 4.78), se sugiere usar el método de la transferencia
negativa sin agregación para tratar subproductos exclusivos, el método de la redefinición en combinación con el supuesto de la tecnología
de la producción en caso de los productos secundarios ordinarios y el
método de la redefinición debe usarse en la medida en que se disponga
información adicional y específicamente en el caso de productos que
generan valores negativos grandes. Los negativos pequeños pueden
convertirse en ceros y las diferencias en las sumas de columnas y de
filas se arreglan equilibrando el cuadro. Si se usa el supuesto de la
tecnología de la industria para calcular la matriz simétrica de Insumo-
93
Producto, se sugiere emplear el método de la redefinición para transferir productos secundarios de valor significativo utilizando cabalmente
la información básica disponible antes de aplicarlo. Algunos
compiladores26 han argumentado el hecho en la cual una tecnología de
industrias es válida o no; en respuesta a esto es empírica y, por lo
tanto, no es posible excluirla sólo por consideraciones teóricas.
En coincidencia con lo planteado, Cortés y Pinzón (2001, p. 234),
recalcan que los diferentes métodos para adecuar las matrices InsumoProducto se derivan de los supuestos o hipótesis sobre el cual se apoyan,
por ejemplo: la tecnología del producto, la tecnología de la industria o
mixtas. Lo único es no dejar de lado en el análisis, la derivación en la
cual se sostiene el Modelo Insumo-Producto, es decir, la primera supone para un producto la misma estructura de costos sin importar la
rama que lo produce y la segunda asume diferentes estructuras de costo
de acuerdo con la rama origen.
26
Denmark Statistic, Commodity flow systems and construction of Input-Output tables in
Denmark, 1986, citado por Naciones Unidas (2000).
94
IV. ANÁLISIS TEÓRICO DEL MODELO INSUMO-PRODUCTO
(MIP) DE LEONTIEF
En este apartado, se pretende analizar el modelo teórico de InsumoProducto, evaluando la función de producción de Leontief y la forma
como ésta responde a los cambios en los factores productivos; bajo
esta perspectiva, se busca exponer la deducción analítica del modelo y
la relación entre la función microeconómica de Leontief y el modelo
macroeconómico de Insumo-Producto.
En este mismo orden de ideas, se expondrá los supuestos básicos del
MIP y el cálculo de la inversa de Leontief asociada a la corrección de
los productos secundarios. Por otro lado, es conveniente mencionar
las aplicaciones teóricas más relevantes del MIP en el análisis sectorial, concernientes a la determinación de empleo de los requerimientos
primarios de personal ocupado y formación bruta de capital, la determinación de los precios y la determinación de los sectores claves que
dinamizan una economía a partir de los índices de eslabonamientos
intersectoriales.
IV.1 Funciones de producción
Toda función de producción, asocia a cada conjunto de Inputs (servicios de los factores utilizados por período) el máximo Output o nivel
de producción por período alcanzable. En este sentido, Fernández y
Tugores (1991, p. 191), mencionan que la esencia de toda actividad
productiva, es obtener bienes y servicios con destino final al consumo,
utilizando recursos de la economía; esto hace referencia a diversos
elementos, como lo son los factores de producción (tierra, capital y
trabajo) y que las unidades de producción parten de aspectos como la
maximización de beneficios o la minimización de costos.
95
Visto desde esta perspectiva, el trabajo Amaya (1995, p. 3), identifica
la producción como cualquier actividad capaz de incrementar los bienes y servicios disponibles a través del uso de una determinada cantidad de insumos para generar el máximo nivel de producción. Esto puede
ser representado por una función de producción la cual requiere eficiencia técnica, es decir, sin la presencia de recursos factoriales ociosos; por lo tanto, la empresa debe elegir una combinación (InputsOutputs) que sea económicamente eficiente y cuyo costo sea lo más
bajo posible.
Por otro lado, se hace la distinción entre insumos fijos e insumos variables; el primero corresponde a aquella cantidad de insumos que no
varían durante el período de tiempo tomado en consideración, mientras que el segundo puede cambiar durante el período relevante de
tiempo. Bajo este enfoque, el corto plazo puede ser interpretado como
el período lo suficientemente corto de manera que al menos un insumo
es fijo y el largo plazo puede ser comprendido como un período lo
suficientemente largo como para que todos los insumos sean variables
(Amaya, 1995).
IV.2 Rendimientos de escala
Caracterizar las funciones de producción de la manera como éstas responden a los cambios en los factores productivos, es un concepto de
rendimientos de escala (Nicholson, 1995: p. 209). Si la función de
producción está dada por Q = f (K,L ) (1) y todos los factores se multiplican por una constante positiva m, (donde m >1) entonces, se clasifica los rendimientos de escala de la forma siguiente:
a) f(mK, mL) = mf(K,L) = mQ -------- rendimientos constante de escala
b) f(mK, mL) < mf(K,L) = mQ -------- rendimientos decrecientes de escala
c) f(mK, mL) > mf(K,L) = mQ -------- rendimientos crecientes de escala
96
En términos intuitivos, si un aumento proporcional de los factores eleva la producción en la misma proporción, la función de producción
muestra rendimientos constantes de escala; si la producción aumenta o
disminuye más que proporcionalmente ante aumentos proporcionales
en los factores de producción, estamos en presencia de rendimientos
crecientes y decrecientes, respectivamente.
IV.3 Función de Producción de Leontief
La función de Leontief, puede expresarse como una función de producción que registra la cantidad máxima del nivel de producción que
se puede generar con una cantidad mínima de insumos (Amaya, 1995:
p. 39), es decir, es una función de producción de proporciones fijas
(Varian, 1998). Esto puede ser representado de la siguiente manera:
Q = f ( K , L) = A min f K , L
(2)
El parámetro A, (A >0) nos indica el estado de la tecnología.
Esta función implica que:
(3)
Q = f ( K , L) = A K si K < L
A L si K > L
La función de Leontief (3), en ambos caso satisface la propiedad
f(0)=0 y f(K,L) • 0 en V(x)27. Además, la función f es continua en la
región superior e inferior y linealmente homogénea. En este sentido, si
multiplicamos cada factor de producción por una constante y el producto Q estará multiplicado por esa constante, indica que la función de
Leontief presenta rendimientos constantes a escala; también es bueno
27
V(x) es designado como el conjunto de insumos requeridos, es decir, el conjunto de todas
las combinaciones de insumos que producen al menos x unidades de producto. Esto es:
V(x) ={y ∈ IR+n : (x, y) esta / enX} X es el nivel de producto.
97
mencionar, que esta función no permite sustitución entre los insumos,
es decir, presenta elasticidad de sustitución cero.
Para Jones (1988, p. 30), “la cantidad de output producido por una
economía está limitada por la oferta disponible de capital y trabajo”.
Lo que interesa destacar es que la función de producción de Leontief
es una función de coeficientes fijos, es decir, si partimos de (1), la
relación de producción agregada Q, se determina en proporción directa a las cantidades de capital y trabajo, por lo tanto;
Q = K/v o L/u
(4)
donde v y u son constantes.
Esta forma de relación de producción supone básicamente un
Q = min K / v, L / u (5)
Este tipo de tecnología implica la inexistencia de sustitución entre capital y trabajo para la producción del Output y dada cierta cantidad de
capital, solamente se puede producir un único flujo de Q, aunque haya
más trabajo disponible.
El supuesto de rendimientos constantes a escala permite llevar a cabo
una simplificación sustancial de la función de producción agregada
que puede expresarse de forma per cápita.
Si dividimos la función de Leontief (1) entre el factor trabajo y
obtenemos:
Q/L = f(K/L,1)
(6)
(6) indica simplemente que el producto por trabajador depende del
capital por trabajador, o relación capital trabajo
k = K/L
(7)
98
Así obtenemos:
q = f (k,1) (8) La función de producción agregada por trabajador (Jones,
1988).
En este mismo orden de ideas, la función de Leontief indica la existencia de una sola manera eficiente de generar un determinado producto
(Amaya, 1995: p.40). Esto es:
Xj =Q = min xij/aij (j = 1,2,…,n)
(9)
Xj representa el producto total del sector j, xij la cantidad de bienes y
servicios producidos por el sector i y consumidos por el sector j y aij la
cantidad de producto del sector i necesaria para la producción de una
unidad de producto por parte del sector j, aij es denominado el coeficiente técnico de Insumo-Producto, que expresa las relaciones entre
los insumos y el producto de determinado sector o industria.
Visto de esta forma y pocas palabras, la función de producción de
Leontief, opera bajo rendimientos constantes a escala e inexistencia
de sustitución entre los insumos, por consiguiente, así se generan los
supuestos básicos de soporte para el análisis Insumo-Producto.
IV.4 Modelo Matricial Insumo-Producto
El modelo Insumo-Producto es un conjunto de ecuaciones lineales,
que busca mostrar las interrelaciones e interdependencias existentes
entre los sectores y actividades económicas (Sonis y Hewings, 2000),
por ello parte del desarrollo teórico de la función de producción
microeconómica de Leontief (1) para el desarrollo macroeconómico
del modelo Insumo-Producto. Además, “se omiten las funciones de
utilidad y las demandas de los consumidores se tratan como variables
exógenas sin tener en cuenta de manera explícita el equilibrio de los
99
consumidores” (La unidad de producción homogénea no es la empresa
sino la industria, Herderson y Quant, 1992, p. 443).
Dentro de este orden de ideas, el modelo matricial Insumo-Producto
permite estudiar el comportamiento de los sectores productivos que
demandan bienes y servicios para su producción o la demanda final,
también insumen factores de producción y otros productos para llevar
cabo su proceso productivo, y en este sentido, hace uso de un sistema
de ecuaciones lineales para determinar empíricamente sus parámetros
o coeficientes técnicos.
Para establecer el sistema Insumo-Producto se debe mencionar los tres
supuestos básicos que se basa en la naturaleza de la producción28:
1) Cada industria o sector produce un sólo tipo de mercancía. Esto
determina un sólo método de producción para las mismas, por lo
tanto un producto x elaborado mediante n procesos distintos será
considerado como n- bienes diferentes y si no existe sustitución
entre los productos entre los sectores. Este supuesto se denomina
Homogeneidad.
2) Los insumos usados por cada sector sólo son función lineal de su
nivel de producción, por lo tanto esta cantidad de insumos varía
en la misma proporción que la producción, en consecuencia no
indica que estamos en presencia de rendimientos constantes a
escala. Este supuesto se denomina Proporcionalidad.
3) El efecto total de la producción en varios sectores será es igual a
la sumatoria de los diferentes efectos, entonces, estamos en presencia del supuesto de la Aditividad.
En general, la Homogeneidad exige que todos los productos de un
sólo sector o industria se produzcan en proporciones fijas bajo una
estructura única de insumos y sin sustitución automática entre los productos de los diferentes sectores, la Proporcionalidad muestra que los
insumos utilizados por una industria varían en proporción directa a las
variaciones de su producción total y Aditividad excluye toda interde28
Tomado del Modelo Insumo-Producto de Leontief por Angélica Amaya, 1995, p. 44.
100
pendencia externa de los sectores excepto la especificada en el modelo Insumo-Producto.
Por otro lado, Chiang (1987), Herderson y Quant (1992) y Amaya
(1995) coinciden en que el Modelo Insumo-Producto son un conjunto
de ecuaciones lineales cuyo objeto consiste en dar solución a la nincógnitas que representan los niveles de producción de los sectores
productivos en función de las demandas finales que se supone conocida (exógena), bajo la presencia de economías de escala y la no existencia de shocks tecnológicos; en efecto de allí se da a conocer la
relación e interdependencia entre los sectores productivos.
IV.4.1 Deducción Analítica del MIP
Partiendo del agente microeconómico o la función de Leontief de un
sector (9), se puede observar la distribución del producto del sector i
en el Modelo Insumo-Producto puede ser representada de la siguiente
manera:
n
Xi = ∑ Xij + Yi (10) expresa el valor bruto de produción (VBP) o proj=1
ducción total como la suma de la demanda intermedia y la demanda
final.
n
∑ Xij Es el consumo intermedio, que son todos aquellos bienes y servicios
j=1
que se adquieren para ser insumidos para el proceso de generación de
bienes finales y Yi representa el consumo final de bienes y servicios
que se adquieren para satisfacer sus necesidades de consumo final,
formación de capital y en definitiva la demanda final.
La característica principal del modelo Insumo-Producto es que permite
calcular la estructura de los coeficientes técnicos, que o es más que lo
producido por i para j para producir una unidad de su producto
Xij
aij =
(11)
Xj
101
X11 + X12 + X13 + ….. + X1n + Y1 = X1
X21 + X22 + X23 + ….. + X2n + Y2 = X2
X31 + X32 + X33 + ….. + X3n + Y3 = X3
(12)
…………………………………………..
Xn1 + Xn2 + Xn3 + ….. + Xnn + Y4 = Xn
El MIP trabaja con la hipótesis central, de que la producción del sector
i utilizada por el sector j es proporcional a la producción del sector j,
esto se expresa:
Xij = aijXj Siendo el coeficiente de proporcionalidad el coeficiente
técnico de la producción.
a11X11 + a12X12 + a13X13 + ….. + a1nX1n + Y1 = X1
a21X21 + a22X22 + a23X23 + ….. + a2nX2n + Y2 = X2
a31X31 + a32X32 + a33X33 + ….. + a3nX3n + Y3 = X3
(13)
…………………………………………..
an1Xn1 + an2Xn2 + an3Xn3 + ….. + annXnn + Yn = Xn
En términos matriciales (12) puede ser escrita como:
()(
X1
X11
X12 X13 ….. X1n
X2
X21
X22 X23 ….. X2n
X3 =
X31 X32 X33 ….. X3n
Xn
)( ) ( )
1
+
Y1
1
+
Y2
1
+
Y3
………………………………………..
Xn1
Xn2 Xn3 ….. Xnn
1
+
Yn
Por el lado de las compras o columnas, se muestra los desembolsos
efectuados por la industria o el sector j en insumos intermedios,
bienes importados y de insumos importados:
102
n
Xj = ∑ + Xij + Mj + VABj
(14)
i=1
Mj y VABj son los vectores de importaciones del producto del sector j
y su respectivo valor agregado bruto. La apertura del valor agregado
representa como se genera el ingreso de los sectores productivos y
junto a las importaciones representan pagos, mientras que los Xij
representa la demanda o compras de insumos primarios que también
puede darse el caso de la existencia de sectores que use insumos propios para llevar a cabo su proceso productivo.
X1 = X11 + X12 + X13 + ….. + X1n + VAB1 + M1
X2 = X21 + X22 + X23 + ….. + X2n + VAB2 + M2
X3 = X31 + X32 + X33 + ….. + X3n + VAB3 + M4
………………………………………
Xn = Xn1 + Xn2 + Xn3 + ….. + Xnn + VABn + Mn
En términos matriciales (14) puede ser escrita como:
() (
X1
X11
X12 X13 ….. X1n
X2
X21
X22 X23 ….. X2n
X31
X32 X33 ….. X3n
X3
=
)( ) ( )( )
1
VAB1
M1
1
VAB2
M2
1 +
VAB3 + M4
……………………………………
Xn
Xn1
Xn2 + Xn3 ….. Xnn
..
1
VABn
Mn
La producción total de la economía está dado por:
n
X = ∑ Xj + C + G + I + E (15) donde C, G, I, E, son los componentes
j=1
de la demanda final o demanda agregada como las compras hechas por
los hogares, el gobierno, la inversión y las ventas de bienes y servicios
al extranjero.
103
n
También la producción total puede obtenerse como: X = ∑ Xj+ M +
j=1
VAB (14) partiendo de (14) y (15) y del hecho que la oferta total es igual
n
n
n
n
a la demanda total y ∑ Xj = ∑ Xj entonces; ∑ Xi + M + VAB = ∑ Xj+
j=1
j=1
j=1
j=1
C+G+I+E
Así obtenemos, VAB = C + G + I + E – M PIB (16), esta serie de
variables y sus interrelaciones pueden ser obtenidas en el MIP. Por
consiguiente, este modelo permite mostrar las principales variables
macroeconómicas usadas en la planificación económica y de igual
manera, es una herramienta que permite estudiar las interdependencias
sectoriales o industriales de una economía.
Esto muestra una clara relación entre los sectores productivos (véase
Cuadro 2), el Cuadrante I muestra la el comportamiento del consumo
intermedio Xij, cada elemento representa la cantidad de bienes y servicios producidos por el sector i, que es insumido por el sector j para
llevar a cado su proceso productivo y unos de los cuadrantes más importantes para una economía ya que es la matriz de costos intermedios
parte fundamental de las cuentas interindustriales. El Cuadrante II representa los componentes de la demanda agregada la cual está dividido en Consumo Privado (C), Consumo de Gobierno o Publico (G),
Inversión (I) y Exportaciones (E).
El Cuadrante III contiene Las Importaciones (M) y todos los elementos de la cuenta de generación del ingreso, en otras palabras la distribución del Valor Agregado Bruto (VAB) en las Remuneraciones de
Empleados y Obreros (REO), Impuestos sobre los productos netos
(TIN), el Consumo de capital fijo (CCF), el Excedente de Explotación
(EE). Por último, el Cuadrante IV contiene los insumos primarios utilizados por los sectores que componen la demanda final y también
suele ser usado para el cálculo de diferencias computacionales asignada a las variaciones de existencias.
104
Las filas del MIP indican la distribución de los bienes o servicios producidos de una determinada industria y las columnas son los orígenes
de los insumos necesarios para llevar a cabo el proceso productivo.
Por otro lado, las tablas Insumo-Producto nos proporcionan una visión
detallada del proceso de la producción, por otro lado, al existir un
cambio en las variables de demanda agregada se puede estimar cuál
será el comportamiento de la producción. Este proceso estará explicado por los coeficientes de los requerimientos técnicos aij que indican
la cantidad de producto del sector i que será necesaria para la producción de una unidad de producto del sector j29, estos coeficientes son
también llamados coeficientes de Insumos-Productos directos, asumidos constantes.
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
○
Cuadro 2
EJEMPLO DE LA MATRIZ INSUMO-PRODUCTO
1
2
3
4
5
…
n
C
I
E
DF
Xj
1
C1
I1
E1
Y1
X1
2
C2
I2
E2
Y2
X2
3
C3
I3
E3
Y3
X3
C4
I4
E4
Y4
X4
C5
I5
E5
Y5
X5
I
Xij
4
…
…
…
…
…
…
5
II
n
Cn
In
En
Yn
Xn
IM
M
M1
M2
M3
REO
REO1
REO2
REO3
M4
M5
…
Mn
CM
…
REOn
REOM
TIN
TIN1
TIN2
III TIN3
TIN4
TIN5
…
TINn
CCF
CCF1
CCF2
CCF3
CCF4
EE
EE1
EE2
EE3
EE4
CCF5
…
CCFn
CCFT
EE5
…
EEn
EE
X1
X2
X3
X4
X5
---
Xn
REO4 REO5
MT
REOT
IV
CT
IT
TINT
ET
YT
YT
Notación:
Xij es lo producido por el bien por el sector o la industria i que es usado como insumo por el sector o la industria j.
29
Ecuación (2).
105
Yi
Es la demanda final, en donde se encuentran los productos para
la demanda agregada o absorbidos por la demanda final ( C, G,
E, I)
Xi
Es el total de la producción del sector i
Xj
Insumos Totales
M
Importaciones
REO
Remuneraciones a empleados y obreros
I
Inversión
E
Exportaciones
CCF
Consumo de Capital Fijo
TIN
Impuestos Indirectos Netos sobre la producción.
EE
Excedente de Explotación
Reordenando la ecuación (12)
X1 - a11X1 - a12X2 - a13X3 - ….. - a1nXn = Y1
X2 - a21X1 - a22X2 - a23X3 - ….. - a2nXn = Y2
X3 - a31X1 - a32X2 - a33X3 - ….. - a3nXn = Y3
(17)
………………………………………
Xn - an1X1 - an2X2 - an3X3 - ….. - annXn = Yn
Luego asociamos los términos X1’s en la primera ecuación y los X2’s en
la segunda ecuación y así sucesivamente:
(1 - a11)X1 - a12X2 - a13X3 - ….. - a1nXn
= Y1
- a21X1 +(1- a22)X2 - a23X3 - ….. - a2nXn
= Y2
- a31X1 - a32X2 + (1-a33)X3 - ….. - a3nXn
= Y3
………………………………………….
Xn - an1X1 - an2X2 - an3X3 - …..+(1- ann)Xn = Yn
106
(18)
En forma matricial podemos rescribir (18)
A=
a11
a12
a13
...
a1n
a 21
a 22
a 23
...
a2n
a31
.
a32
.
a34
.
...
...
a3n
.
a n1
an2
an3
...
a nn
X1
○
○
X2
○
○
Y1
Y2
, X = X 3 , Y = Y3
...
...
Xn
Yn
Por otra parte sea I, la matriz identidad n x n, entonces expresamos
(18) como:
(I-A) X = Y (19); la matriz A no es más que la matriz de coeficientes
técnicos o de de requerimientos directos de insumos y cuyos subíndices
permiten ubicar su posición en la matriz.
Por otro lado, la matriz I-A es no singular, es decir, su determinante es
diferente de cero Det. (I-A) • 0, lo que entonces existe su inversa
(I-A)-1 y como resultado se obtiene;
(I-A)-1 Y = X
(20)
La matriz (I-A)-1 se denomina la matriz inversa de Leontief y si denotamos por rij cada uno de los elementos de esta matriz denominados los
coeficientes de requerimientos directos e indirectos, cuyo significado
es la cantidad de bienes y servicios del sector i requeridos por el sector
j, necesarios para satisfacer una unidad de su demanda final.
V.4.2 Cálculo de la Matriz Insumo-Producto Inversa
La inversa de Leontief, o matriz de requerimientos directos e indirectos debe estar asociada estrechamente a lo que se denomina homogeneidad de la función de producción, es decir, debe ser obtenida sin la
presencia de productos secundarios; bajo esta perspectiva, en la diagonal principal encontramos los requerimientos directos y fuera de ella
(diagonal superior e inferior) se ubican los requerimientos indirectos.
107
Partiendo de la ecuación (10).
n
Xi = ∑ Xij + Yi que expresa el valor bruto de producción como la suma
j=1
de la demanda intermedia y la demanda final y esta será igual a Xj de la
ecuación (14).
Por otro lado, como (11) es igual a, aij =
coeficientes técnicos es igual a ([aij]) = A.
Xij
Xj
entonces la matriz de
Según lo descrito anteriormente, encontramos que (10) es igual a:
Xi = A Xi + Yi donde A es la matriz de coeficientes técnicos.
Si se despeja matricialmente Xi se obtiene:
(I-A)-1 Yi = Xi (20) que es igual a la ecuación
(21)
En este sentido, (I - A)-1 es la matriz de coeficientes de requisitos totales, directos e indirectos [rij]. Por ejemplo, r12 es la producción de
sector “1” que requiere el sector “2” para satisfacer una unidad adicional de demanda final, por lo tanto, esta es la matriz inversa de Leontief
que evaluar impactos sobre la producción de variaciones en la demanda final.
La presencia de producción secundaria en las actividades o sectores
productores de bienes y servicios, es normal en cualquiera economía.
Esto hace que los coeficientes deducidos técnicos calculados en el
modelo sean espurios o distorsionados.
Para superar el problema anterior y revisando el capítulo III sobre el
tratamiento de los productos secundarios, se puede definir dos matrices obtenidas a partir de la cuadros de oferta y utilización (COU): una
de producción V y otra de utilización o absorción U. Con las matrices
108
V y U se establece una distinción entre la producción bruta por producto y la producción bruta por actividad que en el modelo a partir de las
ecuaciones (10) y (14) se supone iguales.
En este caso, es necesario la construcción de una matriz que permita
relacionar el VBP que es igual Xi con la demanda final por medio de la
relación (14), no es tan simple, es necesario establecer una hipótesis
sobre la tecnología de producción (método matemático), para la corrección de la producción secundaria.
Las dos opciones más frecuentes, señaladas en el capítulo III son:
• Tecnología de Industria
Ésta supone que para obtener un producto en una actividad, todos los
insumos se utilizan en la misma proporción, por ejemplo, si evaluamos
los insumos requeridos por el producto 1, son:
Actividad 1 Actividad 2
Insumo 1, producto 1:
a11 = b11. d11 + b12. d21+.....
Insumo 2, producto 1:
a21 = b21. d11 + b22. d21+.....
(22)
n = insumos y m = productos
d11 =
proporción de la actividad 1, en la producción de 1 (fija para
todos los insumos).
d21 =
proporción de la actividad 2, en la producción de 1 (fija para
todos los insumos).
b11 =
insumo 1, que necesita la actividad 1, para producir una unidad
de producto 1.
b21 =
insumo 2, que necesita la actividad 1, para producir una unidad
de producto 1.
109
• Tecnología de Productos
Aquí se supone, que en la elaboración de un producto, se usa la misma
proporción de un insumo, independientemente de la rama de actividad
donde se realiza su producción, por ejemplo, el insumo 1 requerido
por cada actividad es:
Producto 1 Producto 2
Insumo 1, requerido por la actividad 1: u11 = a11.m11 + a12 .m12 +….. (23)
Insumo 1, requerido por la actividad 2: u12 = a11.m21 + a12 .m22 +…..
a11 =
Insumo1, requerido para producir una unidad del producto 1
(fija para todos las actividades o sectores)
a12 =
Insumo1, requerido para producir una unidad del producto 2
(fija para todos las actividades o sectores)
m11 =
Producción del producto 1, por la actividad o sector 1
m21 =
Producción del producto 1, por la actividad o sector 2
Bajo las hipótesis anteriores y en concordancia con la conversión de la
Oferta total y Demanda Total a precios básicos, las Naciones Unidas
(2000), el Banco Central de Chile (1996) y el Instituto Nacional de
Estadística e Informática de Perú (2001) coinciden que en ambos casos conviene utilizar las tablas valoradas a precios básicos, dado que
así, se obtienen los coeficientes técnicos más depurados, exentos de
márgenes de distribución e impuestos indirectos.
• Solución con la Hipótesis de Tecnología de Industria usada para el
cálculo de la inversa del MIP.
Esta es una de las hipótesis de mayor uso en los nuevos enfoques de
construcción de los modelos Insumo-Producto al presentar características que hacen más directa su aplicación, el Banco Central de Chile
(1996) e Instituto Nacional de Estadística e Informática de Perú (2001)
trabajaron con esta hipótesis, aunque puede ser discutible la validez
económica de sus supuestos. Las ventajas de las hipótesis de la tecnología de industria son:
110
√
√
Siempre entrega coeficientes técnicos positivos.
Se puede aplicar a tablas de producción rectangular, donde
difiere el número de productos y actividades.
Por otro lado, plantear una solución con la Hipótesis de Tecnología del
Producto, tiende a dar como resultado coeficientes negativos, la cual
tendrían que reajustarse por el método RAS o regresar a la máxima
apertura y utilizar métodos manuales como la redefinición, lo que genera
grandes inversiones de tiempo y de revisiones en aquellos productos
donde el coeficiente técnico es o son negativos y así luego hacer las
estimaciones de la matriz de costos, a pesar que entre ambas hipótesis
las diferencias entre coeficientes pueden ser marginales.
La nueva matriz de coeficientes técnicos deducida de la hipótesis adoptada es:
A=
D x B donde:
B=
U. -1 (matriz de coeficientes técnicos, producto x actividades)
D=
V’. -1 (matriz de participación en el mercado por actividades)
U:
Matriz de Consumo Intermedio (absorción) (m productos x
n actividades)
V:
Matriz de producción (oferta) (m productos x n actividades)
g:
Vector columna de producción intermedia por actividad (n x 1)
(suma por columna de la matriz V = VBP= Xi)
q:
Vector columna de producción por producto (m x 1) (suma por
fila de la matriz V =VBP) (oferta nacional).
^
g:
Matriz diagonal con la producción intermedia por actividad
(n x n)
^
q:
Matriz diagonal con la producción por producto ( m x m).
111
Se tienen las siguientes igualdades:
n
9q = Bg + Yi (que corresponde a VBP = ∑ Xij + Yi = Xi (1) ) (24)
j=1
9
g = Dq
(25)
Reordenando las dos ecuaciones anteriores se obtiene:
q = BDq + Yi
(26)
(I - BD)-1Yi= q (*)
(27)
Entonces, la matriz de requisitos totales, “producto x producto”, es:
(I -A) -1 = (I - BD)-1
(28)
Por último, la siguiente ecuación permite relacionar la producción
y demanda intermedia:
(I - DB)-1Yi= g (**) donde (I-DB)-1 es la matriz de requisitos totales
directos e indirectos “Actividad x Actividad”, que será igual a la matriz (I-A)-1 de modelo teórico de Insumo-Producto.
IV.4.3 Determinación del empleo
La determinación del empleo en un MIP cosiste en determinar los requerimientos de factores primarios por industrias o sectores productivos y unidad de demanda final. Bajo los supuesto de la existencia del
uso de ciertas cantidades de trabajo, capital y factores interindustriales
y en la cual existe una perfecta elasticidad precio de la oferta de insumos primarios (Puentes, 1993; p. 21).
Sea:
F1= F12 + F12 + F13 + ........ + F1n
F2= F21 + F22 + F23 +........ + F2n
(29)
F1 y F2 representan el uso total de capital y trabajo, respectivamente,
mientras cada Fij son las cantidades de capital o trabajo requeridos por
dichos sectores.
112
Los coeficientes primarios se observan en la ecuación
fij = Fij / Xj
(30)
i,j = (1,2,3......)
Expresamos ahora los coeficientes en forma matricial:
f=
[
f11
f12
f13
...
f1n
f21
f22
f23
...
f2n
]
donde el elemento f1j, es el capital requerido para producir una unidad
de producto, en el sector j, y f2j, son las cantidades de trabajo requerido
para producir una unidad de producto en el sector j.
Si reemplazamos en (29) los Fij por fij *Xj , nos quedaría de la
siguiente manera:
F1= f12 X1 + f12 X2 + f13 X3 + …….. + f1n Xn
F2= f21 X1 + f22 X2 + f23 X3 +…….. + f2n Xn
(31)
Ahora en forma matricial: F = f*X y sustituyendo en esta la
ecuación (21)
(I-A)-1 Y = X resulta:
F = f*(I-A)-1 Y
(32)
La ecuación (32), muestra que el vector de requerimientos de factores
de producción (capital, trabajo) puede ser expresado como una función de la demanda final, lo que implica que la matriz de requerimiento
de factores sea postmultiplicada por la inversa de la matriz de Leontief.
113
Además, podemos determinar, mediante el análisis estático comparativo del modelo, los cambios en los requerimientos de insumos primarios (trabajo y capital), ante variaciones de la demanda final30.
Por otro lado, debido a que el COU muestra la Formación Bruta de
Capital y el Personal Ocupado asociado a cada Actividad y en nuestro
modelo una vez que corregimos la producción secundaria tenemos una
matriz producto por producto, entonces para poder operar y observar
como cambios en la demanda final reordenan los requerimientos de
capital y trabajo dentro del modelo Insumo-Producto.
La primera ecuación utilizada para obtener la FBK y el PO asociado a
cada producto es un vector de coeficiente de producción total actividad por producto, por otro lado, la matriz de transacciones debe estar
ajustada a una matriz de coeficientes técnicos “pura”, es decir, sin
producción secundaria. Esta matriz “pura” de coeficientes técnicos
permitirá obtener valores más acertados para los multiplicadores de
requerimientos de Personal Ocupado y Formación Bruta de Capital.
Se plantea una nueva ecuación (33) para obtener una matriz pura de
coeficientes técnicos.
D = Vt. q^-1 (33) (matriz de participación de la producción de cada
actividad en el total del mercado)
Se traspone la ecuación (33)
Dt = (Vt. q^ -1)’
30
(34)
Véase para la ampliación del modelo, el texto de: Zbifniew Kozihowski, Ítems, Cap. 8,
página 150-166. Citado por Puentes, Rodolfo (1993).
114
Los coeficientes primarios se observan en la ecuación (30)
fij = Fij / Xj
f=
[
i,j = (1,2,3......) está asociado a cada actividad
f11
f12
f13
...
f1n
f21
f22
f23
...
f2n
]
Ahora multiplicamos (30) y (34) matricialmente
f * D’ = f1 (19) son los requerimientos unitarios de PO y FBK asociados a la tecnología de la industria y por lo tanto están asociados a los
productos y no a las actividades.
Por último la ecuación (32) teórica se sustituye (19) y la inversa (I - BD)-1
Di F = f*(I-A)-1 Y =
(32)
F1 = f1*(I - BD)-1Y
(35)
La ecuación (35), muestra que el vector de requerimientos de factores
de producción (capital, trabajo) puede ser expresado como una función de la demanda final, lo que implica que la matriz de requerimiento
de factores asociada a los productos sea postmultiplicada por la inversa de la matriz de Leontief producto por producto31. Dentro de este
marco, ampliaciones de lo expresado anteriormente se pueden observar en trabajos como los de De Tarso (2002) que consiste en observar
la relación entre los cambios tecnológicos y la generación de empleo,
con la ayuda de un Modelo de Insumo-Producto (MIP) de Leontief,
para asociar las políticas de empleo con las políticas de desarrollo
tecnológico.
31
Hipótesis de tecnología de la industria.
115
Por otro lado, el nivel de actividad económica, constituye el determinante más general de la demanda de trabajo, tanto en el ámbito global
como sectorialmente, de esta manera una de las manifestaciones más
importante, es que la modificación en la capacidad de producción por
ocupado en cada sector, ya sea por innovación tecnológica, por intensificación de trabajo cambia los requerimientos de empleo por unidad
de producto (Mariña; 1995).
IV.4.4 Determinación de precios
El hecho que las tablas Insumo-Producto son construidas en unidades
monetarias, pues no es fácil obtenerlas en unidades físicas o en términos constantes. Sin embargo, conociéndose el vector de precios puede
hallarse matrices Insumo-Producto a valores corrientes a partir de
matrices a precios constantes (unidades físicas) o viceversa (Amaya,
1995, p. 52).
Si partimos de la ecuación (3) para el sector i
Xi = Xi1 + Xi2 + Xi3 + ..... + Xin + Yi
(36)
Suponiéndose que el vector de precios es conocido, Pi (i = 1,2,3,.....,,n)
Entoces las variables en unidades físicas y monetarias están dadas por:
Qi = Pi Xi ; qij = Pi Xij ; Di = Pi Yi
(37)
Qi representa el valor bruto de producción en términos corrientes sector i, qij es el valor del consumo intermedio del sector i y Di el valor de
la demanda final. Entonces reescribiendo (36)
n
Qi = Pi Xi = ∑ qij + Di
(38)
i=1
~
Ahora, en forma matricial Q = [Qi] , Qi = [qij] y D = [Di], entonces
116
~
Q = Qi +D (39) y las cantidades están expresadas en las mismas
unidades monetarias y por ello se pueden recalcular la oferta y la utilización de la producción.
Bajo los supuestos de que los precios del los factores de producción
primarios (K,L) y la incorporación de los precios no altera el hecho de
la permanencia de los rendimientos constantes, para cada sector productivo.
Ya habiendo calculado los requerimientos de capital y trabajo por unidad
de producción para cada unos de los factores productivos, es necesario
determinar los costos de producción. Amaya (1995, p.53) manifiesta
que el sistema de precios se basa en la premisa de que el costo de cada
producto esta formado por las compras de insumos realizadas a otras
industrias y los costos primarios directos. Por consiguiente, los costos
de producción {Cj} se obtienen al multiplicar los elementos de la columna de insumos primarios por los respectivos precios y se suman
estos parciales para obtener el total.
a1jP1 + a2jP2 + a3jP3 + ….. + a1jPn + f1j W1 + f1j W1 + f1j W1 + ….. + f1j W1
+
f2j W2
+
f2j W2 + f2j W2 +…….. + f2j W2
= Cj
(40)
j = (1, 2, 3, …, n)
Los aij representan los coeficientes de insumos directos, por otro lado
W1 y W2 son los precios del capital y el trabajo, respectivamente.
Puentes (1993; p. 28) recalca que “como en una economía competitiva, se eliminan las utilidades en todos los sectores productivos”, esto
implica que el precio de una mercancía (Pj) no puede exceder el costo
medio de producción {Cj}, por lo que se deduce que dicho precio es
igual a la ecuación (20).
117
n
n
i=1
k=1
Consolidando (40): Pj =∑ aij Pi +∑ fkj Wk para j = (1, 2, 3, …, n)
Expresando matricialmente lo anterior tenemos:
2
P1
a11 a12 a13 ... a1n
P2
a21 a22 a23 ... a2 n
P3 = a31 a32 a34 ... a3n
.
.
Pn
.
.
...
.
an1 an 2 an3 ... ann
∑ f k1Wk
k =1
P1
2
∑ f k 2Wk
P2
k =1
P3 + 2
∑ f k 3Wk
.
k =1
Pn
.
2
∑ f knWk
k =1
Es decir:
P = AtP + Z (42) At es la transpuesta de la matriz de coeficientes técnicos directos A y Z el vector de los costos de capital y trabajo asociados
a cada sector productivo.
Reagrupando y factorizando P se tiene:
(I- At)P = Z
(43)
Pre-multiplicando ambos miembro por la matriz inversa de Leontief,
(44)
se obtiene: (I- At)-1 (I- At)P = (I- At)-1 Z
P = (I- At)-1 Z (45) y como (I- At)-1 es la matriz de coeficientes de
requisitos totales, directos e indirectos = R y se deduce:
P = R*Z (46) en la cual cada precio es la multiplicación de matriz
inversa de Leontief por el renglón del valor de los coeficientes de insumos primarios, por consiguiente, el vector de precios es
n
n
i=1
k=1
Pj = ∑ (rij ∑ fk j Wk ) para j = (1, 2, 3, …, n)
118
(47)
Bajo esta perspectiva, Iveplan (1993) señala que con el Insumo-Producto se pueden estimar los efectos directos e indirectos de un cambio
en los precios de un sector sobre el resto de las actividades económicas, y de esta manera determinar las repercusiones sobre la economía
nacional. Por otro lado, Sáez (1992) manifiesta que un shock de costos
de los factores primarios afecta los precios y cantidades de equilibrio
de cada industria, por lo tanto haciendo uso del modelo Insumo-Producto se pueden repartir linealmente estos efectos inflacionarios y de
igual manera, Bulmer-Thomas (1982) menciona la necesidad de determinar los precios de eficiencia como un mecanismo para entender mejor
los impactos intersectoriales de variaciones de la demanda final, variaciones de los precios de intercambio y cambios en los costos factoriales.
IV.4.5 Determinación de los sectores claves
Unos de los aportes importantes que se genera al contar con matrices
Insumo-Producto es la determinación y visualización de los sectores
claves o prioritarios de una economía Fernández (1994, p. 35) muestra
que la hora de determinar los sectores de relevancia en la planificación
sectorial se necesita una identificación empírica de los sectores claves,
siendo el concepto de eslabonamientos (encadenamientos) un concepto
de considerable interés en la identificación de estos como estrategia de
desarrollo económico. También García y Ramos (2)(2003) menciona
que el análisis de los eslabonamientos permite determinar las características estructurales de los sectores estratégicos.
Estos sectores claves o estratégicos son los sectores que poseen un
mayor encadenamiento con el resto de los sectores dentro de una economía y “se ha creído que si los recursos (especialmente capital y la
habilidad empresarial) pueden ser concentrados en estos sectores claves,
el producto y el empleo en el país o región crecerá más rápidamente
que si estos recursos fueran distribuidos alternativamente”. (Fernández:
1994, p. 36).
119
La idea de utilizar los eslabonamientos como identificadores de los
sectores claves fue discutida por Hirschman (1968) citado por
McGilvray (1977, p. 51), en la cual identificó dos características que
rigen las economías en desarrollo: a) imperfecciones en el mercados
de bienes y factores y b) escasez de talento empresarial, en este mismo
orden de ideas, hay que reconocer que los recursos no se distribuyen
en forma centralizada, sino que dependen de las respuestas de azar de
los empresarios trayendo como consecuencias fallos de mercado en la
pérdida de oportunidades de inversión e incrementos en las importaciones producto de expansiones en la demanda agregada.
Hirschman (1968) citado por McGilvray (1977, p. 53) sostiene que
este proceso de identificación de los sectores claves, juegan un papel
importante en la creación de externalidades y desequilibrios, creando
mecanismos de señales en el mercado que marcan las oportunidades
de inversión. Fernández (1994, p. 37) enfatiza que el eslabonamiento
hacia atrás, los sectores claves requieren insumos de otros sectores
por encima del promedio, por consiguiente, existe una alta probabilidad de inversión en los sectores oferentes (expandir la producción de
bienes para el consumo intermedio y/o un mecanismo de protección de
los sectores nacionales y sustitución de las importaciones). Con respecto al eslabonamiento hacia adelante, es mecanismo es menos directo pero depende de la probabilidad de inversión en sectores en los
cuales el producto del sector estratégico sea insumo importante (Ej.: la
abundante fibra de algodón como producto que ejerce un efecto expansivo en la producción en textiles de fibra); entonces, al estimular la
producción en un sector clave, ampliará la posibilidad de incrementar
la inversión hacia un activo proceso de crecimiento.
Para determinar los sectores claves de una economía, es contar con un
índice que recoja los efectos directos e indirectos de cambios de la
demanda final y que permita observar cuáles son los sectores que absorben estos choques, por consiguiente, estos serán los sectores que
dinamizarán el circuito económico desde el punto de vista de la producción y el consumo intermedio.
120
Fuentes y Sastre (2001) mencionan que hay que desarrollar estrategias
a corto y largo plazo, en esta estrategia el sector clave está desempeñando un papel fundamental, y su concepto se ha entendido de diversas maneras. Primero dicha conceptualización clasifica los sectores
claves de manera muy general, como actividades económicas: primarias, secundarias y terciarias. Segundo, lo definen como complejos industriales que presentan fuertes dinamismos y relaciones iterativas.
Tercero, son sectores polarizados o enclaves, caracterizados por estar
altamente interrelacionados de manera circular. Cuarto. Son aquellos
sectores líderes, de gran dinamismo pero de escasa relación con el
resto de la economía. Así se ha verificado, que hay que tomar en cuenta la forma como definimos los sectores claves, a la hora de proponer
políticas y estrategias para el desarrollo, en la cual, estos sectores sean
los ejes de las estrategias.
Los índices que realmente consideran tanto los efectos directos como
indirectos fueron propuestos Rasmussen (1956) citado por Prem S.
(1975, p. 63) utilizado en el trabajo de Fernández (1994) y que en esta
investigación también se utilizará.
Para calcular los índices propuestos por Rasmussen es necesario contar con la matriz inversa de Leontief (I-A)-1, si denotamos cada elemento de esta matriz como Kij , que son los coeficientes de requisitos
directos e indirectos y la suma de los elementos de cada columna j
representa el producto bruto agregado que se genera de un incremento
de una unidad en la demanda final de la industria j.
La medición de encadenamientos hacia atrás está dada por:
n
Kj = ∑ Kij (j =1,2,..,n)
(48)
i=1
121
Para establecer una comparabilidad, es importante observar la magnitud relativa de Kj y por lo tanto debe estar normalizado de la siguiente
manera:
U bj =
(1 / n)kj
n
(1 / n )∑ Kj
(49)
(i, j =1,2,..,n)
2
j =1
El numerador es el valor promedio de los elementos de la columna j,
mientras que el denominador es el valor promedio de todos los elementos de la inversa. Los valores Uj b > 1, nos indica que hay un alto
grado de eslabonamiento hacia atrás, en el sentido de generar un reacción sobre el promedio de los sectores.
La medición de encadenamientos hacia adelante está dada por la
suma de los elementos de las filas:
n
Kj = ∑ Kij (j =1,2,..,n)
(50)
i=1
Para establecer una comparabilidad, es importante observar la magnitud relativa de Ki y por lo tanto debe estar normalizado de la siguiente
manera:
U fi =
(1 / n)ki
n
(1 / n )∑ Ki
(51)
(i, j =1,2,..,n)
2
i =1
El numerador es el valor promedio de los elementos de la fila i, mientras que el denominador es el valor promedio de todos los elementos
de la inversa. Los valores U if > 1, nos muestra las dependencias de los
sectores que están por encima del promedio, de la producción
de los otros sectores.
Los índices U jb y U if, usados como medidas de encadenamientos hacia
delante y hacia atrás, han sido denominados índices de poder disper-
122
sión e índices de sensibilidad de dispersión, respectivamente, por
Thurburn (1971) y Rasmussen (1956) citado por Haji (1987, p. 11911192).
Fernández (1994, p. 40) muestra que U bj > 1 indica que la industria
depende con mayor fuerza del resto del sistema que del promedio del
sector y un U if > 1 significa que la industria i podría incrementar su
producción más que el resto de los sectores por unidad de incremento
en la demanda final de cada sector. El sector clave es aquel en que
simultáneamente Ujb y Uif son mayores que uno.
Fernández (1994, p. 41) señala:
Las medidas de eslabonamiento no deberían ser confundidas con los multiplicadores sectoriales (ingreso y empleo).
Los multiplicadores sectoriales están diseñados para medir
el impacto, sobre el ingreso o el empleo, de un incremento
en la demanda final. Los índices de eslabonamientos están
diseñados para medir el impacto de un incremento en la demanda final sobre la producción bruta. Un alto valor de U bj
y Uif no implica un valor correspondientemente alto para los
multiplicadores de ingreso o empleo, un punto que es pasado por alto por algunos escritores quienes parecieran asumir
que un alto grado de eslabonamiento significa un alto valor
añadido en el contenido doméstico.
Dirven (2002) y Fernández (1994) coinciden que una vez identificados los sectores claves, nos da una señal dentro del circuito económico de generación de bienes y servicios de en que dirección debemos
hacer las inversiones tanto en capital como en trabajo para el desarrollo y dinamización como estrategia para el crecimiento industrial; por
otro lado, Pavía y Cabrer (2003) que analizan un conjunto de índices a
partir de la matriz inversa de Leontief que permiten estudiar las características e intensidad de los flujos migratorios interregionales e
intraregionales, cuya metodología propuesta se aplica al caso concreto
de las comunidades autónomas españolas.
123
V. BASES METODOLÓGICAS
El presente apartado tiene como objetivo proporcionar el marco
metodológico para desarrollar y analizar el MIP como un instrumento
de análisis económico; bajo esta perspectiva, se hace mención a un
conjunto de módulos con sus respectivos pasos de trabajo, para comprender de manera sistemática como opera el modelo dentro de esta
investigación. El primer módulo, enmarca el método de agregación de
productos, actividades y variables del Cuadro de Oferta y Utilización
(COU) utilizado, por consiguiente, permite trabajar la matriz InsumoProducto de una forma más reducida y facilita el manejo de los datos,
aunque cualquier desagregación será posible si se cuenta con las diferentes tablas de correspondencia productos-actividades y de las tablas
de agregación.
El segundo módulo, expone la operatividad del método de corrección
de los productos secundarios y el cálculo de la inversa, como base
para deducir el análisis de Insumo-Producto; el tercer módulo, explica
la manera como se determinan los requerimientos primarios de personal ocupado y formación bruta de capital, ante variaciones exógenas
en la demanda final. Por otro lado, el cuarto módulo, incorpora la metodología utilizada en la construcción de los índices de encadenamiento
intersectorial y en la determinación de los sectores claves de la economía.
Finalmente, en el módulo cinco, se mostrará las ecuaciones fundamentales para el cálculo del Producto Interno Bruto, por la vía del ingreso,
el gasto y la producción; necesarios para observar el movimiento y los
cambios en agregados macroeconómicos, y por otra parte visualizar la
generación de ingreso dentro del Modelo Insumo-Producto dentro de
la economía.
124
V.1
MÓDULO 1: Método de agregación de productos, actividades
y variables del COU
El Modelo de Insumo-Producto en esta investigación, es obtenido a
partir del Cuadro de Oferta y Utilización (COU) de la economía venezolana, siendo este un resultado de la Gerencia de Estadísticas Económicas del BCV en la culminación del Programa de Actualización de
las Estimaciones Macroeconómicas (Pracem) y la implementación del
nuevo Año Base, 1997.
El COU muestra la producción y circulación de los bienes y servicios
de la economía y la generación del ingreso. En este sentido, el COU es
equilibrado, es decir, la Oferta Total y la Demanda Total valoradas a
precios de comprador son iguales (OT(Pc) = DT(Pc)); por lo tanto, en la
apertura de estos agregados totales se encuentran las variables necesarias e indispensables para la construcción de los cuadros simétricos de
Insumo-Producto.
La OT(Pc) y DT(Pc)) se puede desagregar de la siguiente manera:
OT (Pc) = (PM Pb +PNM Pb +PUFP (Pb) ) +[(MD =MT +MCaM
(1)
+MCaD)] +M(Cif) +AjM(Cif -Fob)) + IMPN
DT(Pc) = CI (Pc) +[(CF = CFH + CPNL+ CAPI + CAPC)] +
(2)
[(FBK = FBCF + VE +OVA)] + X (Fob)
Notaciones:
OT(Pc)=
Oferta Total (Precios de Comprador)
Pc =
Precios de Comprador
PM Pb =
Producción de Mercado (Precios básicos)
PNM Pb =
Producción de No Mercado (Precios básicos)
PUFP Pb = Producción para Uso Final Propio (Precios básicos)
Pb =
Precios Básicos
MD =
Márgenes de Distribución
125
MT =
Márgenes de Transporte.
MCaM =
Márgenes de Comercio al por Mayor.
MCaD =
Márgenes de Comercio al Detal
M(Cif) =
Importaciones (CIF).
AjM(Cif -Fob) =Ajuste CIF - FOB sobre Importaciones.
DT(Pc) =
Demanda Total (Precios de Comprador)
CI =
Consumo Intermedio
CF =
Consumo Final.
CFH =
Consumo Final de los Hogares
CPNL =
Consumo Final Privado no Lucrativo
CAPI =
Consumo Final de Administración Pública Individual.
CAPC=
Consumo Final de Administración Pública Colectiva.
FBK =
Formación Bruta de Capital.
FBCF =
Formación Bruta de Capital Fijo
VE =
Variación de Existencias.
OVA =
Objetos Valiosos
X (Fob) =
Exportaciones (FOB)
IMPN =
Impuesto a los Productos Netos
Retomando la visión del Cuadro de Oferta y Utilización de Venezuela,
éste se dispone en una matriz rectangular, desagregado de acuerdo a la
Clasificación de Productos de Venezuela (CPV) en 300 productos (filas) por 127 actividades32 (columnas), tanto para la producción como
el consumo intermedio, también se tiene el valor agregado por actividades, y otras variables como la formación bruta de capital y el personal ocupado formal asociado a cada actividad económica; además, se
cuenta con la apertura de las variables de demanda final por productos.
32
Para el Modelo Insumo-Producto serán llamadas industrias.
126
Cabe mencionar, que cada una de las actividades del COU es una agregación de establecimientos homogéneos; en la cual éstos son empresas o partes de ellas situados en un lugar único, que realiza una sola
actividad de producción, en donde la mayor parte de su valor agregado
proviene de la actividad principal.
La información utilizada del Cuadro de Oferta y Utilización pertenece
al año base 1997, observándose que los valores corrientes son iguales
a precios constantes y por lo tanto, los precios son iguales a uno (1);
sin embargo, es preciso aclarar que en este trabajo no se incorpora el
análisis en la variabilidad de los precios, debido a que las variables
utilizadas se disponen sólo en términos constantes.
En este mismo orden de ideas, es necesario contar con un conjunto de
tablas de correspondencias adecuadas a la (CPV) y la Clasificación
Internacional de Industrias Uniforme (CIIU), que facilite las conversiones, agregaciones y simplificaciones del COU. Bajo esta perspectiva,
se transformó el COU rectangular de 300 productos por 127 actividades a un COU cuadrado, de 127 productos por 127 actividades y para
ello se usó la tabla 1 especificada en el apéndice. Esta tabla muestra
una concatenación de los códigos de los 300 productos y su correspondencia con las 127 actividades según la CPV y la CIIU, por lo
tanto, es la primera agregación para la construcción de matrices cuadradas del Modelo Insumo-Producto.
Luego de tener la correspondencia de los 300 productos y las 127
actividades, se le incorpora la compatibilización de los clasificadores
de la CIIU a dos (2) Dígitos (Tabla 2 Apéndice), con la finalidad, de
obtener matrices cuadradas del COU a un nivel agregación de 59 productos por 59 actividades, asociados a los 300 productos y las 127
actividades. Por último, se trabaja con una agregación mayor asociada
a los códigos de Catálogo o a un (1) Dígito de la CIIU (tabla 3 Apéndice) que corresponde de trece (13) productos por trece (13) actividades; esta agregación usada para desarrollar este trabajo puede ser
observada en la Tabla 4 y 4.1 de este capítulo y en el apéndice.
127
Tabla 4
Agregación final de las matrices Insumo-Producto cuadradas 13 x
13 a nivel de un de la CIIU
CODIGO
CIIU 1 DIG
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
AGREGACIÓN INSUMO PRODUCTO 13 x 13
CÓDIGO
CIIU
DESCRIPCIÓN CIIU 1 DIG (13 x 13)
1 DIG
Agricultura, ganadería, caza y silvicultura
A
Agricultura, ganadería, caza y silvicultura
Pesca
B
Pesca
Explotación de Minas y Canteras
C
Explotación de Minas y Canteras
Industrias Manufactureras
D
Industrias Manufactureras
Suministro de Electricidad, gas y agua
E
Suministro de Electricidad, gas y agua
Construcción
F
Construcción
Comercio
G
Comercio
Hoteles y restaurantes
H
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
I
Transporte, Almacenamiento y comunicaciones
Intermediación financiera
J
Intermediacion financiera
Actividades inmobiliarias, empresariales y de alquiler
K
Actividades inmobiliarias, empresariales y de alquiler
Administración Pública y Defensa
L
Administración Pública y Defensa / Enseñanza / Salud
Enseñanza
L
Administración Pública y Defensa / Enseñanza / Salud
Servicios Sociales y de Salud
L
Administración Pública y Defensa / Enseñanza / Salud
Otras actividades
O
Otras actividades
Hogares Privados con Servicios doméstico
O
Otras actividades
Organizaciones y órganos extraterritoriales
O
Otras actividades
DESCRIPCIÓN
CIIU 1 DIG
Tabla 4.1
Agregación final de las matrices Insumo-Producto cuadradas 13
x 13 a nivel de un de la CIIU
NUM
1
2
3
4
5
6
7
8
9
10
11
12
13
CODIGO
CIIU 1 DIG
A
B
C
D
E
F
G
H
I
J
K
L
O
DESCRIPCIÓN
CIIU 1 DIG (13 x 13)
Agricultura, ganadería, caza y silvicultura
Pesca
Explotación de Minas y Canteras
Industrias Manufactureras
Suministro de Electricidad, gas y agua
Construcción
Comercio
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
Intermediación financiera
Actividades inmobiliarias, empresariales y de alquiler
Administración Pública y Defensa / Enseñanza / Salud
Otras actividades
En atención a lo planteado, si se hace uso de las bases de datos primarias y de las tablas 1, 2 y 3 del Apéndice, es posible realizar agregaciones
a matrices simétricas del COU a 127 x 127, 59 x 59, 13 x 13 (productos
por actividades) y cualquier otra agregación que se considere necesaria, dentro de los límites ya mencionados. Ahora bien, en esta investigación se trabajó con matrices de 13 productos por 13 actividades, de
128
este modo permite hacer más fácil el análisis de las relaciones InsumoProducto, la aplicación de la metodología para corregir los productos
secundarios y los cálculos matriciales del MIP, pero una vez analizado
su aplicabilidad y factibilidad puede ser trabajado a un nivel de
desagregación de productos y actividades mayor.
Una vez determinados los niveles de agregación, se debe evaluar el
manejo de cada una de las variables del Cuadro de Oferta y Utilización y su inclusión dentro del Modelo Insumo-Producto, para ello, se
revisó el Manual de Compilación de los Cuadros Insumo-Producto de
las Naciones Unidas (2000). En este sentido, se dedujo uno de los
análisis básicos de la valoración de la producción y el consumo intermedio dentro del MIP, en este contexto las Naciones Unidas (2000) al
igual que el Instituto Nacional de Estadística e Informática de Perú
(2001), hacen la recomendación de trabajar las variables de OT (1) y
DT (2) a precios básicos. Por consiguientes, los márgenes de distribución e impuestos netos sobre los productos que hacen que la OT este a
precios de comprador33 se deducen de esta y se incorporan a la DT
negativamente para no romper el Balance entre Oferta Total y Demanda Total (OT = DT) del COU.
Despejamos de (1) los impuestos netos sobre los productos y los márgenes de distribución (MD y IMPN) pasándose con signo contrario a
(2), y se obtiene (3) y (4). En esta operación, se obtiene la OT y DT
valoradas a precios básicos.
OT(Pb) = (PM Pb+PNM Pb+PUFP Pb)) + M(Cif) +AjM(Cif -Fob))
(3)
DT(Pb) = CI (Pc) +[(CF = CFH + CPNL+ CAPI + CAPC)] +
[(FBK = FBCF + VE +OVA)] + X (Fob) - [(MD =MT
+MCaM +MCaD)] - IMPN
(4)
33
(Productos Nacionales) Precio de comprador = Precios Básicos +márgenes de comercio +
márgenes de transporte + impuestos netos sobre los productos (Productos Importados)
Precio de comprador = Precios CIF + derechos de importaciones + márgenes de distribución
y comercio + impuestos netos sobre los productos.
129
También se debe señalar que se trabajó con una demanda final neta, es
decir, el vector de las Importaciones M(Cif) y el ajuste cif -fob sobre las
importaciones AjM(Cif -Fob)), ubicado dentro de la OT(Pc) (1) se resto de
ésta y se pasó a la DT(Pc) (2); Por consiguiente, se va a encontrar, un
vector de exportaciones netas (X (Fob) - M(Cif) - AjM(Cif -Fob)) que mantiene
el Balance (OT = DT) (5 y 6).
OT(Pb) =(PM Pb+PNM Pb+PUFP Pb))
(5)
DT(Pb) = CI (Pc) +[(CF = CFH + CPNL+ CAPI + CAPC)] +
[(FBK = FBCF + VE + OVA)] + (X (Fob) - M (Cif) AjM(Cif -Fob)) - [(MD =MT +MCaM +MCaD)] - IMPN
(6)
Finalmente, también se cuenta con un vector de producción total, que
es una agregación de PM (bienes y servicios que se venden o disponen
en el mercado) +PUFP (son productos que el productor utiliza y conserva para su propio consumo final o formación bruta de capital fijo) +
PNM (es la producción suministrada a otras unidades gratuitamente o
a precios económicamente no significativos). Cabe considerar por otra
parte, que el consumo intermedio se trabajó de manera total, por imposibilidad de desagregarlo entre consumo nacional y consumo importado, a pesar de, que se pueden construir un conjunto de coeficientes de
destino asociados a cada actividad que facilitaría mejorar algunos análisis a posteriori.
V.2 MÓDULO 2: Método de corrección de los productos secundarios y cálculo
de la inversa
Una vez determinados los procesos de agregación y de valoración de
la OT y DT, se procedió al análisis y corrección de los productos secundarios dentro del MIP, ya que uno de los supuestos básicos del
modelo, es la homogeneidad en la función de producción. En este sentido, se trabajó con un método matemático denominado “supuesto de
tecnología de la industria” descrito y analizado en los capítulos III y
IV, el cual supone, que para obtener un producto en una actividad,
todos los insumos se utilizan o deben utilizarse en la misma propor-
130
ción. La simplificación obtenida en este supuesto, permite entregar
siempre coeficientes técnicos positivos y se puede aplicar a tablas de
producción rectangular, donde difiere el número de productos al número de actividades.
Para el desarrollo del módulo y la colocación en práctica de la hipótesis de tecnología de la industria, se hará mención a un conjunto de
pasos, que muestra como opera esta hipótesis dentro del grupo de variables asociadas al COU y al MIP de una forma esquemática. Por
consiguiente, se puede enumerar de la siguiente manera:
Paso 1. Definición de las matrices U (Consumo Intermedio) y V (Producción) dentro del COU, ya agregadas a 13 productos x 13 actividades.
Producción de las Actividades
TOTAL
2
n
gn
OTm MAm IVAm ISm
qm
Oferta
Vmxn
Mm
Umxn
Xm
=B
ala
nce
=
Fm
DTm
Demanda
Prod.
p1
p2
1
pm
CI
p1
p2
Donde:
m=n
Cm
pm
Otras
FBKF
VE
PO
VABn
Ma tr i z I n s u m o - P r o d u c to
VA
REO
EE
IM
ODn
Corriente / Constante / Deflactores
Total
131
Pub
Pri
Fin
Soc
Nsoc
Paso 2. Se calcula la matriz de coeficientes técnicos producto por actividades y la matriz de participaciones de los productos en el mercado
por actividades, definidos en el modelo teórico del capítulo IV, para
así, obtener la matriz de coeficientes técnicos A producto por producto.
B = U.
gˆ -1
D = V’.
q̂-1
Matriz de coeficientes técnicos, producto por
actividades
Matriz de participación
actividades
en
el
mercado
por
U : Matriz de C. Intermedio (absorción) (m productos x n actividades)
V : Matriz de producción (oferta) (m productos x n actividades)
g : Vector columna de producción intermedia por actividad (nx1) (suma por
columna de la matriz U)
q : Vector columna de producción por producto (mx1) (suma por fila de la matriz
V)
g : Matriz diagonal con la producción intermedia por actividad ( n x n)
qˆ: Matriz diagonal con la producción por producto
Paso 3. Obtención de la matriz de coeficientes técnicos producto por
producto (A = BxD), asociado a la hipótesis de la tecnología de la
industria.
Prod.
p1
p2
Producción de las Actividades
TOTAL
1
2
productos
n
p1
gn
qm
Actividades
Donde:
m=n
Vmxn
pm
CI
p1
p2
1
2
p2
pm
Dnxm = Vnxm q-1n
n
Umxn
pm
Actividades
p1
p2
2
productos
p1
n
productos
productos
1
Bmxn = Umxn g-1n
pm
132
p1
p2
pm
p2
pm
Amxm = Bmxn Dnxm
Paso 4. Cálculo de la matriz inversa de Leontief producto por producto, que permite determinar cuál es el efecto de cambios en la demanda
final de productos sobre la producción total.
AAI,CC
D
I,CC = BB x B
Matriz de coeficientes técnicos, producto por
producto.
Después llegamos a las siguientes igualdades
#
qq == Bg
Bg ++ Yi
Yi
G
gg = Dq
Dq
q = BDq
q
BDq + Yi
Yi
-1 Yi
Yi == qq (*)
(*)
(I
(I -- BD)
BD) -1
La matriz (I-BD)-1 = (I-A)-1 se denomina la matriz inversa de Leontief o
matriz de requerimientos directos e indirectos (producto por producto)
Paso 5. Cálculo o estimación de la producción total (OT) con el uso de
la inversa de Leontief a partir de variaciones exógenas de Demanda
Final (DF). Los cambios en las variables de DF se hacen a nivel agregado y se apertura por los coeficientes de participación de los componentes de la demanda en el Año Base 1997; por otro lado, al multiplicar
la Inversa de Leontief por la DF se obtiene la OT, luego el CI y VAB se
calculan a través de los coeficientes técnicos y los coeficientes de costos, respectivamente; en sentido el CI total también llamado Demanda
Intermedia (DI) por productos lo sumamos a la DF obteniéndose la
Demanda Total (DT) que es igual a la OT.
Productos
sumatoria
VABm
VA
REO
EE
IM
Otras
FBKF
VE
PO
ODm
Xm
-Mm
=
OT
CGCm
Umxm
DIm
pm
Impacto en DF
m
CGIm
2
A plic a c ión de c oefic ientes
CI
p1
p2
1
CHm
TOTAL
Fm
DFm DTm
DT
OT
OT = (I – A)-1 * DF
(I – A)-1
OT
133
DF
V.3
MÓDULO 3: Determinación de los requerimientos primarios
de personal ocupado y formación bruta de capital
Este módulo, muestra la determinación del empleo de los factores primarios, del Personal Ocupado (número de trabajadores) y Formación
Bruta de Capital (corresponde a los flujos de adquisiciones menos disposiciones de activos no financieros y activos fijos tangibles) requeridos por las industrias dentro del proceso productivo.
Bajo esta perspectiva, la determinación del Personal Ocupado (PO) y
Formación Bruta de Capital (FBK) se puede exponer esquemáticamente en los siguientes pasos:
Paso 1. Definición de los vectores F1 (PO) y Fß (FBK) dentro del Cuadro de Oferta y Utilización (COU), agregado a las trece (13) actividades y se determina los coeficientes primarios de cada una de estas
variables, que es el valor de la variable sobre la producción total de la
actividad a la cual está asociada.
(a)
FF 1=1= FF 1212 + FF 1212 + FF 1313 + …….. + FF 1n1n
Personal Ocupado (PO)
(b)
F2 = F21 + F22 + F23 +…….. + F2n
Formación Bruta de Capital
(FBK)
(c)
ffijij = FFijij / XXjj
Los fij son los coeficientes
primarios y los Fij son las FBK
o PO requeridos por dichos
sectores
i,ji,j = (1,2,3……)
(1,2,3……)
Paso 2. Se expresa los vectores de coeficientes de los requerimientos
primario f1 y f2 en forma matricial, como lo refleja teóricamente el
Modelo Insumo-Producto para la determinación del PO y la FBK (capítulo IV).
134
Expresando los coeficientes en forma matricial:
f=
((d)
f1j, es el personal ocupado
para producir una unidad de
producto en el sector j, y f2j, es
la formación bruta de capital
requerido para producir una
unidad de producto en el sector
j.
f11 f12 f13 ... f1n
f21 f22 f 23 ... f2n
F = f*X
((e)
(I-A)-1 Y = X
F = f*(I-A)-1 Y
Determina los cambios en
los
requerimientos
de
insumos primarios (PO y
FBK), ante variaciones de la
demanda final
Paso 3. Se calcula la matriz de participación de la producción de cada
actividad en el total del mercado (D) y se transpone; en este sentido, se
multiplica la matriz de coeficientes primarios [f] por la matriz D, para
obtener matriz de requerimientos primarios asociados a los productos
(F1). Por otro lado, se multiplica (F1) por la inversa de Leontief y por el
vector de demanda final (DF) con el fin de determinar los requerimientos de PO y FBK ante impactos exógenas de DF.
Expresando los coeficientes en forma matricial asociados a productos:
(f)
D = Vt. q̂-1
matriz de participación de la
producción de cada actividad
en el total del mercado
f11 f12 f13 ... f1n
f21 f22 f 23 ... f2n
(d)
f=
(e)
F1 = f1*X
(I-A)-1 Y = X
f1 = f*Dt
1*(I-A)
-1-1Y
FF1 1==f1f*(I-A)
135
Determina los cambios en
los
requerimientos
de
insumos primarios (PO y
FBK), ante variaciones de la
demanda final
V.4
MÓDULO 4: Determinación de los sectores claves de la economía
a partir del MIP
Una vez utilizado e incorporado el método matemático de la hipótesis
de la tecnología de la industria, calculado la inversa y los requerimientos primarios de PO y FBK; se incorpora el análisis de los conceptos
de eslabonamientos intersectoriales hacia atrás y hacia delante descritos el Capítulo IV para la determinación de los sectores claves de una
economía. Esto consiste en aplicar los índices propuestos Rasmussen
(1956) citado por Prem S. (1975, p. 63) y también usados en el trabajo
de Fernández (1994) que consideran tanto los efectos directos como
indirectos a partir del uso de la Inversa de Leontief para construir los
dos índices de encadenamiento intersectoriales.
El primero, es el índice de encadenamiento hacia atrás, que es un coeficiente donde el numerador es el valor promedio de los elementos de
la columna j, mientras que el denominador es el valor promedio de
todos los elementos de la inversa; en este sentido los valores U jb > 1,
nos indican que hay un alto grado de eslabonamiento hacia atrás, indicando la generación de una reacción sobre el promedio de los sectores.
El índice de encadenamiento hacia delante, es un coeficiente donde el
numerador es el valor promedio de los elementos de la fila i, mientras
que el denominador es el valor promedio de todos los elementos de la
inversa. Los valores Uif > 1, nos muestra las dependencias de los sectores que están por encima del promedio, de la producción de los otros
sectores. El sector clave es aquel o aquellos en que simultáneamente
Ujb y Uif son mayores que uno.
V.5 MÓDULO 5: Determinación del Producto Interno Bruto por la vía del
ingreso, el gasto y la producción
En el presente módulo, se muestran el conjunto de ecuaciones necesarias para el cálculo de PIB por las tres vías o enfoques (ingreso, gasto,
136
producción), esto permitirá hacer un seguimiento más claro sobre las
variables que conforman el PIB y su breve caracterización.
Es importante mencionar, que estas variables son obtenidas a partir de
cambios observados o estimados de la demanda final, dentro del Modelo
Insumo-Producto aplicado a la economía venezolana, por lo tanto, estas
pueden calcularse exógenamente al modelo (en el caso de la demanda
final) y endógenamente por medio de usos de los coeficientes de las
variables con respecto al año base (Consumo y Valor agregado).
Se elige como variable central el PIB, por ser la variable principal para
entender la producción agregada de bienes y servicios y el crecimiento
de una economía; aunado al hecho que el PIB pretende ser una medida
del valor creado por la actividad productiva de las unidades institucionales o actividades económicas llevadas a cabo por residentes (FMI,
OCDE, Naciones Unidas, 1993: párrafo 6.237).
Ahora vamos a mencionar cada unos de los enfoques por separado.
Enfoque del Ingreso:
Según el FMI, OCDE, Naciones Unidas (1993) el PIB desde el enfoque del ingreso es igual a la suma de los empleos del valor agregado
bruto dentro de la economía total.
PIBI = [(RA = SS + CS)] + OIP + OSP + EEB + IMB - CCF +
IVA + SUB + IMP + DM
REO = Remuneraciones a los Asalariados (es la remuneración total,
en dinero o en especie, a pagar por una empresa a un asalariado en
contraprestación del trabajo realizado por éste durante el período contable).
137
SS = Sueldos y Salarios (incluyen el valor de cualquier contribución
social, incluido el suministro de bienes o servicios a los asalariados
como remuneración en especie en lugar de, o además de, la remuneración en dinero).
CS = Contribuciones Sociales (son los desembolsos hechos por los
empleadores con el fin de obtener prestaciones sociales para sus asalariados; las contribuciones sociales de los empleadores pueden ser efectivas o imputadas y su finalidad es asegurar a sus asalariados el derecho a
recibir prestaciones sociales si ocurren ciertos sucesos o se dan determinadas circunstancias, que puedan afectar negativamente al ingreso
o al bienestar de sus asalariados: enfermedad, accidente, despido, jubilación, etc).
OIP = Otros Impuestos a la Producción (comprenden todos los impuestos, excepto los que gravan los productos, que recaen sobre las
empresas por el hecho de dedicarse a la actividad productiva y se pagan con independencia de la rentabilidad de la producción).
OSP = Otros Subsidios a la Producción (comprenden las subvenciones, excepción hecha de las subvenciones a los productos, que las
empresas residentes pueden recibir como consecuencia de su participación en la producción, ejemplo, subvenciones a la nómina salarial
o para reducir la contaminación).
EEN = Excedente de Explotación Neto (es una medida del excedente
derivado de los procesos de producción, después de deducir el consumo de capital fijo, basado en un concepto de intereses y de rentas de la
tierra u otras rentas de la propiedad recibidos por los activos financieros, por tierras y terrenos o por otros activos tangibles no producidos
dentro del proceso de producción de aquellas empresas constituidas
en sociedades).
138
IMN = Ingreso Mixto Neto (es la expresión del ingreso de las empresas no constituidas en sociedad (cuasisociedades) propiedad de los
miembros de los hogares, ya sea a título individual o en forma conjunta
con otros, después de deducir el consumo de capital fijo).
CCF = Consumo de Capital Fijo (es un costo de la producción, definido en términos generales como la declinación experimentada, durante
el período contable, en el valor corriente del stock de activos fijos que
posee y que utiliza un productor, como consecuencia del deterioro físico, de la obsolescencia normal o de daños accidentales normales).
IVA = Impuestos Tipo IVA (es un impuesto sobre los bienes o servicios
que las empresas recaudan por etapas, pero que en definitiva recae en
su totalidad sobre los compradores finales).
SUB = Subvenciones a los Productos (es el que se paga por unidad de
un bien o servicio. La subvención puede ser un monto específico de
dinero por unidad de cantidad de un bien o servicio o bien puede calcularse ad valorem como un porcentaje determinado del precio por
unidad).
IMP = Impuesto a los Productos (es aquél que se paga por unidad de
un determinado bien o servicio, se pueden medir en términos de unidades discretas o en términos de variables físicas continuas como el volumen, peso, potencia, distancia, tiempo, etc.; o puede calcularse ad
valorem como un porcentaje específico del precio por unidad o del
valor de los bienes o servicios transado).
DM = Derechos de Importación (comprenden los derechos de aduana,
u otras cargas sobre la importación, que recaen sobre determinados
tipos de bienes cuando entran en el territorio económico. Los derechos
se hallan especificados en el listado de aranceles aduaneros).
139
Enfoque del Gasto:
Según el FMI, OCDE, Naciones Unidas (1993) el PIB desde el enfoque del gasto, es igual a la suma de las categorías de usos finales a
precios de comprador (las importaciones se consideran negativas).
•
PIBG = CHOG + CISFLSH + [(CGOB = CGOB_I + CGOB_C)] +
FBCF + V ADOV + X - M
CHOG = Consumo de los hogares (consiste en una amplia gama de
los bienes o servicios de consumo adquiridos por los hogares individuales, sea comprándolos o bien mediante transferencias sociales en
especie recibidas de las unidades gubernamentales o de las instituciones sin fin de lucro que sirven a los hogares (ISFLSH)).
CISFLSH = Consumo de instituciones sin fines de lucro que sirven a
los hogares (son los gastos en bienes y servicios de consumo, ya se
trate de servicios colectivos o de ciertos bienes o servicios individuales, que son financiados fundamentalmente con suscripciones, contribuciones o donativos, o bien con rentas de la propiedad).
CGOB = Consumo de gobierno (son los gastos en bienes y servicios
de consumo, ya se trate de servicios colectivos o de ciertos bienes o
servicios individuales, que son financiados principalmente mediante
impuestos u otros ingresos gubernamentales).
CGOB_I = Consumo de gobierno individual (son los gastos realizados por el gobierno a nivel nacional relacionados con servicios individuales como los de salud y enseñanza).
CGOB_C = Consumo de gobierno colectivo (cuando se refieren a la
formulación y administración de la política gubernamental, a la fijación y aplicación de normas públicas, a la regulación, habilitación o
supervisión de los productores, etc.).
140
FBCF = Formación bruta de capital fijo (se mide por el valor total de
las adquisiciones, menos las disposiciones, de activos fijos efectuadas
por el productor durante el período contable, más ciertas adiciones al
valor de los activos no producidos realizadas por la actividad productiva de las unidades institucionales).
VE = Variación de existencias (es igual al valor de las existencias adquiridas por una empresa menos el valor de las existencias dispuestas
durante el período contable).
ADOV = Adquisiciones menos disposiciones de objetos valiosos (estos objetos se definen como bienes de considerable valor que no se
usan primordialmente para fines de producción o consumo, sino que se
mantienen a lo largo del tiempo como depósito de valor, ejemplo las
obras de arte).
X = Exportaciones (f.o.b)34 (Las exportaciones de bienes y servicios
consisten en ventas, trueques, regalos o donaciones, de bienes y servicios de los residentes a los no residentes).
M = Importaciones (f.o.b)35 (consisten en compras, trueques o la percepción de regalos o donaciones, de bienes y servicios por los residentes de los no residentes).
34
Las exportaciones e importaciones de bienes se valoran f.o.b. -es decir, incluidos los costos
de transporte y seguro hasta la frontera del país exportador -, aun cuando en otros contextos,
como los cuadros de Insumo-Producto, los costos de transporte y seguro pueden presentarse
por separado del precio de productor o del precio básico de un bien cuando sale de las
instalaciones de su productor.
35
Ibídem.
141
Enfoque de la Producción:
El PIB desde el enfoque de la producción es igual a la suma del valor
agregado bruto por productos (actividades homogéneas) a precios básicos, más una sola partida de impuestos menos subvenciones sobre
los productos y derechos de importación. (FMI, OCDE, Naciones
Unidas, 1993).
•
PIBP = VBP - CI + IVA + SUB + IMP + DM
PB = Valor Bruto de la Producción a precios básicos (son los bienes y
servicios obtenidos en los procesos de producción, incluidos los servicios producidos por las actividades auxiliares, por consiguiente, la producción consiste únicamente en aquellos bienes o servicios producidos dentro de un establecimiento que están disponibles para su empleo
fuera de ese mismo establecimiento. Cuando una empresa consta de
más de un establecimiento, la producción de la empresa es la suma de
las producciones de los establecimientos que la componen).
CI = Consumo Intermedio (consiste en el valor de los bienes y servicios
consumidos como insumo por un proceso de producción, excluidos los
activos fijos cuyo consumo se registra como consumo de capital fijo).
IVA = Impuestos Tipo IVA (véase enfoque del ingreso)
SUB = Subvenciones a los Productos (véase enfoque del ingreso)
IMP = Impuesto a los Productos (véase enfoque del ingreso)
DM = Derechos de Importación (véase enfoque del ingreso)
142
VI. RESULTADOS
Este capítulo tiene como objetivo proporcionar los resultados adjuntos
a esta investigación, con la finalidad de mostrar que el Modelo InsumoProducto (MIP) es un instrumento adicional de interpretación y análisis estadístico-económico. En la primera parte se expone la matriz de
coeficientes técnicos, uno de los elementos centrales para la observación de una economía con el uso de la técnica Insumo-Producto, luego
se incorpora el análisis de la matriz inversa de Leontief o matriz de
requerimientos directos e indirectos, siendo ésta la que permite determinar cuánto debe producir un sector, cuya producción es requerida
por el mismo sector o por otro, necesaria para satisfacer los cambios
exógenos de demanda final.
En este mismo orden de ideas, se incorpora un análisis del Producto
Interno Bruto sectorial (según el nuevo manual del SCN, 1993, el concepto es Valor Agregado Bruto VAB Sectorial) y PIB total (incluye
IVA, SUB, IMP y DM), para así sostener la hipótesis de la investigación, con base en que el MIP permite anticipar la dirección del cambio
en estas variables, a partir de la introducción de los datos observados
de demanda final. Estos datos, han sido obtenidos en la implementación del nuevo año base 1997 en el Pracem haciendo uso de la serie
1997-2001; y en este sentido, el resultado de lo estimado en el modelo
se contrastará o se verificará con lo observado (Pracem). Cabe destacar que en esta parte, sólo se mostrarán los datos de la serie 19982001 en variaciones, ya que los mismos no han sido publicados por el
BCV para la fecha de entrega de este trabajo.
Por otro lado, también se muestra como el MIP permite simular los
impactos de la demanda final, introduciendo las variaciones exógenas
de cada una de las variables de la demanda final, obtenidas y publicadas por el BCV en términos constantes de 1984. De esta forma, se
observa como el MIP permite anticipar la dirección del cambio en el
PIB agregado; y de igual manera, como se obtiene el Producto Interno
143
Bruto, por la vía del ingreso y de la producción; ya que por el enfoque
del gasto, las variables que los componen son las variables exógenas
de demanda final.
Retomando lo expresado en la inversa de Leontief y para cerrar este
apartado, se identificarán los sectores claves de la economía a partir
del uso del Modelo Insumo-Producto.
VI.1 La Matriz de Coeficientes Técnicos producto por producto
En el Cuadro 1 se muestran los resultados de la matriz de coeficientes
técnicos (producto por producto), obtenida en la aplicación del método matemático propuesto por las Naciones Unidas (2000) definido como
hipótesis de la tecnología de la industria, el cual, fue aplicado al Cuadro de Oferta y Utilización (COU) del año 1997 de la economía venezolana.
Con el método matemático, se corrigió los productos secundarios observados fuera de la diagonal principal de la matriz de producción del
COU, con ello se demostró que los coeficientes técnicos obtenidos
son positivos y están asociados a una matriz producto por producto.
Por lo tanto, esta matriz de coeficientes técnicos es la usada para el
cálculo de la matriz inversa de Leontief del Modelo Insumo-Producto
y la interpretación de cada coeficiente técnico aij, es la cantidad de
insumos producidos por el sector36 o la industria i, que demanda el
sector j para producir una unidad de su producto.
Por otro lado, en esta matriz se observan los coeficientes de costos
asociados al Valor Agregado Bruto y con relación a sus componentes
(Remuneración de los asalariados, Otros impuestos sobre la produc36
En estos resultados, se utiliza la definición de sector como industria (agrupación de nestablecimientos), no debe confundirse con sector institucional, ya que este que agrupa nunidades institucionales, las cuales son capaces de poseer activos, contraer pasivos, realizar
actividades económicas y transacciones con otras entidades económicas.
144
ción, Otras subvenciones a la producción, Excedente de explotación
bruto, Ingreso mixto bruto, Consumo de capital fijo); debe señalarse,
que cada uno de estos coeficientes, son las estructuras de costos de
cada industria para lograr una unidad de su producto. En este mismo
orden de ideas, también se obtienen los coeficientes de la Formación
Bruta de Capital y del Personal Ocupado (Asalariados, Cuenta propia,
Empresarios, empleadores, patronos, Trabajadores familiares no remunerados) asociados a cada proceso productivo, que sirven para determinar cuáles son los niveles de estas variables ante impactos
exógenos en la demanda final. En este sentido, se asume que no hay
sustitución ni de capital ni trabajo entre las industrias y en el caso del
Personal Ocupado, existe una oferta laboral lo suficientemente grande
como para absorber los choques positivos en la producción que demanden más fuerza laboral.
También, es conveniente mencionar, que el coeficiente del valor agregado de la industria que agrupa Otras Actividades es negativo, esto se
debe a que en el proceso de agregación, este resto (Otras Actividades)
incorporó la actividad de Servicios de Intermediación Financiera Medidos Indirectamente (SIFMI) que es una industria cuyo valor de producción se trata como consumo intermedio, con producción nula y un
valor agregado negativo en la misma cuantía. El valor de los SIFMI se
calcula como el valor de la renta de la propiedad a cobrar por los
intermediarios financieros menos los intereses que éstos han de pagar.
En este sentido, como el monto ya se ha discriminado dentro del sector
financiero y por tanto dentro de su valor agregado, al observarse la
economía total el valor agregado negativo de la industria ficticia es
compensado por el del sector financiero, dejando invariante el Producto Interno Bruto total.
Por último, en atención a lo plateado en la interpretación del coeficiente técnico, si se observa el Cuadro 1, se visualiza que el coeficiente
técnico más alto es 0,92896, que corresponde a la cantidad de insumos
producidos por la actividad de Intermediación financiera y demandado
por Otras actividades para lograr una unidad del producto de esta actividad, en este sentido, es un coeficiente bastante elevado, por lo tanto,
145
DESCRIPCION
A
B
C
D
E
F
G
H
I
J
K
L
O
B
S
B.1b
D.1
D.11
D.12
D.29
D.39
B.2b
B.3b
K.1Im
K.1Ee
B.3n
B.2n
P.51
PO.1
PO.11
PO.12
PO.13
PO.14
BA
CONSUMO INTERMEDIO
146
PRODUCCION (Precios basicos)
Agricultura, ganaderia, caza y silvicultura
0
Pesca
Explotacion de Minas y Canteras
Industrias Manufactureras
Suministro de Electricidad, gas y agua
Construccion
Comercio
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
Intermediacion financiera
Actividades inmobiliarias, empresariales y de alquiler
Administracion Publica y Defensa / Enseñanza / Salud
Otras actividades
Bienes
Servicios
VALOR AGREGADO BRUTO (Coeficientes)
Remuneración de los asalariados
Sueldos y salarios
Contribuciones sociales de los empleadores
Otros impuestos sobre la producción
Otras subvenciones a la producción (-)
Excedente de explotación, bruto
Ingreso mixto, bruto
Consumo de capital fijo no sociedades
Consumo de capital fijo sociedades
Ingreso mixto, neto
Excedente de explotación, neto
Formación bruta de capital fijo
Personal ocupado
Asalariados
Cuenta propia
Empresarios, empleadores, patronos
Trabajadores familiares no remunerados
CONCEPTO
CODPROD
P.1
CONSUMO INTERMEDIO (Coef_Tecn)
CODIGO
1,00000
AI,CC
0,11727
0, 0 000 0
0 ,0 0 0 0 3
0 , 2 52 9 1
0 , 0 06 6 3
0,00094
0,02 770
0 ,0 00 0 3
0,00324
0,00227
0,02397
0,00108
0 , 0 0 0 05
0,37684
0,05927
0,56389
0,13465
0,12855
0,00610
0,00005
(0,00000)
0,28186
0,14734
0,01621
0,04062
0,13113
0,24125
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00000
0,00210
0,00000
0,18892
0,00235
0,00000
0,00027
0,00000
0,01910
0,00366
0,00341
0,00004
0,00447
0,19337
0,03096
0,77567
0,30495
0,29970
0,00525
0,00000
(0,01608)
0,34293
0,14388
0,01253
0,04983
0,13135
0,29310
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00004
0,00000
0,11545
0,06195
0,00303
0,00696
0,00187
0,00060
0,01062
0,00189
0,02246
0,00030
0,00033
0,18045
0,04504
0,77451
0,12246
0,07946
0,04300
0,00479
(0,00000)
0,63779
0,00947
0,00057
0,03975
0,00890
0,59805
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,09079
0,00221
0,06040
0,38114
0,01762
0,00478
0,00593
0,00420
0,01788
0,00579
0,03553
0,00050
0,00346
0,55215
0,07808
0,36977
0,11019
0,08434
0,02585
0,00414
(0,00003)
0,22851
0,02696
0,00072
0,01943
0,02624
0,20908
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00007
0,00000
0,00449
0,08382
0,01205
0,03665
0,01483
0,00598
0,00498
0,01924
0,10526
0,00051
0,00209
0,10043
0,18954
0,71003
0,25023
0,13322
0,11701
0,05649
(0,00000)
0,39931
0,00401
0,00032
0,09646
0,00369
0,30285
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00038
0,00001
0,04143
0,42746
0,00141
0,00803
0,00014
0,00006
0,00259
0,00013
0,04099
0,00001
0,00004
0,47069
0,05199
0,47731
0,14304
0,10624
0,03680
0,00423
(0,00000)
0,24444
0,08561
0,00317
0,09056
0,08244
0,15388
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00281
0,00007
0,00185
0,16112
0,01921
0,01540
0,01044
0,01836
0,06197
0,01090
0,10889
0,00144
0,00576
0,18507
0,23316
0,58177
0,23145
0,19532
0,03613
0,01432
(0,00004)
0,11325
0,22278
0,00651
0,01795
0,21627
0,09530
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,05385
0,00621
0,00758
0,54949
0,02443
0,00450
0,00095
0,00221
0,01325
0,01248
0,04517
0,00031
0,00974
0,64155
0,08862
0,26983
0,15417
0,13699
0,01717
0,00615
(0,00099)
0,05584
0,05465
0,00129
0,01075
0,05337
0,04509
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00041
0,00001
0,00117
0,18279
0,01170
0,00998
0,03463
0,00994
0,06386
0,00763
0,06920
0,00130
0,00539
0,19608
0,20192
0,60200
0,13699
0,09970
0,03728
0,00226
(0,00206)
0,26352
0,20128
0,00979
0,03068
0,19150
0,23284
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00000
0,00000
0,04694
0,01455
0,03248
0,00092
0,00563
0,06909
0,07811
0,15194
0,00291
0,00561
0,06150
0,34669
0,59181
0,29870
0,20263
0,09606
0,03177
0,23348
0,02786
0,00000
0,02436
0,02786
0,20912
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
1,00000
0,00329
0,00008
0,00270
0,08599
0,00684
0,00971
0,00694
0,00641
0,01623
0,01064
0,05970
0,00085
0,01864
0,09891
0,12913
0,77196
0,10006
0,08150
0,01856
0,00585
(0,00009)
0,56549
0,10064
0,00031
0,02846
0,10033
0,53704
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
PME17
1,00000
0,00296
0,00000
0,00025
0,11353
0,01170
0,00892
0,00523
0,00539
0,01076
0,01065
0,04402
0,00113
0,00558
0,12844
0,09169
0,77987
0,70132
0,51849
0,18284
0,00090
(0,00000)
0,03494
0,04271
0,00001
0,00507
0,04270
0,02987
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
PME18
1,00000
0,00036
0,00004
0,00008
0,09518
0,02717
0,02206
0,00851
0,00924
0,02718
0,92896
0,08708
0,00434
0,02770
0,12282
1,11506
(0,23789)
0,40177
0,35312
0,04865
0,00414
(0,00086)
(0,78211)
0,13916
0,00003
0,01251
0,13913
(0,79462)
0,10477
0,11889
0,06934
0,04371
0,00548
0,00036
PME19
A
Agricultura,
ganaderia, caza y
silvicultura
PME16
B
Pesca
PME15
C
Explotacion de
Minas y Canteras
PME14
D
Industrias
Manufactureras
PME13
E
Suministro de
Electricidad, gas
y agua
PME12
F
Construccion
PME11
G
Comercio
PME10
H
Hoteles y
restaurantes
PME05
I
Transporte,
Almacenamiento
y
comunicaciones
PME02
J
Intermediacion
financiera
PME01
O
L
K
Actividades
inmobiliarias,
empresariales y
de alquiler
COEFICIENTES
Administracion
Publica y
Defensa /
Enseñanza /
Salud
37
Otras actividades
NOMENCLATURA DE PRODUTOS Y TRANSACCIONES
habría que chequear cuando aporta el SIFMI al coeficiente para tener
una visión más exacta del comportamiento del producto generado en
Otras actividades37. Por otro lado, si se observa también el extremo, se
denota que la actividad Pesca no produce nada que sea demandado
por la actividad intermediación financiera para llevar a cabo su proceso productivo.
Cuadro 1: Coeficientes técnicos
Esto da indicios, para trabajar con matrices Insumo-Producto más desagregadas.
VI.2 La Matriz de Requerimientos Directos e Indirectos (Matriz Inversa
de Leontief)
La matriz inversa de Leontief (I - A)-1 ó (I - BD)-1 es la matriz de coeficientes de requisitos totales, directos e indirectos [rij] , obtenida a
partir de la aplicación de la hipótesis de tecnología de la industria y la
obtención de los coeficientes técnicos (producto por producto); por
otra parte, esta matriz permite calcular o determinar los niveles de
producción sectorial y total en términos constantes, necesarios para
satisfacer cambios exógenos en la demanda final, es decir, si observamos
cada rij, este indica cuanto debe producir el sector i cuya producción
es requerida por el sector j para satisfacer una unidad de su demanda
final.
En la diagonal principal se ubican los requerimientos directos y los
coeficientes por encima y por debajo de la diagonal se localizan
los coeficientes de requerimientos indirectos, así los coeficientes de
requerimientos directos siempre son mayores que uno; esto indica cuanto debe producir un sector cuya producción es requerida por el mismo
para satisfacer una unidad adicional de demanda final; además, cada
uno de los elementos de la inversa de Leontief están asociados a una
actividad principal (producción homogénea).
En este mismo orden de ideas, la inversa de Leontief es la matriz que
se multiplica por el vector de demanda final, para calcular la producción total (oferta total) de la economía, por consiguiente, al usar las
estructuras de los coeficientes técnicos se calculan los nuevos requerimientos de bienes y servicios que tienen como destino el consumo
intermedio y se calcula el valor agregado bruto y sus componentes
(usando los coeficientes de costos). De esta manera, el total de consumo intermedio o la demanda de bienes intermedios se adicionan a la
demanda final que es exógena y se obtiene la demanda total que en
equilibrio contable será igual a la oferta total.
147
Por último, es importante destacar como característica importante de
la economía venezolana (Cuadro 2), la observación del coeficiente de
requerimiento directo más alto de las trece industrias, el cual está asociado a la industria manufacturera y corresponde a 1,7582, este se
interpreta como lo que debe producir esta industria y que a su vez es
requerido por ella misma para satisfacer una unidad de su demanda
final, esto da una idea aproximada de que es un sector importantísimo
para la dinamización del proceso productivo en Venezuela. Por otro
lado también destaca la presencia de un coeficiente de requerimiento
indirectos de 1,0605 que corresponde a la cantidad de producto que
debe producir la actividad Intermediación financiera requerido por Otras
actividades para satisfacer una unidad de su demanda final, este coeficiente es bastante elevado, por lo tanto, habría que dilucidar cuando
aporta el SIFMI a este coeficiente para tener una visión más exacta de
lo que debe producir la actividad intermediación financiera indirectamente, para satisfacer una unidad de demanda final de otras actividades.
148
A
B
C
D
E
F
G
H
I
J
K
L
O
CODPROD
CODIGO
149
Agricultura, ganaderia, caza y silvicultura
Pesca
Explotacion de Minas y Canteras
Industrias Manufactureras
Suministro de Electricidad, gas y agua
Construccion
Comercio
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
Intermediacion financiera
Actividades inmobiliarias, empresariales y de alquiler
Administracion Publica y Defensa / Enseñanza / Salud
Otras actividades
MATRIZ INVERSA
CONCEPTO
DESCRIPCION
1,1875
0,0012
0,0367
0,5257
0,0192
0,0065
0,0379
0,0038
0,0193
0,0117
0,0618
0,0018
0,0036
0,0357
1,0029
0,0239
0,3444
0,0099
0,0035
0,0048
0,0022
0,0295
0,0138
0,0251
0,0004
0,0066
PME02
2
0,0149
0,0003
1,1409
0,1420
0,0069
0,0098
0,0044
0,0019
0,0172
0,0059
0,0372
0,0005
0,0018
PME05
3
0,1818
0,0040
0,1213
1,7582
0,0352
0,0134
0,0185
0,0092
0,0408
0,0230
0,0887
0,0014
0,0087
PME10
4
0,0237
0,0006
0,0226
0,2185
1,0187
0,0418
0,0189
0,0087
0,0162
0,0309
0,1347
0,0009
0,0060
PME11
5
0,0806
0,0018
0,1008
0,7736
0,0176
1,0150
0,0089
0,0045
0,0223
0,0120
0,0852
0,0007
0,0048
PME12
6
0,0439
0,0011
0,0297
0,3754
0,0302
0,0226
1,0186
0,0226
0,0808
0,0293
0,1512
0,0021
0,0112
PME13
7
0,1680
0,0086
0,0804
1,0300
0,0474
0,0155
0,0152
1,0087
0,0424
0,0404
0,1126
0,0014
0,0167
PME14
8
0,0430
0,0010
0,0301
0,3987
0,0230
0,0168
0,0428
0,0144
1,0836
0,0244
0,1105
0,0020
0,0102
PME15
9
0,0213
0,0005
0,0161
0,1931
0,0231
0,0413
0,0078
0,0096
0,0900
1,1015
0,1998
0,0037
0,0116
PME16
10
A
A g ric u ltu ra ,
g a n a d e ria , c a z a y
s ilv ic u ltu ra
PME01
1
J
I
H
G
F
E
D
C
B
Pesca
S
E x p lo ta c io n d e
M in a s y C a n te ra s
S
In d u s tria s
M a n u fa c tu re ra s
MATRIZ INVERSA DE LEONTIEF
S
S u m in is tro d e
E le c tric id a d , g a s
y agua
-1
S
C o n s tru c c io n
(I-A)
S
C o m e rc io
B
H o te le s y
re s ta u ra n te s
B
T ra n s p o rte ,
A lm a c e n a m ie n to
y
c o m u n ic a c io n e s
B
In te rm e d ia c io n
fin a n c ie ra
B
S
L
S
K
0,0252
0,0006
0,0179
0,2001
0,0133
0,0144
0,0110
0,0088
0,0273
0,0369
1,0860
0,0013
0,0221
PME17
11
0,0284
0,0006
0,0174
0,2360
0,0180
0,0129
0,0091
0,0075
0,0203
0,0230
0,0669
1,0015
0,0083
PME18
12
A c tiv id a d e s
in m o b ilia ria s ,
e m p re s a ria le s y
d e a lq u ile r
A d m in is tra c io n
P u b lic a y
D e fe n s a /
Enseñanza /
S a lu d
B
O
S
0,0466
0,0011
0,0338
0,4237
0,0570
0,0671
0,0213
0,0215
0,1249
1,0605
0,3084
0,0084
1,0433
PME19
13
O tra s a c tiv id a d e s
RECURSOS
Cuadro 2: Inversa de Leontief
VI.3 El producto interno bruto
Una vez determinada la matriz de coeficientes técnicos y la matriz de
requerimientos directos e indirectos, se incorporan dos modalidades
para observar si una vez conocidos los cambios en la demanda final, se
puede anticipar la dirección del cambio en el PIB por industria o Valor
Agregado Bruto sectorial y en el PIB total, para lo cual se hace uso de
los resultados de los niveles y apertura de la demanda final desde el
año 1997 al 2001 obtenida en el Programa de Actualización de las
Estimaciones Macroeconómicas38. Bajo esta perspectiva, se asume que
no existen choques tecnológicos persistentes que cambien los coeficientes técnicos y además, los precios de los factores y productos no
varían.
Al introducir la apertura de las variables de demanda final en términos
constantes (año base 1997), proporciona como resultado, que es posible anticipar la dirección del cambio en el PIB a partir de la estimación
que hace el MIP con respecto al PIB observado (obtenido en el Pracem).
En este sentido, se observa que en cada año la anticipación es completa, es decir, uno a uno, por lo tanto, hay que enfatizar que se introdujo
los niveles (a precios constantes) de cada uno de los componentes de
la demanda final, como variables exógenas. En atención a lo planteado, se debe señalar, que así como se introdujo los niveles de los topes
de las variables de demanda final y su apertura, también se desagregó
cada una de ellas usando los coeficientes del año base 1997 del MIP,
mostrando los mismos resultados para el PIB agregado en ambos casos (véase gráfico 1), es decir, la dirección de cambio en el PIB estimado mostró la misma dirección del cambio del observado (Pracem).
38
Este ejercicio es a título ilustrativo, ya que no se van a mostrar los niveles observados de
demanda final, debido a, que los mismos no han sido publicados oficialmente para la fecha
de presentación de este trabajo y por otro lado, son preliminares y sujetos a revisión.
150
Es conveniente anotar, que introduciendo los niveles exactos de demanda final observados, es posible anticipar el PIB agregado a través
del MIP; sin embargo, no necesariamente las partes del agregado va a
asumir este mismo comportamiento, es decir, el Valor Agregado Bruto
(VAB) sectorial no necesariamente se mueve en la misma dirección al
observado o lo obtenido en el Pracem, debido a que no se consideran
los cambios tecnológicos que modifiquen los coeficientes técnicos y
por otro lado, la estructura de costos permanece inalterada.
Visto de esta forma, es necesario e importante que una vez publicadas
las cifras oficiales se actualicen de nuevo los resultados y se puedan
construir MIP para cada año, es decir, para la serie 1998-2001 (Pracem), con
la finalidad de hacer una contrastación y observación más exhaustiva.
Gráfico 1. Variaciones % del PIB (MIP vs. Pracem)
3,7%
0,3%
3,4%
0,3%
-6,0%
98/97
3,7%
-6,0%
99/98
PIB OBSERVADO
00/99
PIB ESTIMADO
151
01/00
3,4%
El Gráfico 1 destaca, que el PIB total obtenido en el Modelo InsumoProducto logra anticipar la dirección del cambio con respecto al PIB
observado, pero pueden existir divergencias en el comportamiento del
VAB sectorial estimado, con relación al VAB sectorial obtenido en el
Pracem (observado).
Contrastándose las variaciones de la producción sectorial estimada y
la observada, se detecta que para los años 98/97, que 7/13 (siete de las
trece) industrias anticiparon la dirección del cambio en su VAB (estimado) con respecto al VAB observado de cada industria; en los años
99/98, 12/13 sectores o industrias anticiparon la dirección del cambio;
en 00/99, 12/13 sectores y con relación a 01/00 sólo 5/13 anticiparon
la dirección del cambio en el VAB sectorial con relación al obtenido en
el Pracem (véase cuadro 3).
Cuadro 3. Sectores que anticipan la dirección del cambio
NUM
1
2
3
4
5
6
7
8
9
10
11
12
13
N_ACT
Agricultura, ganadería, caza y silvicultura
Pesca
Explotación de Minas y Canteras
Industrias Manufactureras
Suministro de Electricidad, gas y agua
Construcción
Comercio
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
Intermediación financiera
Actividades inmobiliarias, empresariales y de alquiler
Administración Pública y Defensa / Enseñanza / Salud
Otras actividades
98/97
2
3
4
5
6
7
8
9
10
11
13
99/98
2
3
4
5
6
7
8
9
10
11
13
00/99
1
2
3
5
6
7
8
9
10
11
12
13
01/00
1
3
5
7
9
11
12
-
Al no poderse mostrar las variaciones de cada uno de los VAB de los
trece (13) sectores, debido a que los resultados todavía no han sido
publicados39, se muestra la participación del VAB de cada uno de los
sectores o industrias que anticiparon la dirección del cambio con respecto al PIB total, tanto para los estimados como para los observados
(véase gráfico 2).
39
Ibídem.
152
Gráfico 2. Participación de VAB de los sectores que
anticipan el cambio en el PIB total, tanto para el estimado
como el observado
Participación del PIB de cada una de las actividades en la PIB total
(Estimado vs Observado)
95,63
95,12
95,55
95,20
100,00
P a r ti c i p a c i o n e s %
90,00
78,49
78,89
80,00
54,83
70,00
54,58
60,00
50,00
40,00
30,00
20,00
10,00
97-98
98-99
99-00
00-01
Años
EST
OBS
Este gráfico muestra las participaciones del VAB de cada uno de los
sectores con respecto al PIB total, tanto para el estimado a partir del
Modelo Insumo-Producto como para el obtenido del Pracem (observado), en el mismo, se observa que para el período 97-98 los sectores
que anticiparon la dirección del cambio tenían una participación en
promedio del 78,49% con relación a la producción sectorial y estos
mismos sectores pesan en el observado un 78,89%. Para el período
98-99 los sectores que anticiparon la dirección del cambio tenían una
participación en promedio del 95,63% y en el observado un 95,12%,
durante 99-00 en el estimado pesaban el 95,55% y en el observado
95,20% y para el período 00-01, los sectores que anticiparon la dirección del cambio con relación al observado tienen una participación del
54,83% en el MIP y un 54,58% en el obtenido en el Pracem.
De esta manera, se observa que los cambios de los sectores o actividades que anticiparon la dirección con respecto al observado, son lo suficientemente grandes para anticipar o compensar a los que no se movieron en la dirección observada, por otro lado, se observa que los
153
sectores que se movieron en el mismo sentido del observado pesan
más de 50% en la Producción Interno Bruto total. De allí pues, que
esto aplica para la apertura de 13 x 13, pero se tendría que examinar en
matrices Insumo-Producto más desagregadas, ya que dentro de cada
industria pueden existir actividades que no necesariamente anticipan
la dirección del cambio en el VAB sectorial.
VI.4 Simulación de impactos observados en la demanda final
En esta parte, se observa también como el modelo anticipa la dirección
del cambio en el Producto Interno Bruto, haciendo uso de las variaciones interanuales de cada uno de los componentes de la demanda final
(exógenos) en términos constantes (Año Base 1984) y asumiendo que
los componentes de la demanda final del MIP del año 1997 van a adoptar
el mismo comportamiento de la serie de la demanda final base 1984, y
así se puede exponer como estos cambios repercuten en el PIB en las
grandes variables del Modelo Insumo-Producto.
Al igual que el estudio anterior, se asume que no existen choques tecnológicos persistentes que cambien los coeficientes técnicos InsumoProducto y por otro lado, los precios de los factores y productos no
varían.
Cuadro 4. Oferta y Demanda Global
DIVULGADO =PCAB
OFERTA Y DEMANDA GLOBAL
(A precios constantes 1984 = 100)
AÑOS
2003
2002
2001
2000
1999
1998
1997
VAR %
2003
2002
2001
2000
1999
1998
1997
Fuente: BCV
OFERTA TOTAL
PIB
M
TOTAL O
495.881
82.142
578.023
547.175
102.208
649.383
600.488
139.398
739.886
584.195
125.564
709.759
565.888
108.839
674.727
602.558
127.425
729.983
601.534
116.476
718.010
CG
60.194
61.006
62.585
58.816
55.999
54.357
53.594
CP
294.955
308.424
329.427
314.668
303.375
316.898
317.245
DEMANDA TOTAL
FBK
VE
TOTAL DAI
42.144
(7.900)
389.393
68.982
(3.998)
434.414
88.490
26.253
506.755
77.890
23.052
474.426
77.054
15.294
451.722
92.220
16.562
480.037
94.614
12.618
478.071
OFERTA TOTAL
PIB
M
TOTAL O
(9,37)
(19,63)
(10,99)
(8,88)
(26,68)
(12,23)
2,79
11,02
4,24
3,24
15,37
5,19
(6,09)
(14,59)
(7,57)
0,17
9,40
1,67
-
CG
(1,33)
(2,52)
6,41
5,03
3,02
1,42
-
CP
(4,37)
(6,38)
4,69
3,72
(4,27)
(0,11)
-
DEMANDA TOTAL
FBK
VE
TOTAL DAI
(38,91)
97,60
(10,36)
(22,05)
(115,23)
(14,28)
13,61
13,89
6,81
1,08
50,73
5,03
(16,45)
(7,66)
(5,90)
(2,53)
31,26
0,41
-
154
X
188.630
214.969
233.131
235.333
223.005
249.946
239.939
TOTAL DT
578.023
649.383
739.886
709.759
674.727
729.983
718.010
X
TOTAL DT
(12,25)
(10,99)
(7,79)
(12,23)
(0,94)
4,24
5,53
5,19
(10,78)
(7,57)
4,17
1,67
-
Las variaciones interanuales de los componentes de la demanda final
del Cuadro 4, se introdujeron en cada uno de los elementos de la demanda final del MIP para el año 1997 y así, sucesivamente, se hizo
para construir una serie exógena de demanda final en el Modelo InsumoProducto para cada año hasta el 2003.
Para evaluar los resultados, en primer lugar observamos que las variaciones interanuales del PIB estimado en el MIP con respecto al obtenido (observado) según lo publicado en la página Web del BCV (base
1984) en la parte Agregados Macroeconómicos, específicamente en
los cuadros de la Oferta y Demanda Global. En este sentido, el gráfico
3 ilustra que si es posible ante estos impactos exógenos de demanda
final, anticipar la dirección del cambio en el Producto Interno Bruto.
Es importante mencionar, que las variaciones introducidas fueron a
nivel agregado de las variables de demanda final y se apertura con el
uso de los coeficientes de participación de cada uno de los elementos
de las variables de demanda final en el MIP del año 1997; y por otro
lado, se asume que el tope de la variable de demanda final tiene un
comportamiento similar al observado a precios constantes del año 1984.
Este ejercicio permite ilustrar que conociendo las estimaciones de la
demanda final es posible anticipar la dirección y el comportamiento del
PIB y sus componentes usando las técnicas de programación lineal
del Modelo Insumo-Producto (véase gráfico 3).
El gráfico 3, muestra como el MIP logra anticipar la dirección del cambio en el PIB agregado menos en el 98/97; estas diferencias entre el
PIB estimado y el observado radica en que no se dispone de la apertura de cada una de las variables de la demanda final y en variaciones
muy pequeñas se marca ya la obsolescencia de año base 1984 como
indicador de la evolución de los precios, por otra parte, se está contrastando dos metodologías de medición estadística (Pcab 1984=100 y
Pracem 1997=100), y en este sentido la última se incorpora con la
adopción de nuevo SCN de 1993.
155
Gráfico 3. Variaciones del Producto Interno Bruto (MIP vs.
PCAB 1984=100)
4,0%
3,2%
2,6%
2,8%
0,2%
-0,7%
-6,1% -5,9%
-8,9%
98/97
99/98
00/99
01/00
PIB OBSERVADO
-9,5%
02/01
-9,4%
-10,8%
03/02
PIB ESTIMADO
Los componentes de la demanda final en este ejercicio se abren por los
coeficientes de la base (1997=100) y de igual manera, no se considera
cambios en los coeficientes técnicos y en los precios tanto de los factores como de los productos.
Es importante mencionar, que el Consumo Privado dentro del MIP
1997 se dispone en Consumo de los Hogares y Consumo de las Instituciones sin Fines de lucro que sirven a los hogares, y en la Base 1984
se dispone agregado; por consiguiente, para poder incorporar la variación observada de esta variable (base 1984) se abrió usando la participación de cada una de las variables que forman el Consumo Privado
en el año 1997. De la misma forma, ocurre con la formación bruta
de capital (FBK), es decir, en la Base 1984 se dispone de esta variable
más la variación de existencias, en cambio en el año 1997 se dispone
de estas mismas variables, más la adquisición de objetos valiosos,
que también forman parte de la Formación Bruta de Capital; por lo
tanto esta variable, se abrió usando la participación de adquisición de
objetos valiosos sobre la FBK del año 1997.
156
VI.5 El Producto Interno Bruto (Vía del Gasto, Producción e Ingreso)
En el Cuadro 4, se expone todo el circuito de la producción de bienes
y servicios, generación del ingreso, cuyos resultados provienen de la
introducción de las variaciones interanuales detectadas de cada uno de
los componentes de la demanda final (Base 1984) determinados anteriormente, se calcula los nuevos niveles del PIB por los tres enfoques
a partir de este impacto.
Es importante mencionar, que los componentes del PIB por la vía del
gasto son iguales a las variables de demanda final (exógenas) y a través del uso del Modelo Insumo-Producto se calcula el PIB por el enfoque del Ingreso y por la vía de la Producción. Bajo esta perspectiva, se
utiliza la inversa de Leontief para la determinación de la producción
total y con estructura de los coeficientes técnicos y de los coeficientes
de costos se obtienen las demás variables de los otros dos enfoques,
por lo tanto, se muestra que en el agregado los tres PIB determinados
por las diferentes vías son iguales.
De igual manera, se estima los nuevos niveles de personal ocupado y
formación bruta de capital, haciendo uso de los coeficientes de estas
variables en el MIP de 1997, según la metodología expuesta en el capítulo V y basándose en el supuesto que no existe sustitución de personal ocupado y formación bruta de capital entre sectores, en el caso del
personal ocupado existe una oferta laboral amplia para que ante un
incremento de la producción se incremente los niveles de esta variable. Es bueno mencionar que estas variables se mueven en el mismo
sentido que la producción total, por consiguiente, para próximos trabajos, se puede analizar mejor el comportamiento de estas variables
dentro del Modelo Insumo-Producto. Por último es conveniente anotar, que los impuestos tipo IVA, subvenciones a los productos, impuesto a los productos y derechos de importación fueron estimados
exógenamente usando las participaciones de estas viables en la demanda final del año base, por otro lado estas son las que hacen que las
sumatoria de los Valores Agregados sectoriales (PIB sectorial total)
sean iguales al PIB total
157
158
6.909.439
7.840.669
7.403.220
8.401.001
7.336.352
8.325.120
FBCF
Personal Ocupado
39.203.458
65.950.707
30.204.441
22.110.841
8.093.600
2.394.736
(223.445)
695.030
590.870
41.662.617
70.025.600
32.120.963
23.623.099
8.497.864
2.561.738
(239.027)
743.500
691.770
41.943.151
70.663.859
32.414.462
23.763.305
8.651.157
2.557.739
(238.654)
742.339
632.330
PIB PRODUCCION
PB
PRODUCCION BRUTA (BÁSICOS)
CI
- CONSUMO INTERMEDIO
Bienes
Servicios
IMPUESTO TIPO IVA
IVA
SUB
SUBVENCIONES A LOS PRODUCTOS
IMP
IMPUESTO A LOS PRODUCTOS
DM
DERECHOS DE IMPORTACIÓN
39.203.458
13.453.794
10.215.700
3.238.094
408.545
(15.443)
15.259.757
4.547.641
162.584
1.929.388
2.394.736
(223.445)
695.030
590.870
41.662.617
13.957.461
10.599.444
3.358.018
433.842
(16.158)
16.427.201
4.826.338
172.869
2.103.084
2.561.738
(239.027)
743.500
691.770
1999
39.203.458
20.347.539
317.740
5.930.528
2.806.288
3.124.240
8.702.065
1.115.703
850
11.406.029
(8.616.996)
41.943.151
14.002.945
10.627.473
3.375.472
437.608
(16.687)
16.579.132
4.937.119
178.747
2.130.533
2.557.739
(238.654)
742.339
632.330
1998
41.662.617
21.267.821
318.617
5.756.633
2.724.002
3.032.631
10.414.832
1.208.204
1.017
12.783.979
(10.088.486)
PIB INGRESOS
RA
REMUNERACIONES
Sueldos y Salarios
SS
CS
Contribuciones Sociales
OIP
OTROS IMPUESTOS A LA PRODUCCIÓN
OSP
OTROS SUBSIDIOS A LA PRODUCCIÓN
EEN
EXCEDENTE NETO DE EXPLOTACIÓN
IMN
INGRESO MIXTO NETO
CCFNS
CONSUMO DE CAPITAL FIJO DE NO SOC
CCFS
CONSUMO DE CAPITAL FIJO DE SOC
IVA
IMPUESTOS TIPO IVA
SUB
SUBVENCIONES A LOS PRODUCTOS
IMP
IMPUESTO A LOS PRODUCTOS
DM
DERECHOS DE IMPORTACION
1997
41.943.151
21.277.403
332.672
5.675.828
2.685.766
2.990.062
10.685.198
920.488
1.043
12.272.151
(9.221.632)
PIB GASTO
CONSHOG CONSUMO DE LOS HOGARES
CONSISFL CONSUMO DE ISSFL
CONSGOB CONSUMO DEL GOBIERNO
Individual
Colectivo
FBCF
FBCF
VE
VE
ADQ. OBJETOS VALIOSOS
AOV
EXPORTACIONES
X
M
- Importaciones
7.030.696
7.978.269
40.237.806
67.108.110
30.552.549
22.304.553
8.247.996
2.506.904
(233.911)
727.585
681.667
40.237.806
13.830.703
10.497.921
3.332.783
416.682
(15.779)
15.543.809
4.647.826
164.763
1.967.556
2.506.904
(233.9
11)
727.585
681.667
40.237.806
21.127.311
307.224
6.228.860
2.947.457
3.281.403
8.796.478
1.681.652
859
12.036.569
(9.941.147)
2000
MIP
CONSTANTE
2001
7.279.755
8.260.896
41.865.159
69.485.385
31.598.490
23.031.581
8.566.909
2.691.473
(251.132)
781.153
756.770
41.865.159
14.454.521
10.974.678
3.479.843
432.624
(16.321)
15.902.441
4.880.940
171.530
2.061.161
2.691.473
(251.132)
781.153
756.770
41.865.159
22.145.894
293.994
6.628.013
3.136.334
3.491.679
9.993.585
1.915.166
976
11.923.943
(11.036.412)
2002
6.774.419
7.687.452
37.872.563
64.661.939
29.507.065
21.457.144
8.049.921
1.806.977
(168.603)
524.443
554.871
37.872.563
13.583.870
10.312.501
3.271.369
400.879
(15.562)
14.733.870
4.460.080
158.144
1.833.593
1.806.977
(168.603)
524.443
554.871
37.872.563
20.679.133
330.074
6.460.790
3.057.205
3.403.585
7.790.456
(291.656)
761
10.995.012
(8.092.007)
2003
5.986.136
6.792.927
33.794.704
57.137.769
25.874.157
18.573.448
7.300.708
1.742.092
(162.549)
505.612
445.936
33.794.704
12.473.548
9.466.585
3.006.963
356.581
(14.462)
12.834.089
3.943.278
139.077
1.531.500
1.742.092
(162.549)
505.612
445.936
33.794.704
19.758.931
332.795
6.374.796
3.016.513
3.358.283
4.759.517
(576.309)
465
9.647.852
(6.503.343)
00/99
01/00
-5,82%
-5,82%
1,75%
1,75%
3,54%
3,54%
-0,67% -5,90% 2,64% 4,04%
-0,90% -5,82% 1,75% 3,54%
-0,91% -5,97% 1,15% 3,42%
-0,59% -6,40% 0,88% 3,26%
-1,77% -4,76% 1,91% 3,87%
0,16% -6,52% 4,68% 7,36%
0,16% -6,52% 4,68% 7,36%
0,16% -6,52% 4,68% 7,36%
9,40% -14,59% 15,37% 11,02%
-0,90%
-0,90%
02/01
-6,94%
-6,94%
-9,54%
-6,94%
-6,62%
-6,84%
-6,03%
-32,86%
-32,86%
-32,86%
-26,68%
-9,54%
-6,02%
-6,03%
-5,99%
-7,34%
-4,65%
-7,35%
-8,62%
-7,80%
-11,04%
-32,86%
-32,86%
-32,86%
-26,68%
-5,90% 2,64% 4,04% -9,54%
-4,33% 3,83% 4,82% -6,62%
-0,28% -3,31% -4,31% 12,27%
3,02% 5,03% 6,41% -2,52%
3,02% 5,03% 6,41% -2,52%
3,02% 5,03% 6,41% -2,52%
-16,45% 1,08% 13,61% -22,05%
-7,66% 50,73% 13,89% -115,23%
-16,42% 1,06% 13,62% -22,03%
-10,78% 5,53% -0,94% -7,79%
-14,59% 15,37% 11,02% -26,68%
99/98
-0,67% -5,90% 2,64% 4,04%
-0,32% -3,61% 2,80% 4,51%
-0,26% -3,62% 2,76% 4,54%
-0,52% -3,57% 2,92% 4,41%
-0,86% -5,83% 1,99% 3,83%
-3,17% -4,42% 2,17% 3,44%
-0,92% -7,11% 1,86% 2,31%
-2,24% -5,77% 2,20% 5,02%
-3,29% -5,95% 1,34% 4,11%
-1,29% -8,26% 1,98% 4,76%
0,16% -6,52% 4,68% 7,36%
0,16% -6,52% 4,68% 7,36%
0,16% -6,52% 4,68% 7,36%
9,40% -14,59% 15,37% 11,02%
-0,67%
-0,05%
-4,22%
1,42%
1,42%
1,42%
-2,53%
31,26%
-2,49%
4,17%
9,40%
98/97
Var. %
Var. %
-11,64%
-11,64%
-10,77%
-11,64%
-12,31%
-13,44%
-9,31%
-3,59%
-3,59%
-3,59%
-19,63%
-10,77%
-8,17%
-8,20%
-8,08%
-11,05%
-7,07%
-12,89%
-11,59%
-12,06%
-16,48%
-3,59%
-3,59%
-3,59%
-19,63%
-10,77%
-4,45%
0,82%
-1,33%
-1,33%
-1,33%
-38,91%
97,60%
-38,90%
-12,25%
-19,63%
03/02
Cuadro 4. Los tres enfoques del Producto Interno Bruto
VI.6 Determinación de los sectores claves de la economía a partir del MIP
Aplicando los índices de eslabonamientos propuestos por Rasmussen
(1956) citado por Prem S. (1975, p. 63) y también usados en el trabajo
de Fernández (1994), se consideran los efectos directos como indirectos sobre la producción sectorial y agregada a partir del uso de la Inversa de Leontief, en la determinación de los sectores claves de una de
eslabonamiento intersectorial (hacia adelante y hacia atrás).
Cuadro 5. Índices de eslabonamiento intersectorial
ESLAB_ATRÁS
1
2
3
4
5
6
7
8
9
10
11
Agricultura, ganadePesca
Explotacion de MinIndustrias ManufSuministro de Construccion Comercio Hoteles y restauTransporte, AIntermediacionActividades in
A
B
C
D
E
F
G
H
I
J
K
Kj
1,91143
1,50711
1,37406
2,32532
1,53963
2,13202
1,80230
2,63453
1,81884
1,71476
1,41054
n
suma Kj
2
n
24,88435
Uj,b
0,9986
0,7873
0,7178
1,2148
0,8043
1,1138
0,9416
1,3763
0,9502
0,8958
0,7369
1
1,93975
2
1,02429
3
1,68933
4
6,69856
5
1,34953
6
1,28727
7
1,20101
8
1,08466
9
1,61091
10
2,45687
11
2,29863
0,5351
0,8825
3,4994
0,7050
0,6725
0,6274
0,5666
0,8416
1,2835
1,2008
ESLAB_ADELANTE
Ki
n
suma Ki
2
n
Ui,f
13
169
13
24,88435
169
1,0134
Ordenándolos:
Cuadro 5-A. Índices de eslabonamiento intersectorial ordenados
N_ACT
ACT
ESL_ATRAS
(Uj,b) N_ACT ACT
ESL_ADELANTE
3 Explotación de minas y canteras
0,71783
2 Pesca
11 Actividades inmobil. empresariales y de alquiler
0,73689
12 Administrac Pública y Defensa / Enseñanza / Salud
12 Administrac Pública y Defensa / Enseñanza / Salud 0,75307
8 Hoteles y restaurantes
2 Pesca
0,78734
13 Otras actividades
5 Suministro de electricidad, gas y agua
0,80433
7 Comercio
10 Intermediación financiera
0,89582
6 Construcción
7 Comercio
0,94155
5 Suministro de electricidad, gas y agua
9 Transporte,almacenamiento y comunicaciones
0,95019
9 Transporte,almacenamiento y comunicaciones
1 Agricultura, ganadería, caza y silvicultura
0,99856
3 Explotación de minas y canteras
6 Construcción
1,11380
1 Agricultura, ganadería, caza y silvicultura
4 Industrias manufactureras
1,21479
11 Actividades inmobil. empresariales y de alquiler
8 Hoteles y restaurantes
1,37632
10 Intermediación financiera
13 Otras actividades
1,70951
4 Industrias manufactureras
159
(Ui,f)
0,53511
0,54902
0,56664
0,62304
0,62743
0,67249
0,70502
0,84157
0,88253
1,01336
1,20084
1,28351
3,49944
Si se observa los índices de eslabonamiento hacia atrás, los sectores
que tienen los Uij > 1 son Construcción, Manufactura, Hoteles y
restaurantes y Otras actividades, esto indica que los cambios en la
producción del resto de los sectores o actividades, depende en mayor
medida de cambios en la demanda final de estos, es decir, que estas
industrias tienen mayor capacidad para mover la producción de todos
los demás sectores, ante cambios exógenos en la demanda final de
estos sectores, por lo tanto tienen una mayor capacidad de encadenamiento hacia atrás o de integración vertical.
Por otro lado, los índices de eslabonamiento hacia adelante, Ui f > 1,
nos muestran que aplican sólo para Agricultura, ganadería, caza y silvicultura, Actividades inmobiliarias, empresariales y de alquiler, Intermediación financiera e Industrias Manufactureras, por lo tanto, todos
ellos mueven su producción rápidamente para satisfacer los cambios
exógenos en la demanda final de los demás sectores. Por consiguiente,
si se encontrara un sólo sector cuyo índice de eslabonamiento hacia
delante fuese mayor que uno, los cambios en la demanda final del resto
de los sectores ejercerían una influencia mayor sobre la producción de
este sector; y a groso modo, esta industria podría incrementar su producción más que el resto de los sectores por unidad de incremento en
la demanda final en todos los sectores, es decir, tienen una mayor capacidad de encadenamiento hacia adelante o de integración horizontal.
De allí se muestra que el sector clave es aquel en que simultáneamente,
los índices de eslabonamientos hacia atrás y hacia adelante (Uj b y Uif)
son mayores que uno (Industria manufacturera), es decir, poseen un
mayor encadenamiento tanto hacia adelante como hacia atrás. Esto
sucede en la apertura de 13 productos por 13 actividades, de allí pues,
se tendrían que evaluar estos índices en matrices Insumo-Producto más
desagregados para determinar cuáles dentro de esta agregación son las
actividades que dinamizan el proceso productivo de la economía, de
igual manera probar la extensión de estos índices con los propuestos
en el trabajo de Clemente y Puente (1989) sobre los índices de dispersión de la distribución del encadenamiento.
160
En atención a lo planteado en los índices de encadenamiento, se observa que el sector clave, es decir, aquel donde los índices de eslabonamiento son mayores que uno es Manufactura (gráfico 4). Por lo tanto,
si se interpreta el eslabonamiento hacia atrás, se observa que el sector clave requiere insumos de otros sectores por encima del promedio,
por consiguiente, existe una alta probabilidad de inversión en los sectores oferentes (expandir la producción de bienes para el consumo intermedio y/o un mecanismo para la protección de los sectores nacionales) y con respecto al eslabonamiento hacia adelante, el mecanismo
es menos directo pero depende de la probabilidad de inversión en sectores en los cuales el producto del sector estratégico sea insumo importante.
Gráfico 4. Determinación de los sectores claves
1
2
3
3,4994
4
1,2148
5
0,6725
S e c to r e s
6
1,1138
7
0,5666
8
1,3763
9
10
11
12
0,6230
13
0,0000
1,7095
0,5000
1,0000
1,5000
2,0000
2,5000
Indic es
Uj,b
161
U i,f
3,0000
3,5000
CONCLUSIÓN
El Modelo Insumo-Producto (MIP) enfocado desde el punto de vista
estático, permite determinar los niveles de producción que alcanzarán
los diferentes sectores o industrias para satisfacer los cambios exógenos
en la demanda final; en este sentido, se puede constatar que este modelo es de gran utilidad en la planificación de la producción, del empleo y en la determinación de las estructuras encadenantes del proceso
productivo denominado sectores claves. Bajo esta perspectiva, crea
condiciones mínimas o bases para desarrollar otros estudios relacionados con modelos de equilibrio general computable, análisis de las condiciones estructurales de una economía, redes sociales, modelos
Insumo-Producto dinámicos, matrices de contabilidad social, estudios
econométricos y análisis de multiplicadores multisectoriales.
Por otra parte, se han presentado las bases metodológicas para la construcción de matrices Insumo-Producto a partir de los Cuadros de Oferta y Utilización (COU) para la economía venezolana, cuyos datos son
obtenidos del Programa de Actualización de la Estimaciones
Macroeconómicas (Pracem) e implementación del nuevo año base 1997,
de allí pues, que se incorporó también los diferentes métodos para
resolver la presencia de productos secundarios y no quebrantar el supuesto básico del MIP que es la homogeneidad en la función de producción.
Los resultados obtenidos, dan consistencia a la importancia del análisis y evaluación de la producción secundaria como elemento fundamental para la construcción del Modelo Insumo-Producto, por otro
lado, la presente investigación y los ejercicios con datos consistentes
de la economía venezolana hacen válido la interpretación de las estructuras productivas de Venezuela para el año 1997, dado que el Cuadro de Oferta y Utilización ha sido base para la construcción del circuito económico y los flujos intrasectoriales e intersectoriales de MIP.
Por consiguiente, se debe destacar, que este trabajo cuenta con una
162
gran visión metodológica y analítica, para mejorar el análisis InsumoProducto y ampliar la posibilidad de seguir indagando sobre las estructuras productivas de la economía venezolana.
Asimismo, puede concluirse que el supuesto básico de esta investigación ha sido verificado, con relación a que el MIP permite anticipar la
dirección del cambio en el PIB sectorial total, a pesar de la existencia
de sectores donde no se movieron en la dirección (observada), pero
los cambios no fueron lo suficientemente grandes como para cambiar
la dirección del agregado. Bajo este enfoque, se abre la posibilidad de
revisar cuáles son las actividades dentro de cada sector, que anticipan
o no la dirección del cambio la producción sectorial, para estos casos,
se deben usar las diferentes tablas de concatenación (productos-actividades) para construir matrices Insumo-Producto más desagregadas.
En este mismo orden de ideas, la identificación de los sectores claves
es otra parte primordial de la evaluación del MIP, dado que en él se
muestran cuáles industrias al mover su demanda final podrían incrementar la producción del resto de los sectores (encadenamientos hacia
atrás), y cuáles sectores son los más vulnerables a la variación de su
producción por variaciones expresadas en la demanda final del resto
de los sectores (encadenamientos hacia delante). Por consiguiente, al
existir coincidencia para una industria entre los dos tipos de encadenamiento, estamos en presencia de una actividad estratégica, a la cual, se
le debe dar apoyo y estímulo a través de políticas industriales y sectoriales.
En atención a lo anteriormente planteado, se pretende demostrar la
importancia de contar con Matrices Insumo-Producto para diferentes
años, tanto en términos corrientes, constantes y de implícitos de precios, ya que permite la actualización de las funciones de producción,
posibilita el mejoramiento de las mediciones del PIB y de las
interrelaciones entre los sectores productivos. De igual manera, se puede
determinar como los impactos de los choques tecnológicos afectan a la
producción, al comportamiento en las formas de consumo, aparición y
163
desaparición de productos, cambios en la forma de organización de los
mercados, la ejecución de determinados regímenes de política económica. Visto de esta forma, estos fenómenos descritos repercuten en el
nivel y relación de precios de la economía nacional y sobre la estructura de los precios relativos de los bienes y servicios producidos por las
distintas actividades económicas, en este sentido, pueden dar indicios
para determinar la obsolescencia del año base seleccionado y determinar condiciones para la implementación de un nuevo año base.
164
APÉNDICE
Cuadro 1
Concatenación de Productos y Actividades para construcción
de cuadros simétricos de Insumo-Producto (primera agregación)
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A001
A002
A002
A002
A002
A002
A002
A003
A003
A003
A003
A003
A003
A003
A003
A003
A004
A004
A004
A005
A005
A005
A005
A005
A006
A006
A007
A007
A007
A008
A008
A009
A009
A009
A009
TRANSACCIONES / PRODUCTOS
CONCEPTO
Arroz
Maíz
Sorgo
Otros cereales
Caraotas
Frijol
Otros granos leguminosos
Papa
Yuca
Otras raíces y tubérculos
Ajonjolí
Algodón
Otros productos textiles y oleaginosos
Caña de Azúcar
Tabaco
Otros Cultivos
Tomate
Cebolla
Ajo
Pimentón
Zanahoria
Otras hortalizas, legumbres, viveros y flores
Cambur
Plátano
Naranjas
Piña
Nueces, almendras y avellanas a granel
Otras frutas
Café
Cacao
Otras plantas para bebidas y especies
Ganado bovino
Resto de animales vivos (Chivo, Cabra, Oveja, Corderos)
Leche cruda
Ganado porcino
Aves
Otros animales, n.c.p. (Pato, Pavo, Lapa)
Huevos de consumo
Otros productos animales, n.c.p.
Servicios relacionados con la agricultura
Servicios relacionados con la ganadería
Fundación de plantaciones agrícolas
Fundación de plantaciones forestales
Mejoras agrícolas (Pastizales, Deforestación y Otros)
Productos Forestales
Otros Productos de la silvicultura y servicios conexos
Atún
Pargo
Mero
Carite
165
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
A009
A009
A009
A009
A010
A010
A011
A011
A012
A013
A014
A015
A015
A015
A015
A015
A016
A016
A016
A016
A017
A018
A019
A019
A020
A020
A020
A020
A020
A021
A022
A023
A024
A024
A024
A024
A025
A025
A025
A025
A025
A025
A026
A027
A027
A028
A028
A029
A030
A031
TRANSACCIONES / PRODUCTOS
CONCEPTO
Sardinas frescas
Otros pescados frescos o refrigerados
Camarones frescos
Otros crustáceos sin congelar, vivos, frescos o refrigerados
Carbón
Lignito y turba
Petróleo crudo
Gas natural
Servicios vinculados con la extraccion de petróleo
Minerales de Uranio y Torio
Minerales de hierro
Minerales de aluminio (Bauxita)
Oro
Otros Metales Preciosos
Minerales de níquel
Otros Minerales Metálicos No Ferrosos
Granito y otras piedras de construcción
Piedra caliza, yeso y otros
Arenas, grava, piedra partida y otros
Arcillas
Minerales para Abonos y productos químicos
Sal
Diamante y otras piedras preciosas
Otros minerales
Carne de ganado bovino fresca, refrigerada o congelada
Carne de ganado porcino fresca, refrigerada o congelada
Carne de otros animales (Chivo, Cordero, etc.)
Carne de aves
Preparados y Conservas de Carnes y Productos de Carne
Pescados y Crustáceos enlatados, salados y ahumados
Conservas y Preparados de Frutas, Legumbres y Hortalizas
Aceites y grasas de origen animal y vegetal
Mantequillas y quesos
Leche Pasteurizada
Leche en Polvo
Otros productos lácteos
Harina de trigo
Harina de maíz
Arroz descascarado
Productos de Cereales
Aceite de maíz
Resto de Productos de Molinería (Incluye Casabe)
Alimentos para animales
Pan
Resto de productos de panadería
Azúcar
Resto de Productos de Azúcar y Derivados (Incluye Papelón)
Cacao, chocolate y productos de confitería
Pastas Alimenticias
Café y preparados de té
166
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
A031
A032
A032
A032
A033
A033
A034
A034
A035
A036
A037
A038
A039
A040
A041
A042
A043
A044
A044
A044
A045
A045
A045
A045
A045
A046
A047
A047
A047
A047
A047
A047
A048
A049
A050
A051
A052
A053
A054
A055
A055
A056
A057
A057
A058
A058
A058
A059
A059
A060
TRANSACCIONES / PRODUCTOS
CONCEPTO
Resto de otros productos alimenticios
Whisky
Cervezas
Resto de Bebidas Alcohólicas
Bebidas gaseosas
Resto de bebidas no alcohólicas
Cigarrillo
Resto de productos de tabaco
Hilatura y tejedura de productos textiles
Otros productos textiles
Tejidos y artículos de punto o ganchillo
Prendas de vestir, excepto prendas de piel
Adobo y teñido de pieles; artículos de piel
Artículos de cuero
Calzado
Madera Aserrada
Productos de madera, corcho, paja y materiales trenzables
Pasta de madera, papel y cartón
Envases y productos de Papel y cartón ondulado
Otros artículos de papel y cartón
Libros, folletos, partituras y otras publicaciones
Periódicos, revistas y publicaciones periódicas
Grabaciones y otros productos de edición
Impresión (Imprentas)
Reproducción de grabaciones
Productos de carbón
Gasolina
Gasóleos y destilados
Residuales (fuel oil)
Lubricantes
Gas líquido de petróleo (GLP)
Otros Productos de Petróleo Refinado
Sustancias Químicas Básicas
Abonos y compuestos de nitrógeno
Plásticos en formas primarias y de caucho sintético (polímeros)
Plaguicidas y otros productos químicos de uso agropecuario
Pinturas, barnices y lacas
Productos farmacéuticos, sustancias químicas medicinales y productos botánicos
Jabones y detergentes, preparados para limpiar y pulir, perfumes y preparados de tocador
Sal refinada
Otros productos químicos n.c.p.
Hilados y telas sintéticas
Llantas y cámaras de caucho
Otros productos de caucho
Tubos y otros de plástico
Bolsas, envases y otros productos de material plástico
Otros productos de plástico
Vidrio y fibras de vidrio, vidrios para carros
Envases, botellas y otros de vidrio común
Objetos y vasijas de barro, loza, porcelana y cerámica
167
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
A061
A062
A063
A063
A064
A065
A065
A066
A066
A066
A066
A067
A067
A067
A067
A067
A068
A068
A069
A069
A069
A070
A071
A071
A072
A072
A073
A074
A074
A074
A075
A075
A075
A075
A075
A075
A076
188
A076
189
A076
190
191
192
193
194
195
196
197
198
199
200
A077
A077
A077
A078
A078
A078
A078
A079
A079
A080
A080
TRANSACCIONES / PRODUCTOS
CONCEPTO
Productos de cerámica refractaria
Productos de arcilla, cerámica refractaria y no refractaria para uso estructural
Cemento
Cal y yeso
Artículos de hormigón, cemento y yeso
Asfalto sólido para pavimentos
Resto de productos a base de asfalto, n.c.p.
Productos semielaborados de hierro o acero
Productos planos de hierro o acero
Productos no planos de hierro o acero
Resto de productos de hierro o acero, n.c.p.
Oro fundido y refinado
Productos planos de aluminio
Productos no planos de aluminio
Alúmina
Resto de productos primarios de metales preciosos y metales no ferrosos
Productos de hierro y acero
Productos de metales no ferrosos
Estructuras y construcciones mayores metálicas
Tanques, depósitos y recipientes de metal
Generadores de vapor excepto calderas de agua caliente para calefacción central
Otros productos elaborados de metal
Motores, Turbinas, Bombas, Compresores
Otros tipos de maquinarias de uso general, sus partes y piezas
Maquinaria para la explotación de minas, y canteras y para obras de construcción
Resto de maquinaria y equipo de uso especial
Aparatos de uso doméstico n.c.p.
Máquinas de procesamiento automático de datos
Máquinas impresoras
Resto de maquinaria de oficina; Contabilidad e informática, partes, piezas y accesorios
Motores, generadores y transformadores eléctricos, partes y piezas
Aparatos de distribución y control de la energía eléctrica, sus partes y piezas
Hilos y cables aislados
Acumuladores y pilas y baterías primarias, partes y piezas
Lámparas eléctricas y equipo de iluminación, partes y piezas
Otros tipos de equipos eléctricos n.c.p., partes y piezas
Tubos y válvulas electrónicas y de otros componentes electrónicos, partes y piezas
Transmisores de radio y televisión y aparatos para telefonía y telegrafía con hilos, partes y piezas
Receptores de radio y televisión, aparatos de grabación y reproducción de sonido y video y productos
conexos
Aparatos e instrumentos médicos; para medir, ensayar, verificar y otros fines; partes, piezas y
accesorios
Instrumentos de óptica y equipo fotográfico; partes, piezas y accesorios
Relojes; sus partes y piezas
Automóviles para pasajeros
Resto de vehículos automotores
Carrocerías para vehículos automotores, de remolques y semiremolques; y sus partes y piezas
Partes, piezas y accesorios para vehículos automotores y sus motores
Buques y otras embarcaciones
Otros tipos de equipos de transporte n.c.p.
Muebles
Productos manufacturados n.c.p.
168
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
A081
A082
A083
A084
A085
A085
A086
A086
A086
A086
A086
A086
A086
A086
A086
A086
A086
CONCEPTO
Desperdicios y Desechos
Electricidad
Gas
Agua
Construcción de edificios residenciales de una y dos viviendas
Construcción de edificios residenciales multifamiliar
Construcción de almacenes y edificaciones para la manufactura
Construcción de edificaciones comerciales
Construcción de edificaciones para deportes y esparcimiento
Construcción de hoteles, restaurantes y edificaciones análogos
Construcción de edificaciones para la enseñanza
Construcción de edificaciones relacionados con la salud pública
Construcciones de obras de vialidad
Construcciones de obras hidráulicas
Construcciones de líneas de comunicación y energía eléctrica
Construcciones para la industria petrolera
Otras obras de construcción, n.c.p.
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
A087
A088
A089
A090
A091
A092
A093
A094
A095
A095
A096
A096
A096
A096
A096
A096
A097
A098
A098
A099
A099
A100
A101
A101
A101
A101
A101
A101
A102
A103
A104
A105
A105
Servicios de Alquiler de equipo de construcción o demolición de edificios para trabajos de ingeniería
Obras de Urbanismo
Servicios de Comercio al Por Mayor
Servicios de Comercio al Detal
Servicios de Mantenimiento y Reparación de Vehículos Automotores y Motocicletas
Servicios de Reparación de Efectos Personales y Enseres Domésticos
Servicios de Hotelería
Servicios de Restaurantes, Bares y Similares
Servicios de Transporte de pasajeros por vía férrea
Servicios de Transporte de carga por vía férrea
Servicios de Transporte en metro, metrobús
Resto de otros tipos de Servicios de transporte regular de pasajeros por vía terrestre
Servicios de Transporte no regular de pasajeros por vía terrestre
Servicios de Transporte regular de carga por vía terrestre
Servicios de Transporte no regular de carga por vía terrestre
Servicio de alquiler de vehículos comerciales con conductor
Servicios de transporte por tuberías de petróleo y gas natural
Servicios de transporte de Pasajeros por agua
Servicios de transporte de Carga por agua
Servicios de transporte de Pasajeros por vía Aérea
Servicios de transporte de Carga por vía Aérea
Servicios de almacenamiento y depósito
Servicios de estaciones de autobuses (terminales de pasajeros)
Servicios de explotación de carreteras, puentes y túneles (peajes)
Servicios de estacionamiento
Servicios de puertos y vías de navegación
Servicios complementarios del transporte aéreo
Servicios complementarios del transporte por agua
Servicios de agencias de viajes y turismo
Servicio Agencias de Aduanas y Otros Servicios de Agencias de Transporte
Servicios postales y de correo
Servicio de Telefonía Básica
Servicio de Telefonía Celular
TRANSACCIONES / PRODUCTOS
169
NOMENCLATURA
DE PRODUCTOS
Cód. Activ.
CODPROD
CODACT
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
A105
A105
A105
A106
A106
A107
A107
A107
A108
A108
A108
A109
A109
A109
A109
A110
A110
A111
A111
A112
271
272
273
274
275
276
277
A113
A114
A114
A115
A116
A117
A118
278
279
280
281
282
283
284
285
286
287
288
289
A118
A118
A118
A118
A119
A120
A121
A121
A121
A122
A122
A122
CONCEPTO
Servicios de transmisión de datos y mensajes
Servicios de radio y televisión por cable
Otros servicios de telecomunicaciones
Servicios de Banca Central
Servicios de Otras Instituciones de Intermediación Monetaria
Arrendamiento financiero
Otros servicios de concesión de crédito
Otros servicios de intermediación financiera n.c.p.
Servicios de seguros de vida
Planes de pensiones y rentas vitalicias
Servicios de seguros generales
Servicios de Administración de mercados financieros
Servicios de Mercado de Valores (Bursátiles)
Servicios de Consultores Financieros
Otros servicios auxiliares de la intermediación financiera
Servicios de Corretaje de seguros
Otros servicios Auxiliares de seguros y financiación de pensiones
Servicios de viviendas Arrendadas
Servicio de Viviendas Habitadas por el propietario (imputación)
Servicios de alquiler de inmuebles no residenciales
Servicios inmobiliarias por comisión o contrato; incluyendo compra-venta de inmuebles (Empresas
Inmobiliarias)
Servicios de Alquiler de Medios de Transporte
Servicios de Alquiler de otros tipos de maquinaria y equipo
Servicios de Alquiler de efectos personales y enseres domésticos n.c.p.
Servicios de Informática y Servicios Conexos
Servicios de Investigación y Desarrollo
Servicios jurídicos
Servicios de Contabilidad y Auditoría Y Teneduría de libros; Asesoramiento Tributario, Encuestas de
Opinión Pública y Asesoramiento Empresarial
Servicios de Arquitectura e Ingeniería y otras actividades técnicas
Servicios de publicidad
Otros Servicios Empresariales n.c.p.
Servicios de la Administración Pública y Defensa
Servicios de Seguridad Social de Afiliación Obligatoria
Servicios de enseñanza primaria y secundaria
Servicios de enseñanza superior
Otros tipos de enseñanza, n.c.p.
Servicios de hospitales, clínicas y laboratorios
Servicios médicos y odontológicos particulares
Otros servicios sociales y de salud
290
291
292
293
294
295
296
297
298
299
300
A123
A124
A124
A125
A125
A125
A125
A126
A126
A126
A127
Servicios de Eliminación de Desperdicios y Aguas Residuales, Saneamiento y Actividades similares
Servicios de Organizaciones Empresariales y de Empleadores en General
Servicios de Organizaciones Profesionales, Sindicatos y Otras Asociaciones no Lucrativas
Servicios de Cine y similares
Servicios de Radio y Televisión
Otros servicios de entretenimiento n.c.p.
Servicios Culturales, Deportivos y Otros Servicios de Esparcimiento
Servicios de peluquería y otros tratamientos de belleza
Servicios Funerarios y Actividades Conexas
Otros Servicios n.c.p.
Servicio Doméstico
TRANSACCIONES / PRODUCTOS
170
Cuadro 2
Concatenación de Productos, Actividades y Clasificación
de 2 Dígitos de la CIIU (División) para construcción
de cuadros simétricos de Insumo-Producto (Segunda
agregación)
F IL A
COLUMNA
PRODUCTO
ACTIVIDAD
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
044
045
046
047
048
049
050
001
001
001
001
001
001
001
001
001
001
001
001
001
001
001
001
002
002
002
002
002
002
003
003
003
003
003
003
003
003
003
004
004
004
005
005
005
005
005
006
006
007
007
008
008
009
009
009
009
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
02
02
05
05
05
05
DESCRIPCIÓN CIIU 2 DIG
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Agricultura, Ganadería Caza y Actividades de Servicios Conexas
Silvicultura Extracción de Madera y Actividades de Servicios Conexas
Silvicultura Extracción de Madera y Actividades de Servicios Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
171
FILA
COLUMNA
PRODUCTO
ACTIVIDAD
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
009
009
009
009
010
010
011
011
012
013
014
015
015
015
015
015
016
016
016
016
017
018
019
019
020
020
020
020
020
021
022
023
024
024
024
024
025
025
025
025
025
025
026
027
027
028
028
029
030
031
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
05
05
05
05
10
10
11
11
11
12
13
13
13
13
13
13
14
14
14
14
14
14
14
14
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
DESCRIPCIÓN CIIU 2 DIG
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Pesca, Explotación de Criaderos de Peces y Granjas Piscícolas, Actividades de Servicos Conexas
Extracción de Carbón y Lignito: Extracción de Turba
Extracción de Carbón y Lignito: Extracción de Turba
Extracción de Petróleo crudo y Gas Natural, Actividades de Servicios Relacionada
Extracción de Petróleo crudo y Gas Natural, Actividades de Servicios Relacionada
Extracción de Petróleo crudo y Gas Natural, Actividades de Servicios Relacionada
#N/A
Extracción de Minerales Metalíferos
Extracción de Minerales Metalíferos
Extracción de Minerales Metalíferos
Extracción de Minerales Metalíferos
Extracción de Minerales Metalíferos
Extracción de Minerales Metalíferos
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Explotación de otras Minas y Canteras
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
172
FILA
COLUMNA
PRODUCTO
ACTIVIDAD
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
031
032
032
032
033
033
034
034
035
036
037
038
039
040
041
042
043
044
044
044
045
045
045
045
045
046
047
047
047
047
047
047
048
049
050
051
052
053
054
055
055
056
057
057
058
058
058
059
059
060
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
15
15
15
15
15
15
16
16
17
17
17
18
18
19
19
20
20
21
21
21
22
22
22
22
22
23
23
23
23
23
23
23
24
24
24
24
24
24
24
24
24
24
25
25
25
25
25
26
26
26
DESCRIPCIÓN CIIU 2 DIG
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos Alimenticios y Bebidas
Elaboración de Productos de Tabaco
Elaboración de Productos de Tabaco
Fabricación de Textiles
Fabricación de Textiles
Fabricación de Textiles
Fabricación de Prendas de Vestir, Adobo y Teñido de Pieles
Fabricación de Prendas de Vestir, Adobo y Teñido de Pieles
Curtido y Adobo de Cueros, Fabricación de Maletas, Bolsos de Mano.
Curtido y Adobo de Cueros, Fabricación de Maletas, Bolsos de Mano.
Producción de Madera y Fabricación de Productos de Madera y Corcho, excepto Muebles
Producción de Madera y Fabricación de Productos de Madera y Corcho, excepto Muebles
Fabricación de Papel y Productos de Papel
Fabricación de Papel y Productos de Papel
Fabricación de Papel y Productos de Papel
Actividades de Edición e Impresión y de Reproducción de Grabaciones
Actividades de Edición e Impresión y de Reproducción de Grabaciones
Actividades de Edición e Impresión y de Reproducción de Grabaciones
Actividades de Edición e Impresión y de Reproducción de Grabaciones
Actividades de Edición e Impresión y de Reproducción de Grabaciones
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Coque, Productos de la Refinación del Petróleo y Combustible
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Substancias y Productos Químicos
Fabricación de Productos de Caucho y Plástico
Fabricación de Productos de Caucho y Plástico
Fabricación de Productos de Caucho y Plástico
Fabricación de Productos de Caucho y Plástico
Fabricación de Productos de Caucho y Plástico
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
173
FILA
COLUMNA
PRODUCTO
ACTIVIDAD
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
061
062
063
063
064
065
065
066
066
066
066
067
067
067
067
067
068
068
069
069
069
070
071
071
072
072
073
074
074
074
075
075
075
075
075
075
076
076
CÓDIGO
CIIU 2 DIG
26
26
26
26
26
26
26
27
27
27
27
27
27
27
27
27
27
27
28
28
28
28
29
29
29
29
29
30
30
30
31
31
31
31
31
31
32
32
MATRIZ CUADRADA
189
076
32
Fabricación de Equipos y Aparatos de Radio Televisión y Comunicaciones
190
077
33
Fabricación de Instrumentos Médicos, Opticos y de Precisión; Fabricación de Reloj
191
192
193
194
195
196
197
198
199
200
077
077
078
078
078
078
079
079
080
080
33
33
34
34
34
34
35
35
36
36
Fabricación de Instrumentos Médicos, Opticos y de Precisión; Fabricación de Reloj
Fabricación de Instrumentos Médicos, Opticos y de Precisión; Fabricación de Reloj
Fabricación de Vehículos Automotores, Remolques y Semi-Remolques
Fabricación de Vehículos Automotores, Remolques y Semi-Remolques
Fabricación de Vehículos Automotores, Remolques y Semi-Remolques
Fabricación de Vehículos Automotores, Remolques y Semi-Remolques
Fabricación de otros Tipos de Equipo de Transporte
Fabricación de otros Tipos de Equipo de Transporte
Fabricación de Muebles; Industria Manufacturera Ncp
Fabricación de Muebles; Industria Manufacturera Ncp
DESCRIPCIÓN CIIU 2 DIG
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Productos Minerales No Metálicos
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de otros Metales Comunes
Fabricación de Productos elaborados de Metal, excepto Maquinaria y Equipo
Fabricación de Productos elaborados de Metal, excepto Maquinaria y Equipo
Fabricación de Productos elaborados de Metal, excepto Maquinaria y Equipo
Fabricación de Productos elaborados de Metal, excepto Maquinaria y Equipo
Fabricación de Maquinaria y Equipo
Fabricación de Maquinaria y Equipo
Fabricación de Maquinaria y Equipo
Fabricación de Maquinaria y Equipo
Fabricación de Maquinaria y Equipo
Fabricación de Maquinaria de oficina, Contabilidad e Informática
Fabricación de Maquinaria de oficina, Contabilidad e Informática
Fabricación de Maquinaria de oficina, Contabilidad e Informática
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Maquinaria y Aparatos eléctricos
Fabricación de Equipos y Aparatos de Radio Televisión y Comunicaciones
Fabricación de Equipos y Aparatos de Radio Televisión y Comunicaciones
174
FILA
COLUMNA
PRODUCTO
ACTIVIDAD
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
081
082
083
084
085
085
086
086
086
086
086
086
086
086
086
086
086
087
CÓDIGO
CIIU 2 DIG
37
40
40
41
45
45
45
45
45
45
45
45
45
45
45
45
45
45
MATRIZ CUADRADA
219
220
221
222
220
221
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
088
089
090
091
089
090
092
093
094
095
095
096
096
096
096
096
096
097
098
098
099
099
100
101
101
101
101
101
101
102
103
104
105
105
45
50
50
50
51
52
52
55
55
60
60
60
60
60
60
60
60
60
61
61
62
62
63
63
63
63
63
63
63
63
63
64
64
64
DESCRIPCIÓN CIIU 2 DIG
Reciclamiento
Suministros de electricidad, Gas Vapor y Agua Caliente
Suministros de electricidad, Gas Vapor y Agua Caliente
Captación, Depuración y Distribución de Agua
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Construcción
Venta, Mantenimiento y Reparación de Vehículos Automotores y Motocicletas; Venta
Venta, Mantenimiento y Reparación de Vehículos Automotores y Motocicletas; Venta
Venta, Mantenimiento y Reparación de Vehículos Automotores y Motocicletas; Venta
Comercio al Por Mayor y en Comisión, excepto el Comercio de Vehículos Automotores
Comercio al Por Menor, excepto el Comercio de Vehículos Automotores y Motocicleta
Comercio al Por Menor, excepto el Comercio de Vehículos Automotores y Motocicleta
Hoteles y Restaurantes
Hoteles y Restaurantes
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía terrestre; Transporte por tuberías
Transporte por vía acuática
Transporte por vía acuática
Transporte por vía aérea
Transporte por vía aérea
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Actividades de Transporte Complementarias y Auxiliares, Actividades de Agencias
Correo y Telecomunicaciones
Correo y Telecomunicaciones
Correo y Telecomunicaciones
175
FILA
COLUMNA
PRODUCTO
ACTIVIDAD
251
252
253
254
255
256
257
258
259
260
261
262
263
265
266
267
268
269
270
105
105
105
106
106
107
107
107
108
108
108
109
109
109
110
110
111
111
112
CÓDIGO
CIIU 2 DIG
64
64
64
65
65
65
65
65
66
66
66
67
67
67
67
67
70
70
70
MATRIZ CUADRADA
271
272
273
274
275
276
277
113
114
114
115
116
117
118
70
71
71
71
72
73
74
Actividades Inmobiliarias
Alquiler de Maquinaria y Equipos sin Operarios y de Efectos Personales y Enseres
Alquiler de Maquinaria y Equipos sin Operarios y de Efectos Personales y Enseres
Alquiler de Maquinaria y Equipos sin Operarios y de Efectos Personales y Enseres
Informática y Actividades Conexas
Investigación y Desarrollo
Otras Actividades Empresariales
278
279
280
281
282
283
284
285
286
287
288
289
118
118
118
118
119
120
121
121
121
122
122
122
74
74
74
74
75
75
80
80
80
85
85
85
Otras Actividades Empresariales
Otras Actividades Empresariales
Otras Actividades Empresariales
Otras Actividades Empresariales
Administración Publica y Defensa; Planes de Seguridad Social de Afiliación Obligatoria
Administración Publica y Defensa; Planes de Seguridad Social de Afiliación Obligatoria
Enseñanza
Enseñanza
Enseñanza
Servicios Sociales y de Salud
Servicios Sociales y de Salud
Servicios Sociales y de Salud
290
291
292
293
294
295
296
297
298
299
300
123
124
124
125
125
125
125
126
126
126
127
90
91
91
92
92
92
92
93
93
93
95
Eliminación de Desperdicios y Aguas Residuales, Saneamiento y Actividades Similares
Actividades de Asociaciones Ncp
Actividades de Asociaciones Ncp
Actividades de Esparcimiento y Actividades Culturales y Deportivas
Actividades de Esparcimiento y Actividades Culturales y Deportivas
Actividades de Esparcimiento y Actividades Culturales y Deportivas
Actividades de Esparcimiento y Actividades Culturales y Deportivas
Otras Actividades de Servicios
Otras Actividades de Servicios
Otras Actividades de Servicios
Hogares Privados con Servicio Doméstico
DESCRIPCIÓN CIIU 2 DIG
Correo y Telecomunicaciones
Correo y Telecomunicaciones
Correo y Telecomunicaciones
Intermediación Financiera; excepto el Financiamiento de Planes de Seguros y Pensiones
Intermediación Financiera; excepto el Financiamiento de Planes de Seguros y Pensiones
Intermediación Financiera; excepto el Financiamiento de Planes de Seguros y Pensiones
Intermediación Financiera; excepto el Financiamiento de Planes de Seguros y Pensiones
Intermediación Financiera; excepto el Financiamiento de Planes de Seguros y Pensiones
Financiamiento de Planes de Seguro y de Pensiones, excepto los Planes de Seguridad
Financiamiento de Planes de Seguro y de Pensiones, excepto los Planes de Seguridad
Financiamiento de Planes de Seguro y de Pensiones, excepto los Planes de Seguridad
Actividades Auxiliares de la Intermediación Financiera
Actividades Auxiliares de la Intermediación Financiera
Actividades Auxiliares de la Intermediación Financiera
Actividades Auxiliares de la Intermediación Financiera
Actividades Auxiliares de la Intermediación Financiera
Actividades Inmobiliarias
Actividades Inmobiliarias
Actividades Inmobiliarias
176
Cuadro 3
Concatenación de Productos, Actividades, Clasificación
de 2 Dígitos de la CIIU (División) y Clasificación de 1 Dígito de
la CIIU (Catálogo) para construcción de cuadros simétricos
de Insumo-Producto (tercera agregación)
FILA
PRODUCTO
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
044
045
046
047
048
049
050
COLUMNA
ACTIVIDAD
001
001
001
001
001
001
001
001
001
001
001
001
001
001
001
001
002
002
002
002
002
002
003
003
003
003
003
003
003
003
003
004
004
004
005
005
005
005
005
006
006
007
007
008
008
009
009
009
009
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
02
02
05
05
05
05
CÓDIGO
CIIU 1 DIG
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
B
B
B
B
177
DESCRIPCIÓN
CIIU 1 DIG
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Agricultura, ganaderia, caza y silvicultura
Pesca
Pesca
Pesca
Pesca
FILA
PRODUCTO
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
COLUMNA
ACTIVIDAD
009
009
009
009
010
010
011
011
012
013
014
015
015
015
015
015
016
016
016
016
017
018
019
019
020
020
020
020
020
021
022
023
024
024
024
024
025
025
025
025
025
025
026
027
027
028
028
029
030
031
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
05
05
05
05
10
10
11
11
11
12
13
13
13
13
13
13
14
14
14
14
14
14
14
14
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
CÓDIGO
CIIU 1 DIG
B
B
B
B
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
178
DESCRIPCIÓN
Pesca
Pesca
Pesca
Pesca
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Explotacion de Minas y Canteras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
CIIU 1 DIG
FILA
PRODUCTO
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
COLUMNA
ACTIVIDAD
031
032
032
032
033
033
034
034
035
036
037
038
039
040
041
042
043
044
044
044
045
045
045
045
045
046
047
047
047
047
047
047
048
049
050
051
052
053
054
055
055
056
057
057
058
058
058
059
059
060
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
15
15
15
15
15
15
16
16
17
17
17
18
18
19
19
20
20
21
21
21
22
22
22
22
22
23
23
23
23
23
23
23
24
24
24
24
24
24
24
24
24
24
25
25
25
25
25
26
26
26
CÓDIGO
CIIU 1 DIG
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
179
DESCRIPCIÓN
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
CIIU 1 DIG
FILA
PRODUCTO
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
COLUMNA
ACTIVIDAD
061
062
063
063
064
065
065
066
066
066
066
067
067
067
067
067
068
068
069
069
069
070
071
071
072
072
073
074
074
074
075
075
075
075
075
075
076
076
076
077
077
077
078
078
078
078
079
079
080
080
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
26
26
26
26
26
26
26
27
27
27
27
27
27
27
27
27
27
27
28
28
28
28
29
29
29
29
29
30
30
30
31
31
31
31
31
31
32
32
32
33
33
33
34
34
34
34
35
35
36
36
CÓDIGO
CIIU 1 DIG
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
180
DESCRIPCIÓN
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
Industrias Manufactureras
CIIU 1 DIG
FILA
PRODUCTO
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
220
221
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
COLUMNA
ACTIVIDAD
081
082
083
084
085
085
086
086
086
086
086
086
086
086
086
086
086
087
088
089
090
091
089
090
092
093
094
095
095
096
096
096
096
096
096
097
098
098
099
099
100
101
101
101
101
101
101
102
103
104
105
105
MATRIZ CUADRADA
CÓDIGO
CIIU 2 DIG
37
40
40
41
45
45
45
45
45
45
45
45
45
45
45
45
45
45
45
50
50
50
51
52
52
55
55
60
60
60
60
60
60
60
60
60
61
61
62
62
63
63
63
63
63
63
63
63
63
64
64
64
CÓDIGO
CIIU 1 DIG
D
E
E
E
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
G
G
G
G
G
G
H
H
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
181
DESCRIPCIÓN
CIIU 1 DIG
Industrias Manufactureras
Suministro de Electricidad, gas y agua
Suministro de Electricidad, gas y agua
Suministro de Electricidad, gas y agua
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Construccion
Comercio
Comercio
Comercio
Comercio
Comercio
Comercio
Hoteles y restaurantes
Hoteles y restaurantes
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
Transporte, Almacenamiento y comunicaciones
FILA
PRODUCTO
251
252
253
254
255
256
257
258
259
260
261
262
263
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
COLUMNA
ACTIVIDAD
105
105
105
106
106
107
107
107
108
108
108
109
109
109
110
110
111
111
112
113
114
114
115
116
117
118
118
118
118
118
119
120
121
121
121
122
122
122
123
124
124
125
125
125
125
126
126
126
127
MATRIZ CUADRADA
CODIGO
CIIU 2 DIG
64
64
64
65
65
65
65
65
66
66
66
67
67
67
67
67
70
70
70
70
71
71
71
72
73
74
74
74
74
74
75
75
80
80
80
85
85
85
90
91
91
92
92
92
92
93
93
93
95
CODIGO
CIIU 1 DIG
I
I
I
J
J
J
J
J
J
J
J
J
J
J
J
J
K
K
K
K
K
K
K
K
K
K
K
K
K
K
L
L
M
M
M
N
N
N
O
O
O
O
O
O
O
O
O
O
P
182
DESCRIPCIÓN
CIIU 1 DIG
Transporte, almacenamiento y comunicaciones
Transporte, almacenamiento y comunicaciones
Transporte, almacenamiento y comunicaciones
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Intermediación financiera
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Actividades inmobiliarias, empresariales y de alquiler
Administracion Pública y Defensa
Administracion Pública y Defensa
Enseñanza
Enseñanza
Enseñanza
Servicios Sociales y de Salud
Servicios Sociales y de Salud
Servicios Sociales y de Salud
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Otras actividades
Hogares Privados con Servicios doméstico
Cuadro 4
Agregación final de las matrices Insumo-Producto cuadradas
13 x 13 a nivel de un de la CIIU
CÓDIGO
CIIU 1 DIG
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
AGREGACIÓN INSUMO PRODUCTO 13 x 13
CÓDIGO
CIIU
DESCRIPCIÓN
CIIU 1 DIG (13 x 13)
1 DIG
Agricultura, ganadería, caza y silvicultura
A
Agricultura, ganadería, caza y silvicultura
Pesca
B
Pesca
Explotación de minas y canteras
C
Explotación de minas y canteras
Industrias manufactureras
D
Industrias manufactureras
Suministro de electricidad, gas y agua
E
Suministro de electricidad, gas y agua
Construcción
F
Construcción
Comercio
G
Comercio
Hoteles y restaurantes
H
Hoteles y restaurantes
Transporte, almacenamiento y comunicaciones
I
Transporte, almacenamiento y comunicaciones
Intermediación financiera
J
Intermediacion financiera
Actividades inmobiliarias, empresariales y de alquiler
K
Actividades inmobiliarias, empresariales y de alquiler
Administracion pública y defensa
L
Administracion pública y defensa / enseñanza / salud
Enseñanza
L
Administracion pública y defensa / enseñanza / salud
Servicios sociales y de salud
L
Administracion pública y defensa / enseñanza / salud
Otras actividades
O
Otras actividades
Hogares privados con servicios doméstico
O
Otras actividades
Organizaciones y órganos extraterritoriales
O
Otras actividades
DESCRIPCIÓN
CIIU 1 DIG
183
BIBLIOGRAFÍA
ALLEN, R. (1997). Multi-Sector Simulation Model of Soviet Economics
Development. Department of Economics, University of British
Columbia, Vancouver, B.C. V6T 1Z1, Canada.
AMAYA, A. (1995). Modelo Insumo-Producto de Leontief. Trabajo especial de grado presentado ante la Universidad de Los Andes para
optar al título de licenciada en Matemática. Mérida.
AMBLER, S., E. CARDIA Y C. ZIMMERMANN (2000). International
Transmission of the Business Cycle in a Multi-Sector Model,
Department de Sciences Economics, Montreal University, Canadá.
ANTONELLI, E. Y M. LORENTE (1997). Insumo-Producto y Comercio Exterior: Un análisis provincial. Instituto de Investigaciones Económicas-Consejo de Investigación (Universidad Nacional de Salta),
Buenos Aires.
ASCÚA, R. (2002). Devaluación, matriz Insumo-Producto e impacto en
la economía de la región. El caso de la industria láctea en Santa Fe.
Centro de Estudios Fundación Potenciar, www.fundacionpotenciar.org.ar.
BACHARACH, M. (1970). Biproportional Matrixes and Input-Output
Change, Cambridge, Cambridge University Press.
BALL F., Y P. DE SASTRE (2002). Multiplicador turístico, este trabajo
fue desarrollado en el marco del PI N° 436 según Disposición SCT
Nº 109 de la Universidad Nacional de la Patagonia, San Juan Bosco,
Facultad de Ciencias Económicas sede Trelew.
BANCO CENTRAL DE CHILE (1996). Matriz Insumo-Producto de la economía chilena, autor, Chile.
184
BANCO CENTRAL DE LA REPÚBLICA ARGENTINA (BCRA) (1997). Comprendiendo la utilidad de la Matriz de Insumo-Producto (MIP),
Argentina.
BANCO MUNDIAL (1995). World Tables, Ed. World Bank.
BAUMOL, W. (2000). “What Marshall didn’t know: On the Twentieth
Century’s Contributions to Economics”, The Quarterly Journal of
Economics, febrero 2000, Vol. CXV, N° 1.
BERLIANT, M., Y S. DAKHLIA (1997). Sensitivity Analysis for Applied
General Equilibrium Models in the Presence of Multiple
Equilibrium. Department of Economics, Washington University,
Campus Box, 1208, 1 Brookings Drive, St. Louis, MO, 631304899, USA.
BONET, J. (2000). La Matriz Insumo-Producto del Caribe Colombiano.
Banco de la República, Cartagena de Indias, Centro de Estudios
Económicos Regionales, N° 15, Mayo, 2000.
BOYD, R. Y M. IBARRARÁN (1996). Integración de Modelos de Energía.
Proyecto Economía-Energía-Medio Ambiente. Universidad de
Ohio-Departamento de Economía. Universidad de las AméricasPuebla. Departamento de Economía. [email protected].
BRAINARD, W Y H. SCARF (2000). How to compute equilibrium prices
in 1891, Yale University.
BULMER -T HOMAS (1982). Input-Output Analysis in Developing
Countries. Sources, Methods and Applications. John Wiley & Sons,
LTD. New York.
BULMER-THOMAS, V. (1982). Input-Output Analysis in Developing
Countries. NewYork: John Wiley & Sons, Ltd.
BUSETTO, F. (2001). The Subjective Approach to General Equilibrium
Under Imperfect Competition. Università di Udine, Dipartimento
di Scienze Economiche, via Tomadini, 30, 33100, Udine, Italy.
185
CAÑADA, M. (1997). Introducción práctica a la contabilidad nacional y
el marco Input-Output: Un manual asistido por ordenador (Adaptado al SEC-95). INE y Colección Libros de autor, Madrid.
CARDENETE, A. Y F. SANCHO (*) (2002). An Applied General Equilibrium
Model to Assess the Impact of National Tax Changes on a Regional Economy. Documento de Trabajo, Serie Economía, E2002/13,
Fundación Centro de Estudios Andaluces.
CARDENETE, A. Y F. SANCHO (**) (2004). El Marco del SEC 95 y las
Matrices de Contabilidad Social. Documento de Trabajo, Serie
Economía, E2004/03, Fundación Centro de Estudios Andaluces.
CARDONA, M. (2001). Relaciones productivas y configuración de la
política sectorial en el Valle de Aburrá. Economía, Sociedad y Territorio, Vol. III, N° 10, 2001, 261-290. Universidad EAFIT, Colombia.
CHIANG, A. (1987). Métodos Fundamentales de Economía Matemática. Mc Graw Hill, México.
CHIAPPORI, P., I. EKELAND; F. KÜBLER Y H. M. POLEMARCHAKIS (2002).
Testable implications of general equilibrium theory: a differentiable
approach. Working Paper, N° 02-10, Department of Economics,
Brown University.
CÍSCAR, J. (1998). Quantification of the Socioeconomic Effects of
Renewable Energy Technologies in Southern Mediterranean
Countries: an Input-Output Evaluation. Institute for Prospective
Technological Studies (IPTS) European Commission
CLEMENTE , L., R. F ARIS Y A. P UENTE (2002). Natural Resource
Dependence, Volatility and Economic Performance in Venezuela:
the Role of a Stabilization Fund. Working Papers: Andean
Competitiveness Project.
186
CLEMENTE, L. A. PUENTE (1989). La matriz de Insumo-Producto para
Venezuela (1981-1984), un instrumento de política económica. Revista BCV, (abril-mayo-junio), Caracas.
CORTÉS, M. Y RÓMULO PINZÓN. (2001). Bases de Contabilidad Nacional, según el SCN, 1993. Departamento Administrativo Nacional
de Estadística (DANE). 3ª Edición, Colombia.
DE CASTRO, J. Y J. TUGORES (1991). Fundamentos de Microeconomía.
Segunda Edición. Mc Graw Hill, México.
DE TARSO, P. (2002). Generación de empleo: Análisis de los efectos de
cambios tecnológicos a partir de un estudio de caso. Revista Espacios, Vol. 23, N° 2, Brasil.
DIRVEN, M. (2002). Los encadenamientos de la agricultura chilena,
acercamiento a una medición. Unidad de Desarrollo Agrícola,
Cepal.
ELÍAS, S. Y M. FERNÁNDEZ (2000). “La Composición Sectorial de la
Producción: Un Análisis Comparativo para América Latina”. Departamento de Economía. Universidad Nacional del Sur, Bahía
Blanca, Argentina, agosto, 2000.
FARMER, K. Y R. WENDNER (2001). Dynamic Multi-Sector CGE
Modeling and the Specification of Capital. Department of
Economics, Graz University, Universitaetsstrasse 15, RESOWIF4, A-8010, Graz, Austria.
FERNÁNDEZ, E. (1994). Análisis Insumo-Producto como instrumento
de planificación para una economía en desarrollo. Trabajo especial de grado presentado ante la Universidad Central de Venezuela
para optar al título de Economista, Caracas.
FMI, OCDE, NACIONES UNIDAS (1993). Sistema de Cuentas Nacionales. Publicaciones Naciones Unidas, Nueva York.
187
FUENTES, N. Y SASTRE M. (2001). Evaluación de la congruencia entre
Economía y Gobierno en torno al desarrollo regional de Baja
California Sur, México. Problemas del Desarrollo, Vol. 32, N° 126,
IIEc-UNAM, julio, septiembre, 200, México.
GARCÍA Y AMO SAUS (2000). Modelo Input-Output de Leontief: Teoría
de Grafos frente a estructuras Pretopológicas. Departamento de
Economía y Empresa Universidad de Castilla-La Mancha, España
GARCÍA, A. Y C. RAMOS (*). (2002) Análisis del cambio estructural a
partir de un método de extracción. Departamento de Economía
Aplicada, Universidad de Oviedo, España.
GARCÍA, A. Y C. RAMOS (**). (2003). Las redes sociales como herramienta de análisis estructural Input-Output. REDES. Revista hispana para el análisis de redes sociales. Vol. 4, N° 5, Jun-Jul. http:/
/revista-redes.rediris.es
GUO, J. Y M. A. PLANTING (2000). Using Input-Output Analysis to
Measure U.S. Economic Structural Change Over a 24 Year Period.
Industry Economics Division, Bureau of Economic Analysis, U.S.
Department of Commerce, Washington, D.C. 20230.
GUZMÁN, J. (1999). Análisis de un modelo dinámico sectorial. UNAM.
http://www.hemerodigital.unam.mx/ANUIES/unam7problems/113/
sec_7.html.
HAJI, J. A. (1987). Linkages, Key Sectors and the Structure of Production
in Kuwait. An Input-Output Approach. Publicado en: Applied
Economics, Volume 19, pages, 1187-1200.
HAMMOND, P. (1995) Mathematics for Economics Analysis. Edit.
Prentice Hall, México.
HEDI, M. Y DECREUX; J. L. GUÉRIN Y S. JEAN (2002). Mirage, a Computable General Equilibrium Model for Trade Policy Analysis, CEPII,
Working Paper, N° 2002-17.
188
HENDERSON & QUANDT. (1981). Teoría Microeconómica. Edit. Ariel,
Barcelona, España.
INSTITUTO NACIONAL DE ESTADÍSTICA E INFORMÁTICA DE PERÚ (2001).
Multiplicadores de la Economía Peruana. Una aplicación de la Tabla
Insumo-Producto de 1994. Colección: Cambio de Año Base de las
Cuentas Nacionales del Perú. Año Base, 1994, N° 6.
INSTITUTO NACIONAL DE ESTADÍSTICA Y CENSOS DE ARGENTINA (INEC).
(2001). Matriz Insumo-Producto Argentina, 1997. Las publicaciones editadas por el Instituto Nacional de Estadística y Censos
INDEC, Centro Estadístico de Servicios, Julio A. Roca, 615, P.B.,
C.P. (1067), Buenos Aires, Argentina.
INSTITUTO NACIONAL DE ESTADÍSTICAS DE ESPAÑA (INE). (1995). Nota
metodológica sobre la tabla simétrica de la economía española para
1995, España.
IVEPLAN (1993). Modelos Macroeconómicos y Matrices Insumo-Producto. Planificación y Política, Publicaciones Iveplan, N° 7.
JENSEN, B. Y M. LARSEN (2004). General Equilibrium Dynamics of MultiSector Growth Models. Presented at the NUS Research Seminar.
Singapore, March, 25.
JOHNSON, P. Y N. ISLAM (2003). Agricultural Processing and the Wa
Economy: A General Equilibrium Analysis. Paper from: Research
Papers: Economic Services Group and Regional Economists Ross
Kingwell (ed.) Miscellaneous Publication (Department of
Agriculture, Western Australia).
JONES, H. (1988). Introducción a las Teorías Modernas del Crecimiento Económico. Segunda Edición. Edit. Antoni Bosch. España.
KEHOE, T. (1996). Social Accounting Matrixes and Applied General
Equilibrium Models. Federal Reserve Bank of Minneapolis.
Research Department.
189
KING, R. G. Y REBELO, S. (1990). “Public policy and economic growth:
developing neoclassical implications”, Journal of Political
Economy.
KOHLI, M. (2001). The Leontief-BLS partnership: a new framework
for measurement. Monthly Labor Review, June, 2001. Labor
Statistics, New York.
KURZ, H. Y SALVADORI, N. (1998). The Dynamic Leontief Model and
the Theory of Endogenous Growth. A paper to be presented at the
Twelfth International Conference on Input-Output Techniques, New
York.
LAGUNA, C. (2003). El modelo de Insumo-Producto. Aplicación básica
y extensiones. Instituto Politécnico Nacional. Centro de Investigaciones Socioeconómicas. Universidad Tecnológica de México.
LAVOIE, C., M. MÉRETTE Y M. SOUISSI (2001). A Multi-Sector MultiCountry Dynamic General Equilibrium Model with Imperfect
Competition. Department of Finance, Working Paper, Economic
Studies and Policy Analysis Division, Economic and Fiscal Policy
Branch.
LEONG, K. (2002). A dynamic computable general equilibrium (CGE)
model of the New Zealand economy. New Zealand Treasury,
Working Paper, 02/07, Wellington, New Zealand.
LEONTIEF, W. (1987). “Input-Output analysis”, The New Palgrave. A
Dictionary of Economics, vol. 2.
LEONTIEF, W. (1966). Input-Output Economics, Oxford University Press.
LIEW, C. (2001). The Dynamic Variable Input-Output Model: An
Advancement from the Leontief Dynamic Input-Output Model.
Annals of Regional Science, Vol. 34, N° 4, January, 2001,
University of Central Oklahoma.
190
LOFGREN, H., R. LEE Y S. ROBINSON (2002). A Standard Computable
General Equilibrium (CGE) Model in GAMS. International Food
Policy Research Institute, Washington, D.C.
LONG, J. Y C. PLOSSER (1983). Real Business Cycles. Journal of Political
Economy. Vol. 91, N° 1.
MARIÑA, A .(1995). Componentes del cambio en la capacidad sectorial
de creación e inducción de empleo: un enfoque de Insumo-Producto. Dep. de Economía de la Univ. Metropolitana. Unidad de
Azcapotzalco. México. http://www.azc.uam.mx/publicaciones/etp/
num7/a6.htm.
MARTÍNEZ, C., G. MORALES Y R. VALDEZ (2001). Cambios estructurales
en la demanda por trabajo en Chile. Vol. 4, Nº 2 / agosto, 2001.
MCGILVRAY, J. (1977). Linkages, Key Sectors and Development strategy.
Publicado en: Structure, System and Economic Policy. Editado por
W. Leontief. Cambridge University Press.
MILLER, R.E. Y BLAIR, P.D. (1985). Input-Output Analysis, Foundations
and Extensions, Prentice-Hall Inc., (Eaglewood Cliffs, New Jersey).
MUN-HENG, T. (1995). Projecting the Leontief inverse directly by the
RAS method. National University of Singapore. Paper prepared
for presentation at the 12th International Conference on InputOutput Techniques, New York, 18-22, May, 1998.
NACIONES UNIDAS (1990). Clasificación Industrial Internacional Uniforme de todas las Actividades Económicas, Oficina de Estadística, Informes Estadísticos, Serie M, Nº 4, Rev. 3, Nueva York.
NACIONES UNIDAS (1995). Problemas y Análisis de las Tablas de InsumoProducto, Oficina de Estadística, Estudios de Métodos, Serie F,
Nº 14, Rev.1, Nueva York.
191
NACIONES UNIDAS (2000). Manual sobre la compilación y el análisis de
los cuadros Insumo-Producto. Autor, Nueva York.
NICHOLSON, W. (1998). Teoría Microeconómica. Sexta Edición. Edit.
Mc Graw Hill. Buenos Aires.
OKUYAMA, Y. M. SONIS Y G. HEWINGS (2002). Structural Change of the
Chicago Economy: A Temporal Inverse Analysis. Research Paper,
2002-10. Paper presented at the 14th International Conference on
Input-Output Techniques, October, 10-15, 2002, Montreal, Canada.
PAVÍA, B. Y CABRER. J. (2003). Flujos demográficos regionales: un análisis Input-Output. Estadística Española, Vol. 45, N° 154, 2003,
págs. 407 a 429.
PETERSON, W. (1991). Advances in Input-Output Analysis: Technology,
Planning and Development, Oxford University Press.
POLO, C. Y E. VALLE (2002). Un análisis Input-Output de la economía
balear. Estadística Española, Vol. 44, N° 151, págs. 393 a 444.
PREM S. L. (1975). Linkages, Key Sectors in some Underdeveloped
Countries. Publicado en: Kyklos, Volume 28, Number 1, pág. 72-79.
PUENTES, R. (1993). Modelos de Determinación del Producto, el Empleo y Precios. Una Aplicación del modelo Insumo- Producto al
Caso Venezolano. Trabajo Especial de Grado para optar al título
de Economista. Venezuela, Caracas, UCV.
QUAN KIU, A. (2001). Nuevos enfoques de utilización de la Matriz de
Insumo-Producto, aportes: Revista de la Facultad de EconomíaBUAP. Año VII, N° 19.
REVISTA BCV (1989). Publicaciones Banco Central de Venezuela. Volumen 4, Abril-Mayo-Junio.
ROZENOV, R. (1998). Use of Input-Output tables in the Analisis of
Structural Changes: The Case of Bulgaria. Center for Economic
192
Reform and Transformation. Heriot-Watt University, Riccarton,
Edinburgh.
SÁEZ, F. (1992). Estudio del Modelo Insumo-Producto a través de la
utilización de tecnologías no lineales (incorporación de las funciones de producción neoclásicas al esquema industrial). Trabajo especial de grado presentado ante la Universidad Central de Venezuela para optar al título de Economista. Caracas.
SECRETARÍA DE AGRICULTURA, GANADERÍA, PESCA Y ALIMENTOS DE
ARGENTINA (2002). Contabilidad Social del Sector Agroalimentario
(MCSSA): Apertura y construcción de la primera versión. Dirección Nacional de Mercados Agroalimentarios, Argentina.
SHOVEN, J. Y J. WHALLEY (1992). Applied General Equilibrium Analysis.
Cambridge: Cambridge University Press.
SONIS, M. Y HEWINGS, G. (2000). Introduction to Input-Output Structural
Q-Analysis. REAL 00-T-1. Web page: www.uiuc.edu/unit/real.
STEWART, G. W. (1973). Introduction to Matrix Computations. Academic
Press, New York.
TAKAHASHI, H. (2003). Optimal Balanced Growth in a General Multisector Endogenous Growth Model with Constant Returns. The
paper was presented at the conference “Irregular Growth: Beyond
Balanced Growth” held on June, 19-21, 2003 in Paris. I had useful
comments from the participants, especially Gerhart Sorger at
London University.
TAKAYAMA, A. (1994). Mathematical Economics. 2ª edición. Cambridge
University Press.
VARGA, R. (1962). Matrix Iterative Analysis, Prentice- Hall, New Jersey.
VARIAN, H. (1998). Microeconomía Intermedia. Cuarta Edición. Edit.
Antoni Bosch. España.
193
VILLAR, A. (1999). Lecciones de Microeconomía. Edit. Antoni Bosch.
España.
WEST, G. Y R. BROWN (2003). Structural Change, Intersectorial Linkages
and Hollowing-Out in the Taiwanese Economy, 1976-1994. School
of Economics. The University of Queensland, Brisbane, 4072. Australia. February, 2003.
WORD, R. J. Y M. J. O’NEILL. (2001). Estimating the Condition Number
of a Leontief System. School of Information Technology, Charles
Sturt University, Bathurst, N.S.W. 2795, Australia.
ZAKARIAS, G., O. FRITZ; W. POINTNER Y M. STEINER (2001). An InputOutput analysis of regional clusters. Paper to be presented at the
Annual Meeting of the Austrian Economic Association, 2001,
(NOeG 2001), Graz, May 17-18.
ZALAI, E. (1998). Computable General Equilibrium Modeling and
Application to Economies in Transition, Centre for Economic
Reform and Transformation, Department of Economics, HeriotWatt University, Riccarton, Edinburgh. http://www.hw.ac.uk/
ecoWWW/cert/certhp.htm.
194