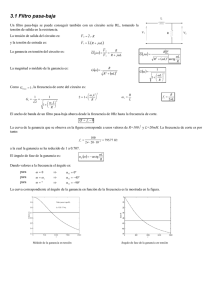
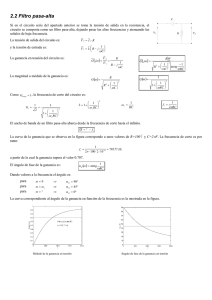
Filtro pasa
Anuncio

4.1 Filtro pasa-banda Tomando como tensión de salida V 2 , la tensión en la resistencia del circuito serie RLC de la figura, esta es: L C V 2 = I1 ⋅ R y la tensión de entrada es: 1 V 1 = I 1 ⋅ R + j ωL − ωC La ganancia en tensión es: G ( jω ) = V2 G ( jω ) = La magnitud o módulo de la ganancia es: G (ω ) = V1 V1 R V2 R 1 R + j ωL − ωC = R 0º 1 2 ωL − 1 ωC R 2 + ωL − arctg R ωC G (ω ) = R 1 R 2 + ωL − ω C 2 1 1 ωL 1+ − R ωRC 2 Dando valores crecientes a la frecuencia a partir de 0Hz se obtiene la curva de ganancia del circuito. Se observa que para la frecuencia de 0Hz y para valores elevados, la ganancia se anula, es decir, se atenúan considerablemente las frecuencias bajas y altas. Sin embargo existe un punto máximo en la curva que corresponde a la frecuencia de resonancia del circuito. A esta frecuencia la tensión de entrada V 1 y la intensidad I 1 están en fase, es decir, se anulan las impedancias reactivas del circuito. ω rL = 1 ω rC ωr = 1 LC fr = 1 2π LC De la curva se puede deducir que existen dos puntos para Gc = Como GVmax = 1 : 1= 1 = Gc = 2 1 ωcL ω 2 RLC − R − = c ω c RC ω c R 2C R 1 2 , es decir, hay dos frecuencias de corte fc1 y fc2 . ω L 1 2 = 1+ c − ω c RC R 1 ω L 1 1+ c − ω c RC R 2 ω 2c RLC − ω c R 2C − R = 0 ω 2c − 1 R =0 ωc − L LC Esta ecuación de segundo grado tiene dos soluciones para ωc y por tanto para fc: ωc 1 = R 1 − 2L 2 4 R2 R 1 + =− + 2L 2 L2 LC ωc 2 = R 1 + 2L 2 4 R2 R 1 + = + 2L 2 L2 LC 4 R2 + L2 LC f c1 = − 4 R2 + L2 LC f c2 = El ancho de banda del filtro es: 1 R + 4πL 4π 1 R + 4πL 4π ∆f = f c 2 − f c1 = 4 R2 + L2 LC 4 R2 + L2 LC R 2πL La curva de la ganancia que se observa en la figura corresponde a unos valores de R=100Ω, L=20mH y C=2 µF. La frecuencia de resonancia es por tanto: fr = 1 2π ⋅ 20 ⋅ 10 − 3 ⋅ 2 ⋅ 10 − 6 La frecuencia de corte inferior es: . Hz f c1 = 49182 La frecuencia de corte superior es: f c2 = 1287.59 Hz El ancho de banda del filtro es: ∆f = 100 = 795.77 Hz 2π ⋅ 20 ⋅ 10− 3 Entre las frecuencias de corte la ganancia supera el valor 0.707. El ángulo de fase de la ganancia es: Dando valores a la frecuencia el ángulo es: = 795.77 Hz ωL 1 α G (ω ) = arctg − R ωRC 2 para para para para para ω=0 ⇒ α G = 90º ω = ω c1 ⇒ α G = 45º ω = ωr ⇒ α G = 0º ω = ω c2 ⇒ α G = −45º ω=∞ ⇒ α G = −90º La curva correspondiente al ángulo de la ganancia en función de la frecuencia es la mostrada en la figura. Módulo de la ganancia en tensión Ángulo de fase de la ganancia en tensión