Estática: Taller 2 – Momentos y sistemas equivalentes de fuerzas

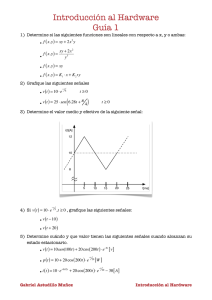
Estática: Taller 2 – Momentos y sistemas equivalentes de fuerzas.
TALLER 2: MOMENTOS Y SISTEMAS EQUIVALENTES DE FUERZAS.
Solucione los siguientes ejercicios pensando, antes de resolver cada uno, los pasos necesarios para
solucionarlo y las ecuaciones a utilizar.
Cualquier inquietud enviarla a [email protected] o personalmente en horario de consulta.
Pasos para elaborar un diagrama de cuerpo libre. (Según Bedford y Fowler)
1. Identificar el cuerpo por aislar: La elección suele estar dictada por las fuerzas particulares que
se quieren determinar.
2. Dibujar un croquis del cuerpo aislado de su entorno y mostrar las dimensiones y ángulos
pertinentes.
3. Dibujar los vectores que representen todas las fuerzas externas que actúen sobre el cuerpo
aislado y designarlas apropiadamente.
2.
La biela AB ejerce sobre la manivela
BC una fuerza de 2.5 kN dirigida hacia abajo y
hacia el lado izquierdo a lo largo de la línea
central de AB. Determine el momento de esa
fuerza respecto a C. Respuesta: +140 N · m.
1.
Un atleta se está ejercitando mientras
carga en el tobillo, A, un pequeño peso de 5 lb,
como indica la figura. Determine a) el momento
del peso respecto a la flexión de la rodilla en el
punto B, b) la magnitud de la fuerza P muscular
que forma un momento de igual magnitud
respecto a B, c) la fuerza F mínima aplicada en
C que crea el mismo momento que el peso
respecto a B.
Respuestas: a) MB = 67.6 lb · pul, b) P = 21.21
lb, c) F = 3.76 lb.
3.
Un pequeño bote cuelga de dos grúas,
una de las cuales se muestra en la figura. La
tensión en la línea ABAD es de 369 N.
Determine el momento respecto a C, de la
fuerza resultante RA ejercida sobre la grúa en el
punto A. Respuesta: 886 N x m i + 259 N x m j
-670 N x m k
Estática: Taller 2 – Momentos y sistemas equivalentes de fuerzas.
Conociendo que la línea central de la llave es
paralela al eje x, determine el momento de la
fuerza sobre A.
4.
La magnitud de la fuerza vertical W es
160 N. Los cosenos directores del vector
posición de A a B son cos θx= 0.500, cos θy
=0.866, cos θz = 0, y los cosenos directores del
vector posición de B a C son: cos θx= 0.707,
cos θy =0.619, cos θz = -0.342. El punto G es el
punto medio de la línea de B a C. Determine el
vector rAG X W, donde rAG es el vector
posición de A a G. Respuesta: -16.44 i + 0 j81.95 k (Nxm)
5.
Se aplica una fuerza de 8 lb a la llave
para apretar el tubo de la ducha AB.
6.
Antes de que el tronco del árbol caiga,
los cables AB y BC son atados como se
muestra. Conociendo que la tensión en los
cables AB y BC son 777 N y 990 N
respectivamente, determine el momento sobre
O de la fuerza resultante ejercida sobre el árbol,
por los cables en B. Respuesta: 5.24 kN x m i –
3.75 kN x m k.
Determine además la distancia del punto O al
cable AB Respuesta. D= 5.49 m.