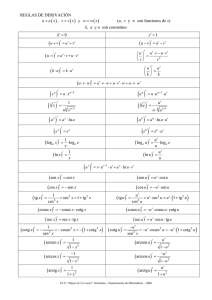
` ` f fry fy ∙ ∙ = =

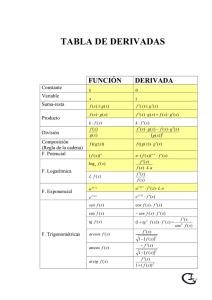
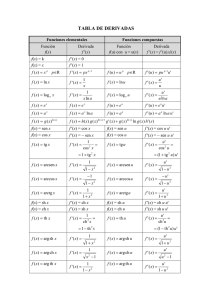
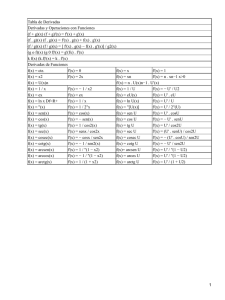
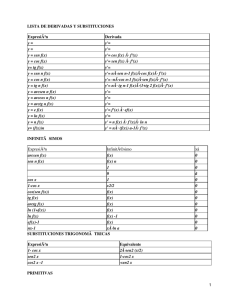
Tabla de derivadas
y  f ( x )  g ( x)
y  f [ g ( x )]
y  f g
f
4) Cociente de funciones
y
g
5) Casos particulares con constantes (k):
f
a) y  k  f
y'  k  f '
b) y 
k
y '  f ' ( x)  g ' ( x )
y '  f '[ g ( x)]  g ' ( x)
y'  f ' g  g ' f
f ' g  g' f
y' 
g2
1) Linealidad de la derivada
2) Regla de la cadena
3) Producto de funciones
r
6) Potencias: y  f
7) Casos particulares (raíces)
a) y 
f
y '
y' 
f'
k
c) y 
k
f
y'  
y '  r  f r 1  f '
f'
2 f
b)
yr f
y' 
f'
r r f r 1
8) Exponenciales:
a) y  e f
y'  e f  f '
b) y  a f
y '  a f  f ' ln a
9) Logarítmicas:
a) y  ln f
y
f'
f
b) y  log a f
9) Trigonométricas:
a) y  sen f
b) y  cos f
c) y  tg f
d) y  cot g f
e) y  arcsen f
f) y  arccos f
g) y  arctg f
k f'
f2
y ' f ' cos f
y '   f ' senf
f'
y' 
 (1  tg 2 f )  f '
cos 2 f
f'
y'  
sen 2 f
f'
y' 
1 f 2
f'
y'  
1 f 2
f'
y' 
1 f 2
y' 
f'
f'
log a e 
f
ln a  f