af′ TABLAS DE DERIVADAS kxf = )( 0)( = ′ → xf )( )( = ′ → = kx

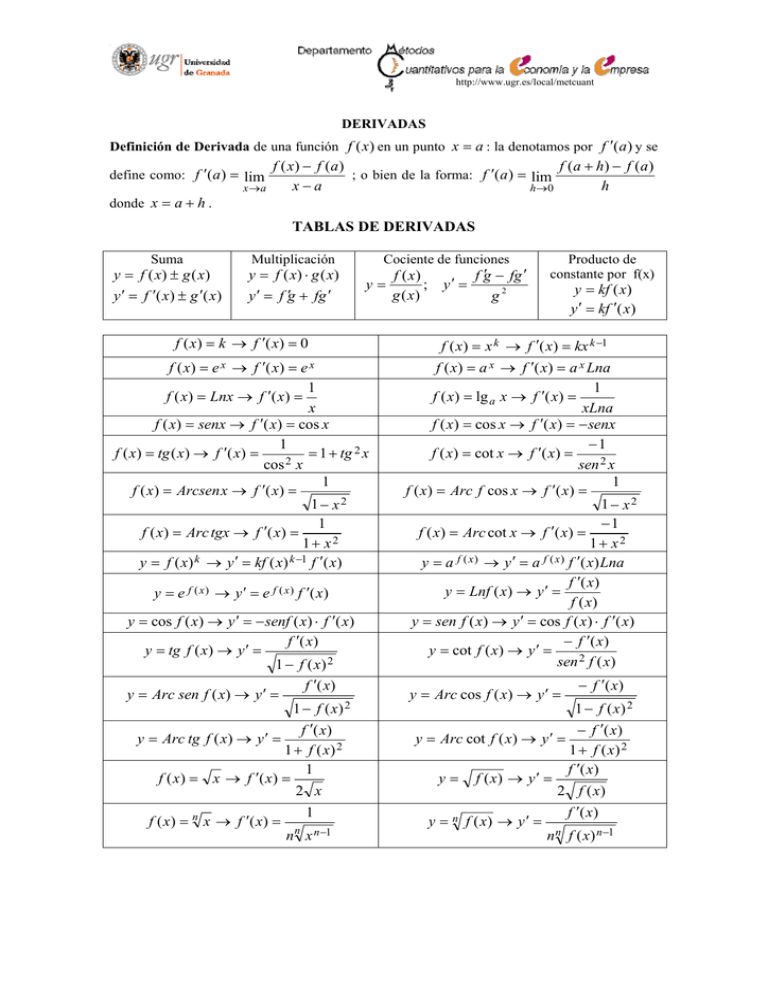
http://www.ugr.es/local/metcuant
DERIVADAS
Definición de Derivada de una función f (x) en un punto x = a : la denotamos por f ′(a ) y se
define como: f ′( a ) = lim
donde x = a + h .
x →a
f ( x) − f (a )
f ( a + h) − f ( a )
; o bien de la forma: f ′( a ) = lim
x−a
h
h →0
TABLAS DE DERIVADAS
Suma
y = f ( x) ± g ( x)
y ′ = f ′( x) ± g ′( x)
Multiplicación
y = f ( x) ⋅ g ( x)
y ′ = f ′g + fg ′
Cociente de funciones
y=
f ( x) = k → f ′( x) = 0
f ( x) = e x → f ′( x) = e x
1
f ( x) = Lnx → f ′( x) =
x
f ( x) = senx → f ′( x) = cos x
1
f ( x) = tg ( x) → f ′( x) =
= 1 + tg 2 x
cos 2 x
1
f ( x) = Arcsen x → f ′( x) =
1− x2
1
f ( x) = Arc tgx → f ′( x) =
1+ x2
y = f ( x) k → y ′ = kf ( x) k −1 f ′( x)
y = e f ( x ) → y ′ = e f ( x ) f ′( x)
y = cos f ( x) → y ′ = − senf ( x) ⋅ f ′( x)
f ′( x)
y = tg f ( x) → y ′ =
1 − f ( x) 2
f ′( x)
y = Arc sen f ( x) → y ′ =
1 − f ( x) 2
f ′( x)
y = Arc tg f ( x) → y ′ =
1 + f ( x) 2
1
f ( x) = x → f ′( x) =
2 x
f ( x) = n x → f ′( x) =
1
n x n −1
n
f ( x)
;
g ( x)
y′ =
f g′ − fg ′
g2
Producto de
constante por f(x)
y = kf (x)
y ′ = kf ′(x)
f ( x) = x k → f ′( x) = kx k −1
f ( x) = a x → f ′( x) = a x Lna
1
f ( x) = lg a x → f ′( x) =
xLna
f ( x) = cos x → f ′( x) = − senx
−1
f ( x) = cot x → f ′( x) =
sen 2 x
1
f ( x) = Arc f cos x → f ′( x) =
1− x2
−1
f ( x) = Arc cot x → f ′( x) =
1+ x2
y = a f ( x ) → y ′ = a f ( x ) f ′( x) Lna
f ′( x)
y = Lnf ( x) → y ′ =
f ( x)
y = sen f ( x) → y ′ = cos f ( x) ⋅ f ′( x)
− f ′( x)
y = cot f ( x) → y ′ =
sen 2 f ( x)
y = Arc cos f ( x) → y ′ =
− f ′( x)
1 − f ( x) 2
− f ′( x)
y = Arc cot f ( x) → y ′ =
1 + f ( x) 2
f ′( x)
y = f ( x) → y ′ =
2 f ( x)
f ′( x)
y = n f ( x) → y ′ =
n n f ( x) n−1
http://www.ugr.es/local/metcuant
EJERCICIOS DE REPASO.
2.- f ( x) = 7 x 4 − 5 x 2 + 9 x
3.- f ( x) = 7 x 2 − 25 x − 4
2
4.- f ( x) = x 3
5.- f ( x) = 5 x 4 − 7 x 3 + 6 x 2 − 7
(
)4
−4
f ( x) = (3x 2 − 4 x + 6)
−
f ( x) = (6 x 2 − 9 x − 7 )
6.- f ( x) = x 2 + x + 1
7.8.-
1
2
9.- f ( x) = Ln(3x)
10.- f ( x) = Ln
x2 +1
x2 − 5
(
3
x
f ′( x) = 28 x 3 − 30 x + 9
f ′( x) = 14 x − 25
2 1
f ′( x) = x − 3
3
f ′( x) = 20 x 3 − 21x 2 + 12 x
f ′( x) =
1.- f ( x) = Lnx 3
)
11.- f ( x) = Ln x 2 + 1
12.- f ( x ) = Ln ( x 2 − x + 5) 3
f ′( x) = 4(x 2 + x + 1) (2 x + 1)
3
f ′( x) = −4(3x 2 − 4 x + 6) (6 x − 4)
1
−3
f ′( x) = − (6 x 2 − 9 x − 7 ) 2 (12 x − 9 )
2
1
f ′( x) =
x
2x
2x
f ′( x) = 2
− 2
x +1 x − 5
2x
f ′( x) = 2
x +1
1
2 − x + 6 )2 (2 x − 1)
(
f ′( x) =
3
x
(x 2 − x + 5)3
−5
2
13.- f ( x) = e x + x +1
f ′( x) = (2 x + 1)e x
2
14.- f ( x) = 25 x + x +1
f ′( x) = 25 x
2 + x +1
2 + x +1
Ln 25(2 x + 1)