NOTACIÓN CIENTÍFICA

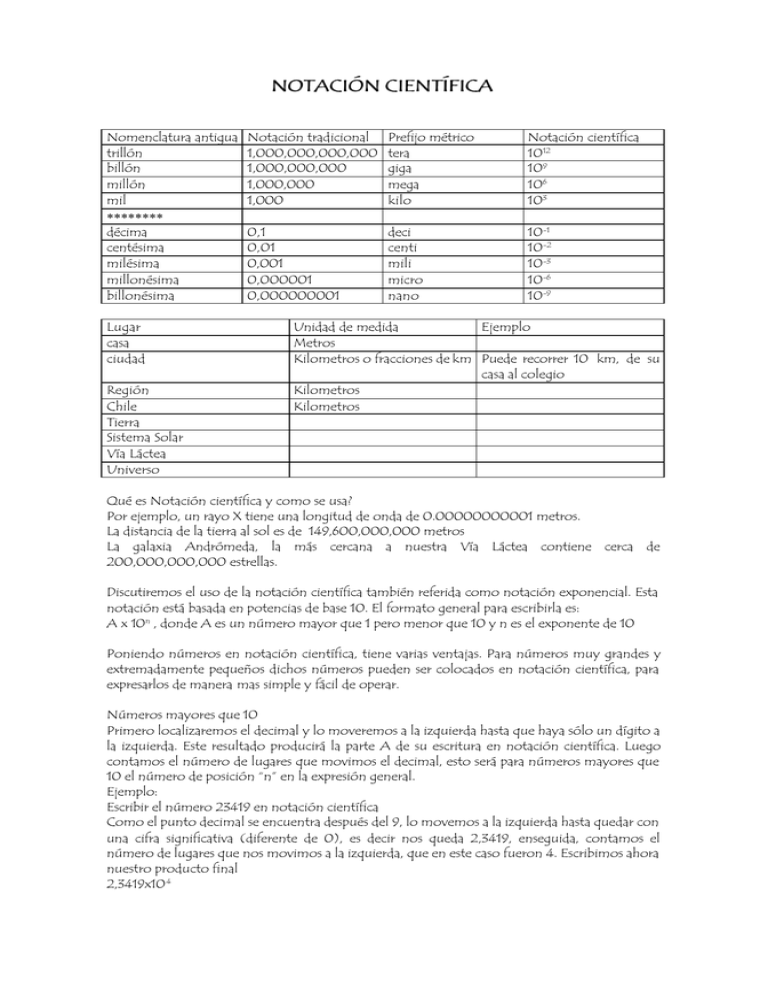
NOTACIÓN CIENTÍFICA
Nomenclatura antigua
trillón
billón
millón
mil
∗∗∗∗∗∗∗∗
décima
centésima
milésima
millonésima
billonésima
Lugar
casa
ciudad
Región
Chile
Tierra
Sistema Solar
Vía Láctea
Universo
Notación tradicional
1,000,000,000,000
1,000,000,000
1,000,000
1,000
Prefijo métrico
tera
giga
mega
kilo
Notación científica
1012
109
106
103
0,1
0,01
0,001
0,000001
0,000000001
deci
centi
mili
micro
nano
10-1
10-2
10-3
10-6
10-9
Unidad de medida
Ejemplo
Metros
Kilometros o fracciones de km Puede recorrer 10 km, de su
casa al colegio
Kilometros
Kilometros
Qué es Notación científica y como se usa?
Por ejemplo, un rayo X tiene una longitud de onda de 0.00000000001 metros.
La distancia de la tierra al sol es de 149,600,000,000 metros
La galaxia Andrómeda, la más cercana a nuestra Vía Láctea contiene cerca de
200,000,000,000 estrellas.
Discutiremos el uso de la notación científica también referida como notación exponencial. Esta
notación está basada en potencias de base 10. El formato general para escribirla es:
A x 10n , donde A es un número mayor que 1 pero menor que 10 y n es el exponente de 10
Poniendo números en notación científica, tiene varias ventajas. Para números muy grandes y
extremadamente pequeños dichos números pueden ser colocados en notación científica, para
expresarlos de manera mas simple y fácil de operar.
Números mayores que 10
Primero localizaremos el decimal y lo moveremos a la izquierda hasta que haya sólo un dígito a
la izquierda. Este resultado producirá la parte A de su escritura en notación científica. Luego
contamos el número de lugares que movimos el decimal, esto será para números mayores que
10 el número de posición “n” en la expresión general.
Ejemplo:
Escribir el número 23419 en notación científica
Como el punto decimal se encuentra después del 9, lo movemos a la izquierda hasta quedar con
una cifra significativa (diferente de 0), es decir nos queda 2,3419, enseguida, contamos el
número de lugares que nos movimos a la izquierda, que en este caso fueron 4. Escribimos ahora
nuestro producto final
2,3419x10 4
Ahora veremos el proceso con números menores que 1
Generalmente se sigue el mismo proceso para la posición decimal con sólo una cifra diferente
de cero y tenemos que movernos a la derecha. La cantidad de cifras que nos movimos a la
derecha será –x , en otras palabras en este caso el exponente es negativo.
Ejemplo: expresar el número 0,000436 en notación científica.
Movemos el decimal a la derecha hasta llegar a la primera cifra significativa en este caso el 4,
por lo tanto nos queda 4,36, luego contamos los lugares que nos movimos que fueron 4, por
lo tanto n=-4. Es decir el número es 4,36 x 10-4
¿Qué ocurre con los números entre 1 y 10?
Estos números no necesitan mover el decimal y su exponente será 0. Por ejemplo:
7,92 puede ser reescrito en notación científica como 7,92 x 100
ejercicios: Expresar en notación científica
a) 123,876.3
b) 1,236,840.
c) 4.22
d) 0.000000000000211
e) 0.000238
f) 9.10
Completar la tabla
medida
Distancia sol - pluton
Distancia tierra – luna
Longitud de onda de onda de
radio
Tamaño de un átomo de
cobre
Tamaño de un rayo gamma
pequeño
Masa del sol
Diámetro de calisto
Diámetro de urano
Longitud de onda de la luz
violeta
Longitud de onda de la luz
roja
Grosor del cabello humano
Forma standard (en metros)
5,913,000,000,000
384,404,000
100,000
Notación científica
0,00000000026
0,000000000000001
70,000,000,000 kilos
5,000,000 metros
50,000,000 metros
0,0000004 metros
0,0000007 metros
0,00001 metros
Veremos ahora como se multiplica en notación científica. El formato general para multiplicar
en notación científica es el siguiente:
(A x 10n) (B x 10m) = (AB)x 10n + m
primero multiplicamos A y B y su resultado se multiplica por 10 elevado a la suma de los
exponentes respectivos.
Por ejemplo
(3 X 104) (1 X 10²)
primero 3 X 1=3
Segundo (104) (10²) = 104+2 = 106
Luego 3 X 106 es la respuesta
Otro ejemplo:
(4 X 103) (2 X 10-4)
primero 4 X 2 = 8
Segundo (103) (10-4) = 10 3-4 = 10-1
Finalmente 8 X 10-1 es la respuesta
Ejercicios
a) (3 X 105 ) (3 X 106) = ?
b) (2 X 107) (3 X 10 -9 ) = ?
c) (4 X 10-6) (4 X 10-4) = ?
es necesario tener en cuenta que todas las respuestas deben quedar expresadas en notación
científica. Es decir hay que observar el resultado y ver si el número que aparece antes de la
potencia de 10 es mayor que 10 o menor que 1.
Por ejemplo
Supongamos que nuestro resultado es 165 x 108
Debemos ajustar su escritura a notación científica. Observamos que debemos mover el decimal
dos lugares a la izquierda, con lo cual sumamos 1 por cada posición que nos movemos. Por lo
tanto en nuestro ejemplo como nos movemos dos lugares a la izquierda debemos sumar 2 al
exponente, quedándonos 1,65x1010
Por otro lado si requerimos mover el decimal a la derecha, entonces debemos restar 1 por cada
posición que nos movamos, por ejemplo.
0.0078 X 105
se requiere que el decimal se mueva 3 posiciones a la derecha, por lo tanto debemos restar 3 al
exponente
7.8 X 105-3 = 7.8 X 10²
Recordemos entonces:
i) para mover el decimal a la izquierda sumamos 1 al exponente por cada posición decimal que
nos movamos.
II) para mover el decimal a la derecha restamos 1 al exponente por cada posición decimal que
nos movamos
División en notación científica
El formato general es el siguiente:
A x 10 n = A x 10n-m
B x 10m B
Ejemplo
6 X 105 =
2 X 10²
dividimos los valores A y B es decir 6/2 = 3
restamos los exponentes, es decir 5 –2 = 3
escribimos el resultado 3 x 10 3
otro ejemplo
8 X 10-3 = 4 x 10-3-(-2) = 4x 10-3+2 = 4x10-1
2 X 10-2
Ejercicios :
Calcule las divisiones:
3.45 X 10 8
6.74 X 10-2
(asegúrese de expresarlo en forma standard)
6.7 X 107
8.6 X 103
4.7 X 10 -2
5.7 X 10 -6
(asegúrese de expresarlo en forma standard)
(asegúrese de expresarlo en forma standard)
Suma y resta usando notación científica
Lo mas importante es que para sumar o restar los exponentes de las potencias de 10 respectivas
deben ser los mismos. El formato general es el siguiente (luego de cerciorarse que los
exponentes sean los mismos)
(A X 10n) + (B X 10n) = (A + B) X 10 n
o
(A X 10n) - (B X 10 n) = (A-B) X 10n
si los exponentes no son los mismos entonces el decimal de uno de ellos debe ser reposicionado
para que ambos exponentes sean iguales. Por ejemplo:
(2.3 X 10-2) + (3.1 X 10-3)
observamos que los dos exponentes no son los mismos, por lo tanto podemos cambiar el –2 a
–3 o el –3 a –2.. cambiemos el –2 a –3
2.3 X 10-2
recordemos que para cada posición a la derecha sumamos –1 al exponente y para cada posición a
la izquierda sumamos 1 al exponente . En este caso, reposicionamos el decimal una posición a la
derecha y obtenemos:
23. X 10-2 +(-1) = 23. X 10 -3
ahora ambos tienen el mismo exponente
(23. X 10-3) + (3.1 X 10-3) = (23. + 3.1) X 10-3 = 26.1 X 10-3 = 2,61x10 -2
otro ejemplo:
(4.2 X 10 4) - (2.7 X 10²) =
Ajustaremos el exponente del segundo número esta vez. Recordemos que es arbitrario cual se
ajusta.
2.7 X 10²
debemos reposicionar dos lugares a la izquierda para que se sumen 2 al exponente con lo que
llegaremos al exponente deseado.
2.7 X 10² llegamos a 0.027 X 102+2 = 0.027 X 104
Ahora efectuamos la operación:
(4.2 X 10 4) - (0.027 X 104) = (4.2 - 0.027) X 104 = 4.173 X 104
ejercicios::
a) (8.41 X 103) + (9.71 X 104) = ?
b) (5.11 X 10²) - (4.2 X 10²) = ?
c) (8.2 X 10²) + (4.0 X 103) = ?
d) (6.3 X 10-2) - (2.1 X 10-1) = ?
Ejercicios adicionales
Exprese los siguientes números en notación científica
123,876.3 = 1.238763 X 105
1,236,840. = 1.23684 X 106
4.22 = 4.22 X 100
0.000000000000211 = 2.11 X 10 -13
0.000238 = 2.38 X 10 -4
9.10 = 9.10 X 10 0
Calcule los productos
(3 X 105 ) (3 X 10 6) = 9 X 10 11
(2 X 107) (3 X 10-9 ) = 6 X 10-2
(4 X 10-6) (4 X 10-4) = 1.6 X 10 -9
calcule los cuocientes
3.45 X 10 8 / 6.74 X 10 -2 = 5.12 X 109
6.7 X 107 / 8.6 X 103 = 7.80 X 103
4.7 X 10 -2 / 5.7 X 10-6 = 8.25 X 10 3
realice las sumas (o restas)
(8.41 X 103) + (9.71 X 10 4) = 10.55 X 10 4 = 1.055 X 105
(5.11 X 10 2) - (4.2 X 102) = .91 X 102 = 9.1 X 101
(8.2 X 102) + (4.0 X 10 3) = 48.2 X 102 = 4.82 X 103
(6.3 X 10-2) - (2.1 X 10 -1)=-14.7 X 10-2 = - 1.47 X 10-1
Datos de interés
1.- el sol tiene un diámetro de 861,000 millas
2.- Una milla es igual a 5280 piés
3.- Un pié son 12 pulgadas
4.- Una pulgada son 2,54 cm.
5.- la distancia promedio de la tierra al sol son 93 millones de millas
6.- Neptuno está a 2,79 trillones de millas
7.- Un año luz son 6 trillones de millas
8.- La estrella más cercana a la tierra es Alpha Centaury que está a 4,2 años luz de la tierra
9.- La distancia del sol al centro de la Vía Láctea es cerca de 30,000 años luz
10.- la vía láctea tiene cerca de 100,000 años luz de ancho
11.- la distancia a la galaxia Andrómeda es cerca de 2,2 x106 año luz
12.- La galaxia conocida más lejana está a 13 billones de años luz.