LA DERIVADA La tasa de cambio promedio de una función y=f(x
Anuncio
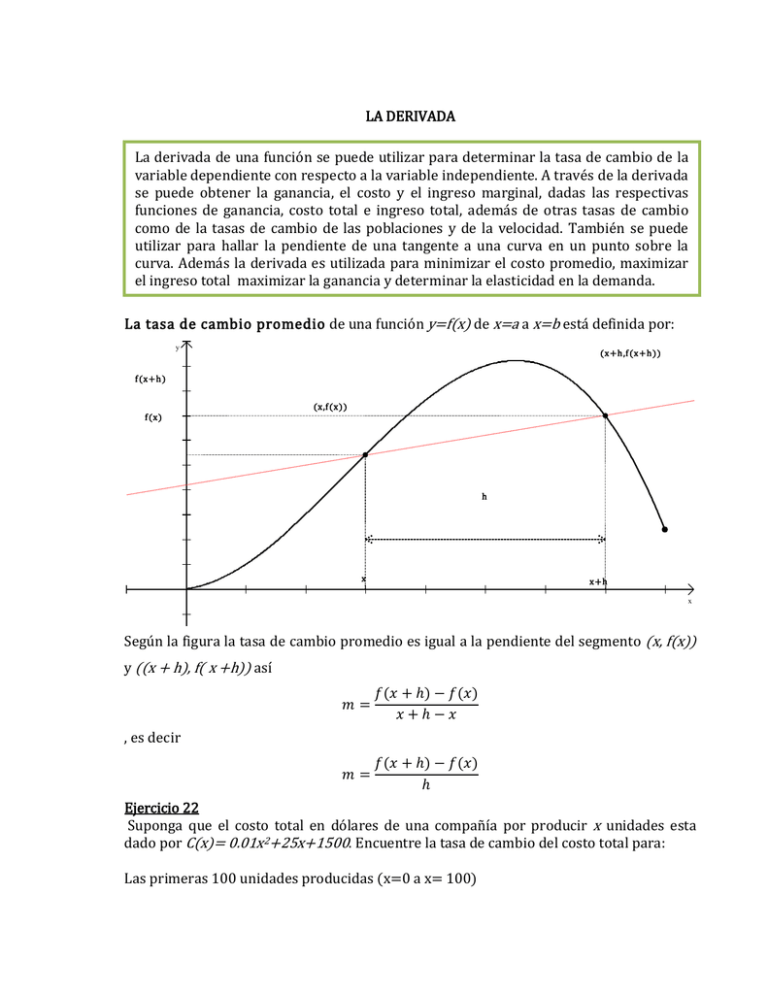
LA DERIVADA La derivada de una función se puede utilizar para determinar la tasa de cambio de la variable dependiente con respecto a la variable independiente. A través de la derivada se puede obtener la ganancia, el costo y el ingreso marginal, dadas las respectivas funciones de ganancia, costo total e ingreso total, además de otras tasas de cambio como de la tasas de cambio de las poblaciones y de la velocidad. También se puede utilizar para hallar la pendiente de una tangente a una curva en un punto sobre la curva. Además la derivada es utilizada para minimizar el costo promedio, maximizar el ingreso total maximizar la ganancia y determinar la elasticidad en la demanda. La tasa de cambio promedio de una función y=f(x) de x=a a x=b está definida por: y (x+h ,f (x+h )) f (x+h ) (x,f (x)) f (x) h x x+h x Según la figura la tasa de cambio promedio es igual a la pendiente del segmento (x, f(x)) y ((x + h), f( x +h)) así , es decir Ejercicio 22 Suponga que el costo total en dólares de una compañía por producir x unidades esta dado por C(x)= 0.01x2+25x+1500. Encuentre la tasa de cambio del costo total para: Las primeras 100 unidades producidas (x=0 a x= 100) Las segundas 100 unidades producidas Tasa de cambio instantánea Suponga que un objeto que se mueve en línea recta tiene su posición y en un momento x dado por y=f(x). Entonces, la velocidad del objeto en el momento x es: , si este límite existe Ejercicio 23 Suponga que se lanza directamente hacia arriba una pelota de modo que su altura f(x) (en pies) se obtiene mediante la ecuación f(x)=96+64x-16x2 Encuentre la velocidad promedio de x=1 a x=1+h Pendiente de la Tangente A la gráfica y=f(x) en el punto A(x1,f(x1) es Si ese límite existe. ES decir, m=f´(x), la derivada en x=x1. Ejercicio 24 Encuentre la pendiente de y=f(x)=x2 en el punto (2,4) DERIVADA Si f es una función definida por y=f(x), entonces la derivada de f(x) para cualquier valor de x, denotada f`(x), es Si este límite existe. Si f`(c) existe, decimos que f es diferenciable en c. Si y= f(x) la derivada de y con respecto a x se denota y´ o Mis Notas de Clase – Cálculo Diferencial Lic. Esp. José F. Barros Troncoso 2 o o Dxy o Dx[f(x)] Ejercicio 25 Encuentre la derivada de cada función f(x) = 2x f(x) = x2 f(x) = x3+1 f(x) = 3x2-2x+1 Problema 14 La función ingreso total de un producto está dada por R=R(x), donde x es el número de unidades vendidas. Entonces el ingreso marginal para x unidades es: Suponga que el ingreso de una compañía petrolera (en miles de dólares) está dado por Donde x es el número de miles de barriles de petróleo que se venden diariamente. Encuentre la función que da el ingreso marginal para cualquier valor de x. Encuentre el ingreso marginal cuando se venden 20 000 barriles, es decir x=20. Remplazando Como x=20 Si se incrementa la producción en 21 mil barriles el ingreso se incrementa en 60 mil dólares Mis Notas de Clase – Cálculo Diferencial Lic. Esp. José F. Barros Troncoso 3 Fórmulas de la Derivada Si f, g y h son funciones definidas en x y k ЄR Tipo Constante Función Derivada f(x)=k f´(x)=0 Ejemplos Si f(x)=5, f´(x)=0 Si f(x)=-2, f´(x)=0 Múltiplo constante f(x)=kx Potencia f(x)=xn Múltiplo Potencia Suma Multiplicación f´(x)=k Si f(x)=3x, f´(x)=3 Si f(x)=-0.5x, f´(x)=-0.5x f´(x)=nxn-1 y f(x)=kxn f´(x)=k.nxn-1 Si f(x)=x4, f´(x)=4x3 Si f(x)=x-3, f´(x)=-3x-4 Si f(x)=5x4,f´(x)=20x3 Si f(x)=-6x5,f´(x)=-30x4 f(x) = [g(x) ± f´(x)=g´(x) ± h´(x) h(x)] Si f(x)= x3+4x2-3x+2, f´(x)=3x2+8x-3 f(x) [g(x).h(x)] f(x)=(x2+2)(3x-1) = f´(x)=g´(x) ± h´(x) - , - - - f´(x)=2x(3x-1)+(x2+2)3 = 6x2-2x+3x2+6 = 9x2+2x+6 f(x)=x3/2(3x2-x-1) f´(x)= - = Cociente k Cociente , - - - - - - - Ejercicios 26 Derivar cada una de las siguientes funciones f(x) = - 4 f(x) = 0.25 f(x)=21x f(x)= f(x)=x5 f(x)= f(x)=4x3 f(x)= f(x)=(x2+1)2 f(x)=4x2 + 5x + 3 f(x)= 6 – f(x)= f(x)= x-2 + x1/2 (x3- f(x)= 1)(5x2+6x) f(x)= - x f(x)= Problemas 15 1. El costo (en dólares) de producir x unidades de cierto artículo es C(x)=5000 + 10x + 0.05x2. Halle el costo marginal (Es decir la razón de cambio de C con respecto a x, cuando x=100. El costo, en dólares, para producir x pares de jeans es 2. C(x)=200 + 3x + 0.01x2+0.0002x3 a. b. c. d. 3. Encuentre la función costo marginal. Halle C`(100) y explique su significado. ¿Qué pronostica? Calcule C(101) – C(100) Compare los resultados de los encisos b y c. ¿Qué encuentra? La función costo de un artículo es C(x)=84000 + 0.16x – 0.6x2 + 0.003x3 a. Encuentre la función costo marginal. b. Halle C`(100) y explique su significado. ¿Qué pronostica? c. Calcule C(101) – C(100) 2. Compare los resultados de los encisos b y c. ¿Qué encuentra? 4. El costo, en dólares, para producir x pares de jeans es C(x)=920 + 2x – 0.02x2+0.00007x3 a. Encuentre la función costo marginal. b. Halle C`(100) y explique su significado. ¿Qué pronostica? c. Calcule C(101) – C(100) d. Compare los resultados de los encisos b y c. ¿Qué encuentra? Mis Notas de Clase – Cálculo Diferencial Lic. Esp. José F. Barros Troncoso 5 Problemas 16 1. El ingreso total (en dólares) obtenido por la venta de x de libreros es , determine: a. La función ingreso marginal (R´(x)) b. Calculo el ingreso marginal si las ventas se incrementan en 300 unidades 2. El volumen de ventas de un disco fonográfico particular está dado como una función del tiempo t por la fórmula S(t)=10 000 + 2 000t -200t2 , donde t se mide en semanas y S es el número de discos vendidos por semana determine la tasa de cambio cuando a. t=4 y ¿qué significa? b. t=8 y ¿qué significa? c. Compare los resultados ¿qué encuentra? 3. El costo en miles de pesos de la elaboración de x miles de CD en cierta productora de discos, esta dado por C(x)=1 500 - 3x + x3, a. Encuentre la tasa de cambio del costo con respecto a la cantidad. b. Calcule C´(100), ¿qué significa? 4. Suponga que un mayorista espera que su ingreso mensual por la venta de televisores pequeños sea , donde x es el número de unidades vendidas. Encuentre su ingreso marginal e interprételo cuando la cantidad vendida es 300, 500 y 600 5. Suponga que el ingreso de una compañía petrolera (en miles de dólares) está dado por la ecuación R(x) = 100x – x2 , donde x es el número de miles de barriles de petróleo que se venden diariamente. Encuentre el ingreso marginal cuando se vende 20 000 barriles (es decir x=20) 6. Suponga que el fabricante de un producto sabe que dada la demanda de este producto, su ingreso esta dado por R(x) = 1 500x – 0.02x2 c n , donde x es el número de unidades vendidas y R(x) está en dólares. Encuentre el ingreso marginal en x=500, interprete el resultado. 7. La producción semanal de cierto producto es Mis Notas de Clase – Cálculo Diferencial Lic. Esp. José F. Barros Troncoso 6 Q(x)= 200x + 6x2 , donde x es el número d trabajadores en la línea de ensamble. En la actualidad hay 60 trabajadores en la línea. Encuentre Q`(x) y calcule el cambio en la producción ocasionada por la suma de un trabajador, interprete el resultado Mis Notas de Clase – Cálculo Diferencial Lic. Esp. José F. Barros Troncoso 7





