El Plano Cartesiano

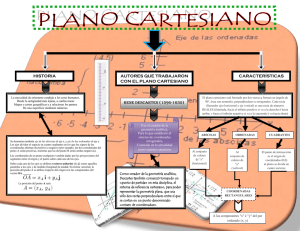
El Plano Cartesiano
RENÉ DESCARTES
Se recuerda sobre todo a este francés extraordinario por su invención de la Geometría Analítica.
Pero su logro más notable fue la reducción de la Naturaleza a leyes matemáticas.
"Consideraría que no sé nada de Física si tan sólo fuese capaz de expresar cómo deben ser las
cosas, pero fuese incapaz de demostrar que no pueden ser de otra manera. No obstante,
habiendo logrado reducir la Física a las Matemáticas, la demostración es entonces posible, y
pienso que puedo realizarla con el reducido alcance de mi conocimiento."
René Descartes
Con estas palabras, René Descartes expresa el pensamiento que lo situaría entre los principales
artífices de la revolución científica del siglo XVII. A las "formas" y las "cualidades" de la Física
Aristotélica, que habían resultado ser un callejón sin salida, contraponía la "idea clara y
fundamental" de que el mundo físico no es más que un puro mecanismo. En Geometría Analítica,
Descartes creó una técnica que le permitía expresar las leyes de la Mecánica , que constituían las
leyes últimas de la Naturaleza, mediante ecuaciones algebraicas. Y entonces propuso el programa
ideal de toda ciencia teórica: construir, con un mínimo número de principios, un sistema que diese
razón de todos los hechos conocidos y que permitiese descubrir hechos nuevos. Toda la Física
Teórica subsiguiente se ha planteado como objetivo la consecución de este ideal. Podemos afirmar
que, en el siglo XVII, Blaise Pascal e Isaac Newton lograron llevar a cabo el programa cartesiano,
que consiste en ofrecer la explicación del mundo físico en función de su mecanismo. (Jimenez,
2011)
No podemos dudar del carácter revolucionario ni de la influencia de las ideas teóricas y del
programa de Descartes. La paradoja es que ésta haya sido tan profunda en personas que
consideraban su enfoque esencialmente inaceptable y que rechazaban algunos de sus
presupuestos fundamentales y de sus conclusiones específicas. Christian Huygens, el gran
matemático y astrónomo holandés, cuyo padre había sido amigo íntimo de Descartes, afirmó a
finales de su vida que sólo podía aceptar una pequeña parte de la Física Cartesiana; pero, al mismo
tiempo, reconocía que había sido la obra Los principios de Filosofía de Descartes, lo que
inicialmente había abierto sus ojos a la ciencia. Él mismo dijo que Descartes no sólo ponía de
manifiesto las limitaciones de la Filosofía de los antiguos , sino que, "en su lugar, ofrece causas
comprensibles de todo lo que existe en la Naturaleza". Como suele ocurrir con frecuencia con las
teorías revolucionarias, el legado de Descartes no fue sólo un logro, sino también una profecía y
una visión.
El propio Descartes se vio obligado a reconocer que su ideal matemático de la ciencia, puramente
deductivo, había fracasado ante las complejidades de la Naturaleza y los enigmas de la materia.
Este fracaso era especialmente evidente en Fisiología, el campo en el que se había aventurado con
mayor osadía. No obstante, de su fracaso y compromiso Descartes extrajo otra contribución para
el pensamiento científico, en muchos aspectos tanto o más importante que el propio programa
teórico. Forzado a recurrir a la experiencia y a las hipótesis, demostró ser el primer gran maestro
del modelo hipotético. Éste se ha convertido en una herramienta esencial en cualquier
investigación científica. En sus modelos teóricos de los procesos fisiológicos, Descartes desplegó
los más ingeniosos ejercicios de su ingenio imaginativo y experimental
EL PLANO CARTESIANO.
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se
cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la
vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen
(Cuéllar, 2008)
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan
por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de
las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano
cartesiano con base en sus coordenadas, lo cual se representa como:
P (x, y)
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha
si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el
cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si
son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus
coordenadas.
Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este procedimiento también se emplea cuando
se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).
De lo anterior se concluye que:
Para determinar las coordenadas de un punto o localizarlo en el plano cartesiano, se encuentran
unidades correspondientes en el eje de las x hacia la derecha o hacia la izquierda y luego las
unidades del eje de las y hacia arriba o hacia abajo, según sean positivas o negativas,
respectivamente.
Doña Lupe nos ha dicho que su farmacia está dentro del centro de la ciudad . Supongamos que
deseamos saber la ubicación exacta de la farmacia de Doña Lupe Una vez que ya estamos en el
centro le preguntamos a un policía para que nos oriente. El policía nos ha dicho que caminemos 5
cuadras hacía el este y 6 cuadras hacía el norte para llegar a la farmacia.La cantidad de cuadras
que tenemos que caminar las podemos entender como coordenadas en un plano cartesiano.
Lo anterior lo podemos expresar en un plano cartesiano de la siguiente manera:
Para el problema planteado , el origen del plano será el punto de partida que es en donde le
preguntamos al policía sobre la ubicación de la farmacia.
.
Bibliografía
Cuéllar, J. A. (2008). Matemáticas 3 Geometría Analítica (Segunda ed.). Méxio D.F.: McGraw Hill.
Jimenez, R. (2011). Matemáticas III Geometría Analítica (Segunda ed.). Estado de México: Pearson.