página 113

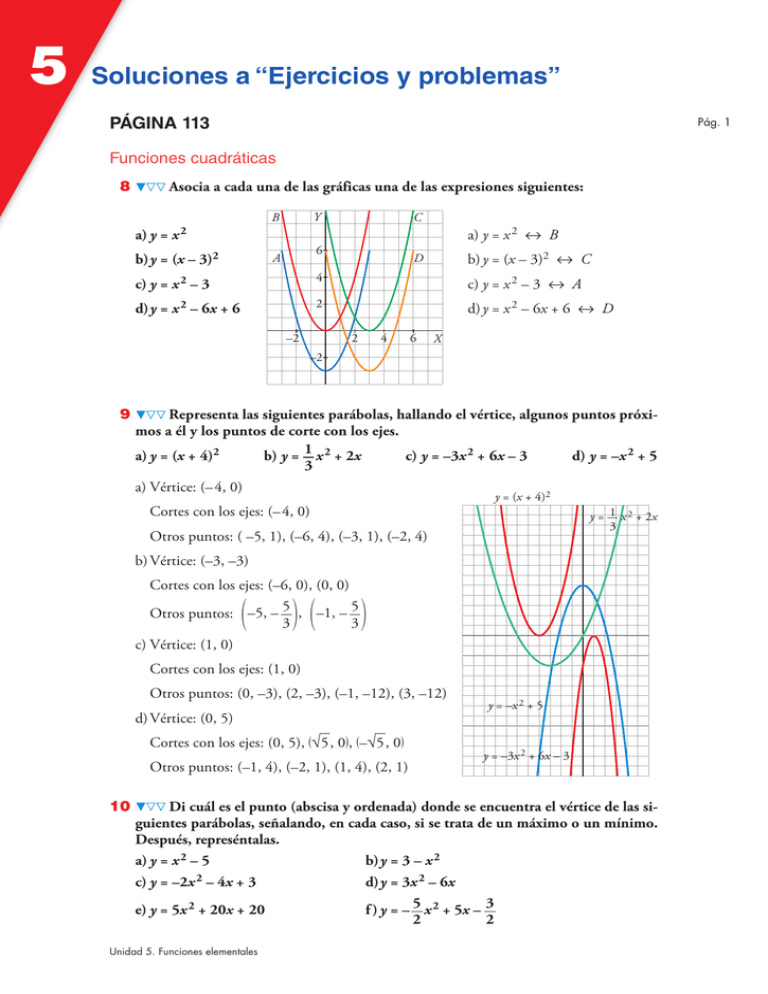
5
Soluciones a “Ejercicios y problemas”
PÁGINA 113
Pág. 1
Funciones cuadráticas
8
Asocia a cada una de las gráficas una de las expresiones siguientes:
a) y =
Y
B
x2
b) y = (x – 3)2
C
6
A
a) y = x 2 5 B
b) y = (x – 3)2 5 C
D
c) y = x 2 – 3
4
c) y = x 2 – 3 5 A
d) y = x 2 – 6x + 6
2
d) y = x 2 – 6x + 6 5 D
–2
2
4
6
X
–2
9
Representa las siguientes parábolas, hallando el vértice, algunos puntos próximos a él y los puntos de corte con los ejes.
b) y = 1 x 2 + 2x
c) y = –3x 2 + 6x – 3
d) y = –x 2 + 5
a) y = (x + 4)2
3
a) Vértice: (–4, 0)
y = (x + 4)2
Cortes con los ejes: (–4, 0)
1 x 2 + 2x
y=—
3
Otros puntos: ( –5, 1), (–6, 4), (–3, 1), (–2, 4)
b) Vértice: (–3, –3)
Cortes con los ejes: (–6, 0), (0, 0)
Otros puntos: –5, – 5 , –1, – 5
3
3
(
) (
)
c) Vértice: (1, 0)
Cortes con los ejes: (1, 0)
Otros puntos: (0, –3), (2, –3), (–1, –12), (3, –12)
d) Vértice: (0, 5)
Cortes con los ejes: (0, 5), (√5, 0), (–√5, 0)
Otros puntos: (–1, 4), (–2, 1), (1, 4), (2, 1)
10
y = –x 2 + 5
y = –3x 2 + 6x – 3
Di cuál es el punto (abscisa y ordenada) donde se encuentra el vértice de las siguientes parábolas, señalando, en cada caso, si se trata de un máximo o un mínimo.
Después, represéntalas.
b) y = 3 – x 2
a) y = x 2 – 5
c) y = –2x 2 – 4x + 3
d) y = 3x 2 – 6x
f ) y = – 5 x 2 + 5x – 3
e) y = 5x 2 + 20x + 20
2
2
Unidad 5. Funciones elementales
5
Soluciones a “Ejercicios y problemas”
–b = 0 = 0 °
§ Vértice en el punto (0, –5).
2a 2
¢
Es un mínimo.
x = 0 8 y = –5 §£
Pág. 2
a) y = x 2 – 5
Y
a) p =
–b = 0 = 0 °
§ Vértice en el punto (0, 3).
2a –2
¢
Es un máximo.
x = 0 8 y = 3 §£
b) p =
X
–b = 4 = –1 °
§ Vértice en el punto (–1, 5).
2a – 4
¢
Es un máximo.
x = –1 8 y = 5 §£
c) p =
b) y = 3 – x 2
–b = 6 = 1 °
§ Vértice en el punto (1, –3).
2a 6
¢
Es un mínimo.
x = 1 8 y = –3 §£
c) y = –2x 2 – 4x + 3
e) y = 5x 2 + 20x + 20
Y
d) p =
–b = –20 = –2 °
§ Vértice en el punto (–2, 0).
2a 10
¢
Es un mínimo.
x = –2 8 y = 0 §£
e) p =
d) y = 3x 2 – 6x
X
–b = –5 = 1 °
§ Vértice en el punto (1, 1).
2a –5
¢
Es un máximo.
x = 1 8 y = 1 §£
f)p =
5 x 2 + 5x – —
3
f) y = –—
2
2
Otras funciones
11
Asocia a cada gráfica la fórmula que le corresponde:
I) y = √x – 3
a)
II) y = √x – 3
b)
Y
2
c)
Y
2
Y
2
2 X
–4 –2
4
6
III) y = 3 – √– x
2
4
d)
X
X
6
Y
2
–2
5
5
5
5
b)
c)
d)
a)
X
–6 –4 –2
12




IV) y = √–3x
Asocia a cada gráfica una de estas fórmulas:
I) y = 1
II) y = 3 – 1
III) y = 2 + 2
2–x
x–3
x
a)
b)
Y
4
Unidad 5. Funciones elementales
Y
4
2
2
–4 –2
IV) y = – 1
x+3
2
4 X
2
4
6 X
5
Soluciones a “Ejercicios y problemas”
c)
X
–4 –2
 5 d)
13
–2
–4
–4
 5 a)
X
4
2
–2
 5 c)
Asocia a cada gráfica una de estas fórmulas. Di, de cada una de ellas, si es creciente o decreciente.
II) y =
1,5 x
III) y = 0,4 x
b
6
I) y = 3 x
c
4
2
2
2
4
–4 –2
 5 d) Creciente.
2
 5 b) Creciente.
4
8
 5 c) Decreciente.
6
6
 5 a) Decreciente.
4
4
2
2
8
–4 –2
6
4
–4 –2
IV) y = 0,7 x
d
2
4
–4 –2
2
4
Representa gráficamente las siguientes funciones:
a) y = √x + 2
b) y = 2 – √x
y = 2 –x
c) y = 2√– x
d) y = –√– x
Y
y= x+2
y=2– x
y = – –x
15
Pág. 3
Y
2
–2
 5 b)
a
14
d)
Y
2
X
Estudia el dominio de definición de las siguientes funciones y represéntalas
gráficamente:
a) y = √2 – x
b) y = 7 – √2x + 4
c) y = √– x
a) Dominio = (– @, 2]
Y
b) Dominio = [–2, + @)
c) Dominio = (– @, 0]
d) Dominio = [–3, + @)
Unidad 5. Funciones elementales
d) y = 2 + √x + 3
y=2+ x+3
y= 2–x
y = –x
y = 7 – 2x + 4
X