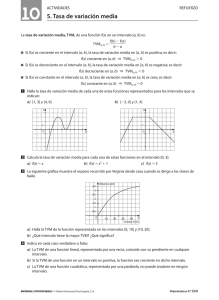
Tasa de variación media

UNL - ATE
Tecnicatura en Administración de Salud - 2011
Módulo Matemática (CLASE 4)
Conceptos importantes:
Tasa de Variación Media: TVM.
Derivada de funciones y = f(x) sencillas.
Recta tangente.
Integrales de funciones y = f(x) sencillas.
Cálculo de áreas.
Tasa de variación media
Se llama tasa de variación media (T.V.M.) en intervalo [x1, x2] de cierta función y
y
= f(x) y se representa por  x , al cociente:
y f ( x2 )  f ( x1 )

x
x2  x1
f ( x2 )  f ( x1 )
TVM 
x2  x1
Interpretación geométrica
La expresión anterior coincide con la pendiente de la recta secante a la
función f(x), que pasa por los puntos P(x1, f(x1)) y Q(x2, f(x2))
1
TVM 
f ( x2 )  f ( x1 )
 msec
x2  x1
Ejemplos:
a) Calcular la T.V.M. de la función f(x) = x2 − x en el intervalo [1,4].
f (4)  f (1) 12  0
TVM 

4
4 1
3
b) El índice de precios al consumidor pasó cierto año de 13,50 a 35,10. Hallar la tasa
de variación media mensual.
35,10  13,50 21,6
TVM 

 1,8
12  0
12
Tasa de variación instantánea. La derivada
Consideremos un valor h (que puede ser positivo o negativo).
La tasa de variación media (TVM) en el intervalo
f ( a  h)  f ( a )
TVM 
aha
, aquí x1 = a y x2 = a+h
[a,
a
+h]
sería
Nos interesa medir la tasa instantánea, es decir el cambio cuando h tiende a cero o
cuando x2 se acerca a x1, es decir:
El valor límite cuando h tiende a cero, si es que se puede determinar es la TASA de
Variación Instantánea de la función y = f(x) cuando x = a. También a ese valor se le
llama la derivada de la función f en el punto a y se designa por f `(a), por lo tanto, la
2
derivada de una función en un punto es el límite de la tasa de variación media cuando el
incremento de la variable tiende a 0.
TVI (cuando x  a)  f `(a)  lim
h 0
f ( a  h)  f ( a )
aha
Si f tiene derivada en el punto a se dice que f es derivable en a.
.
Importante: no necesitamos calcular este límite cada vez que se desea encontrar la TVI
o f `(a), hay reglas para encontrar la derivada de una función conocida la función.
Interpretación geométrica
La expresión anterior coincide con la pendiente de la recta tangente a la función
f(x) en el punto de tangencia P(a, f(a).
La recta tangente a una curva en un punto es aquella que pasa por el punto (a, f(a)) y
cuya pendiente es igual a f '(a), es decir la pendiente es
TVI (cuando x  a)  f `(a)  mtan gente , y la ecuación de la recta tangente está dada
por:
y  f (a)  m( x  a)
O bien
y  f (a)  f ´(a)(x  a)
3
Ejemplo: Hallar la ecuación de la recta tangente a la parábola y = x 2 − 5x + 6 en x =
4.
El punto P(4, f(4)) es decir P(4, 2). También necesitamos m = f ´(2), para ello
derivamos primero:
f ´(x) = 2x – 5
f ´(4) = 2.4 – 5 = 3
Ahora construimos la recta tangente: y – 2 = 3(x -4)
Tabla de derivadas de algunas funciones elementales
1) f(x) =k  f ` (x) =0
2) f(x) = xn  f `(x) = n.x n-1
3) f(x) = ln x  f ´(x) =
4) f(x) = ex  f ´(x) = ex
5) f(x) = sen x  f ´(x) = cos x
6) f(x) = cos x  f ´(x) = -sen x
Si f y g son funciones derivables en a entonces f +g y f.g son derivables en a y se
verifica:
7) (f +g)´(a)= f ´(a) + g´(a)
8) (f.g)´(a) = f´(a).g(a) + g´(a).f(a)
Además si g(a) 0, entonces f/g es derivable en a y se verifica:
9)
4
Ejercicios:
a) Dada la función y = f(x) = x3 + x² + 2x - 1. Hallar la ecuación de las rectas
tangentes en:
a.1) x = 0.
Rta.: y = 2x – 1.
a.2) x = 1.
Rta.: y = 7x – 4.
a.3) x = -1.
Rta.: y = 3x
b) Un móvil lleva un movimiento rectilíneo, cuya relación entre la distancia recorrida
x (en metros) y el tiempo empleado t (en segundos) está dado por: x(t) = 3t² + 2.
b.1) Calcular su velocidad media entre t = 2 y t = 4 segundos. Rta.: 18 m/seg
b.2) Calcular la velocidad instantánea para t = 5 segundos. Rta.: 30 m/seg
Integrales
Recordar que:
Si f(x) = x², entonces f´(x) = 2x.
Si f(x) = x² + 3, entonces f´(x) = 2x.
Si f(x) = x² + 1, entonces f´(x) = 2x.
Si f(x) = x² - 5, entonces f´(x) = 2x.
Así f´(x) = 2x es una función derivada de muchas funciones, todas del tipo f(x) = x²
+ C.
Así se puede escribir lo siguiente:
 2 xdx
= x² + C. Esta integral se llama integral
indefinida.
Así:
 f ( x)dx
= F(x) + C
Se lee : integral de f(x) diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
5
dx es diferencial de x, e indica cuál es la variable de la función que se
integra.
C es la constante de integración y puede tomar cualquier valor numérico
real.
Si F(x) es una primitiva de f(x) se tiene que:
La integral de una suma de funciones es igual a la suma de las integrales de esas
funciones.
 [ f ( x)  g ( x)]dx   f ( x)dx   g ( x)dx
La integral del producto de una constante por una función es igual a la constante
por la integral de la función.
 kf ( x)dx  k  f ( x)dx
También se puede calcular la integral definida:
4
 2xdx
1
=
x²
x4
x 1
= 16 – 1 = 15.
Si en particular la función y = f(x) es no negativa en el intervalo que se desea
calcular la integral definida, el resultado de esa integral definida es el área debajo de
la curva.
6
Un entretenimiento.
Hacemos una excursión en bicicleta a un bosque que está a 45 km. del pueblo. Estamos
allí un rato y volvemos. Para llegar hay que seguir el itinerario con subidas y bajadas
que se bosqueja.
Bosque
Cima
Pozo
Pueblo
ITINERARIO DEL VIAJE
Nos dicen que la gráfica del espacio recorrido en función del tiempo es la siguiente,
donde la variable independiente está medida en horas y la variable dependiente en km.
50
40
30
20
10
0
0
5
10
15
20
Mirando la gráfica espacio o recorrido (en km) contra tiempo (en hora), contestar las
siguientes preguntas:
 ¿A qué hora salimos? ¿A qué hora regresamos?
 ¿Cuántos kilómetros hay, aproximadamente, desde el comienzo de la primera cuesta
hasta la cima? ¿Cuánto tiempo tardamos en subirla?
 ¿Qué distancia hay desde el pozo hasta el bosque? ¿Cuánto tardamos en recorrer
este trayecto?
 ¿Cuánto tiempo descansamos en el bosque?
 Describe el viaje de vuelta.
 ¿Cuánto hemos tardado en ir del pueblo al bosque? ¿Y del bosque al pueblo? ¿A qué
crees que puede deberse la diferencia?
7
 Calcular la velocidad media entre el instante de salida y 5 horas después.
8