ges derivadas lc

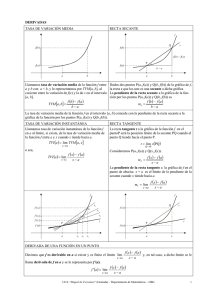
Departamento de Matemáticas.
GES 6.
DERIVADAS
Colegio Maravillas.
El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. Está basado en el
concepto de límite, y tiene variadas aplicaciones. (Se aplica en aquellos casos donde es necesario medir la rapidez con
que se produce el cambio de una magnitud o situación. Es una herramienta de cálculo fundamental en los estudios de Física,
Química y Biología, o en Ciencias Sociales como la Economía y la Sociología).
Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una función no
tiene derivada en sus puntos de discontinuidad, o con tangente vertical o en puntos angulosos.
Introducción geométrica al concepto de derivada.
Supongamos una función f. La derivada de f es otra función que llamaremos f´.
representará la pendiente de la recta tangente a la gráfica de f en el punto a.
Donde f´(a)
Cuando nos referimos a la gráfica en dos dimensiones de f, se considera la derivada como la pendiente
de la recta tangente del gráfico en el punto a. Se puede aproximar la pendiente de esta tangente
como el límite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es
decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden
determinarse muchas propiedades geométricas de las funciones, tales como su crecimiento,
curvatura, etc..
Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento (o decrecimiento)
en un punto a de una función f está dado por f´(a).
En particular, se tiene que la derivada de la función en el punto se define:
Definición 1ª.
si este límite existe, de lo contrario, f' no está definida.
*Definición 2ª. Nosotros utilizaremos esta segunda expresión.
Gráfica de incrementos de la función en x en y
*(El cálculo de la derivada por definición con cualquiera de los límites anteriores
proporciona siempre el mismo resultado).
Conceptos relacionados:
-Tasa de Variación. (TV). La TV de f(x) en un intervalo [a,b] se define como: TV = f(b) – f(a).
Ejemplo: Calcula la TV de f(x) = x2 + 1 en el intervalo [2, 5]. TV= f(5) - f(2) = 26 - 5 = 21.
TV
f (b )  f ( a )
=
ba
ba
f (5)  f ( 2) 26  5 21

 7.
TVM =
=
52
3
3
-Tasa de variación media. (TVM). La TVM de f(x) en [a,b] se define: TVM =
Ejemplo: Calcula la TVM de f(x) = x2 + 1 en [2,5].
-Tasa de variación instantánea. (TVI).
TVI= f´(a) =
Ejemplo: Calcula la TVI de la función f(x) = 3x – 1 en el punto a = 5.
f ( x)  f (5)
3x  1  (14)
3x  15 0
3( x  5)
 lim
 lim
 in det  lim
 3.
TVI = lim
x5
x5
x5
0
x5
x 5
x 5
x 5
x 5
-Ecuación de la recta Tangente a f en un punto a. ERT: y – f(a) = f ´(a)  (x-a).
1
Departamento de Matemáticas.
GES 6.
DERIVADAS
Colegio Maravillas.
Cuando nos piden el cálculo de la derivada de una función, podemos obtenerla mediante su definición, bien
utilizando la expresión de la primera o de la segunda definición, que hemos analizado anteriormente o bien
mediante el estudio de la tabla de las derivadas de las funciones más usuales (Leibniz, Lagrange, Newton,...).
TABLA DERIVADAS de funciones más usuales Nota: a y k son constantes; f, g y h son funciones.
y=a
y=x
y=f±g±h±…
y = k·f
y = f·g
y=
f
g
k
f
f
y=
k
y = xn
y =f n
n
fm f
f   g  f  g
g2
k f
y’ =
f2
f
y’ =
k
y’ = n  xn-1
y’ = n  f n-1  f´
m mn  1
f
f´
y’ =
n
y’ = af  f   ln a
y’ =
y=
y=
y’ = 0
y’ = 1
y’ = f’ ± g’ ± h’ ± …
y’ = k·f’
y’ = f’·g + f·g’
m
n
y = af
y = ef
y = log a f
y = ln f
y = sen f
y = cos f
y = tg f
y = arctg f
y = arcsen f
y = arccos f
y’ = e f  f 
f
loga e
f
f
y’ =
f
y’ =
y’ = cos f · f’
y’ = - sen f· f’
f
cos2 f
f
y’ =
1 f 2
f
y’ =
y’ =
y’ = -
1 f 2
f
1 f 2
2