algebra funciones inversas

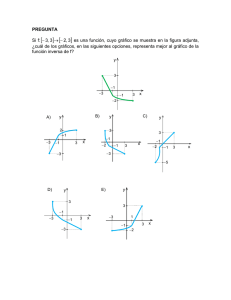
Universidad Tecnológica Centroamericana
Facultad de Ingeniería
Álgebra
Funciones Inversas
Así como existe el criterio de la recta vertical para probar que una gráfica es la gráfica de
una función, también existe el criterio de la recta horizontal y este sirve para verificar que
una función sea uno a uno, es decir, que si se traza una recta horizontal por la grafica de
una función y esta solo la corta en un punto, entonces concluimos que la función es uno a
uno.
¿Cómo determinar que una función tiene inversa?
Si una función es uno a uno entonces tiene inversa de lo contrario no tiene inversa.
Gráficamente: Utilizando el criterio de la recta horizontal.
Algebraicamente: si se cumple que f ( f
concluye que f tiene inversa.
−1
( x)) = x
y
f
−1
( f ( x)) = x entonces se
¿Cómo se encuentra la inversa de una función?
1. Se intercambian las variables (x por y y y por x)
2. Se despeja para y la cual se llamará función inversa f –1
3. Se verifica que la inversa encontrada esté correcta, verificando que al realizar la
compuesta de la función con su inversa y viceversa se cumpla que
f ( f −1 ( x)) = x
y
f −1 ( f ( x)) = x
Vea el ejemplo 5 del libro, pag. 60 y siga los tres pasos escritos arriba.
Características de una función y su inversa.
Sea f una función y f –1 su inversa, entonces se cumple que:
1. El Dominio de f = al Rango de f –1
2. El Rango de f = al Dominio de f – 1
3. La gráfica de f –1 es la gráfica de f reflejada a través de la recta y = x (función
identidad) (Ver la figura 47 a) y b) de la Pág. 59)
4. Los puntos de la función f -1 son los puntos inversos de la función f, es decir que si
la función f tiene los puntos (-2, -1), (-1, 0) y (2, 1) entonces los puntos de f –1 serán
(-1, -2), (0, -1) y (1, 2), nótese que son las mismas coordenadas pero en orden
inverso. (Figura 47 b) Pág. 59)