preparando la prueba estructurada de matemática

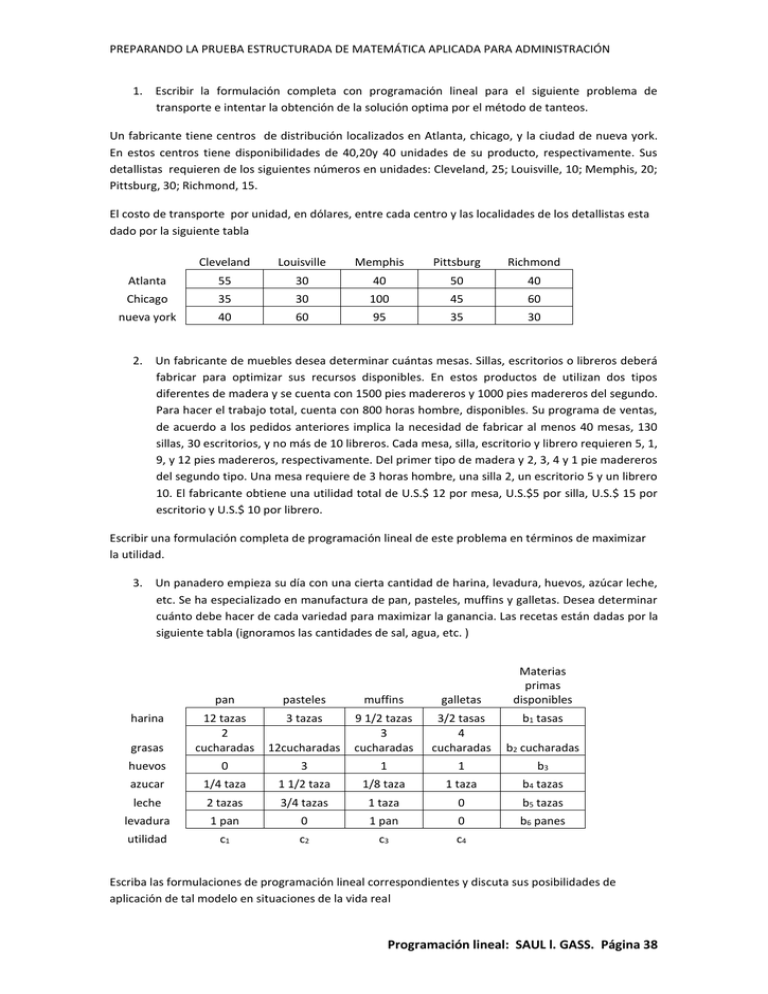
PREPARANDO LA PRUEBA ESTRUCTURADA DE MATEMÁTICA APLICADA PARA ADMINISTRACIÓN
1. Escribir la formulación completa con programación lineal para el siguiente problema de
transporte e intentar la obtención de la solución optima por el método de tanteos.
Un fabricante tiene centros de distribución localizados en Atlanta, chicago, y la ciudad de nueva york.
En estos centros tiene disponibilidades de 40,20y 40 unidades de su producto, respectivamente. Sus
detallistas requieren de los siguientes números en unidades: Cleveland, 25; Louisville, 10; Memphis, 20;
Pittsburg, 30; Richmond, 15.
El costo de transporte por unidad, en dólares, entre cada centro y las localidades de los detallistas esta
dado por la siguiente tabla
Cleveland
Louisville
Memphis
Pittsburg
Richmond
Atlanta
55
30
40
50
40
Chicago
35
30
100
45
60
nueva york
40
60
95
35
30
2. Un fabricante de muebles desea determinar cuántas mesas. Sillas, escritorios o libreros deberá
fabricar para optimizar sus recursos disponibles. En estos productos de utilizan dos tipos
diferentes de madera y se cuenta con 1500 pies madereros y 1000 pies madereros del segundo.
Para hacer el trabajo total, cuenta con 800 horas hombre, disponibles. Su programa de ventas,
de acuerdo a los pedidos anteriores implica la necesidad de fabricar al menos 40 mesas, 130
sillas, 30 escritorios, y no más de 10 libreros. Cada mesa, silla, escritorio y librero requieren 5, 1,
9, y 12 pies madereros, respectivamente. Del primer tipo de madera y 2, 3, 4 y 1 pie madereros
del segundo tipo. Una mesa requiere de 3 horas hombre, una silla 2, un escritorio 5 y un librero
10. El fabricante obtiene una utilidad total de U.S.$ 12 por mesa, U.S.$5 por silla, U.S.$ 15 por
escritorio y U.S.$ 10 por librero.
Escribir una formulación completa de programación lineal de este problema en términos de maximizar
la utilidad.
3. Un panadero empieza su día con una cierta cantidad de harina, levadura, huevos, azúcar leche,
etc. Se ha especializado en manufactura de pan, pasteles, muffins y galletas. Desea determinar
cuánto debe hacer de cada variedad para maximizar la ganancia. Las recetas están dadas por la
siguiente tabla (ignoramos las cantidades de sal, agua, etc. )
harina
grasas
pan
pasteles
muffins
galletas
12 tazas
2
cucharadas
3 tazas
9 1/2 tazas
3
cucharadas
3/2 tasas
4
cucharadas
12cucharadas
Materias
primas
disponibles
b1 tasas
b2 cucharadas
huevos
0
3
1
1
b3
azucar
1/4 taza
1 1/2 taza
1/8 taza
1 taza
b4 tazas
leche
2 tazas
3/4 tazas
1 taza
0
b5 tazas
levadura
1 pan
0
1 pan
0
b6 panes
utilidad
c1
c2
c3
c4
Escriba las formulaciones de programación lineal correspondientes y discuta sus posibilidades de
aplicación de tal modelo en situaciones de la vida real
Programación lineal: SAUL l. GASS. Página 38